基于壓縮感知的MU-MIMO稀疏信道估計

張 婷，周繼華，趙 濤，黃 華

（重慶金美通信有限責任公司，重慶400030）

1 引 言

多徑無線信道上的高速率數據通信通常需要接收機已知信道響應。越來越多的實驗證據表明，許多無線信道都具有稀疏的多徑結構。稀疏多徑結構隨著信號空間維度的變大而更加顯著[1]。多用戶MIMO（Multi-UserMultiple-InputMultiple-Output,MU-MIMO）系統下行信道估計時，隨著天線數量的增加，導頻開銷隨之增加，信道估計的復雜度不斷提高。信道估計的準確程度對信道均衡、解調和信道譯碼，以及接收端的分集合并、相關檢測等操作均有直接影響[2]。

壓縮感知，也稱為壓縮采樣或稀疏采樣。若信號投影到某個域，可被該域內的基表示，那么用較少的信號測量值就能以高概率恢復原始信號[3]。如果信號能被某個基精確表示，并且系數集合x 中k僅僅有s 個系數不為零，就稱為稀疏信號[4]，即在該變換域中，信號的稀疏表示可以被壓縮[5]。

傳統的LS 和MMSE 信道估計算法均需要大量的導頻信號才能做出準確的信道估計。若在稀疏信道下采用傳統的信道估計算法，會造成嚴重的資源浪費[6]。文獻[7-12]研究了多徑稀疏的概念，并提出了基于壓縮感知（Compressed Sensing）理論的估計稀疏多徑（有效地稀疏）信道新方法。與傳統基于LS訓練方法相比，壓縮信道感知只需更少的導頻資源去估計稀疏信道，與基于最小均方誤差的傳統訓練方法相比，能夠利用更少的能量、更低的延遲和帶寬實現目標重構誤差。

針對信道的稀疏特性，將壓縮感知技術應用到MU-MIMO 下行鏈路信道估計，可有效地降低MUMIMO 下行鏈路的導頻開銷，并采用小波域去噪[13]處理，低信噪比條件下也能獲得最優的信道估計性能，實現對信道狀態信息的更優估計，更好地應用于下一代通信系統。

2 壓縮感知

考慮長度為N 的信號f，若其在基底Ψ 上僅有K 個向量有意義，其余都是零（或實際中近似零的，也看作是零），則 f 可由 Ψ 稀疏表示[14]，K 表示信號的稀疏度，有如下式：

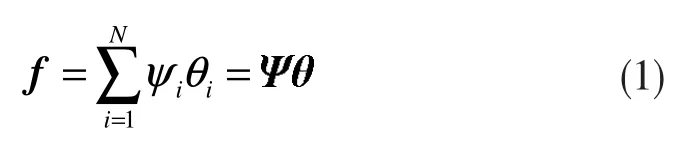
式中，Ψ= ［Ψ1, Ψ2, ..., ΨN］稱為一個基或者框架。θ=［θ1, θ2, ..., θN］稱為稀疏向量。將f 投影到一個M×N（M＜＜N）的觀測矩陣 Φ 中來感知信號，結合(1)式，得到測量向量yf：

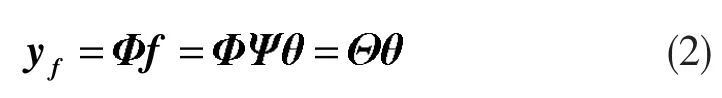
如(2)式所示，矩陣Φ 的每一行產生一個測量值，Θ 為傳感矩陣。由于M＜＜N，即觀測維數M 遠小于信號維數N，當Θ 滿足信號稀疏性和等距約束性（Restricted Isometry Property, RIP），且 RIP 系數 δk滿足時[15]，(2)式所示的重構問題就轉化為1-范數（l1范數）最優化求解，求使l1范數最小化的稀疏解θ，如下式：

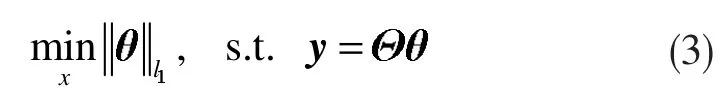
使用壓縮感知重構算法，僅需遠小于N 的M 個測量值就可重構稀疏信號通過f=Ψθ 恢復出原始信號

3 系統模型

考慮MU-MIMO 下行信道鏈路，基站同時為U個用戶發送數據，基站配置NT根發射天線，每個用戶配置Ni根天線[16]，總的接收天線為基站發射的導頻符號表示為x∈CM×1。發射端的并行數據流包括用戶調制符號數據和導頻符號。發端數據經過調制、預編碼后送入信道，接收端對信道進行壓縮測量，得到測量向量，i=1,2, ...,U，采用壓縮感知貪婪重構算法對測量矢量進行重構，恢復出信道響應，實現稀疏信道估計。MU-MIMO 下行稀疏信道估計結構如圖1 所示。

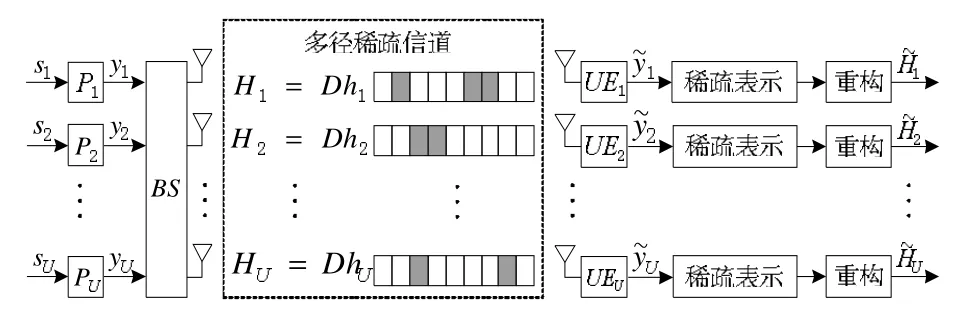
圖1 MU-MIMO 下行稀疏信道估計

系統采用塊對角化的下行傳輸方式，即采用預編碼矩陣P 消除用戶間干擾和信道間干擾，則每個用戶的信道為MU-MIMO 轉換到SU-MIMO 的等價信道Heqii，那么第i 個用戶的等價接收的導頻信號yi∈CNi 可表示為：

上式中信道Heqii的沖激響應是K 稀疏的，xi=［x1, x2, ..., xM］∈CM×1表示基站向第 i 個用戶發送的導頻符號。假設OFDM 調制由N 個子載波構成，L個子載波為導頻符號。利用MIMO 信道矩陣在傅里葉變換基上的稀疏特性[17]，基于壓縮感知的多用戶MIMO 下行信道估計問題可如下式所示[18]：

式中，y 為測量向量，即用戶端接收的導頻符號矩陣；X 為測量矩陣，即收發雙方已知的導頻符號；H=Fh 為信道頻域響應，F 是稀疏矩陣，即根據導頻位置選取的快速傅里葉變換抽取矩陣，h 是H 在基F 下的稀疏表示；令A =XF 需滿足測量矩陣X 與稀疏矩陣F 互不相關。根據(3)式重構出使l1范數最小化的稀疏解，如下式所示：

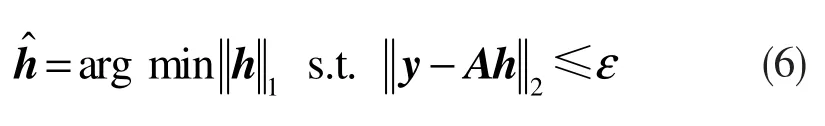
最后，根據H =Fh，恢復出信道狀態矩陣H。

4 稀疏信道估計

在基于壓縮感知的信道估計中，經過塊對角化處理后，每個用戶的等價信道估計通過(3)式所示的最小化1-范數得到。因此，對于一個K 稀疏的信道haT,aR，測量矩陣取決于導頻子載波的位置，以單用戶單接收天線為例，接收機接收的導頻符號y 表示為：

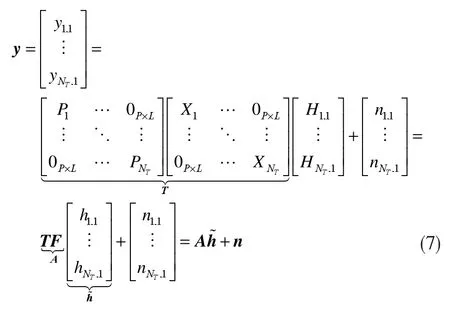
如(7)式所示，稀疏信道估計本質上是在噪聲未知的情況下，充分利用h 的稀疏性，由已知的y 和A來估計h。噪聲影響信號重構性能，接收端的壓縮測量對噪聲也進行了M 到N 維的降維處理（M＜＜N），噪聲同時也被加強，噪聲的放大降低解調性能，同時也降低了信號的稀疏性。采用小波軟閾值去噪對含噪的接收信號進行去噪處理，對去噪后的測量向量進行稀疏信道估計。基于小波閾值去噪的正交匹配追蹤算法（WD-OMP）[19]稀疏信道估計算法流程歸納如下：

1) 初始化：r0=y，索引集 I0=，支撐集 Λ0=，字典矩陣A，稀疏度K，迭代計數t=1；

2) 采用 mallat 算法[20]對r0的高頻分量進行軟閾值去噪，得到降噪的測量信號；

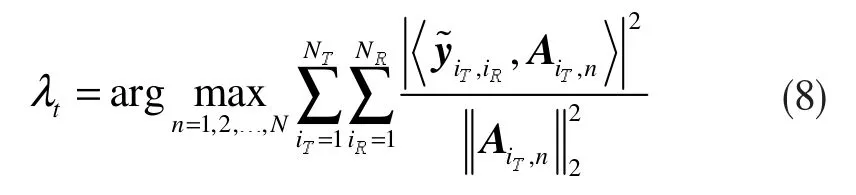
4) 將最大列向量的列標λt加入到索引集It-1，更新矩陣索引集It=It-1∪{λt}；更新支撐集Λ0=［Λt-1,Aλt］，為索引 λt對應的列組成的矩陣；

5 仿真分析

考慮圖1 所示的MU-MIMO 下行鏈路，采用基于塊對角化傳輸策略。將基站側天線配置為NT=6，用戶數為3，每個用戶天線數Ni=2。系統子載波個數為2048，導頻數p1=128，稀疏信道估計采用的導頻數假設系統是同步的，并且不存在多徑能量泄露情況，也不存在多用戶間的干擾。

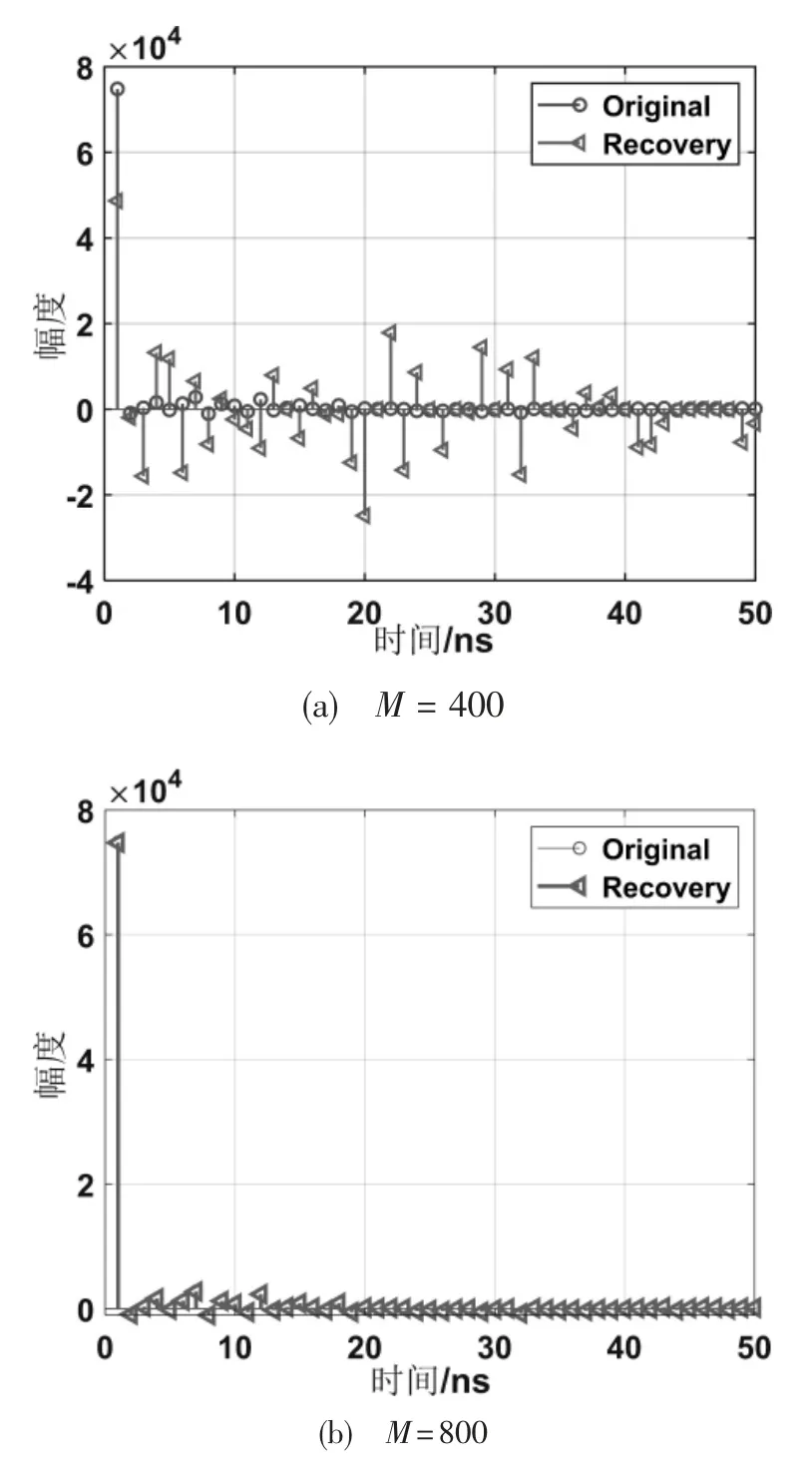
圖2 不同測量數下的重構誤差

選擇高斯白噪聲矩陣作為測量矩陣，采樣點數即測量矩陣的維數M，采用OMP 算法重構稀疏信號。如圖2(a)所示，當測量矩陣維數M 為400 時，原始信號與重構信號誤差較大；如圖2(b)所示，當測量矩陣維數M 為800 時，幾乎能完全重構原始信號。觀測向量的個數影響重構性能，隨著觀測向量（即采用點數）的增多，重構誤差逐漸減少。將壓縮感知理論引入MIMO 稀疏信道估計，其估計性能的優劣與測量矩陣的維數相關。測量向量的數據量越大，則接收端獲得的信道信息就越多，重構誤差就越小，稀疏估計的精度就越高。

圖3 仿真了高斯信道下，LS 算法、OMP 算法、小波域去噪的WD-OMP 算法的BER 性能。如圖所示，在測量向量數相同的情況下，由于濾除了噪聲的影響，WD-OMP 比OMP 在低信噪比下的誤碼率性能更好；由于信道具備稀疏性，基于壓縮感知的稀疏信道估計，在減少導頻數10%的情況下，獲得與LS相同估計精度的同時，稀疏信道估計比傳統的LS信道估計所用的導頻數更少；隨機測量矩陣在測量過程中放大了噪聲，所以在較低信噪比環境下，應用CS 理論估計信道時傳統OMP 算法重構誤差增大。降噪的OMP 算法在避免對噪聲進行放大的同時，也更好地抑制了噪聲，從而得到更好的誤碼率性能。

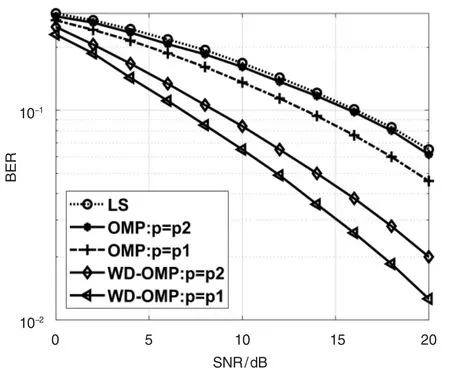
圖3 不同信道估計算法BER 性能比較

6 結束語

MU-MIMO 系統中，在高頻譜利用率情況下對快時變信道進行準確估計是一項挑戰。噪聲影響信號重構性能，針對MU-MIMO 系統的信道估計性能在低信噪比情況下性能差的問題，對接收信道進行小波域去噪處理，利用信道的稀疏性，將稀疏信道估計問題轉化為重構稀疏信號問題，同時在減少導頻開銷的同時提高信道估計性能。基于壓縮感知的信道估計不受Nyquist 采樣條件約束，適用于大規模MIMO、超寬帶通信系統，可利用較少的參考信號達到與傳統信道估計方法等效的信道估計性能，從而提高系統頻譜利用率。