最小二乘法在地質測量中的應用

吳小偉

（西安石油大學地球科學與工程學院，西安710065）

1 引 言

礦區的地質測量工作為礦區的前期規劃和實際開采提供有力的數據支撐。目前常見的GPS 測量技術、數字攝影測量技術等被廣泛應用于礦區的地質測量工作中。此類技術可結合具體地形地貌來計算開采空間、開采時間、開采設備等，也可通過數字影像測出坍塌區的具體形態和特征，如體積、深度、形態等[1-3]。由于地形地貌差異和數據儀器測量精度的影響，會存在一定的誤差[4]，以較大誤差值預測實際的礦產量、開采率等數值，將對生產實踐造成不利影響。最小二乘法作為最佳的觀測組合工具之一[5]，具有精確性高、誤差小的特點，廣泛應用于諸多領域中。在現階段大數據迅猛發展的環境下，以相同地形、地理條件為基準，可對開采礦區的數據進行精準記錄和分析。采用最小二乘法算法，把開采數據隨深度的改變，以體積為參考對實際開采量數據進行建模。根據最小二乘法令平方和最小化的方式減小誤差，通過相關系數，利用MATLAB 軟件編程擬合成具體的函數。后期在具體的評估和預測中，可以從相同的地形和地理位置下從數據庫中匹配曲線函數，計算新礦區的開采量和固定體積開采率等數值。

2 算法應用原理

最小二乘法是高斯于1809 年所著的《天體運動論》中提出的。它是數學中用于數據匹配的一種最佳方法[6]，運用逼近原則，尋求數據，讓實測數據與估計數據平方和最小，即距離和最小，來尋測和匹配最佳的函數數據，從而擬合成函數曲線。

2.1 算法應用的必要性

礦區第一深度空間定義為由地表到深度500m處；第二深度空間為500m～2000m；第三深度空間為2000m 以下[7]。以具體深度空間為界限，對每一深度空間的礦區開采數據進行收集、整理、分析。由于地形地貌的不同，隨著深度的增加，體積的變化，開采總量整體呈上升趨勢。同一定義空間下，由于地表平面的不規則形狀，選取固定深度會造成體積的差異，從而造成固定體積中開采率的差異，所以開采總量的改變不能用具體的函數表示。統計體積V 和開采總量F，用散點圖標記，利用最小二乘法算法，對散點圖采取擬合方式，建模構造函數曲線。同時，針對地形地貌的改變，平面圖形的建立也可采用最小二乘法算法減小誤差，進行建模，模擬函數曲線。

2.2 最小二乘法原理

在對地表平面面積的運算中，長度和寬度的改變，以及礦產資源中固定體積V 與礦產量F 的改變，皆符合建模構造函數曲線。結合擬合次數的方法[8-9]，對散點圖進行數值分析，并通過MATLAB 軟件數據建模，尋求最佳的函數圖像。理論推導過程為：對給定數(xi,yi) （i=0,1,2,...,m），共 m+1 個數據坐標點，選取多項式P(x)，滿足：

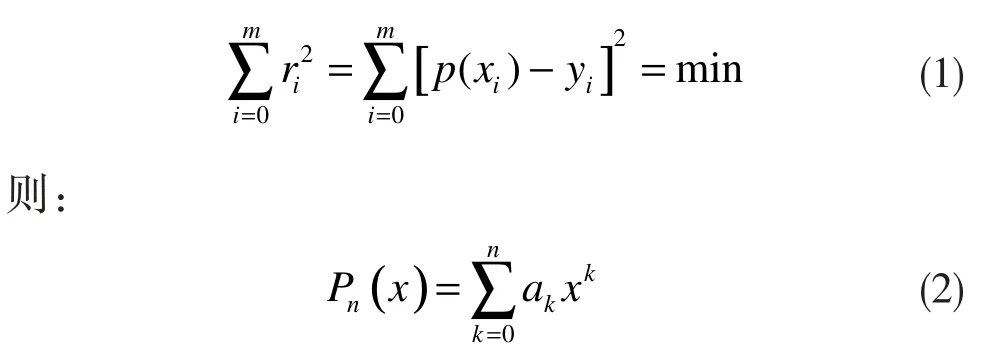
函數P(x)即稱為擬合函數，或最小二乘法解，設：

式中，a0,a1,a2,...,an為待求的未知數，n 為多項式的最高次冪，因此該問題化為求I=I(a0,a1,a2,...,an)的極值問題。由多元函數求極值的必要條件：

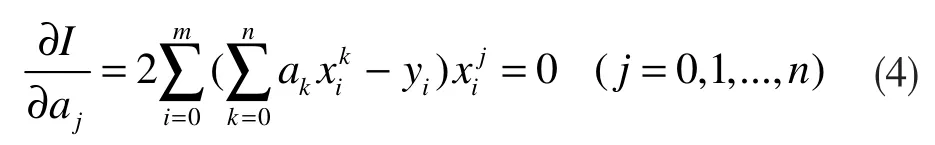
可以得到：

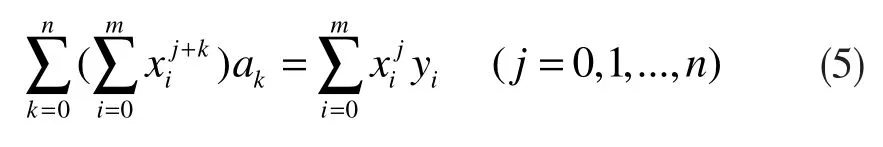
這是一個關于a0,a1,a2,...,an的線性方程組，用矩陣表示如下：

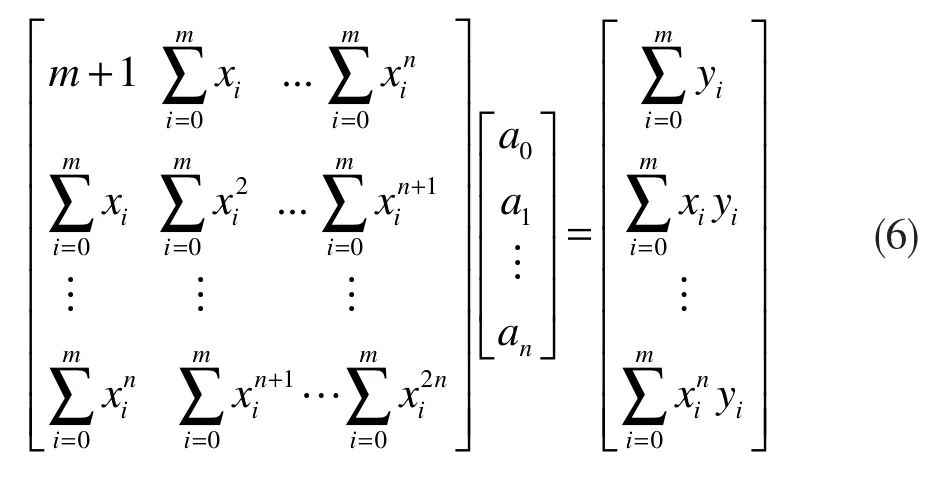
因此，只要給出坐標點(xi,yi)及其個數，再給出所要擬合的參數n，則可求出未知數矩陣[a0,a1,a2,...,an]。

3 地質測量實施應用

3.1 地質測量設計思路

地質測量的整體實施步驟及部分環節的設計理念如圖1 所示。根據地表形狀測繪出圖形，對圖形求解面積。由于平面面積的不規則性，按積分求解平面面積。為提高精確性，選取固定深度求解體積，統計礦產開采量，利用所記錄體積內的開采量，運用二乘法對數據建模，運用MATLAB 軟件編程，擬合成具體的函數曲線。

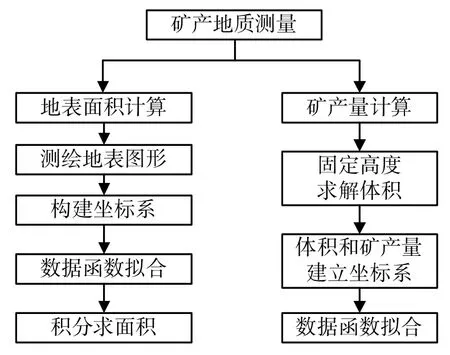
圖1 地質測量流程圖

3.2 平面面積計算理論

通過地表平面形狀，按比例縮小，測繪出具體的平面圖紙。利用平面直角坐標系計算圖紙面積，按比例放大，計算地表平面實際面積。平面面積計算可采取過蒙特卡洛方法，然而由于地表平面的不規則形狀，類似幾何概型面積比值求解的思路不適用于地質礦產精準的測量。在此種情況下，對平面面積的求解采用以X 軸為寬，Y 軸為長建立平面直角坐標系，為減小誤差寬度改變、遵循等差數列及公差較小的增長方式，以平面圖形長度的邊緣建立平面直角坐標系（x,y）。利用MATLAB 軟件對數據建模處理，擬合成y 與x（即平面長度與寬度）的具體函數表達式，利用積分思想求解面積。

不規則形狀的平面圖形積分法如圖2 所示。在區間[a,b]內分割成 n 份（n →∞），每份矩形面積的加和為最后整個區間的面積，即：

由于f(x)數據建模是根據冪指數擬合具體的函數圖像，所以f(x)在區間內是可積分的。把該積分的極限值定為該區間的定積分，即：

以此求出測繪圖形的具體面積，根據縮放比例求出地表平面的實際面積。

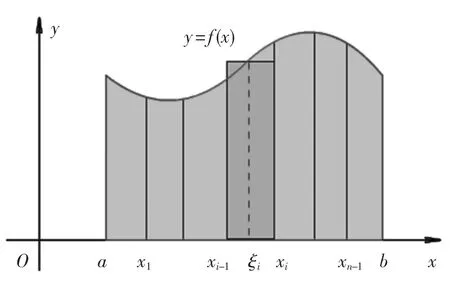
圖2 不規則形狀的平面圖形積分法

3.3 模擬面積仿真實驗

對數據的面積求解，模擬出擬合函數曲線。遵循上述平面面積求解理論，根據長度和寬度確定7組（x,y）坐標，具體為：（x1,y1）＝（-3,4）；（x2,y2）＝（-2,6）；（x3,y3）＝（-1,7）；（x4,y4）＝（0,9）；（x5,y5）＝（1,12）；（x6,y6）＝（2,34）；（x7,y7）＝（3,31）。運用數據建模的思想，結合MATLAB 軟件進行編程設計，對數據做多項式最小二乘擬合。利用已知的坐標呈現散點圖的形式，確定模擬參數的冪指數，根據數據確定矩陣，研究冪、行、列之間的關系式。根據方程確定系數，制作出具體的擬合函數曲線。實驗結果如圖3、圖4 所示，以多次擬合結果的兩種情況為例做出對比分析，圖3 是六次冪的擬合曲線，圖4 是五次冪的擬合曲線。基于最小二乘法圖像擬合原理，使散點圖中坐標點盡量多地落在回歸方程上，可果斷舍去五次冪的擬合圖像，選取六次冪擬合圖像。

圖3 六次冪擬合曲線

圖4 五次冪擬合曲線

用MATLAB 求出具體的系數 a(1), a(2)，...，a(7)數值，具體計算語句為：f(x)=(9.0000)+(-2.2737e-013)*x+(-0.8056)*x.^2+(-2.7500)*x.^3+(1.4444)*x.^4+(0.2500)*x.^5+(0.1389 )*x.^6。根據函數解析式，利用積分求解平面面積。以下代碼為MATLAB 軟件編寫圖像擬合過程的程序設計代碼：

4 礦產開采量測量

求得地表平面的面積，以深度的增長遵循等差數列公差（d＜1m）進行增長，通過 V=S·h 求得體積，并在開采過的礦產中統計該體積中的礦產量F，以體積作為X 坐標，實際的礦產量做為縱坐標建立多組數據（V,F）。運用最小二乘法算法，同上述地表面積求解過程的數據擬合方法類似，進行數據建模。采用冪指數形式擬合成具體曲線函數。根據不同冪指數的形式做多次擬合，選取散點圖盡量多的在曲線上選擇最高冪指數的擬合曲線。也可在MATLAB中進行編程設置，輸入數據后一次輸出多個最高冪指數擬合圖像。觀察坐標點在擬合曲線的多少，選擇擬合曲線函數，具體求解擬合參數的系數。為提高精確度、減小誤差，可在Excel 文件中建立多組數據，在MATLAB 中通過讀入的方式錄入數據。確定擬合曲線后，可根據曲線函數計算固定深度、固定面積礦產開采量、開采率、固定深度總開采量等數據。

經以上步驟，在大數據的支持下，可對不同地理位置和環境下的礦產數據進行數據建模，擬合成不同的曲線函數。相同條件下，遇到未開采的礦區時，可以從已建成的擬合曲線函數數據庫中，匹配函數曲線與解析式，通過深度和地形面積數據預測未開采礦區的開采量及固定體積下的開采數據等。

開采過程中，通過匹配擬合函數，可對某一體積下的開采率進行比對，研究開采狀態和未知狀況，為合理、科學開采提供參考及技術支持。

5 結束語

最小二乘法作為匹配數據的最優算法之一，廣泛的應用到各個領域，本研究將其應用到地質測量中。在大數據下，為減小誤差、遵循實用性的準則，針對開采過的礦區，運用最小二乘法法，以MATLAB軟件編程，對地表平面的面積、開采量等數據建模處理，以冪指數擬合方式確定具體擬合圖像，構造具體曲線函數解析式，建立多種地理環境下擬合函數數據庫。地表面積求解中擬合函數圖像與實際圖形結合，運用積分巧妙解決了不規則圖形面積求解問題。數據建模擬合的具體函數對今后新礦區的開采提供有利的、精確的數據支撐。數據模擬實驗對數據的建模處理提供了思路和方法，對理論數據和實際數據逼近提供了有利的保證，同時也驗證此算法在地址礦產測量中的實用性和可行性。