基于分數階微積分理論的最優導引律設計

顧 凱，金 岳，劉新宇

（北京航天微系統研究所，北京100094）

0 引言

研究與實踐表明，比例導引法形式簡單，調整方便，技術上易于實現，是目前應用最為廣泛的導引技術[1]。但是在打擊動目標時，由于缺乏目標的機動信息，在攔截末端視線角速率快速旋轉，從而易導致末端過載突變的情況[2]。為了解決這一問題，眾多學者進行了深入研究。文獻[3]提出了一種基于目標機動補償的增強型比例導引方法，該方法在比例導引法的基礎上增加了目標加速度補償項，從而降低了彈道末段的需用過載，但該方法需要高質量的目標加速，當目標加速度估計誤差較大時，制導性能便急劇下降。文獻[4]提出了一種滑模變結構制導律，該制導律對參數攝動和外界干擾不敏感，目標機動對其影響不大，但其存在抖振的問題，影響制導性能。文獻[5]提出了一種H∞制導律，該制導律無需目標加速度信息，但Hamilton-Jacobi微分不等式的求解比較困難，工程應用尚難實現。

分數微積分把微積分的階次推廣到了分數領域，其反映的不再是點或局部的性質，而是綜合考慮了歷史和全局分布式的信息，即分數階微積分具有記憶性。本文利用這一特點，同時結合最優控制理論，設計了一種分數階最優導引律。該導引律繼承了比例導引法良好的跟蹤性能，且能夠抑制視線角速率的快速旋轉，從而能夠解決比例導引法末端過載突變的問題。

1 分數階微積分的定義

一般分數階微積分的表達式為[6]

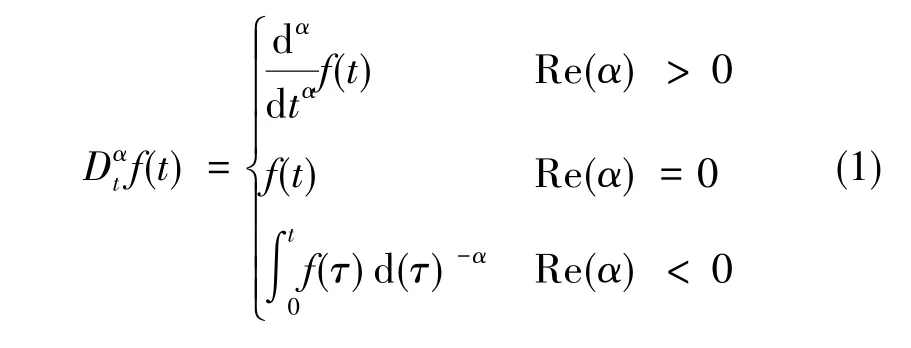
式（1）中，為微分或積分操作算子；α為微積分的階次，可以是實數或復數；Re（α）為α的實部。

不同數學家給出的分數階微積分定義形式有所不同，應用較多的三種微積分定義分別為Grünwald-Letnikov定義、 Riemann-Liouville定義和Caputo定義。

1.1 Grünwald-Letnikov（GL）定義

1.2 Riemann-Liouville（RL）定義

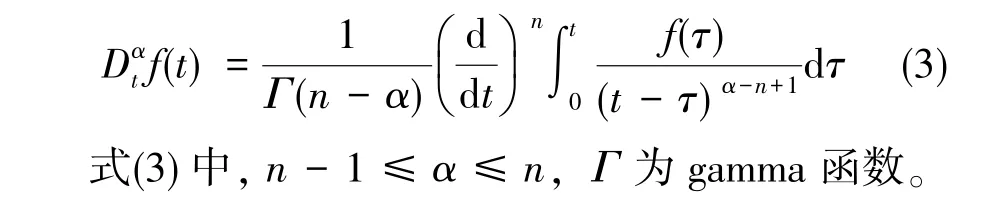
1.3 Caputo定義

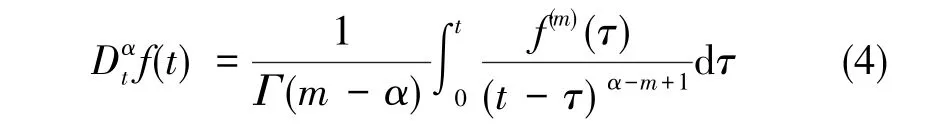
式（4）中，m－1≤α≤m，Γ為gamma函數。當t＞0時，若f（t）具有m+1階導數，則GL定義和RL定義是完全相等的。GL定義采用極限求和的方式定義分數階微積分，更適用于分數階微積分的數值求解。Caputo定義采用求導和積分運算，更適用于理論分析。

1.4 分數階微積分的性質

根據分數階微積分的定義，可以得到分數階微積分具有如下性質[7]:

1）分數階微積分具有記憶性質。由分數階微積分的定義式，函數f（t）在某一點上的分數階微分與整數階微分是不同的。分數階微分并不是在這一點處求極限，而是與初始時刻到該點以前所有時刻的函數值有關，故分數階微積分具有記憶性。

2）分數階微積分具有線性性質，即

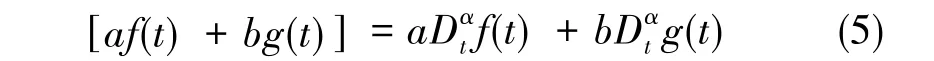
3）分數階微積分具有疊加性質，即

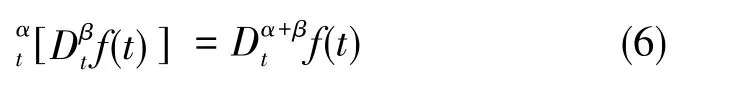
4）解析函數的分數階導數對t和α都是解析的。

5）當α＝n、n為整數時，分數階微分與整數階n階微分結果是一樣的。

6）當α＝0時，

2 分數階微積分算子的數字實現

分數階系統通常無法用確定的解析表達式表達，因此在仿真分析或工程實際應用中，需要采用數值求解的方法。目前，常用的數字實現算法包括:基于GL定義的短記憶法，基于Euler算子的PSE展開法，基于Tustin算子、Simpson算子和Al-Alaoui算子的 CFE展開法，以及遞歸式展開法。這些算法雖然在幅頻特性上獲得了較好的近似，但在相頻特性上的近似精度不高。Oustaloup濾波器在頻率響應中的幅頻特性及相頻特性均具有很好的近似，但在頻率段端點附近的擬合效果并不理想。有學者研究了一種改進算法，提高了分數階模型的擬合精度。本文采用改進的Oustaloup數字算法來實現分數階微積分算子s±α的數值計算。

將該濾波器在Matlab上進行模塊封裝，如圖1所示。

圖1 分數階微積分算子Fig.1 Diagram of fractional calculus operator

3 彈目相對運動模型

導彈的三維制導模型可以通過忽略耦合并將其分解到兩個相互垂直的平面進行解決，本文以縱向平面為例建立了彈目相對運動模型，如圖2所示，并做如下假設:

圖2 彈目相對運動關系Fig.2 Diagram of relative motion relationship between missile and target

1）將導彈和目標均視為質點；

2）導彈的速度和目標的速度大小保持不變。

根據圖2的幾何關系，可以推導出導彈和目標的相對運動方程

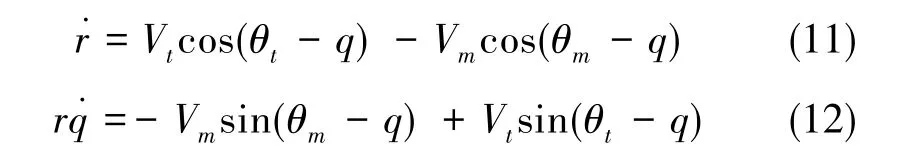
對式（12）求導并將式（11）代入， 可得

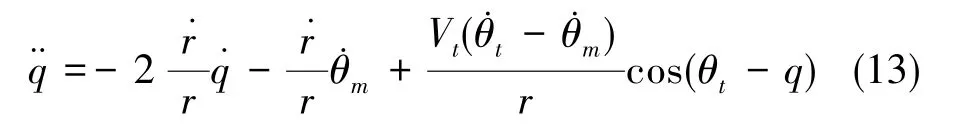
式（13）中，Vm和Vt分別為導彈和目標的速度，q和˙q分別為彈目視線角和彈目視線角速率，θm和θt分別為導彈和目標的速度方向角。

在導引律的設計過程中，可將˙θm視為控制系統的輸入，將含有目標未知信息的耦合量視為外部的擾動。因目標的運動信息難以獲取，在導引律的設計過程中無法完成對擾動的補償，從而導致傳統的比例導引法在打擊機動目標時會出現由于在彈道末端彈目視線角速率迅速增加而使所需過載過大的問題。為了解決這一問題，根據1.4節中分數階微積分的記憶性和疊加性，設計了基于分數階微積分的最優控制導引律。該方法以最小過載為性能指標，能夠抑制彈道末端視線角速率的迅速增加，解決了末端過載過大的問題。

4 制導律的設計

將含有目標的未知信息當作外界擾動，則制導模型如下[9]

相比傳統比例導引法，本文所設計的導引律含有視線角速率的分數階微分項。由分數階微積分記憶性可知，視線角速率的分數階微分不只是某一點的微分項，而是包含了視線角速率從初始時刻到現在的所有歷史信息[10]，從而能夠抑制視線角速率的突變，解決了比例導引法在打擊機動目標時末端過載迅速增加的問題。

5 仿真驗證

為了驗證所設計的分數階微積分最優導引律的正確性和有效性，本文在Matlab環境下進行了仿真驗證，并與傳統比例導引法進行了比較，導引律中的分數階微分項通過上述封裝的Oustaloup濾波器來近似實現。

仿真條件如表1所示。

表1 仿真條件Table 1 Simulation conditions

比例導引系數K的取值范圍為（2，6）[11]，分數階微分的階次μ在（0，1）內取值。由分數階微積分的性質可知，當微分階次取整數時，分數階微分與整數階微分的結果是一樣的。參數選取設為k1＝K、k2＝1－μ，即分數階最優導引律的邊界情況可以歸結為比例系數K和K+1的情況，以此與傳統比例導引法進行對比。根據文獻[12]，將本次仿真中的K設為3，采用遍歷尋優法，μ的取值為0.8。

進行仿真驗證，結果如圖3、圖4所示。

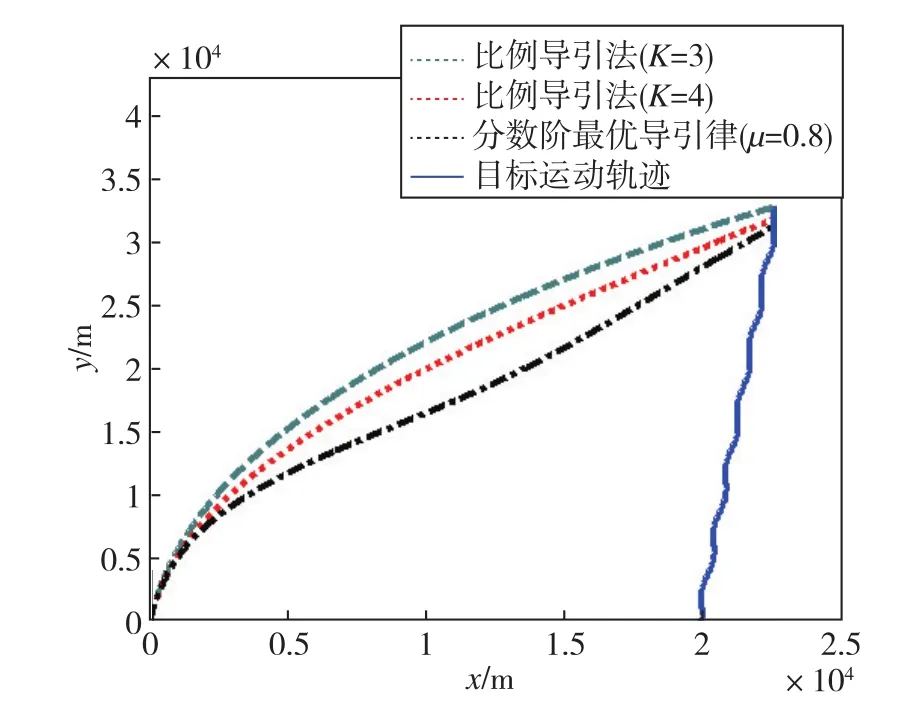
圖3 攔截曲線Fig.3 Diagram of interception curves

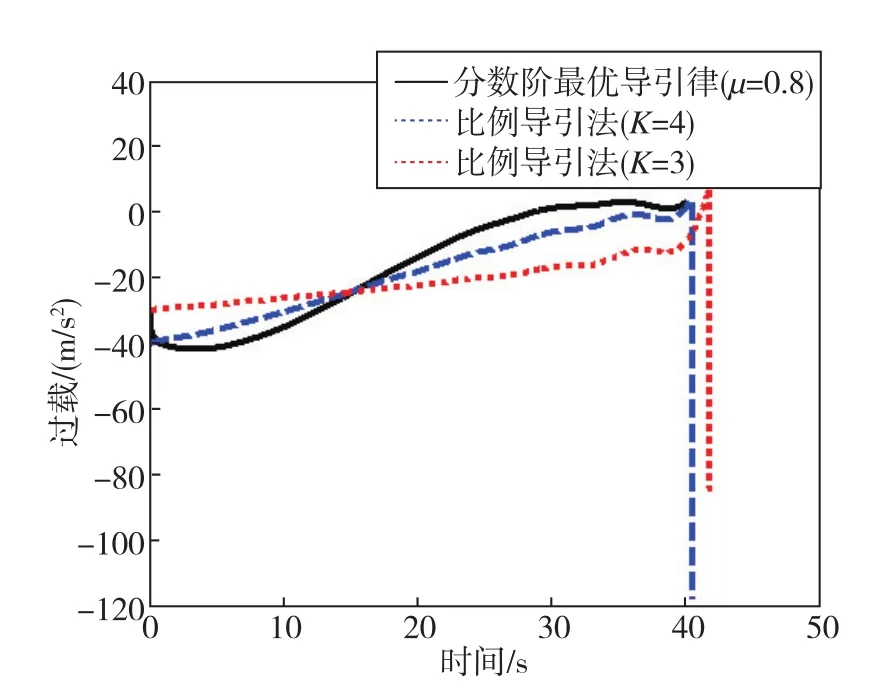
圖4 彈的過載曲線Fig.4 Diagram of missile overload curves

由圖3可以看出，分數階最優導引律能夠保持傳統比例導引法良好的跟蹤性能，能夠準確地命中目標。

由圖4可以看出，在15s之前，分數階最優導引律下的過載大于比例導引法；在15s之后，分數階最優導引律下的過載明顯小于比例導引法下的過載。由此可見，分數階最優導引律的過載分布更為合理。在導彈命中末端，比例導引法過載值會突然增大，這在實際情況下往往無法達到，從而會導致脫靶。而分數階最優導引律能夠很好地解決這一缺陷，彈的過載在飛行的后半段幾乎趨近于0，且在末端沒有突變。分數階最優導引律的命中時間為40s，K＝3時的比例導引法的命中時間為42s，K＝4時的比例導引法的命中時間為40.9s。由此可知，分數階最優導引律能夠更快地命中目標。

6 結論

本文將分數階微積分理論與最優控制理論相結合，設計出了一種新的分數階最優導引律。該導引律繼承了比例導引法良好的跟蹤性能，同時解決了比例導引法在打擊動目標時末端過載突然增大的問題。仿真結果表明，相比比例導引法，分數階最優導引律命中時間短，過載分布更為合理，且末端過載無突變，趨近于0。