多路分流齒輪傳動系統的非線性振動特性研究

□ 戴日輝1 □ 王三民 □ 蘇 欣3 □ 周啟航

1.海軍駐哈爾濱地區第三軍事代表室 哈爾濱 150078 2.西北工業大學 機電學院 西安 710072 3.中國船舶重工集團公司 第703研究所 哈爾濱 150078

1 研究背景

在艦船、直升機、盾構機等裝備的動力傳動領域中,越來越廣泛地采用多路分流齒輪傳動系統,其中功率二分支齒輪傳動系統是最典型的一種多路分流齒輪傳動系統。在功率二分支齒輪傳動系統中,第一級主動齒輪同時與兩個從動齒輪嚙合,實現功率的分路傳遞。第一級的兩個從動齒輪與第二級的兩個主動齒輪分別通過花鍵連接,第二級的兩個主動齒輪同時與并車齒輪嚙合,實現功率的匯流輸出。由于這種傳動系統全部采用定軸輪系,因此克服了行星齒輪傳動系統行星輪離心力大的缺陷[1]。

雖然有關行星齒輪傳動系統的動力學特性和均載特性的研究論文較多[2-7],但目前針對多路分流齒輪傳動系統的動力學研究成果相對較少。1996年,Krantz等[8-9]開展了功率二分支齒輪傳動系統最優均載設計的理論和試驗研究。2003年,Kartik等[10]建立了功率二分支齒輪傳動系統的動態傳動誤差分析模型,并研究了齒輪幾何參數對傳動系統動態傳動誤差的影響規律,揭示了功率分支傳動系統中齒輪副的相差現象。2004年,Fussner等[11]研究了功率分支齒輪傳動系統中齒輪參數和軸的偏斜運動對嚙合效率的影響規律,建立了高效率功率分支齒輪傳動的優化設計方法。2005年,歐衛林等[12]提出了進行復雜齒輪系統動力學分析的軸單元法,并將其應用于功率分支系統的線性振動分析。最近幾年,西北工業大學多名教授及研究人員分別對功率分支齒輪系統的動態特性進行了研究,為減振降噪設計奠定了基礎[13-16]。

針對功率分支齒輪傳動系統已開展的振動特性研究大都采用的是線性模型,不考慮齒輪嚙合側隙和時變嚙合剛度等非線性因素的影響,因此無法解釋這種傳動系統在實際工作過程中出現的次諧、超諧等振動特性。筆者針對功率二分支齒輪傳動系統建立了傳動系統的扭轉振動動力學模型,引入齒側間隙函數來描述齒輪側隙,采用傅里葉級數來描述齒輪副嚙合剛度,形成齒輪傳動系統的非線性振動方程,采用數值方法求解系統的非線性響應,分析了工況參數對振動特性的影響規律。

2 非線性振動模型與方程

圖1所示為船用功率二分支齒輪傳動系統。

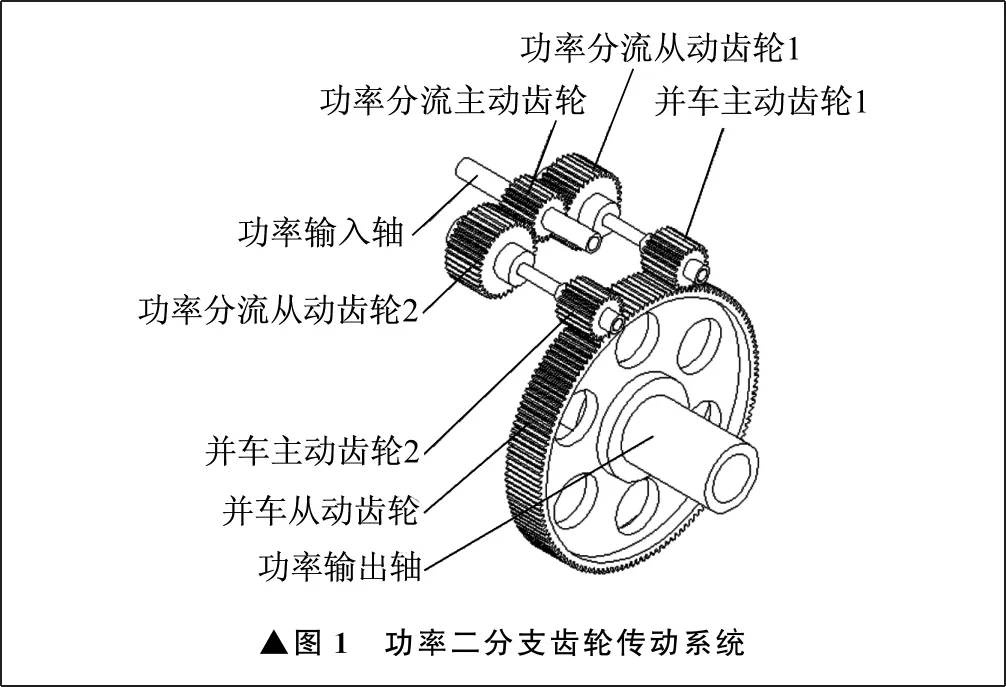
▲圖1 功率二分支齒輪傳動系統

圖2所示為功率二分支齒輪傳動系統振動動力學模型。圖2中共有八個集中質量,包括六個齒輪和原動機、螺旋槳。僅考慮每個集中質量的扭轉振動,因此共有八個振動自由度。這一動力學模型綜合考慮了齒輪副的時變嚙合剛度、每對齒輪副的齒側間隙,以及齒輪副綜合傳動誤差和原動機的輸入轉矩波動等因素。設原動機、六個齒輪、螺旋槳的扭轉振動位移為φh,h=1，2，…，8,由牛頓定理可推導出系統的非線性振動微分方程為：

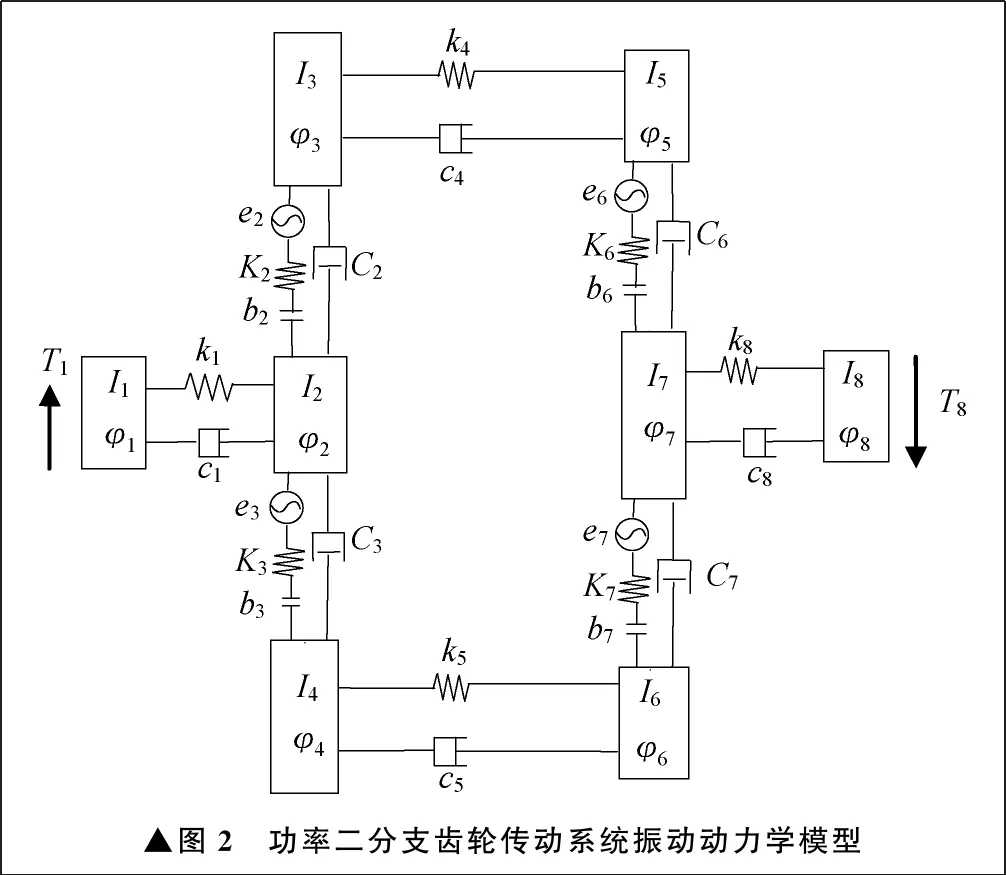
▲圖2 功率二分支齒輪傳動系統振動動力學模型

(1)

-e3,b3)=0

(2)

(3)

(4)

=0

(5)

=0

(6)

=0

(7)

(8)

f(rb2φ2-rb3φ3-e2,b2)、f(rb2φ2-rb4φ4-e3,b3)、f(rb5φ5-rb7φ7-e6,b6)和f(rb6φ6-rb7φ7-e7,b7)為齒側間隙非線性函數,將其統一表達為f(x,b),則定義為:

(9)

(10)

3 振動方程處理

為消除系統轉動的剛體位移,采用相對位移xh作為廣義坐標。

x1=rs1(φ1-φ2)

(11)

x2=rb2φ2-rb3φ3-e2

(12)

x3=rs4(φ3-φ4)-e3

(13)

x4=rb4φ4-rb7φ7

(14)

x5=rb2φ2-rb5φ5

(15)

x6=rs5(φ5-φ6)-e6

(16)

x7=rb6φ6-rb7φ7-e7

(17)

x8=rs8(φ7-φ8)

(18)

式中：rsj為各傳動軸的半徑。

另外,振動微分方程式(1)～式(8)中各物理量的數值差別較大,這樣會給求解計算帶來較大誤差,因此在求解計算之前應對系統振動微分方程進行無量綱化處理。

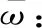
τ=tωp

(19)

(20)

式中：ωp為傳動系統的一階扭轉振動固有頻率。

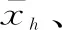
(21)

(22)

(23)

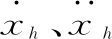
將式(11)～式(23)代入式(1)～式(8),并經過整理，可得到系統無量綱化的非線性振動微分方程：

(24)

(25)

(26)

(27)

(28)

=0

(29)

=F8

(30)

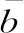
4 振動方程數值求解

對于非線性振動微分方程式(24)～式(30)，采用四階變步長龍格-庫塔數值法求解。首先將該二階非線性微分方程轉化為一階狀態微分方程的初值問題。

(31)

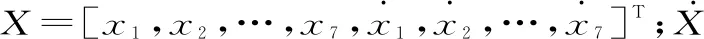
數值方法求解式(31)的基本思路是:對于給定的初始時間t0和終止時間td,取足夠大的正整數N,將時間段[t0,td]離散為N段:

tk=t0+kΔt

(32)

Δt=(td-t0)/Nk=0,1,…,N

(33)

式中：tk為第k個時間點;Δt為時間步長。

在時間間隔[tk,tk+1]內對式(31)進行積分,根據積分中值定理,存在sk∈[tk,tk+1]，使：

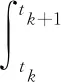
=X(tk)+f[X(sk),sk]Δt

(34)

式中：tk+1為第k+1個時間點；sk為tk至tk+1時間段中的時間點；s為tk至tk+1時間段中的時間。

若能通過某種計算方法得到sk的近似值,則可獲得X(t)在[t0,td]上的離散近似值Xk。

5 系統非線性動力學特性

功率二分支齒輪傳動系統的參數見表1。

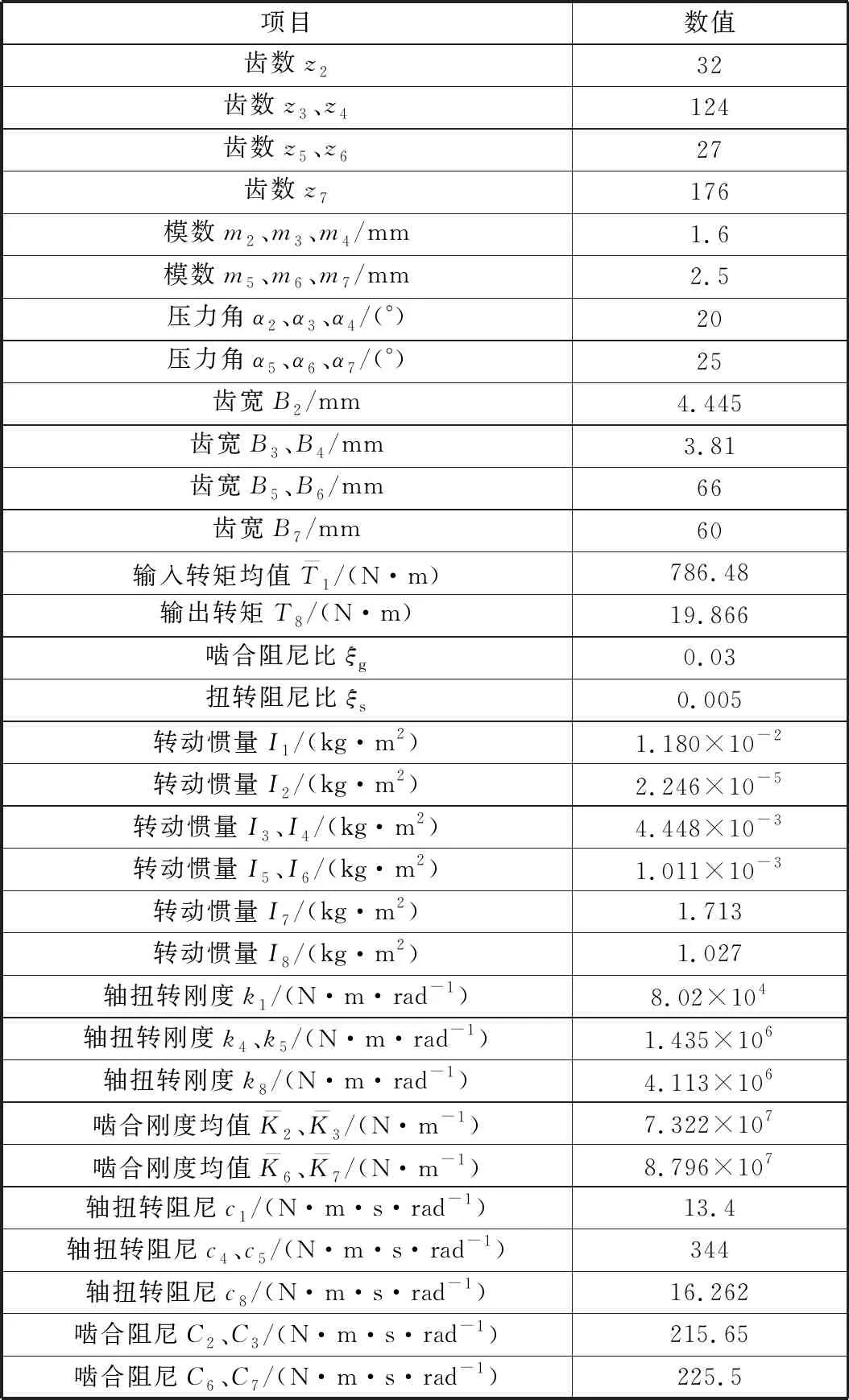
表1 功率二分支齒輪傳動系統參數

取各齒輪副的齒側間隙bl為100 μm,各齒輪副的綜合傳動誤差elm為10 μm，時變嚙合剛度表示為均值和一階諧波分量之和的形式,即:

(35)

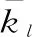
齒輪副的綜合傳動誤差可表示為:

(36)

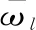
▲圖3 ω—為0.75時一周期響應

由圖3～圖6可以看出,隨著系統無量綱角頻率的變化,與線性振動系統不同的是,非線性系統的振動形態會發生本質變化,即除了與無量綱角頻率相同的簡諧響應之外,系統還會出現超諧波、擬周期，以及混沌響應。

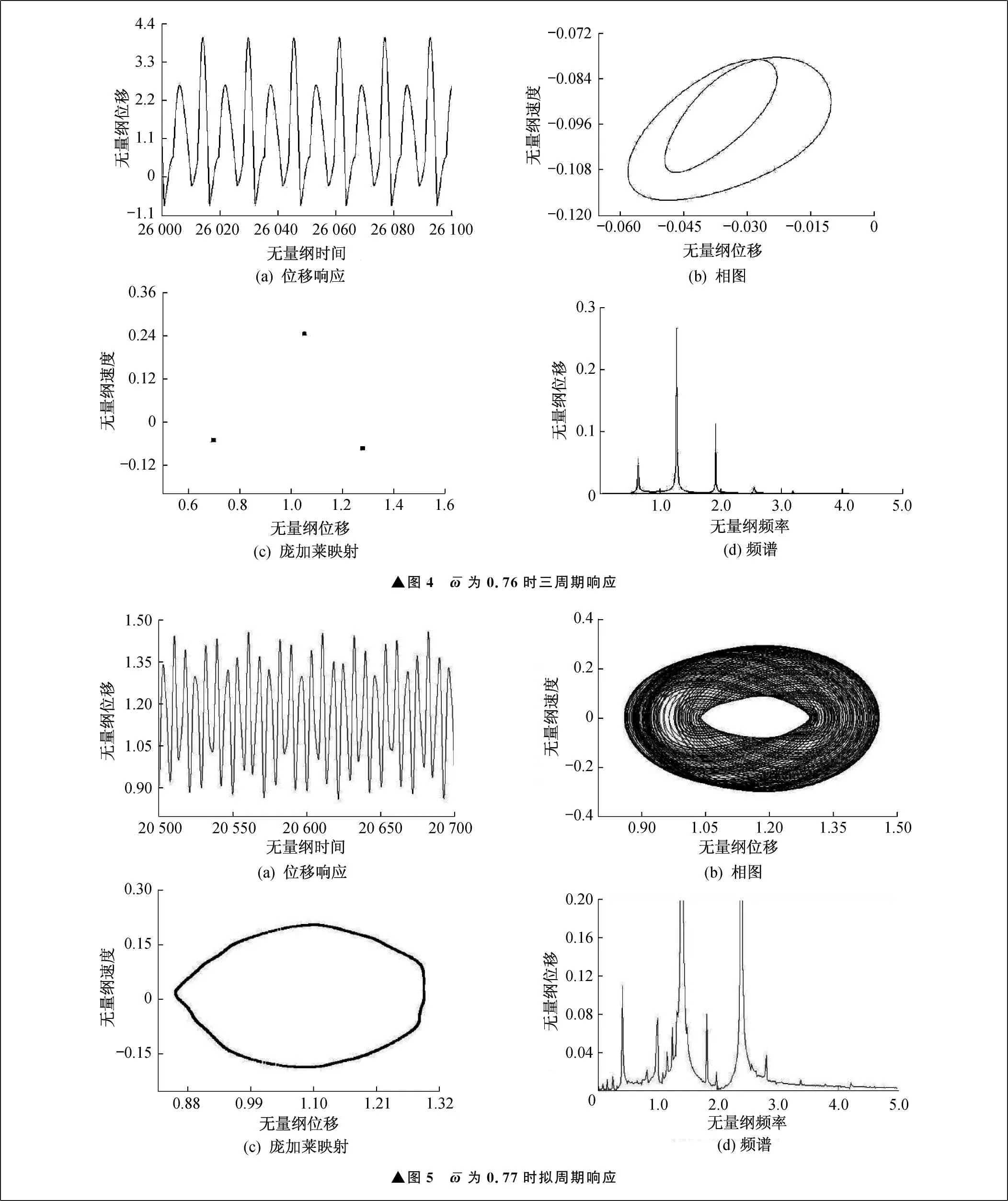
▲圖4 ω—為0.76時三周期響應▲圖5 ω—為0.77時擬周期響應

▲圖6 ω—為0.80時混沌響應

6 結束語

將功率二分支齒輪傳動系統簡化為八個集中質量和八個自由度的扭轉振動模型,采用間隙函數描述齒側間隙,采用傅里葉級數描述齒輪時變嚙合剛度,形成非線性振動微分方程。

由于齒側間隙和時變嚙合剛度的存在,功率二分支齒輪傳動系統的振動響應表現出較強的非線性振動特點,即不僅存在簡諧響應,而且還存在超諧響應和混沌響應。