仿生正弦前緣對翼面動態失速的影響
侯宇飛,李志平
1. 北京航空航天大學 能源與動力工程學院,北京 100083 2. 北京航空航天大學 航空發動機氣動熱力國家重點實驗室,北京 100083 3. 北航(四川)西部國際創新港科技有限公司,成都 610200
直升機在前飛狀態下為了平衡槳盤升力,需增大后行槳葉迎角。在高速前飛、重載飛行等典型工況下, 劇烈變化的迎角將造成槳葉動態失速。失速槳葉最大升力系數顯著提高,但強烈的非定常分離和氣動載荷變化是振動的來源,不僅嚴重限制直升機飛行包線還降低了結構壽命,還可能引發附加的氣動阻尼[1]。因此,有效控制動態失速是改善旋翼流動特性和提升直升機飛行性能的關鍵。
翼型氣動載荷的劇烈變化與前緣分離渦的產生、發展和脫落關系密切。當翼型上仰超過靜態失速迎角后,分離渦在前緣上表面形成并快速向下游移動,旋渦的低壓效應使升力增加,隨后作用于尾緣造成低頭力矩激增,當旋渦脫離翼型表面,升力驟降。針對這種前緣分離渦目前已經發展出一系列控制方法,主動控制有下垂前緣[2]、固定前緣條[3-4]、前緣噴氣[5]、后緣小翼[6]。盡管它們在抑制分離渦方面取得了不錯效果,但動態控制裝置勢必造成結構復雜,重量增加,生產和維修成本上升[7],相比而言被動控制實施難度更小。
近年來,座頭鯨胸鰭前緣的凸起引起學者們極大興趣。作為一種被動控制,突起前緣顯著增強了座頭鯨的機動性,使其形成獨特的180°U型回轉捕食方式[8]。大量靜態研究表明,前緣突起能夠在高迎角下提高升力,推遲失速。Watts和Fish[9]應用小板理論對翼面進行數值模擬,表明凹凸前緣在10°迎角下升力增加4.8%,阻力減小10.9%。Miklosovic等[10]通過風洞試驗發現凹凸前緣翼面在雷諾數Re=5×105下失速迎角增大40%,最大升力提高6%。關于流動機理,學者普遍認為前緣凸起類似于渦流發生器[11-13],其產生的高強度流向渦增強了邊界層與主流區域的動量交換,是增加升力和推遲失速的關鍵,Stanway[14]運用粒子圖像測速(PIV)法技術證實了這一點,發現在大迎角下前緣波峰間形成了沿流向的反向渦對。同時流向渦產生的下洗流動[15-16]促使流動貼附在翼型上表面,因而推遲失速。此外,文獻[8,11]還提出這種凸起結構相當于翼刀,抑制了分離區沿展向傳播。目前關于將仿生凹凸前緣運用到動態失速控制的研究較少,Borg[17]通過試驗研究了雷諾數為1.3×105下不同凹凸前緣對NACA0012動態失速特性的影響,發現減小凸起間距和凸起幅度能夠增大升力峰值,減小遲滯效應。在雷諾數為1×106下[18],波狀凸起前緣同樣提升了NACA0012動態失速平均升力。文獻[17]只研究了仿生凹凸前緣對氣動載荷的影響,沒有進行流動機理分析。文獻[18]旨在提高動態失速下機翼的升力,未考慮凹凸前緣對阻力和俯仰力矩的影響,并且未討論凹凸幾何參數對流場的作用。
鑒于凹凸前緣在直升機旋翼動態失速控制方面的潛力,為了將其應用在工程實踐中,有必要深入理解凹凸前緣流動控制機理。本文基于試驗驗證的數值模擬方法,研究了仿生前緣對翼面動態失速的抑制作用,重點關注對分離渦的影響機理,對比了不同前緣幾何的氣動特性。同時為了探究仿生前緣的作用范圍,討論了平均迎角、迎角振幅、折算頻率以及來流馬赫數對其動態失速控制效果的影響。
1 幾何模型與數值方法
1.1 仿生凹凸前緣造型
選取SC1095旋翼翼型為研究對象,它被應用于美國黑鷹直升機主槳,分布在0.85R(R為槳盤半徑)以外展向位置,是動態失速經常發生的區域。原型翼由SC1095翼型沿槳葉展向無扭轉拉伸而成,展長為0.5倍翼型弦長。采用正弦函數模化仿生凹凸前緣,翼面弦長沿展向的分布為
C(z)=C+Acos(2πz/λ)
(1)
式中:z為展向坐標;C(z)為翼面展向各截面弦長;C為原型翼弦長;A為正弦前緣波峰;λ為正弦前緣波長。
參考座頭鯨胸鰭前緣外形[19],A分別取0.025C、0.050C和0.100C,λ分別取0.25C和0.50C,3種波峰和2種波長組合生成6種正弦前緣翼作為研究對象。圖1給出了原型翼和正弦前緣翼示意圖,經驗證[18]當兩側設為周期性邊界條件時,展向的正弦周期數目不影響計算結果,因此為減少計算量本文正弦前緣翼沿展向均取1個周期。為保證只有翼面前緣做正弦修型而不改變其他區域幾何,翼面尾緣沿展向對齊,只對前緣(最大厚度之前)進行縮放處理(見圖2),其表達式為
(2)
ynew=yoriginal
(3)
式中:x為橫坐標;y為縱坐標;“original”代表原型翼;“new”代表正弦前緣翼;“mt”代表原型翼最大厚度位置;坐標原點位于尾緣。

圖1 原型翼和正弦前緣翼俯視圖Fig.1 Top view of prototype wing and sinusoidal leading-edge wing

圖2 翼型前緣縮放示意圖Fig.2 Schematic diagram of scaling of airfoil leading-edge
1.2 網格生成與數值方法驗證
為確保計算結果不受邊界條件影響,計算域取100倍弦長(如圖3所示)。計算全部采用結構網格,同時在翼型周圍方形區Ⅰ及尾跡區Ⅱ進行網格加密處理, 通過拉伸生成展向網格。定義全部網格做整體剛性俯仰運動來模擬動態失速,不僅能夠保證網格質量不變,還避免了使用動靜交界面產生的數據傳遞誤差。所有外場邊界定義為同一個速度進口邊界,因而轉動到任一迎角時進口面積始終等于出口面積。在滿足總體質量連續的情況下,使用唯一速度同時定義進/出口是可行的[20]。翼型表面為無滑移條件,展向兩側為周期性邊界條件。如圖4所示,翼型附近采用O型網格,表面第1層網格高度使y+最大不超過2。
驗證案例取自文獻[21]的試驗結果,Re=3.92×106,馬赫數Ma=0.3,翼型以折算頻率k=0.1做正弦俯仰, 轉軸在距前緣25%弦長處。采用3種不同數目的網格來驗證網格無關性,分別為64萬、160萬和288萬。為及時捕捉失速渦的發展動態,將1個俯仰周期分為1 000個時間步。假設流動為完全發展的湍流,考慮到Spalart-Allmaras(S-A)模型和k-ωSST(Shear Stress Transport)模型在預測翼型動態失速方面都有廣泛應用,這里對二者計算結果進行了比較。采用壓力基求解器,搭配Coupled算法。相比于Simple和Piso算法,Coupled算法能更快達到收斂,尤其對長時間步具有較高魯棒性[22]。下文以CL表示升力系數,CD表示阻力系數,Cm表示俯仰力矩系數,α表示迎角。參考長度為弦長,參考面積為弦長×展長,俯仰力矩參考點為轉軸處。

圖3 計算域示意圖Fig.3 Schematic diagram of computational domain

圖4 翼型附近的O型網格Fig.4 O-block mesh around airfoil
圖5給出了驗證案例計算結果,通過對比試驗結果,看到在上行(迎角增大)過程中,兩種湍流模型均能準確地預測氣動載荷,包括失速迎角和升力系數峰值。但是在下行(迎角減小)過程中,計算結果與試驗值有一定偏差,這與分離后的湍流具有強非平衡性有關,而模型參數由簡單流動獲得。S-A模型在失速迎角附近預測的氣動性能出現大幅振蕩,且計算得到的抬頭力矩峰值和低頭力矩峰值較于k-ωSST偏差更大,因此采用k-ωSST模型。中等密度網格結果已不受網格數目增加的影響,在下文的計算中均采用中等數量網格。總體可見,本文采用的數值方法能夠模擬動態失速。
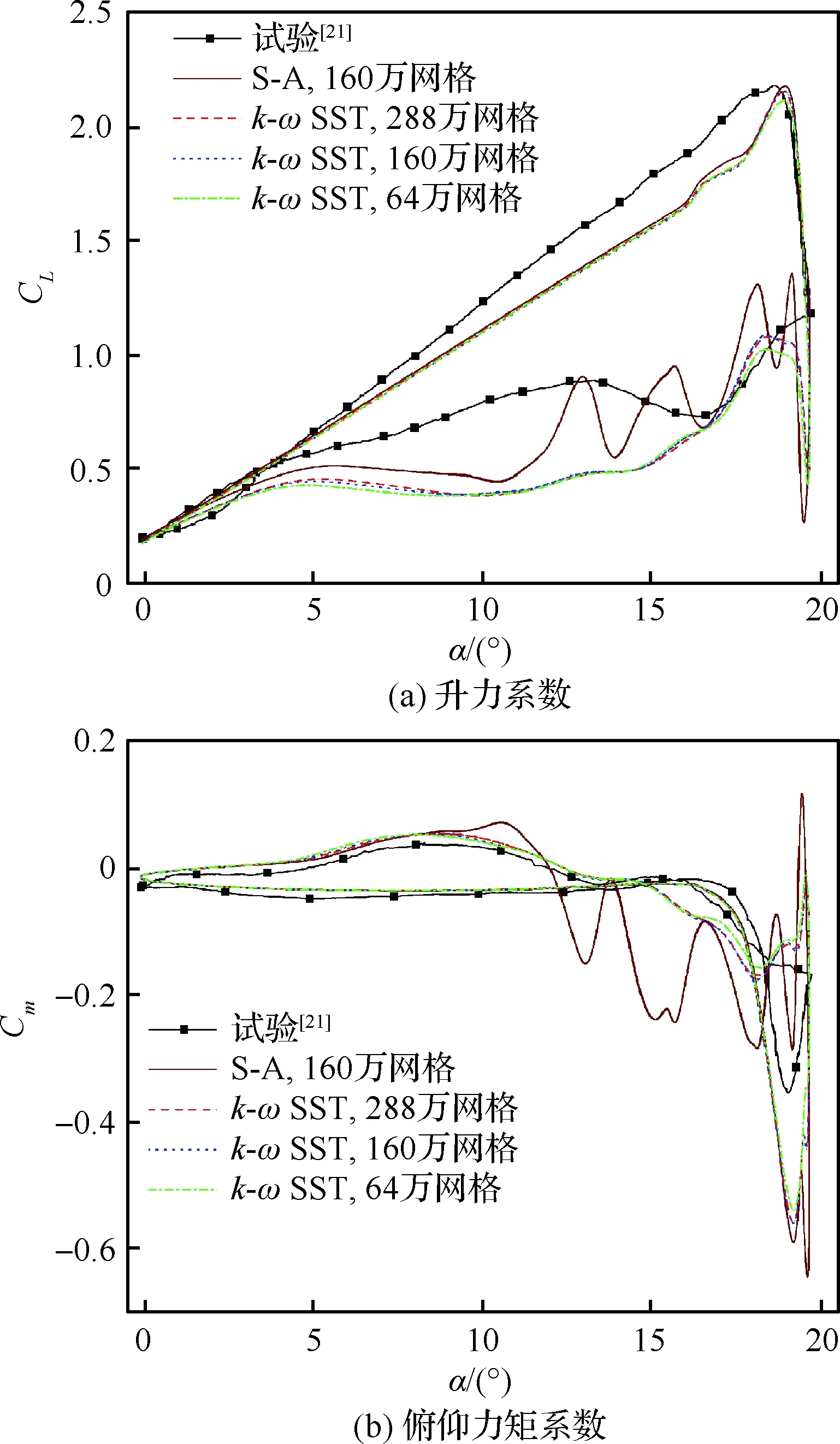
圖5 計算值與試驗值的對比Fig.5 Comparison between calculated and experimental values
2 仿生前緣動態失速控制機理分析
針對1.2節中案例,表1列出了6種仿生正弦前緣翼的幾何參數與計算結果,包括最大升力系數CLmax、最大阻力系數CDmax、最大俯仰力矩系數Cmmax相較于原型翼的變化量(ΔCLmax、ΔCDmax和ΔCmmax)。仿生前緣在減小載荷幅值方面展現出巨大潛力,6種造型均能顯著降低阻力峰值和低頭力矩峰值,這對降低振動載荷和增加槳葉壽命很有必要。盡管都伴有不同程度的升力損失,但急劇變化的俯仰力矩是動態失速中最嚴重的問題,是顫振邊界的成因,而一定的升力峰值減小可以接受,這是因為直升機在高前進比下升力主要由前后側槳盤60%~85%半徑區域產生,而動態失速通常發生在左側槳盤85%半徑以外區域[23]。可以看到隨著波峰的增加和波長的減小,阻力和力矩峰值減小量增加,但升力系數損失也有所增加。其中A025W5、A05W5和A025W25以較小的升力代價獲得了明顯的阻力特性和力矩特性的提升。

表1 正弦前緣翼案例及結果匯總
本節以A05W5為例,對比原型翼分析其動態失速控制機理。當迎角分別上行至8.49°、10.35°和11.89°時,CL均保持線性增長(如圖6(a)所示),流動附著于翼面。各截面壓力系數(Cp)對比由圖7給出,Original代表原型翼截面,Peak代表波峰截面,Trough代表波谷截面。隨著迎角增加,原型翼吸力峰值有所增加,而波谷截面吸力峰值顯著增加,在迎角為11.89°時Cp超過了-10,這是因為部分氣流從波峰向波谷匯聚,速度增加形成了高負壓區和強逆壓梯度。反過來,一部分將要抵達波峰的氣流被波谷前緣的負壓抽取過去,使得波峰前緣繞流加速效果減弱,因此波峰截面Cp峰值始終較小。
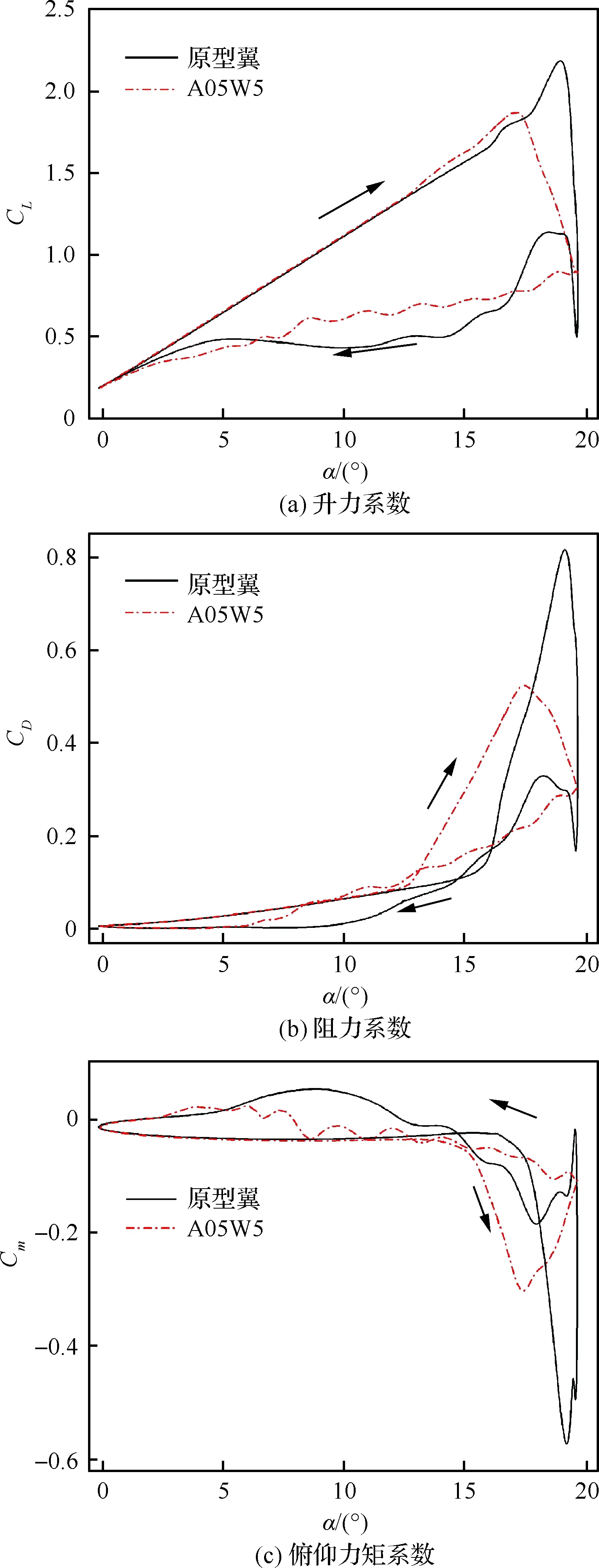
圖6 原型翼與仿生翼A05W5氣動系數對比Fig.6 Comparisons of aerodynamic coefficients between original wing and bionic wing A05W5
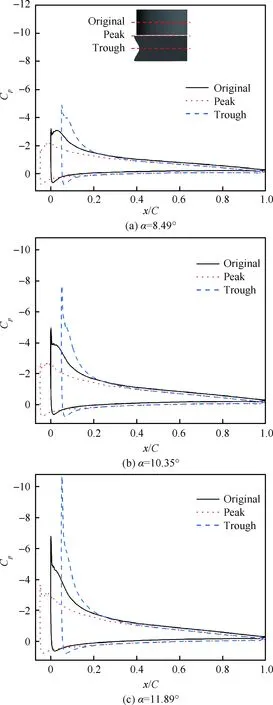
圖7 不同截面壓力系數對比Fig.7 Comparisons of pressure coefficients on different sections
圖8和圖9給出了迎角上行至12.8°時的各截面壓力系數分布和流場,此刻A05W5的CL增長率發生了變化,原型翼CL仍位于線性增長區。流經波谷的氣流在更短的行程內升壓至平均水平,產生的強逆壓梯度使波谷更易分離,提前出現了分離渦,其附帶的的低壓效應使得波谷截面Cp出現“小平臺”,進一步增加了波谷截面翼型的升力,從而改變CL斜率,這與Carr等[24]的結論一致。原型翼與波峰截面均保持附著流動。
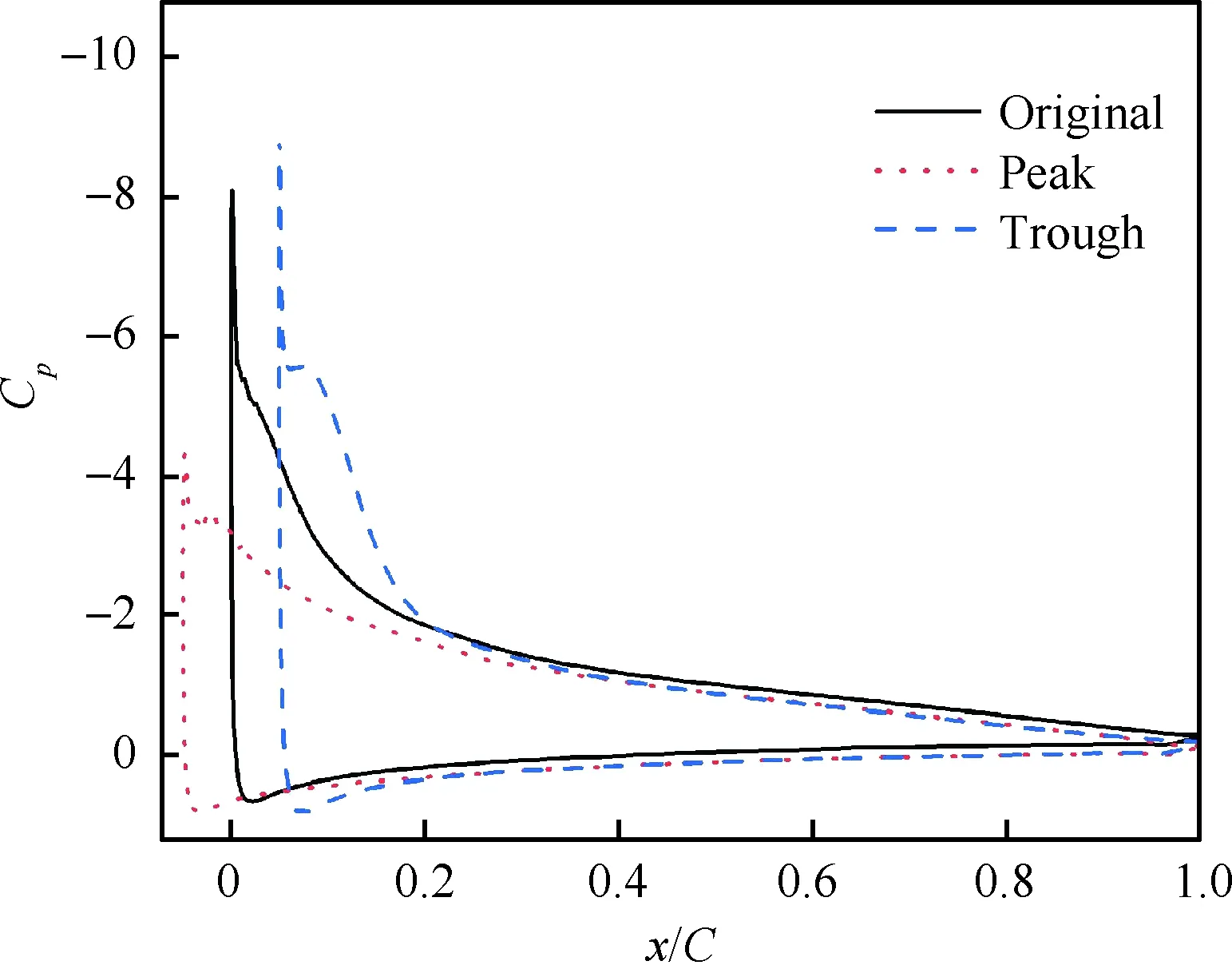
圖8 α=12.8°時不同截面的壓力系數Fig.8 Pressure coefficients on different sections at α=12.8°
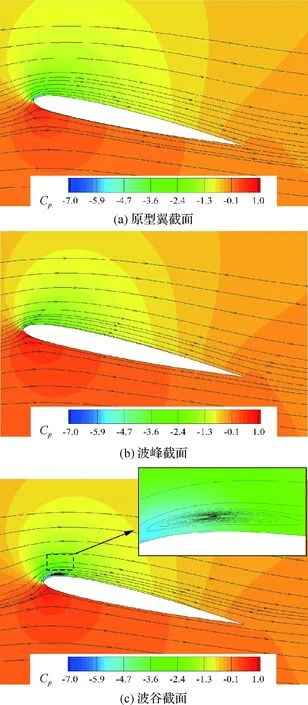
圖9 α=12.8°時不同截面的流場Fig.9 Flow fields on different sections at α=12.8°
圖10和圖11展示了迎角上行至16.05°時的各截面壓力分布與流場。原型翼CL增長率出現變化,較于A05W5推遲了約3.3°,同樣在脫離CL線性增長區時觀察到前緣分離渦。然而波谷在α=12.8°時產生的分離渦更早進入下游,覆蓋了約60%波谷截面上表面,從Cp曲線圖看出分離渦形成的低壓區向下游移動,升力繼續增加,壓差阻力和低頭力矩同時增大。波峰截面流動基本附著,但因為受到波谷分離渦牽動,波峰截面尾緣上游流線扭折,出現回流和展向流動,被牽動的氣流在一定程度上限制了分離渦的發展。
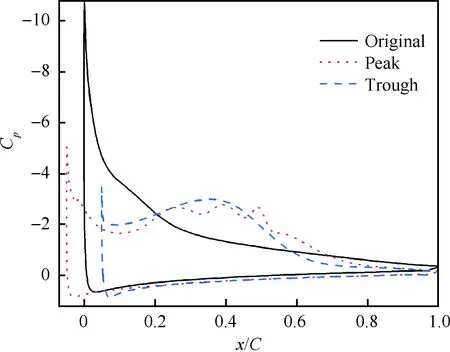
圖10 α=16.05°時不同截面的壓力系數Fig.10 Pressure coefficients on different sections atα=16.05°
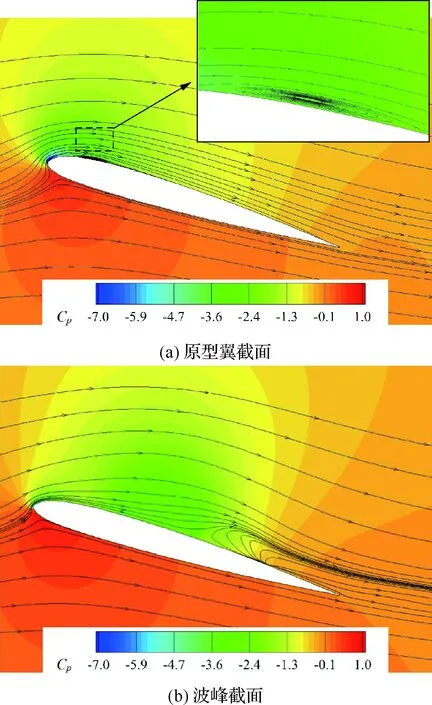
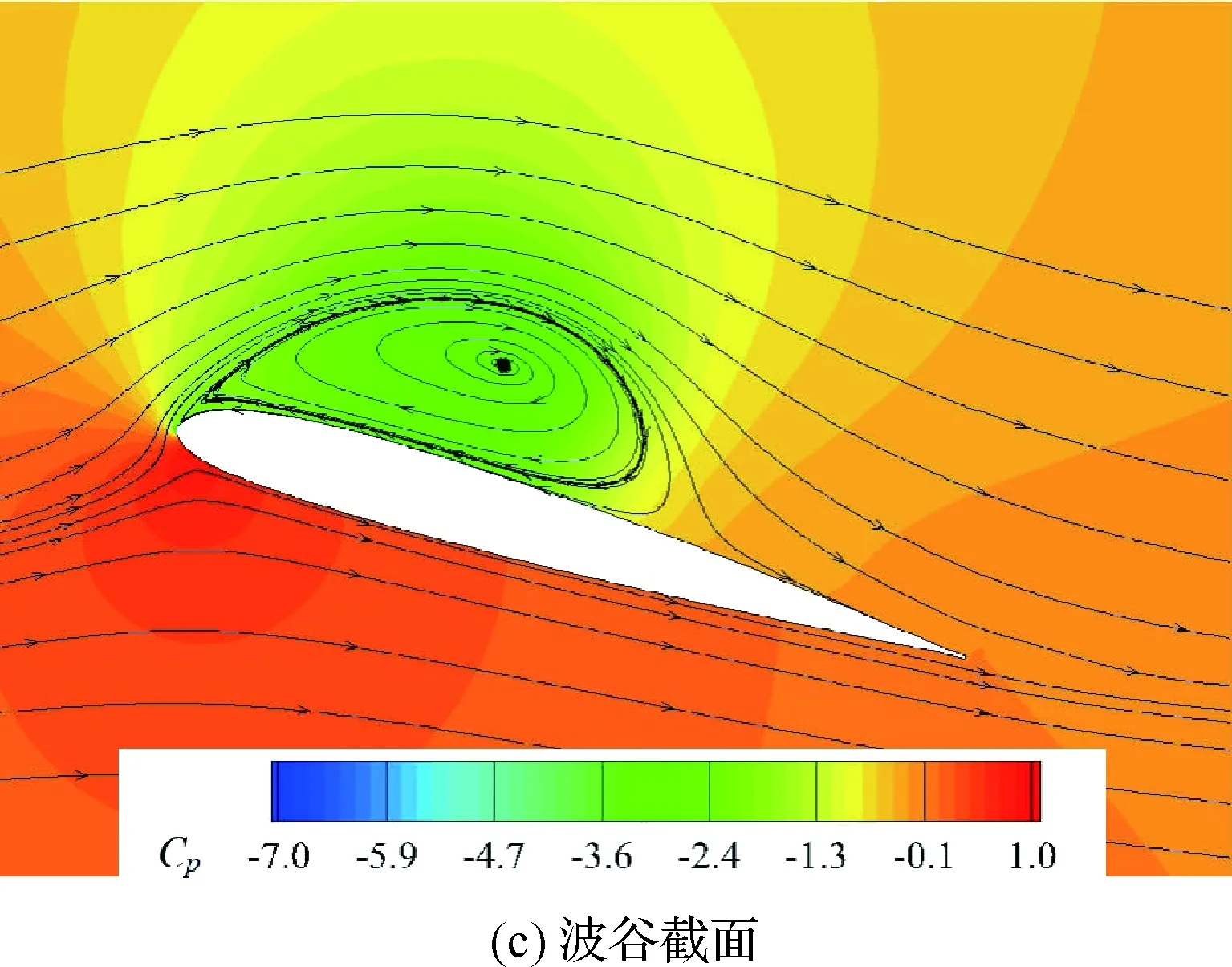
圖11 α=16.05°時不同截面的流場Fig.11 Flow fields on different sections at α=16.05°
迎角上仰至18.85°,Cp曲線及流場如圖12和圖13所示。原型翼CL接近峰值,分離渦幾乎覆蓋上表面,隨該渦向下游移動,低壓區后移,Cp峰值減小。與同處CL峰(α=16.05°)的A05W5流場相比,原型翼分離渦更強,所產生的低壓區造成更大的壓差阻力及俯仰力矩,同時也是CL峰高于A05W5的原因。A05W5此刻已經失速,主分離渦開始脫離上表面,低速回流區覆蓋了波谷截面和后半波峰截面。
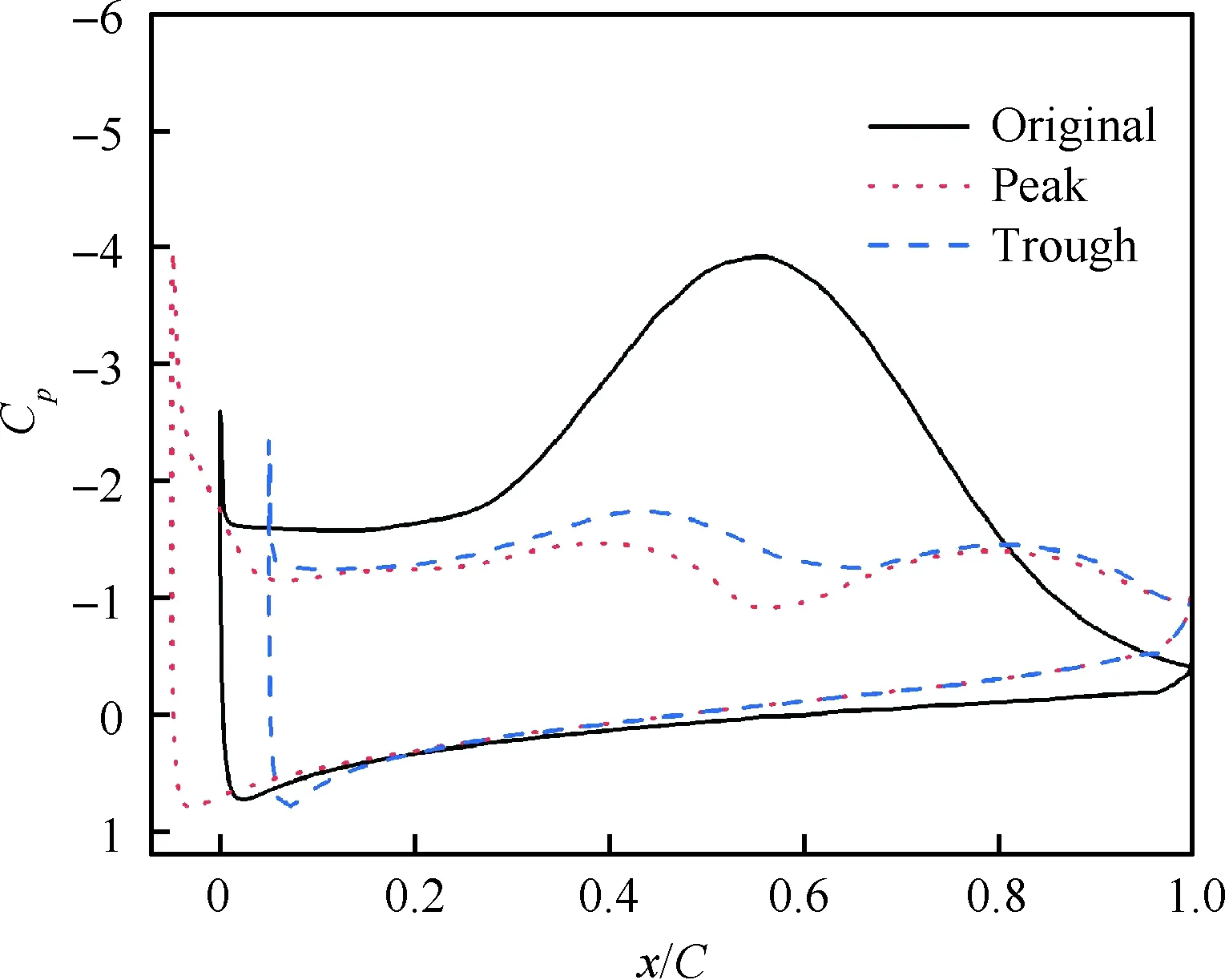
圖12 α=18.85°時不同截面的壓力系數Fig.12 Pressure coefficients on different sections atα=18.85°
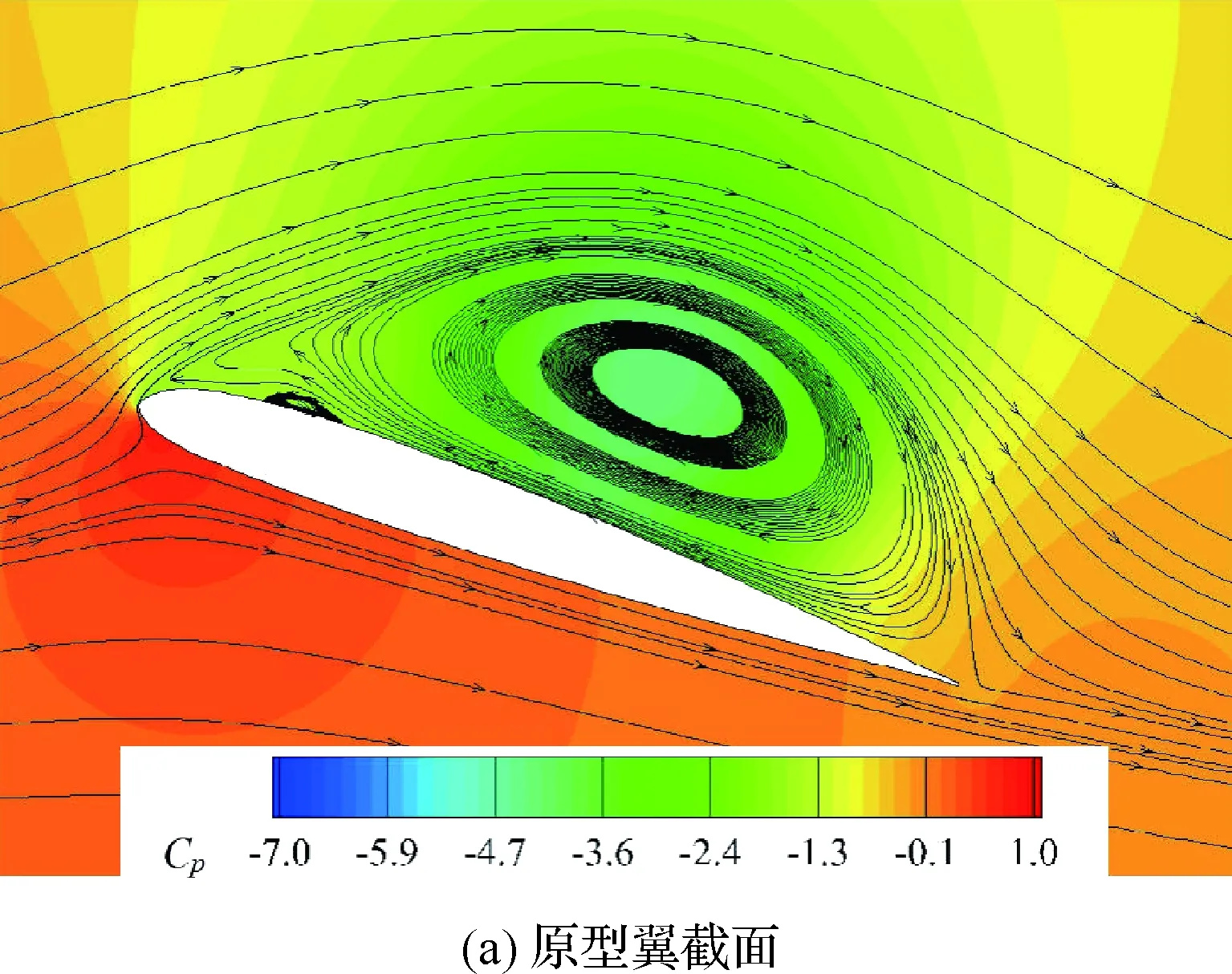
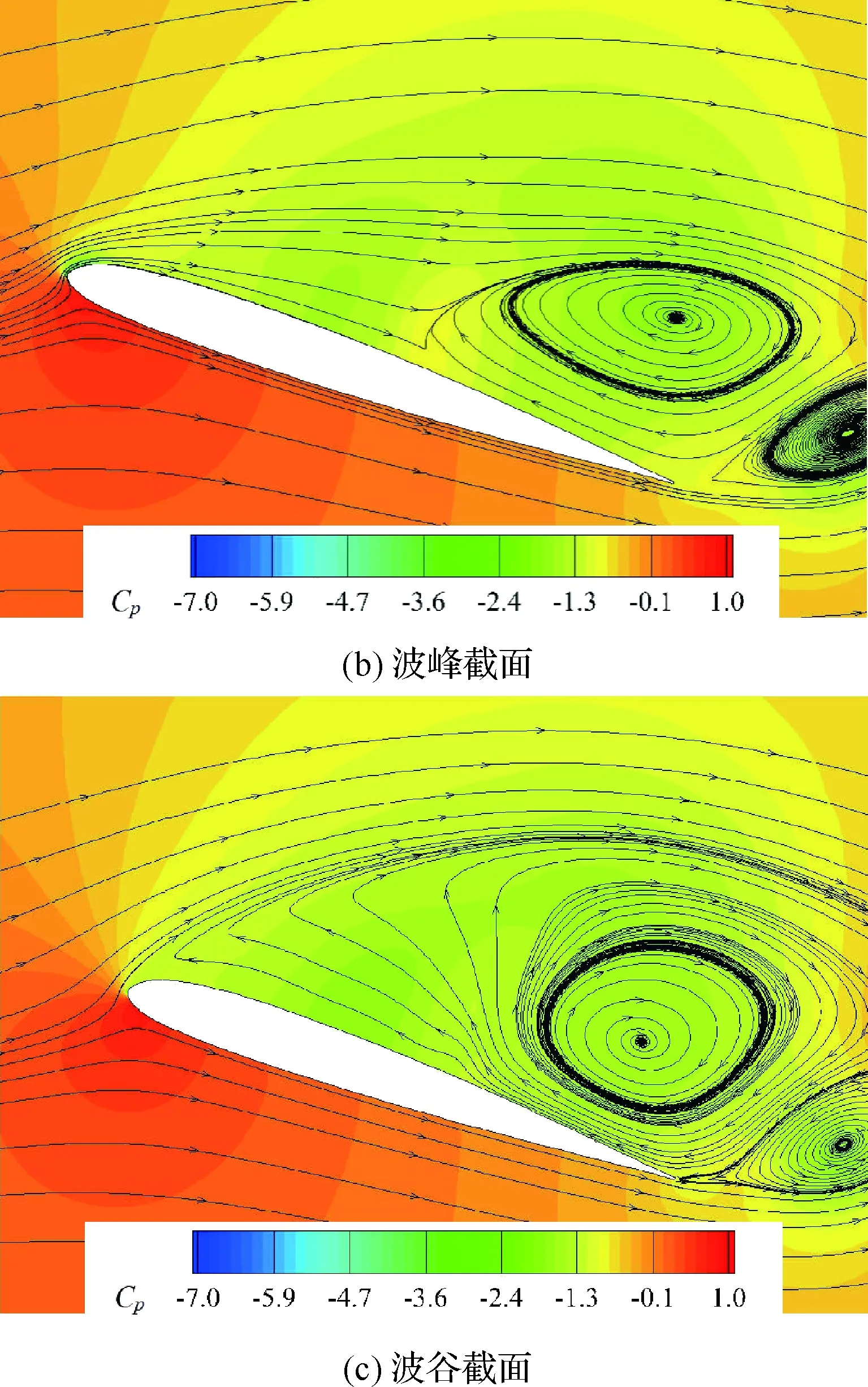
圖13 α=18.85°時不同截面的流場Fig.13 Flow fields on different sections at α=18.85°
圖14和圖15給出了最大迎角19.68°時的Cp曲線圖和流場。由于分離渦與其低壓區逐漸遠離以及渦誘導速度損失,原型翼CL驟降。同時分離渦在尾緣卷起的逆時針渦形成低壓區,導致低頭力矩高于A05W5,而A05W5尾緣渦此刻早已脫落(見圖15(b)和圖15(c))。即使在最大迎角,波峰截面前半區域仍然不存在分離渦,流動繼續附著在翼型表面,在一定程度上充當“翼刀”限制了分離渦展向傳播。另外,原型翼產生了二次前緣分離渦與逆時針渦結構,破壞了附著流,但這種反向渦對并未出現在仿生翼周圍。
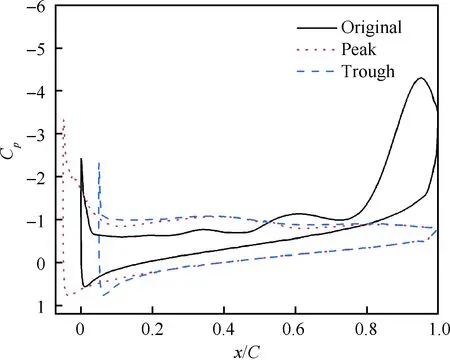
圖14 α=19.68°時不同截面的壓力系數Fig.14 Pressure coefficients on different sections atα=19.68°
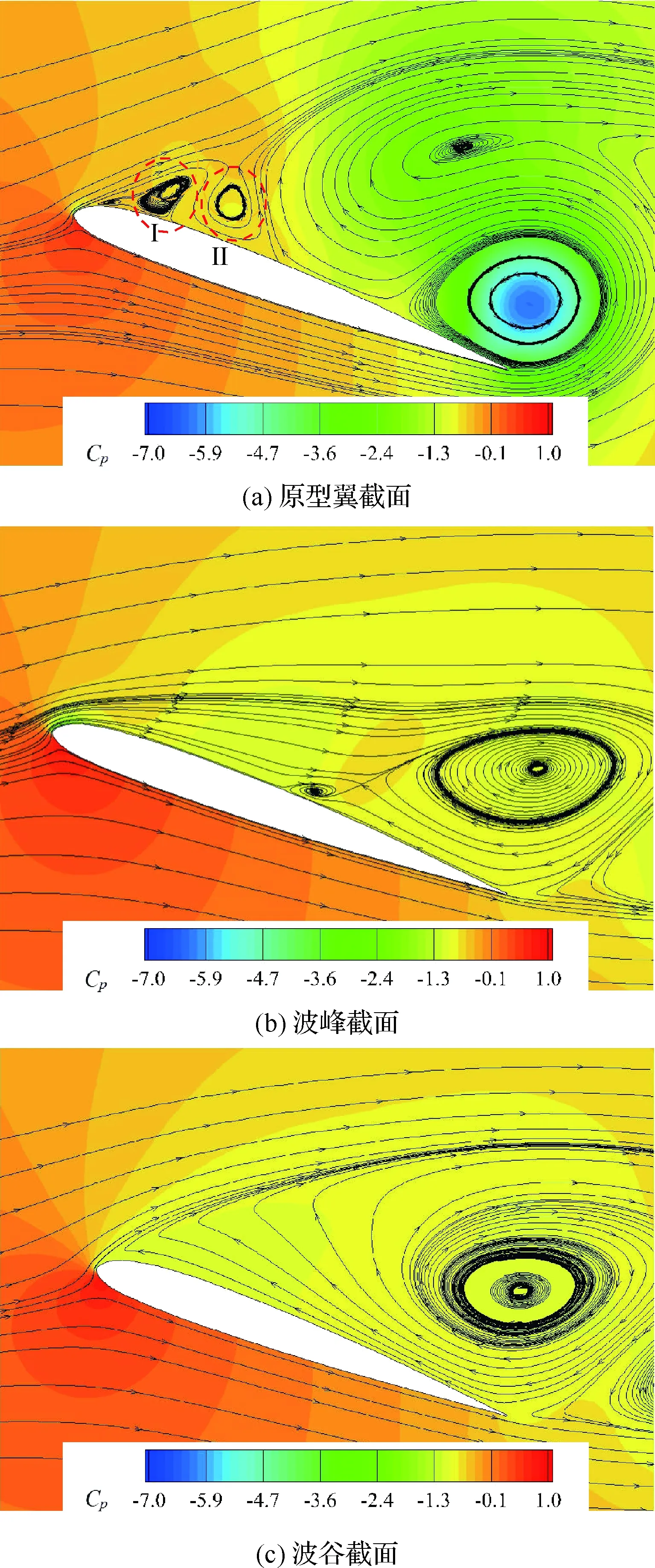
圖15 α=19.68°時不同截面的流場Fig.15 Flow fields on different sections at α=19.68°
隨后迎角開始下俯,兩種翼型的氣動系數呈現出不同變化趨勢。結合圖6看到原型翼的CL、CD和Cm都先回漲再驟降,而A05W5的氣動載荷始終平穩減小。圖16和圖17展示了迎角下俯到19.1°時的Cp曲線圖和流場。此刻原型翼CL回漲至高點。因為圖15(a)中的二次前緣分離渦Ⅰ向下游移動并增強,Cp峰值增加,升力增加,阻力和低頭力矩隨之增加。在圖15(a)中與該二次前緣渦成對出現的逆時針渦Ⅱ幾乎消散,從而看到渦Ⅰ與已經弱化的主分離渦連在一起(見圖17(a)),隨著迎角進一步減小,二次分離渦的脫落造成CL再次陡降。與之對比,A05W5并未出現二次分離渦的發展和脫落。
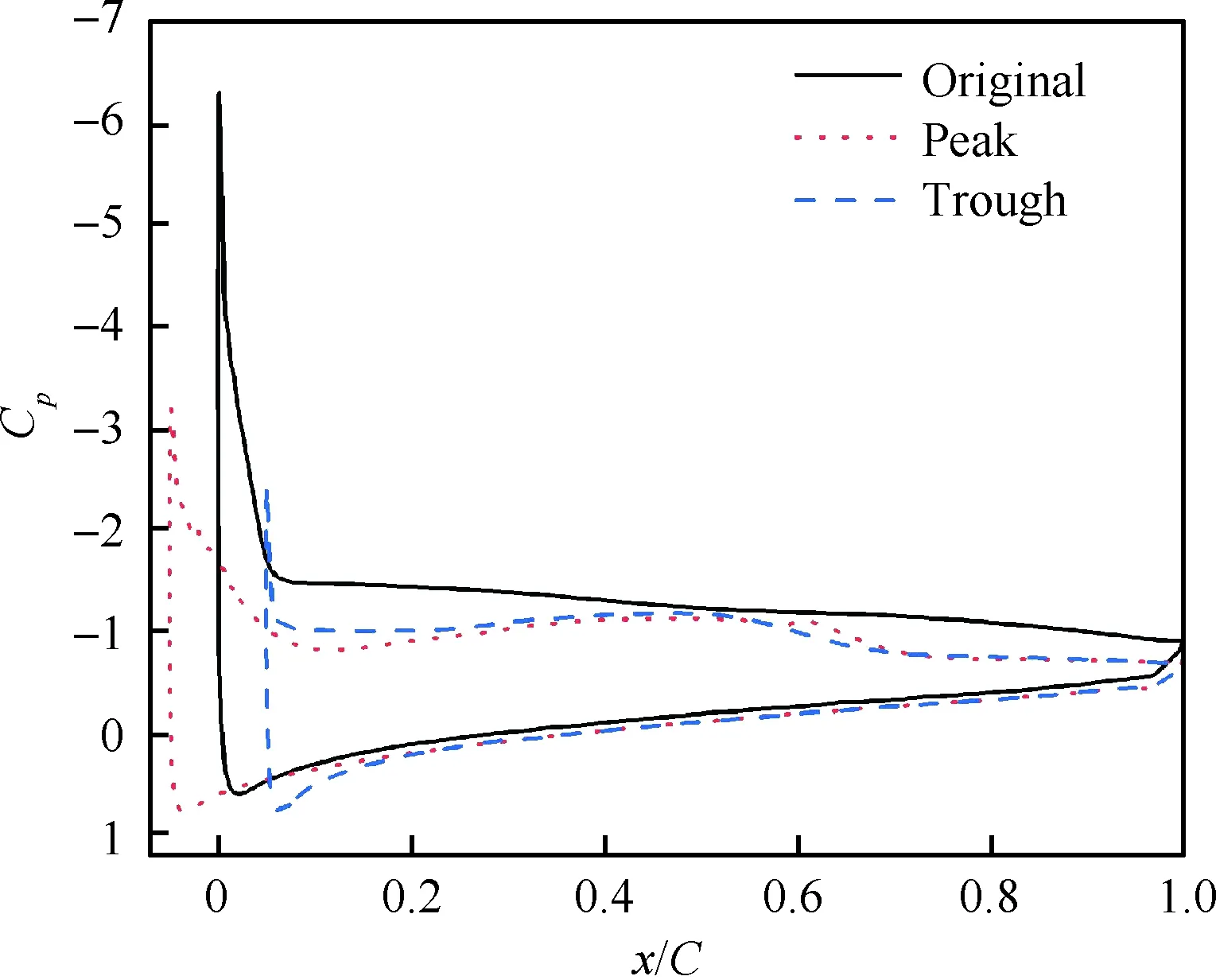
圖16 α=19.1°時不同截面的壓力系數Fig.16 Pressure coefficients on different sections atα=19.1°
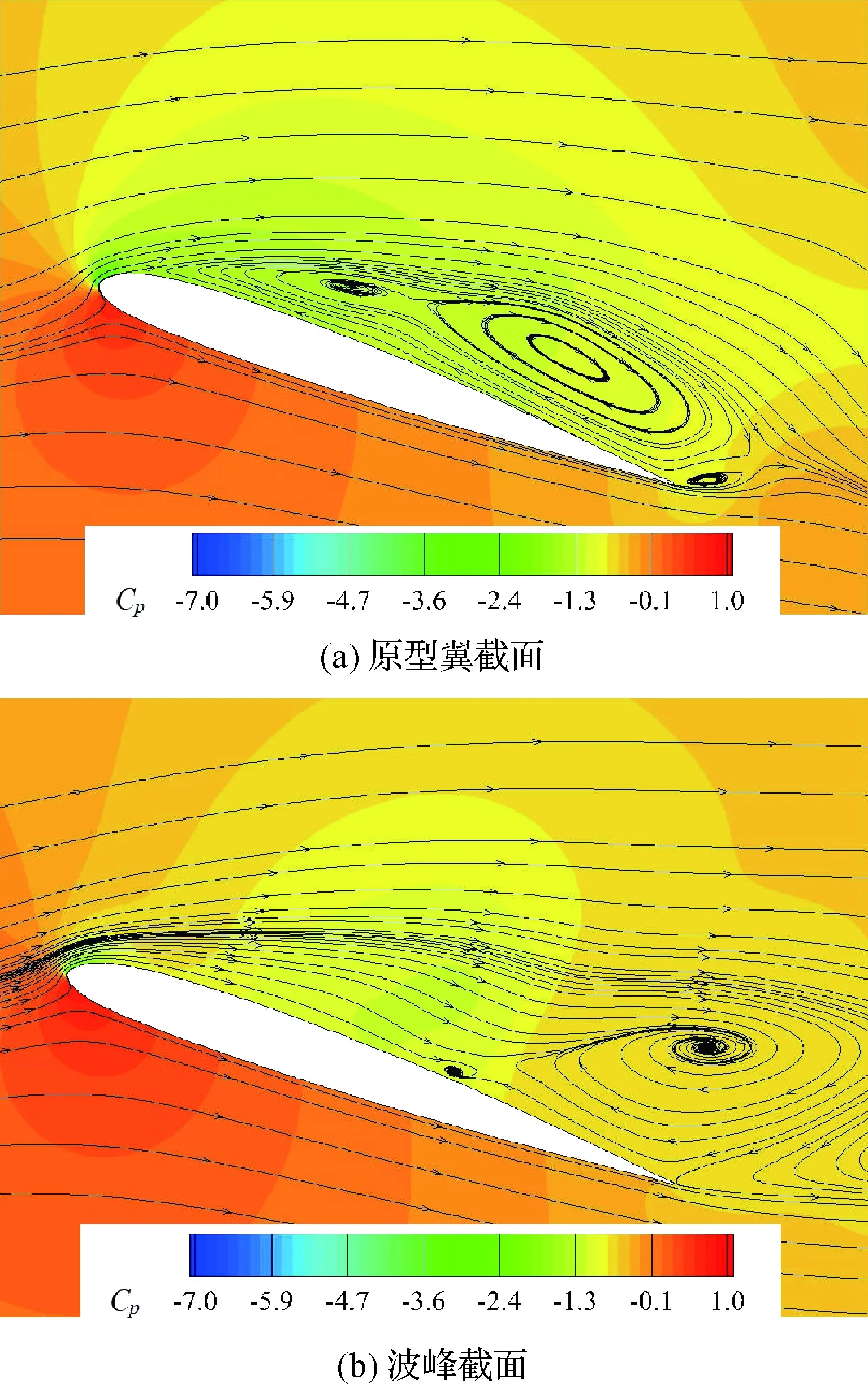
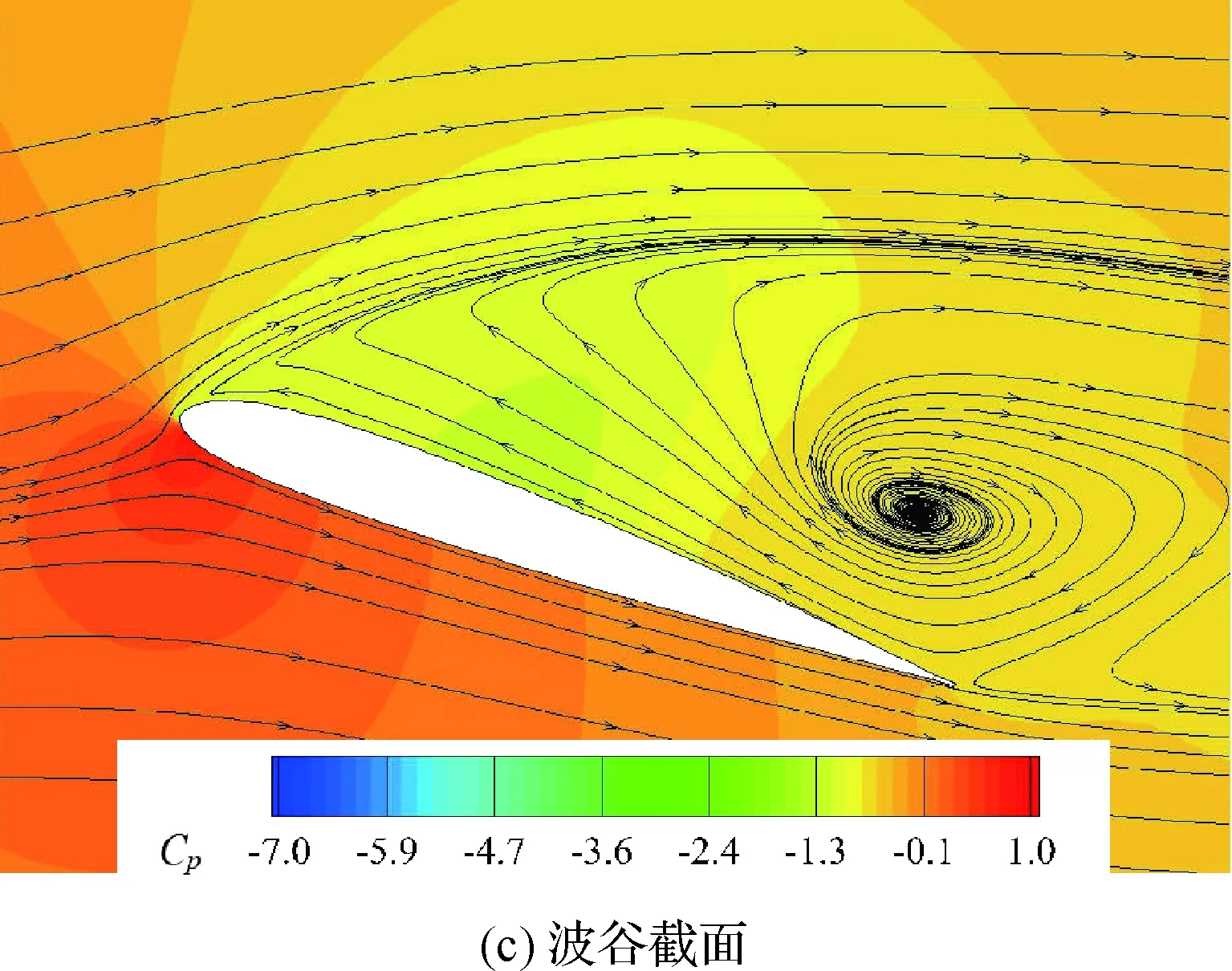
圖17 α=19.1°時不同截面的壓力系數Fig.17 Pressure coefficients on different sections atα=19.1°
綜上,仿生正弦前緣促使分離渦提前產生,但強度下降,盡管較弱的分離渦使得升力峰值有所損失,但顯著降低了阻力和俯仰力矩峰值,抑制了動態失速。同時仿生前緣抑制了二次分離渦的產生,使得下俯過程載荷變化平緩。前緣波峰越大或波長越小,上述趨勢越明顯。
3 運動參數與來流參數的影響
為了將仿生前緣應用于工程實踐,需要進一步探討其工作范圍。本文針對動態失速中最重要的運動參數(平均迎角、迎角振幅、折算頻率)以及來流參數(馬赫數),研究其對動態失速特性的影響以及仿生前緣在多種工況下的動態失速控制效果。采用仿生前緣翼A025W5與原型翼進行對比,參考工況為:α=10°+10°sin(ωt),k=0.1,Ma=0.3,Re=3.92×106。影響參數分析只改變所分析參數,其他參數和參考工況一致。
3.1 平均迎角
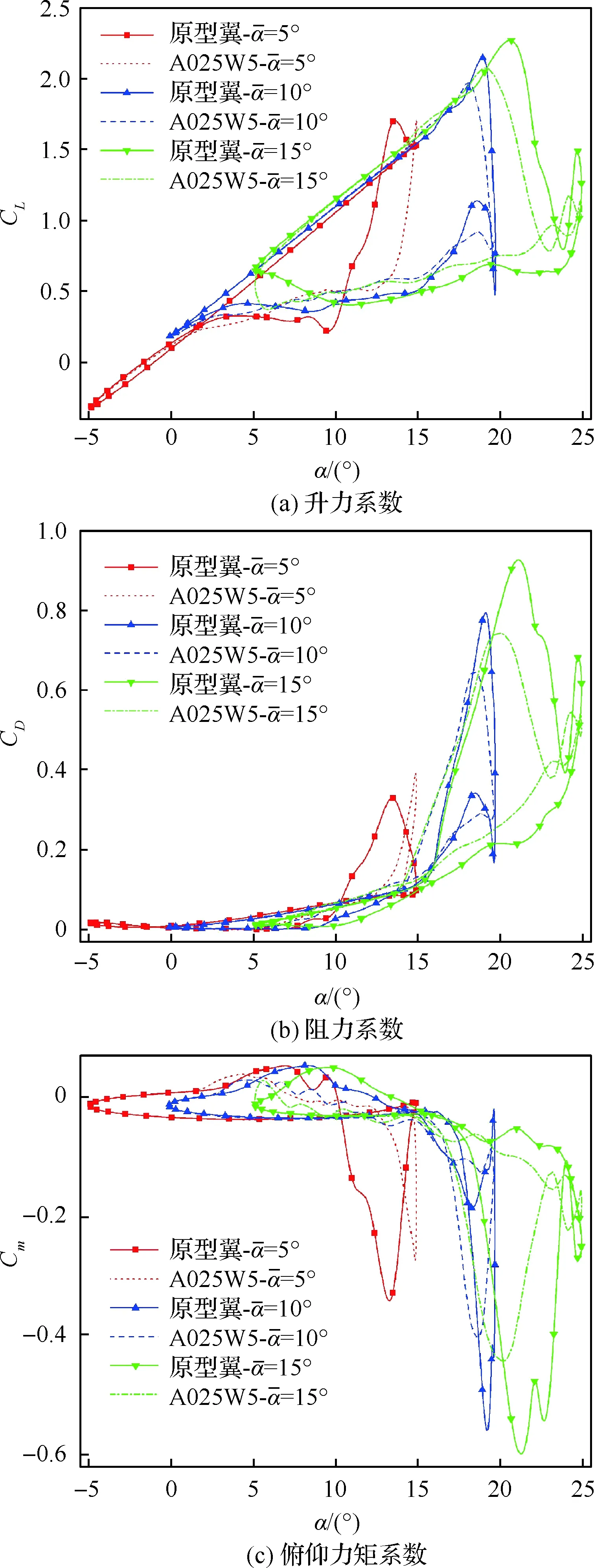
圖18 不同平均迎角下的氣動力系數Fig.18 Aerodynamic coefficients at different mean angles of attack
3.2 迎角振幅
圖19給出了迎角振幅(αm)分別為5°、10°、15°時原型翼和仿生翼的升力系數、阻力系數及俯仰力矩系數遲滯回線。隨著迎角振幅的增加,動態失速特性增強,各氣動系數遲滯效應更加明顯,反映在各氣動系數峰值增加以及流動再附現象推遲。在低迎角振幅情況下(αm=5°),載荷次波峰未出現,當迎角振幅增加,二次前緣分離渦加強從而產生載荷次波峰,仿生前緣能夠在一定程度上抑制二次分離渦與載荷次波峰的出現,緩和載荷變化。仿生前緣在3種迎角振幅下都能有效抑制俯仰力矩峰值,不同振幅下其減小量基本一致,升力峰值的損失也幾乎不受迎角振幅的影響,但阻力峰值的減小量在迎角振幅較小時(αm=5°)降低。
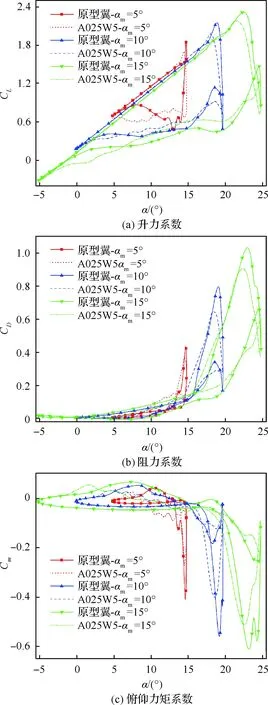
圖19 不同迎角振幅下的氣動力系數Fig.19 Aerodynamic coefficients at different amplitudes of angle of attack
3.3 折算頻率
前飛直升機旋翼的截面通常情況下的折算頻率在0.03~0.1之間,據此本文針對3種不同折算頻率(k=0.04、0.07、0.10)進行了動態失速模擬,升力系數、阻力系數和俯仰力矩系數的結果如圖20所示。首先,折算頻率的增加使得動態失速程度加深,遲滯環面積顯著增大,氣動載荷峰值及所對應迎角增加并且再附迎角減小。隨著折算頻率的增加,仿生前緣動態失速控制效果相對減弱,反映在俯仰力矩峰值的減小量和阻力峰值的減小量降低,盡管升力峰值損失也減小。另外,仿生翼型氣動載荷峰值的出現始終提前于原型翼,隨著折算頻率降低,這種提前效應愈發明顯。
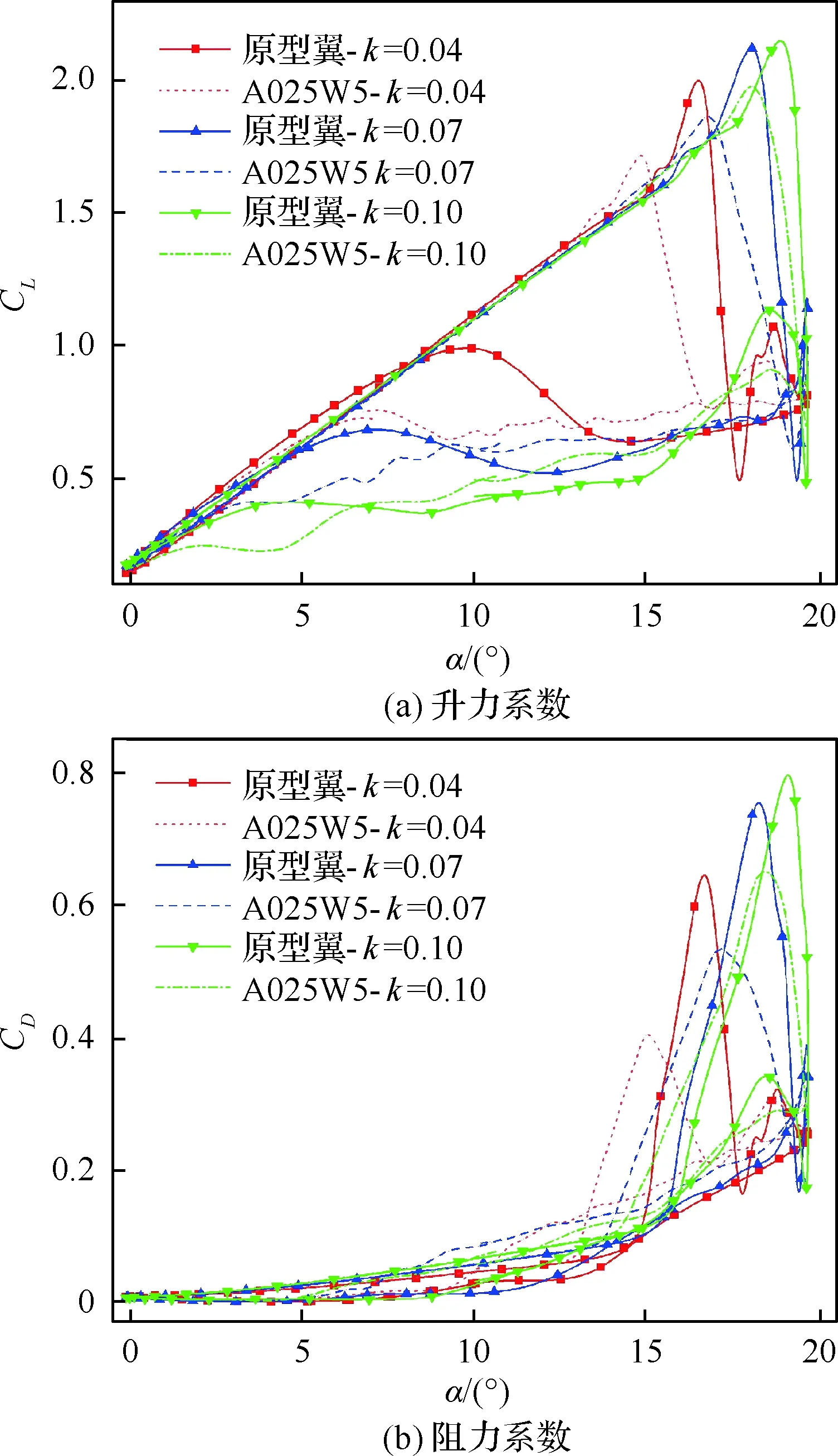
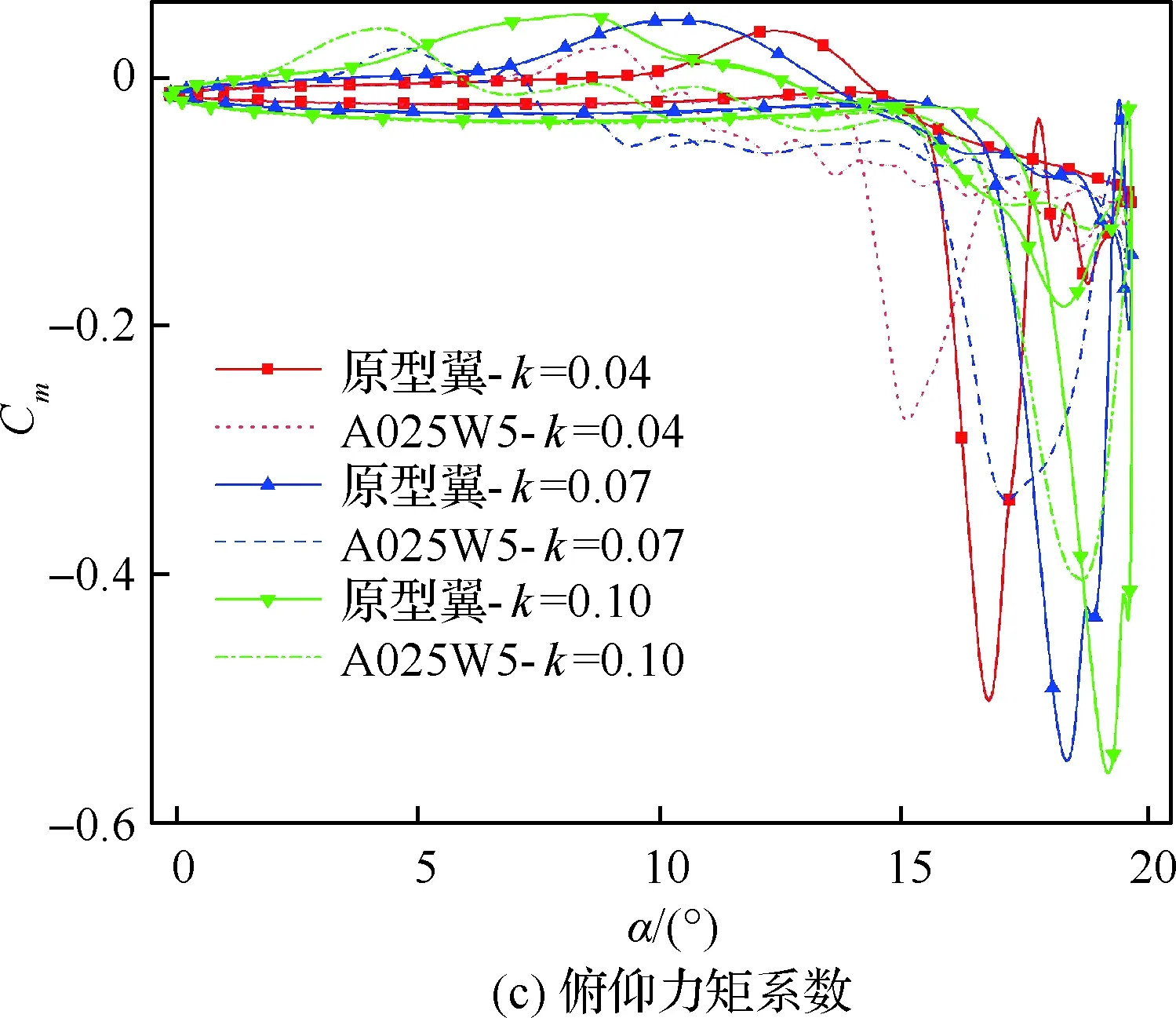
圖20 不同折算頻率下的氣動力系數Fig.20 Aerodynamic coefficients at different reduced frequencies
3.4 馬赫數
自由來流速度在直升機槳葉不同半徑處差異很大,為了探討來流速度對動態失速特性及仿生前緣動態失速控制的影響,本文計算了Ma分別為0.3、0.4和0.5下的原型翼和仿生翼的動態失速特性,結果如圖21所示。隨著來流速度增加,臨界逆壓梯度減小[25],前緣分離更易發生,導致前緣分離渦提前生成并向下游運動,又因為大來流速度下分離渦更容易耗散、脫落,因此渦強度減弱,氣動系數峰值減小。3種馬赫數下仿生前緣都能有效實現阻力峰值和低頭力矩峰值的抑制,隨著馬赫數增加,阻力峰值和俯仰力矩峰值的減小量先基本不變后降低,升力峰值損失也展現相同趨勢。
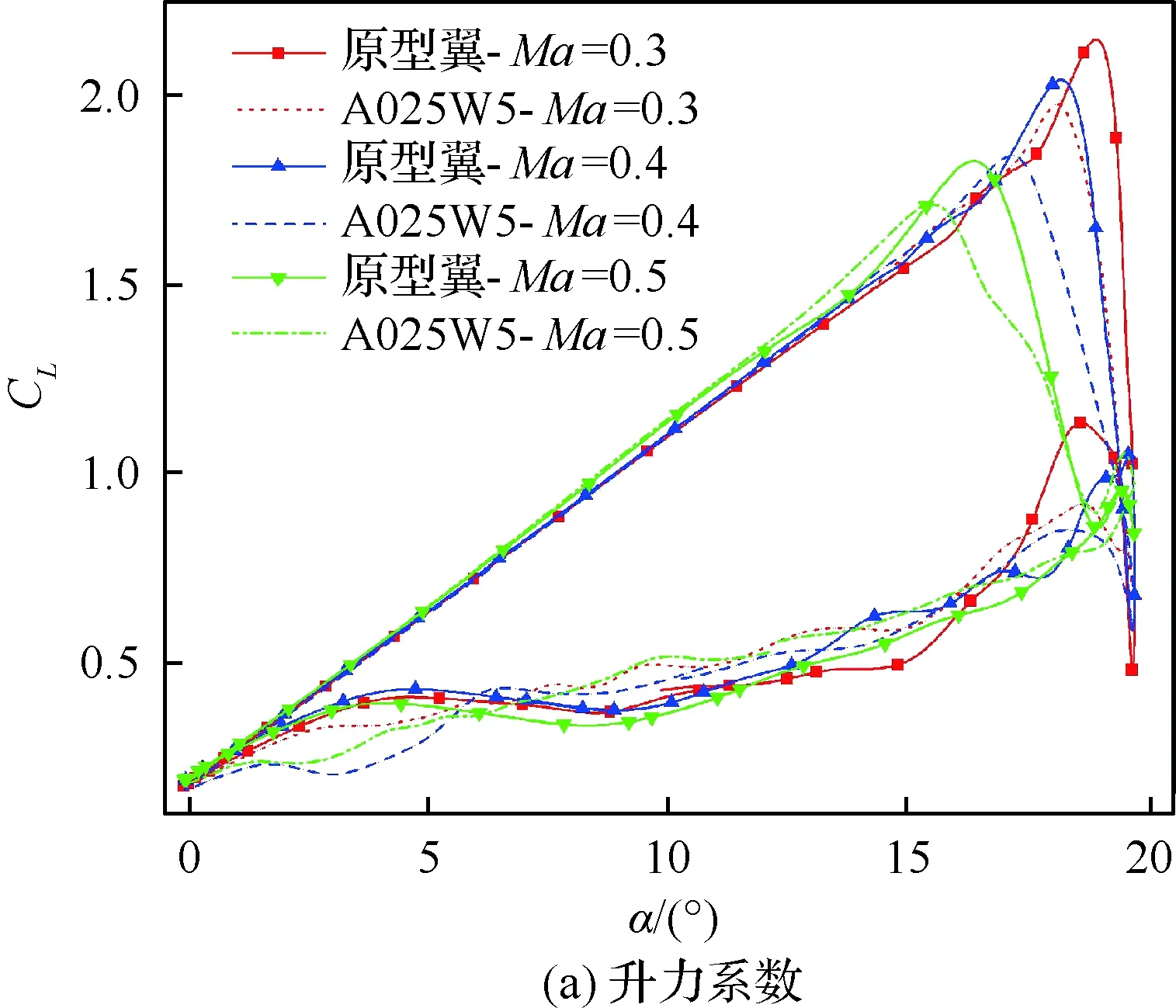
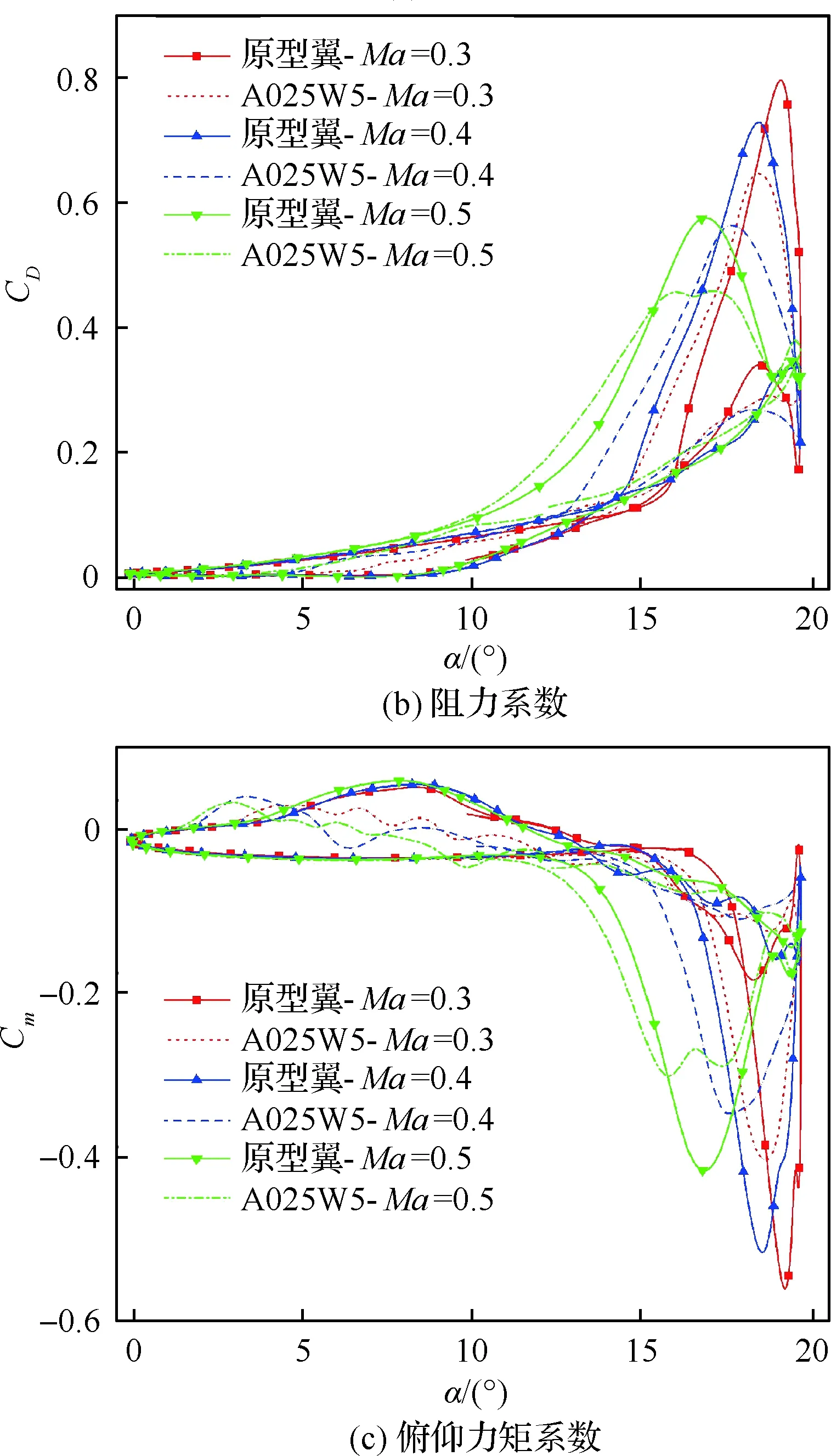
圖21 不同馬赫數下的氣動力系數Fig.21 Aerodynamic coefficients at different Mach numbers
4 結 論
1) 仿生前緣能夠顯著降低阻力峰值和俯仰力矩峰值,但最大升力系數有不同程度減小。當前緣波峰增加或波長減小,阻力峰值和俯仰力矩峰值減小量大幅增加,而升力峰值的減小量遠小于阻力和俯仰力矩峰值的減小量。
2) 前緣波谷的強逆壓梯度促使波谷提前分離并產生前緣渦,波峰截面前半上表面流動不受分離渦影響,始終附著在表面,起到了削弱波谷分離渦與限制其沿展向傳播的作用。同時,仿生前緣有效抑制了二次前緣渦,從而緩和了最大迎角附近的載荷變化。
3) 平均迎角、迎角振幅和折算頻率的增加都會加強動態失速遲滯特性,增加氣動系數峰值并推遲流動再附。當來流馬赫數增加時,氣動系數峰值與其對應迎角都減小。
4) 平均迎角越大,仿生翼型的阻力和俯仰力矩的抑制程度增加,升力峰值損失輕微增加;迎角振幅對仿生前緣的動態失速控制效果影響較小;折算頻率增加,仿生翼各載荷峰值減小量均降低,載荷峰值所對應迎角的提前量減小;隨著來流馬赫數增加,仿生翼的各載荷峰值減小量先基本不變后降低。

