關注課標四基 提高命題質量

李初興

[摘要]基于課程標準中的“四基”，為提高試題質量，教師應結合小學數學的相關知識點，把握設計試題的兩大方向——既要關注知識的過程性和理解性，又要關注知識的難度和靈活度，讓試題能真實地反映出學生的數學學習過程和結果。

[關鍵詞]蘇教版;紙筆測驗;課程標準;優化

[中圖分類號]G623.5??[文獻標識碼]A??[文章編號]1007-9068（2020）02-0047-02

《義務教育數學課程標準（2011年版）》指出：“要建立目標多元、方法多樣的評價體系，評價既要關注學生學習的結果，也要重視學習的過程;既要關注學生數學學習的水平，也要重視學生在數學活動中所表現出來的情感與態度，幫助學生認識自我、建立信心。”然而，現有的紙筆測驗中存在著少量的難題、怪題，不僅在解題過程中浪費了學生的大量思考時間，還打擊了學生學習數學的興趣。

實際上，教師在編制試題時，要圍繞課程標準提出的基礎知識、基本技能、基本思想方法、基本活動經驗等“四基”來檢測學生對知識的掌握情況，真實地反映出他們的學習過程和學習結果。

一、試題要關注知識的過程性和理解性

學生學習數學知識首先要掌握基礎知識，學有余力的學生還可以挑戰一些難題。因此，試題的編寫首先要關注基本知識和基本技能，再去考慮基本數學思想方法和基本活動經驗。在考查基本知識和基本技能時，雖然是靜態的紙筆測驗，但也要融入考查學生對知識過程性和理解性的掌握程度，而不僅僅是考查學生死記硬背的數學知識。

例如，在教學蘇教版六年級上冊第三單元“分數除法”時，我保留了課程原來的識別記憶要求，還要求學生能夠理解整數除以分數、分數除以分數的算理和算法。

【優化前】計算：（1）??????（2）

【優化后】（1）先計算，再用畫圖或文字等方式表示出這道題的計算過程和結果。

（2）先計算，再用畫圖或文字等方式表示出這道題的計算過程和結果。

這兩道分數除法計算題，如果像“優化前”這樣設計題目，那么大部分學生就都懂得整數（或分數）除以分數可以轉化為乘法來計算，等于整數（或分數）乘這個分數的倒數。得益于平時的強化訓練結果，學生會條件反射地快速完成，并且正確率極高。如果像“優化后”這樣設計題目，旨在考查學生對分數除法計算方法的過程性理解時，有些學生就會無從下手，這也體現出平時教師的課堂教學情況和學生對該題的真正理解水平。

又如，在教學蘇教版四年級下冊第七單元“三角形的特性”時，為了考查學生對三角形穩定性的理解，我在編寫試題時去除了以往學生熟悉的題型。

【優化前】選擇題：下面哪個圖形具有穩定性？（）

A.三角形??B.梯形??C.平行四邊形??D.長方形

【優化后】選擇題：有兩個三角形，它們三邊的長度分別是4厘米、5厘米、6厘米，關于這兩個三角形說法正確的是（）。

A.兩個三角形的形狀相同且面積相同

B.兩個三角形的形狀相同但面積不同

C.兩個三角形的形狀不同但面積相同

D.兩個三角形的形狀和面積都不同

這兩道題都是在考查學生對三角形穩定性的記憶情況，雖然都是選擇題，但是“優化前”的題目屬于記憶型的，學生只要記住“三角形具有穩定性”這一結論即可，無須去回憶三角形穩定性由來的驗證過程;“優化后”的題目屬于理解型的，要求學生在理解題目信息的基礎上提煉出三角形具有穩定性這一特征。

二、試題要關注知識的難度和靈活度

世界上的萬事萬物都不相同，每個學生對數學的認識也不相同。教師在編制數學題時應該從基礎入手，讓每個學生都能完成其中一部分，同時兼顧難度和靈活度，讓學有余力的學生發揮出他們實能力。

例如，在教學蘇教版四年級上冊第七單元“整數四則混合運算”時，教材的重難點是要求學生熟練掌握整數四則混合運算的運算順序，并正確計算。

【優化前】遞等式計算：

（1）300-（120+25x4）????（2）（600+10+120）÷6

【優化后】算“24點”：用3、4、5、6這四個數和運算符號（加、減、乘、除、括號等）計算出24，可以這樣算（），也可以這樣算（）。（括號里寫算式，每寫出一個算式得1分，滿分10分）

對比優化前后的兩道題目，“優化后”的題目不僅要求學生能完成基礎的計算，還要求學生能運用計算這項工具創造性地去探究和解決更多的新問題，形成新的數學活動經驗。這就要求學生在平時的學習過程中能舉一反三，拓寬學習視野，多面對嶄新的問題情境，逐漸形成靈活多變的數學思維方式。

又如，在教學蘇教版六年級上冊第六單元“百分數”時，教材中的解決問題是單一型的生活情境，為了幫助學生感受到真實的生活氛圍，我在編制試題時選擇了綜合的生活情境，使學生在完成練習中學會比較和選擇。

【優化前】一個街心花園占地公頃，其中草坪占，花圃占，其余是人行道。

（1）草坪和花圃的面積一共是多少公頃？

（2）草坪的面積比花圃大多少公頃？

（3）人行道的面積是多少公頃？

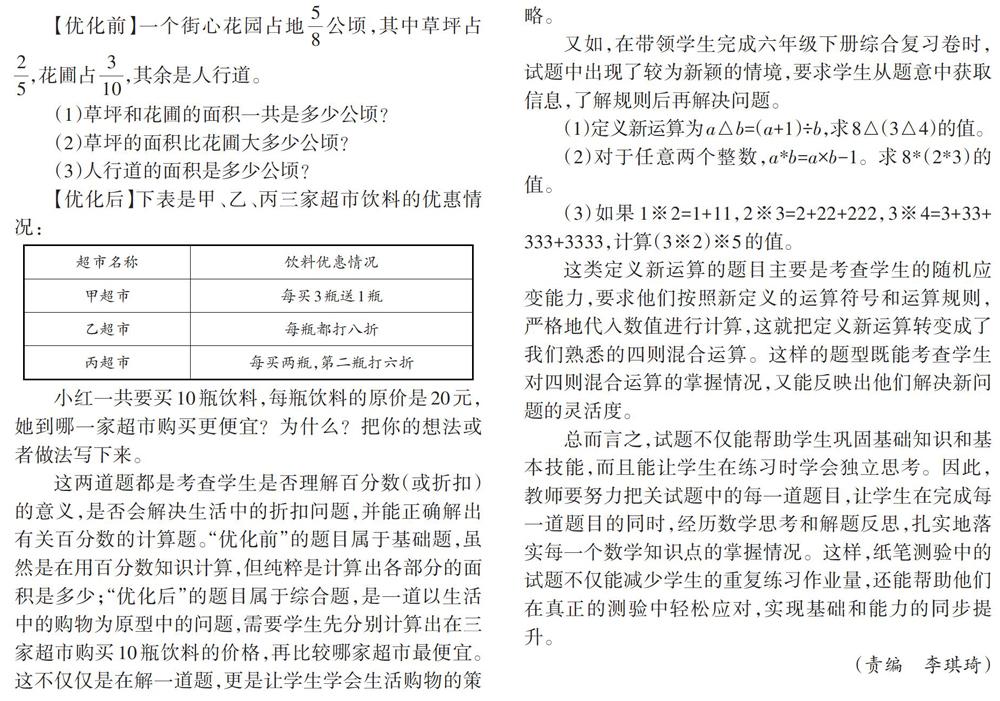
【優化后】下表是甲、乙、丙三家超市飲料的優惠情況：

小紅一共要買10瓶飲料，每瓶飲料的原價是20元，她到哪一家超市購買更便宜？為什么？把你的想法或者做法寫下來。

這兩道題都是考查學生是否理解百分數（或折扣）的意義，是否會解決生活中的折扣問題，并能正確解出有關百分數的計算題。“優化前”的題目屬于基礎題，雖然是在用百分數知識計算，但純粹是計算出各部分的面積是多少;“優化后”的題目屬于綜合題，是一道以生活中的購物為原型中的問題，需要學生先分別計算出在三家超市購買10瓶飲料的價格，再比較哪家超市最便宜。這不僅僅是在解一道題，更是讓學生學會生活購物的策略。

又如，在帶領學生完成六年級下冊綜合復習卷時，試題中出現了較為新穎的情境，要求學生從題意中獲取信息，了解規則后再解決問題。

（1）定義新運算為a△b=（a+1）÷b，求8△（3△4）的值。

（2）對于任意兩個整數，a*b=axb-1。求8*（2*3）的值。

（3）如果1※2=1+11，2※3=2+22+222，3※4=3+33+333+3333，計算（3※2）※5的值。

這類定義新運算的題目主要是考查學生的隨機應變能力，要求他們按照新定義的運算符號和運算規則，嚴格地代入數值進行計算，這就把定義新運算轉變成了我們熟悉的四則混合運算。這樣的題型既能考查學生對四則混合運算的掌握情況，又能反映出他們解決新問題的靈活度。

總而言之，試題不僅能幫助學生鞏固基礎知識和基本技能，而且能讓學生在練習時學會獨立思考。因此，教師要努力把關試題中的每一道題目，讓學生在完成每一道題目的同時，經歷數學思考和解題反思，扎實地落實每一個數學知識點的掌握情況。這樣，紙筆測驗中的試題不僅能減少學生的重復練習作業量，還能幫助他們在真正的測驗中輕松應對，實現基礎和能力的同步提升。