強化自我反思
——談“矛盾沖突”對初中數學課堂教學的影響

馬 龍

（甘肅省隴南市成縣城關中學，甘肅隴南 742500）

引 言

數學知識具有獨特的魅力，此種魅力可以通過矛盾沖突有效地激發出來。合理的矛盾沖突，可以充分調動初中生的學習欲望和興趣，使學生學會正視自我，進行深入反思和思考，了解自身的學習情況。《論語》中說：“吾日三省吾身”，也是這個道理。矛盾沖突的科學應用，賦予了數學教學新的魅力和內涵，對學生自信心的引導有著很大的幫助，使學生體驗到滿足感。

矛盾沖突在初中數學課堂教學中主要分為兩大類，即知識引入矛盾沖突和新知識探究矛盾沖突。

一、合理引入矛盾沖突，能夠調動學生的自主學習性

數學教學注重對學生的思維引導，通過思索和探究拓寬學生視野，使學生從多方面接觸數學知識，并進行合理應用。只有教育道路上經歷艱難之路，才能培養學生聰穎、好學、上進。教育理論也要求在培養學生能力的同時，須培養學生的探究心理，使其善于發現身邊事物并進行深入研究，通過知識學習構建精神世界。數學課堂教學內容的設計，對于教學水平的提升有很大的影響，對學生探究方向的引導也發揮著一定的作用。教師應設置教學引入環節，將學生在學習中遇到的困惑以及誘發的矛盾沖突帶入教學，營造自我探究的環境，讓學生在豐富的知識海洋中徜徉和探索，感受科學的魅力，自主學習能力也會得到很大提升[1]。

二、探究教學中引入矛盾沖突，能夠激發學生的學習潛能

問題導入和訓練是學生學習數學知識的基礎。在初中數學教學知識導入過程中，會與舊知識發生一定的矛盾沖突。學生在理解數學知識時會形成矛盾意識，此時在探究式教學中引入矛盾沖突，可以引導學生形成較為完整的知識體系。很多數學知識看似有一定的邏輯關系，但學習起來又不太符合邏輯判斷思維，從而使學生在思考時存在一定的困惑，在認知過程中又形成矛盾沖突。數學教師即可以利用知識矛盾點，引導學生自主探究[2]。

矛盾沖突的設置，需要數學教師提前設計好內容，做好課前準備，合理掌控課堂節奏，使各教學環節層層遞進，把握每一個教學環節，使學生在矛盾沖突發生時能夠從容應對，并合理利用矛盾沖突帶來的探究機會以提升學生的綜合能力和素養。

例如，勾股定理相關知識教學中，教師如直接向學生講解勾股定理的概念，學生很容易感到困惑，甚至產生疑慮。此時，教師可設置合理的矛盾沖突，如圖1所示：用幾個小方塊拼接成正方形，圖中兩個標黑色的三角形可以拼接成一個正方形，教師可以結合教學知識引入勾股定理知識，即直角三角形兩個直角邊平方的和與斜邊平方的數值相等，用a、b表示兩個直角邊，c表示斜邊，則可以了解勾股定理的公式為a2+b2=c2。通過矛盾沖突的設定，來引導學生掌握勾股定理知識[3]。

圖1

三、合理利用矛盾沖突理論，拓展學生的思考范圍

初中生在學習數學知識過程中，經常會遇到“簡”和“繁”的矛盾沖突。對于同一問題，學生可以從不同的角度進行思考，找到解答問題的不同方法。有的方法比較直觀快速，有的方法比較繞彎，其產生的效果也會有所不同。有些學生直接找到最簡單的方法，有些學生經過繁雜的推算找到解答方法。簡單與復雜的方式，對于初中生來講都是收獲知識的過程。在此過程中，學生思維方式發生了一定改變，開闊了視野，對知識的理解從表面到內部逐漸深入，經過研究和總結，可以找到最優、最快速的解題方式。

例如，開展幾何圖形相關知識教學中，教師應引導學生對抽象知識進行深入理解，全面掌握圖形性質、概念，并與其他知識相結合，使學生的基本知識技能有所提升，從而對數學知識有更加深入的理解，通過透視圖形，拓展知識面。

例如，證明三角形內角和定理過程。

方法1：如圖2所示，△ABC中，延長BC至點D，經過點C做CE，使EC平行于AB。由于同位角相等，則∠B與∠ECD相等，且根據內錯角相等，則∠A與∠ACE相等。因此，可以得出∠ACB+∠ECD+∠ACE為180°，將角進行替換可得出∠ACB+∠A+∠B為180°，通過以上推算得出三角形三個內角之和為180°。

圖2

方法2：如圖3所示，△ABC中，過點C作直線BA的平行線CD，結合內錯角相等定律，可以了解到∠A與∠1相等。由于CD平行于BA，則∠B+∠1+∠ACB等于180°。由此可以推算出∠A+∠B+∠ACB等于180°。

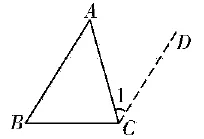
圖3

通過以上研究可知：三角形內角度數證明可以有多個推算方法，其不僅可以利用平行線作為輔助進行推算，還可以通過繪制外接圓的方式進行推算和證明。多樣化的推算方法以基礎數學知識為核心，圍繞知識定律和特點開展推導式學習。使學生通過多樣化的推算，可以了解三角形內角的基本性質特點，并掌握其特點的推算方法，從而激發學生學習數學知識的興趣，感受數學知識的神奇。除此之外，學生在證明過程中，也可以穿插應用多個數學知識，充分體現知識的互通性，從而加強知識的綜合性，進一步鞏固知識，拓展解題思路，探索新的學習方式。

結 語

綜上所述，教師開展數學課堂教學時合理應用矛盾沖突的方式，可以引導學生學會自我探究，提升獨立學習能力，并使數學課堂氛圍更加活躍、輕松，賦予數學課堂以更多的活力。學生也可以通過對知識點的探究，了解自己學習中存在的不足，走出學習的誤區，拓展思維方式，學會正確對待矛盾沖突，并通過問題解答，使思維得到碰撞，引導學生全身心地投入數學學習，加強多樣化的學習體驗，從而滿足學生對知識的需求，挖掘內在潛力，以感受數學的學習魅力。