雙基地噪聲雷達(dá)中直達(dá)波干擾抑制技術(shù)研究

魯振興，尹 偉，洪永彬

(中國(guó)電子科技集團(tuán)公司第五十四研究所，河北 石家莊 050081)

0 引言

由于具有優(yōu)良的低截獲概率特性以及無(wú)距離模糊特性，從20世紀(jì)90年代后期開始，噪聲雷達(dá)技術(shù)逐漸引起了人們的研究興趣[1-3]，并得到了快速發(fā)展。

噪聲雷達(dá)多采用連續(xù)波體制，雙基地噪聲雷達(dá)的發(fā)射站和接收站間隔一定距離以減小直達(dá)波及雜波強(qiáng)度。由于直達(dá)波和多徑雜波與目標(biāo)回波在時(shí)域上無(wú)法分開。在噪聲信號(hào)的相關(guān)處理中，旁瓣(噪聲基底)效應(yīng)非常明顯[4]，這會(huì)造成弱目標(biāo)被直達(dá)波、雜波和強(qiáng)目標(biāo)旁瓣淹沒(méi)的現(xiàn)象，從而嚴(yán)重影響系統(tǒng)的作用距離。在實(shí)際中，直達(dá)波和雜波的抑制非常關(guān)鍵，必須采取多種措施(包括物理措施、空域以及時(shí)域處理等)降低直達(dá)波和雜波對(duì)微弱目標(biāo)檢測(cè)的影響。由于物理隔離和空域?yàn)V波的抑制能力有限，自適應(yīng)時(shí)域?qū)ο蔀橹边_(dá)波和雜波干擾抑制的一種必備措施。

常用的自適應(yīng)時(shí)域?qū)ο惴ò↙MS算法、遞歸最小二乘(RLS)算法以及相應(yīng)的改進(jìn)形式。由于RLS算法的計(jì)算復(fù)雜度很高，實(shí)際應(yīng)用較少。

LMS算法中，步長(zhǎng)參數(shù)越大，收斂速度越快，穩(wěn)態(tài)誤差也越大[5-6]。其收斂速度與穩(wěn)態(tài)誤差始終是矛盾的。然而，在直達(dá)波和雜波的對(duì)消應(yīng)用中即使對(duì)于較大的步長(zhǎng)參數(shù)，算法收斂后得到的對(duì)消比與維納濾波方法相差也不大。因此，減小步長(zhǎng)對(duì)對(duì)消比的改善有限[7]。Malanowski[8]曾比較了不同自適應(yīng)算法在直達(dá)波和雜波對(duì)消中的效果，表明變步長(zhǎng)LMS算法沒(méi)有明顯的優(yōu)勢(shì)。

噪聲雷達(dá)中，參考信號(hào)相鄰采樣點(diǎn)之間存在明顯相關(guān)性，其自相關(guān)矩陣的特征值散度[7]很大，從而造成LMS算法的收斂速度變慢。基于聯(lián)合過(guò)程估計(jì)的干擾抑制算法在LMS濾波之前，對(duì)輸入信號(hào)進(jìn)行去相關(guān)處理，從而可以提高算法的收斂速度[9]。

本文通過(guò)理論分析，對(duì)雙基地噪聲雷達(dá)中基于LMS的直達(dá)波干擾抑制算法收斂特性進(jìn)行研究，給出了對(duì)消剩余的收斂曲線。提出基于聯(lián)合過(guò)程估計(jì)的干擾抑制算法，通過(guò)對(duì)輸入信號(hào)去相關(guān)處理提高了算法的收斂速度。

1 基于LMS的自適應(yīng)干擾抑制方法

1.1 信號(hào)模型

假設(shè)強(qiáng)多徑雜波存在于前M個(gè)距離單元之內(nèi)，那么回波通道的接收信號(hào)可以表示為：

(1)

式中，Sd(t)=adSr(t)為直達(dá)波信號(hào)；ad為直達(dá)波信號(hào)的復(fù)幅度；Sr(t)為接收參考信號(hào)；Sci(t)=aciSr(t-τci)為第i個(gè)距離單元的雜波信號(hào)；aci為該雜波信號(hào)的復(fù)幅度；τci為其相對(duì)參考信號(hào)的延遲；Stnc(t)則包含了目標(biāo)回波、接收機(jī)噪聲以及遠(yuǎn)距弱雜波，并且假設(shè)目標(biāo)位于強(qiáng)雜波區(qū)之外，即目標(biāo)延遲τt>τcP。

直達(dá)波和雜波均可表示為延遲后的參考信號(hào)，于是，可以將直達(dá)波和雜波用統(tǒng)一的符號(hào)進(jìn)行表示：

(2)

式中，

1.2 算法原理

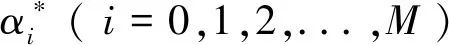
J=E[|e(n)|2]=

(3)

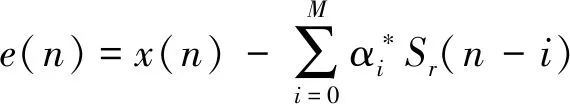
LMS算法利用瞬時(shí)梯度對(duì)權(quán)向量進(jìn)行調(diào)整。假設(shè)在n時(shí)刻濾波器的權(quán)向量為α(n)，那么對(duì)梯度J(n)的瞬時(shí)估計(jì)為：

(4)

LMS算法對(duì)加權(quán)向量的調(diào)整方法為：

α(n)+μSr(n)e*(n)，

(5)

式中，μ為迭代步長(zhǎng)。在算法初始時(shí)刻濾波器系數(shù)α(0)可以設(shè)置為某些先驗(yàn)值也可以設(shè)置為0。

根據(jù)Butterweck的波理論[10]，LMS算法穩(wěn)定所需要滿足的條件為：

(6)

式中，Smax為參考信號(hào)功率譜的最大值。

對(duì)于中等長(zhǎng)度以上的LMS濾波器，式(6)可以保證算法穩(wěn)定，而對(duì)于短濾波器該式也有一定的參考意義[9]。在直達(dá)波和雜波的對(duì)消中，濾波器長(zhǎng)度一般較大(例如，通常需要對(duì)消的雜波范圍可達(dá)數(shù)km，對(duì)于30 MHz的采樣率，濾波器長(zhǎng)度一般需要幾百階)，可根據(jù)式(6)選取步長(zhǎng)參數(shù)的取值上界。

1.3 算法收斂特性分析

在小步長(zhǎng)條件下，LMS濾波器第n時(shí)刻的均方誤差可以寫為[7]：

(7)

式中，

為最優(yōu)濾波器的均方誤差，

Sr(n)=[Sr(n)，Sr(n-1)，...，Sr(n-M)]T，

p=E[Sr(n)x*(n)]，

上角標(biāo)H和T分別代表共軛轉(zhuǎn)置和轉(zhuǎn)置。

可以得到：

(8)

當(dāng)n→∞時(shí)，均方誤差逐漸衰減到如下常數(shù)：

(9)

2 基于聯(lián)合過(guò)程估計(jì)的干擾抑制方法

由上述分析可知，輸入?yún)⒖夹盘?hào)的相關(guān)性對(duì)LMS算法收斂速度影響很大，在雷達(dá)信號(hào)處理中，為了減小采樣引起的目標(biāo)能量損失，一般采樣率會(huì)大于信號(hào)帶寬，此時(shí)LMS濾波器的輸入信號(hào)在相鄰采樣點(diǎn)之間可能存在很大的相關(guān)性。采用聯(lián)合過(guò)程估計(jì)方法，基于格型預(yù)測(cè)對(duì)輸入?yún)⒖夹盘?hào)進(jìn)行去相關(guān)處理，然后通過(guò)基于LMS類的多重回歸濾波算法對(duì)直達(dá)波和雜波估計(jì)，提高算法收斂速度。

2.1 格型預(yù)測(cè)

格型預(yù)測(cè)是一種常用的去相關(guān)方法，它可以將參考信號(hào)轉(zhuǎn)化為彼此之間相互正交的后向預(yù)測(cè)誤差，并且信息量沒(méi)有損失。去相關(guān)之后可以利用多重回歸濾波器將后向預(yù)測(cè)誤差進(jìn)行線性組合，從而實(shí)現(xiàn)對(duì)直達(dá)波和雜波信號(hào)的擬合相消。

格型預(yù)測(cè)器結(jié)構(gòu)如圖1所示，其中，fi(n)和bi(n)(i=0，1，...，M-1)，分別代表參考信號(hào)Sr(n)的前、后向預(yù)測(cè)誤差，κi為反射系數(shù)。零階預(yù)測(cè)誤差f0(n)=b0(n)=Sr(n)，并且前、后向預(yù)測(cè)誤差之間的遞推關(guān)系如下：

(10)

bi(n)=κifi-1(n)+bi-1(n-1)，

(11)

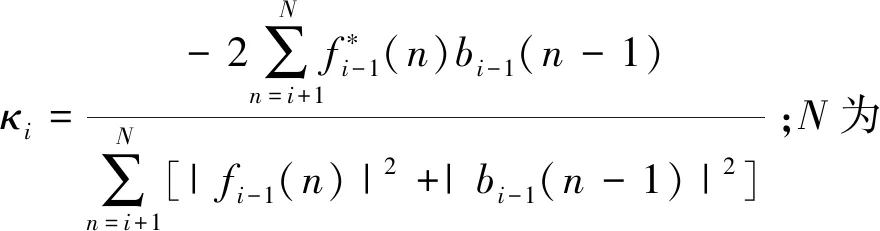
格型預(yù)測(cè)器輸出的后向預(yù)測(cè)誤差bi(n)之間相互正交，即：

(12)

式中，Pi為i階預(yù)測(cè)誤差功率。

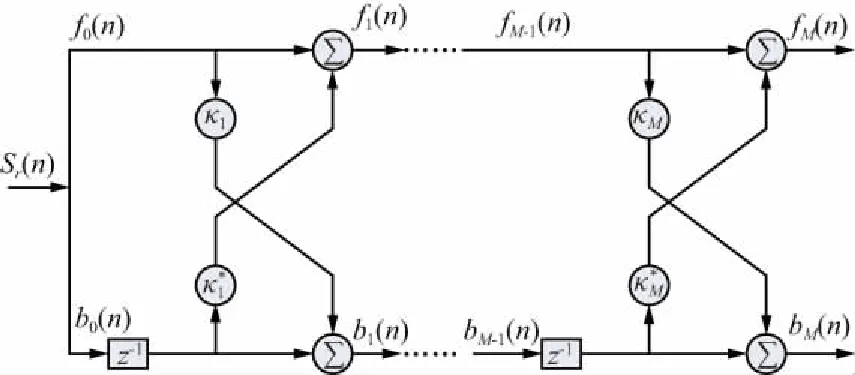
圖1 格型預(yù)測(cè)器結(jié)構(gòu)Fig.1 Structure of lattice filter

對(duì)于非平穩(wěn)輸入信號(hào)，利用梯度自適應(yīng)格型(GAL)算法對(duì)反射系數(shù)進(jìn)行更新，通過(guò)最小化前、后向預(yù)測(cè)誤差功率之和，得到反射系數(shù)的遞歸形式[11]：

(13)

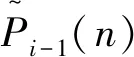
|bi-1(n-1)|2]，

(14)

式中，β為接近于1但是小于1的正數(shù)。

2.2 多重回歸濾波算法

對(duì)參考信號(hào)進(jìn)行去相關(guān)之后，通過(guò)多重回歸濾波器對(duì)直達(dá)波和雜波信號(hào)進(jìn)行估計(jì)。多重回歸濾波器的系數(shù)更新可以采用LMS類型的算法。因?yàn)榇藭r(shí)各抽頭輸入之間變得不相關(guān)，所以LMS類型算法的收斂速度會(huì)得到明顯提高。

NLMS算法采用||b(n)||2作為歸一化參量對(duì)回歸系數(shù)hi(n)進(jìn)行如下調(diào)整：

式中，b(n)=[b0(n)，b1(n)，...，bM(n)]；μ為步長(zhǎng)參數(shù)；·代表向量的模。

如果在hi(n)的調(diào)整中利用λi+1將步長(zhǎng)進(jìn)行歸一化，那么不同的收斂模式將具有相同的收斂速度。考慮到λi+1=Pi，對(duì)于固定系數(shù)的格型預(yù)測(cè)器，采用SNLMS算法對(duì)回歸系數(shù)進(jìn)行調(diào)整：

3 仿真驗(yàn)證

3.1 LMS干擾抑制算法的收斂分析

假設(shè)參考信號(hào)為單位方差的白噪聲，需要對(duì)消的雜波范圍為0～2 km(雙基地距離)，直達(dá)波和雜波的總強(qiáng)度為58 dB，Stnc(n)的大小為0 dB。信號(hào)的采樣率為30 MHz，LMS濾波器的長(zhǎng)度為200階。

圖2給出了此時(shí)對(duì)消剩余的收斂曲線，其中仿真曲線為10次蒙特卡洛仿真平均得到的結(jié)果。可以看出，仿真曲線與理論結(jié)果一致，并且步長(zhǎng)參數(shù)越大，算法收斂越快，但是對(duì)于不同的步長(zhǎng)，收斂后對(duì)消剩余的區(qū)別并不明顯，這是因?yàn)槭諗亢蟮某烤秸`差相對(duì)Jmin小很多。一般情況下，如果超量均方誤差可以達(dá)到與Jmin相同的水平或者比Jmin更小，可以認(rèn)為得到了較為滿意的對(duì)消結(jié)果。

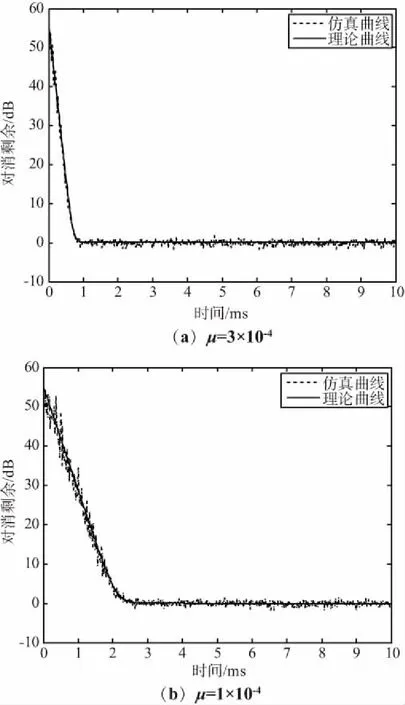
圖2 非相關(guān)輸入情況下的對(duì)消剩余收斂曲線Fig.2 Convergence curve of cancellation residue for uncorrelated input

如果參考信號(hào)為低通濾波后的噪聲調(diào)頻信號(hào)，其帶寬為10 MHz，圖3給出了此時(shí)對(duì)消剩余e(n)的收斂曲線。可以看出，在相同步長(zhǎng)條件下算法的收斂速度變慢。這是由于此時(shí)參考信號(hào)的相鄰采樣點(diǎn)之間具有相關(guān)性，相關(guān)矩陣Rr的特征值擴(kuò)展明顯變大(其最大特征值約為3.13，最小特征值約為7.5×10-10)。較小特征值對(duì)應(yīng)的自然模式收斂較慢，從而導(dǎo)致算法的整體收斂速度變慢。

在圖3(a)中，5 ms之后算法基本達(dá)到收斂。這樣的收斂速度對(duì)于靜態(tài)雜波來(lái)說(shuō)已經(jīng)足夠，但是如果雜波的多普勒頻率較大，5 ms的收斂時(shí)間可能是不滿足要求的。例如，在強(qiáng)風(fēng)狀態(tài)下，植被的速度譜展寬可達(dá)0.5 m/s[12]，對(duì)于10 GHz的工作頻率，相應(yīng)的雜波多普勒頻率為33 Hz，此時(shí)上述收斂速度就顯得過(guò)慢。

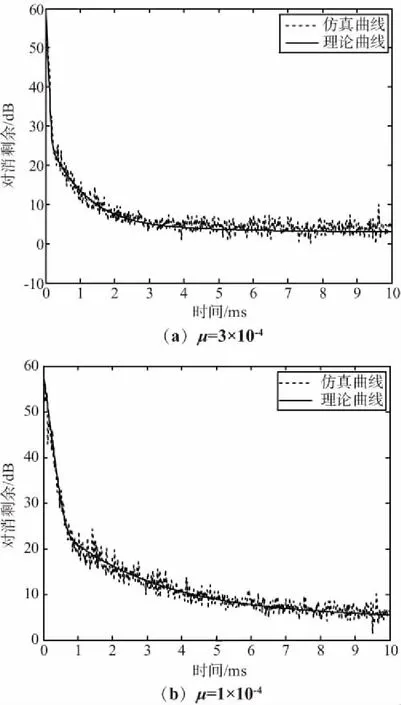
圖3 相關(guān)輸入情況下的對(duì)消剩余收斂曲線Fig.3 Convergence curve of cancellation residue for correlated input

3.2 聯(lián)合過(guò)程估計(jì)算法的收斂分析

3.2.1 固定反射系數(shù)條件下的收斂分析

假設(shè)最遠(yuǎn)雜波的(雙基地)距離為2 km，直達(dá)波和雜波的總強(qiáng)度為46 dB。在樣本數(shù)為1 000的情況下，計(jì)算得到相應(yīng)的反射系數(shù)。

在聯(lián)合過(guò)程估計(jì)中，格型預(yù)測(cè)器采用該反射系數(shù)對(duì)輸入?yún)⒖夹盘?hào)進(jìn)行去相關(guān)，得到的對(duì)消輸出結(jié)果如圖4所示，其中FL-SNLMS和FL-NLMS分別代表基于固定系數(shù)格型預(yù)測(cè)器的SNLMS算法以及NLMS算法。需要注意的是，由于自適應(yīng)過(guò)程中輸出信號(hào)起伏較大，為了便于觀察，對(duì)對(duì)消結(jié)果進(jìn)行了100點(diǎn)(3.3 μs)的平滑處理。

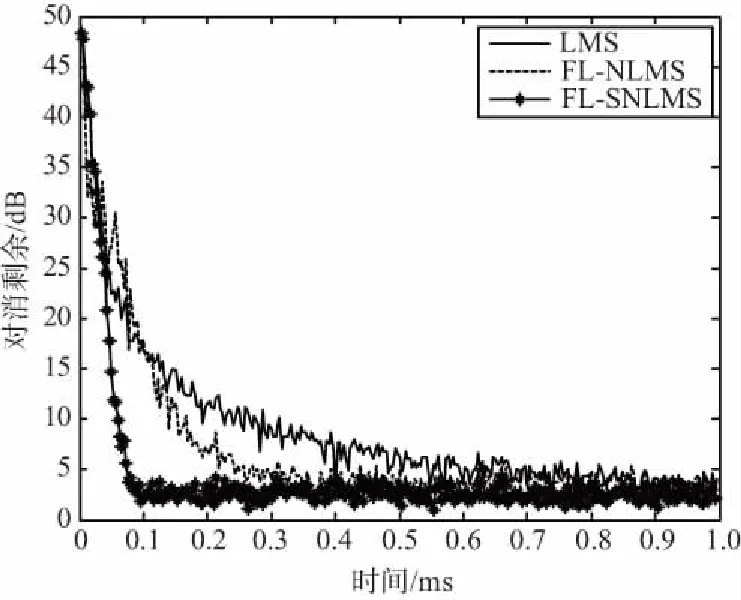
圖4 固定反射系數(shù)條件下聯(lián)合過(guò)程估計(jì)算法的收斂曲線Fig.4 Convergence curve of joint process estimator for fixed reflection coefficient

雖然LMS算法在初始階段收斂較快，但是隨著迭代次數(shù)增加，其收斂速度逐漸下降，與其他算法相比，在0.3 ms之后其對(duì)消剩余最大。FL-NLMS算法在初始階段收斂速度較慢，但是在0.4 ms之后基本達(dá)到收斂，最終的對(duì)消剩余在3 dB左右。FL-SNLMS算法具有最快的收斂速度，僅需0.1 ms就可以達(dá)到收斂，收斂后的輸出誤差與FL-NLMS算法基本相同。另外，可以看出，F(xiàn)L-SNLMS算法的收斂速度近似是恒定的，與理論分析一致。

3.2.2 GAL算法下的收斂分析

當(dāng)反射系數(shù)采用GAL算法進(jìn)行自適應(yīng)更新時(shí)，圖5(a)給出了相應(yīng)的NLMS和SNLMS算法收斂曲線。在GAL算法中，參數(shù)β=0.99，z=0.001；NLMS和SNLMS算法的參數(shù)設(shè)置與上述仿真相同。

在圖5(a)中，GAL-NLMS算法和GAL-SNLMS算法的初始收斂速度較快，但是與LMS算法相比，它們的對(duì)消剩余都很大。這是由于GAL算法每對(duì)反射系數(shù)進(jìn)行一次更新，NLMS算法和SNLMS算法就需要重新對(duì)回歸系數(shù)進(jìn)行調(diào)整。所以在聯(lián)合過(guò)程估計(jì)中，GAL算法必須在一段時(shí)間之后停止對(duì)反射系數(shù)進(jìn)行更新。

如果反射系數(shù)在0.17 ms之后停止更新，GAL-NLMS和GAL-SNLMS算法的輸出誤差會(huì)快速收斂到較低的水平，如圖5(b)所示。此時(shí)這2種算法會(huì)比LMS算法更快達(dá)到收斂狀態(tài)。

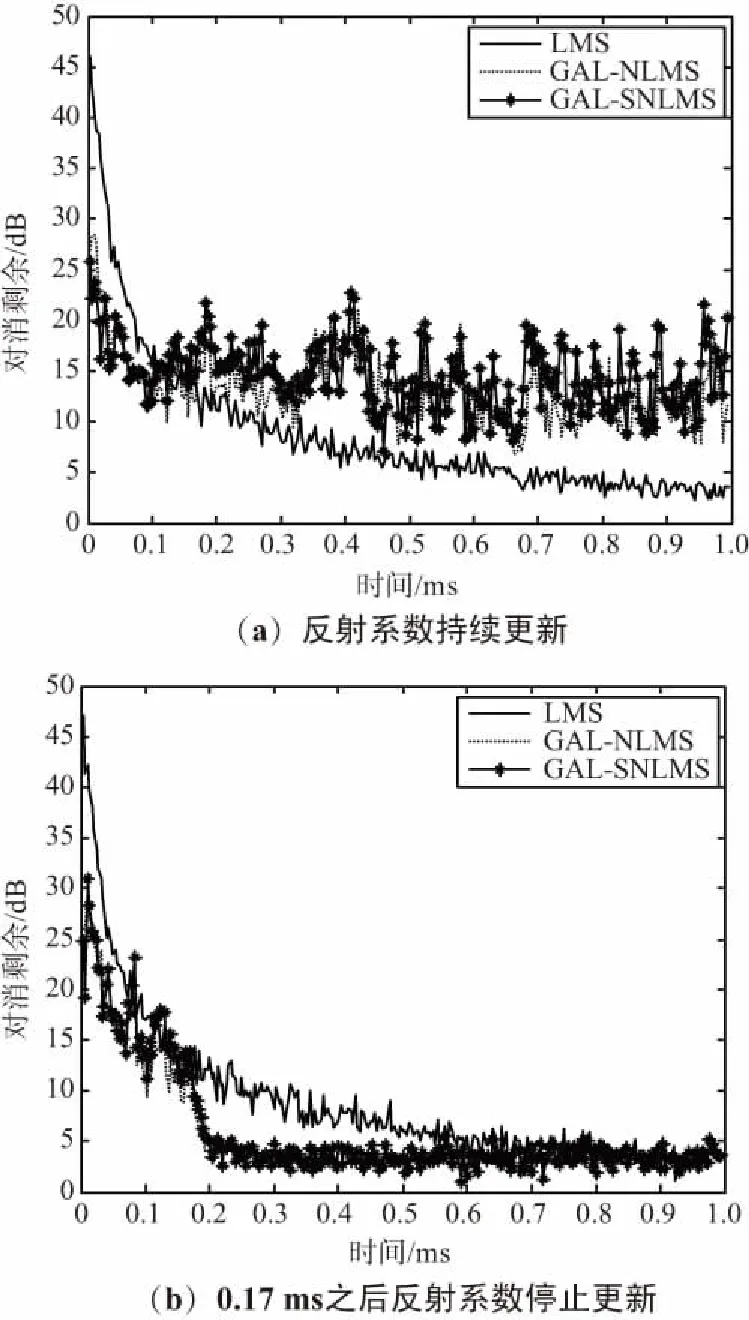
圖5 GAL算法下的收斂曲線Fig.5 Convergence curve of gal algorithm

4 結(jié)束語(yǔ)

在雙基地噪聲雷達(dá)中直達(dá)波和近距雜波抑制過(guò)程中，由于參考信號(hào)自相關(guān)矩陣的特征值擴(kuò)散較大，傳統(tǒng)LMS類對(duì)消算法收斂速度很慢，難以滿足低速雜波抑制的需求；本文采用格型預(yù)測(cè)器對(duì)參考信號(hào)進(jìn)行去相關(guān)處理，提高算法的收斂速度。但是，對(duì)于平穩(wěn)的參考信號(hào)最好采用固定的反射系數(shù)，采用基于GAL的抑制算法會(huì)引起對(duì)消剩余的增大。