基于遺傳算法的行李碼放機械臂軌跡優化

何銘鑫 張倩倩 陳治華 步亞

摘? 要：根據行李碼放機械臂運動學與動力學約束，提出一種基于遺傳算法的機械臂軌跡優化方法。優化方案以關節速度和加速度為約束條件，優化目標為時間最優或者關節加加速度最優，為提高算法收斂效率，用改進的遺傳算法得到初始的種群，采用4-5多項式曲線對關節軌跡進行擬合，該方法對提高機械手臂的關節軌跡的平滑性有明顯效果，最終實現關節加加速度和機械臂時間的最優的軌跡規劃;模擬結果表明，該方法可以有效提高貨碼放穩定性與效率。

關鍵詞：航空行李碼放? 機械臂軌跡規劃? 4-5多項式曲線? 遺傳算法

中圖分類號：TP242? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ?文章編號：1674-098X（2020）10（a）-0001-06

Abstract： According to the kinematics and dynamic constraints of the baggage stacking robot， a trajectory optimization method based on genetic algorithm is proposed. The optimization scheme takes joint speed and acceleration as constraints， and the optimization goal is time optimization or joint acceleration. In order to improve the convergence efficiency of the algorithm， the improved genetic algorithm is used to obtain the initial population， and the 4-5 polynomial curve is used to perform the joint trajectory. The fitting method can effectively improve the smoothness of the joint trajectory of the robot arm， and finally achieve the optimal trajectory planning of the joint acceleration and the robot arm time; the simulation results show that this method can effectively improve the stability and efficiency of the cargo storage.

Key Words： Aviation baggage stacking;Robot arm trajectory planning;4-5 polynomial curve;Genetic algorithm

近年來，隨著國內民航業的快速發展和智慧機場的加快建設，實現航空貨物和行李的自動裝卸與碼放勢在必行。如何實現貨物與行李的自動化裝載，改善行李碼放效率與碼放質量，是機場迫切需要解決的關鍵問題。行李碼放環節勞動強度大，招工難問題日益顯現。發展自動裝卸行李、托運行李的相關技術是機場企業的必然選擇。

目前，針對機械臂的軌跡規劃問題國內外的學者均對其進行了大量的研究。李進文等人提出了一種等時間周期的直線插補算法針對PLC控制器的機器人，并且得到成功應用[1]。權龍哲成功的把圓弧插補算法用在機器人中[2]，但是圓弧插補算法的精度高會影響規劃的速度，所以在精度與速度之間需要更多的斟酌。葉仁平等人[3]提出了一種NURBS曲線自適應實時前瞻插補算法，可以將機器人的端部位移實時轉換為軌跡插補點，實際表明該方法可以實現對機器人曲線軌跡規劃的要求。傅霞君等人[4]提出了一種對機器人機械臂各關節的動力學參數進行離線識別的新方法，該方法不僅能識別機械臂的動力學參數，還能識別動摩擦系數和黏滯摩擦系數。

綜上所述，從以上研究學者的成果可以看出，對于軌跡規劃的插值算法的研究學者有很多，但滿足實時要求的插值算法相對較少。此外，優化算法都具有各自的優缺點，因此很難找到一種將兩者都考慮在內的算法來獲得最佳軌跡。本文采用遺傳算法對機械臂的軌跡進行規劃，在提高機械臂的運行效率的同時，不僅保證了機械臂的運行穩定性，還滿足了機械臂的收放的需求。

1? 機械臂軌跡規劃

1.1 機械臂運動學建模

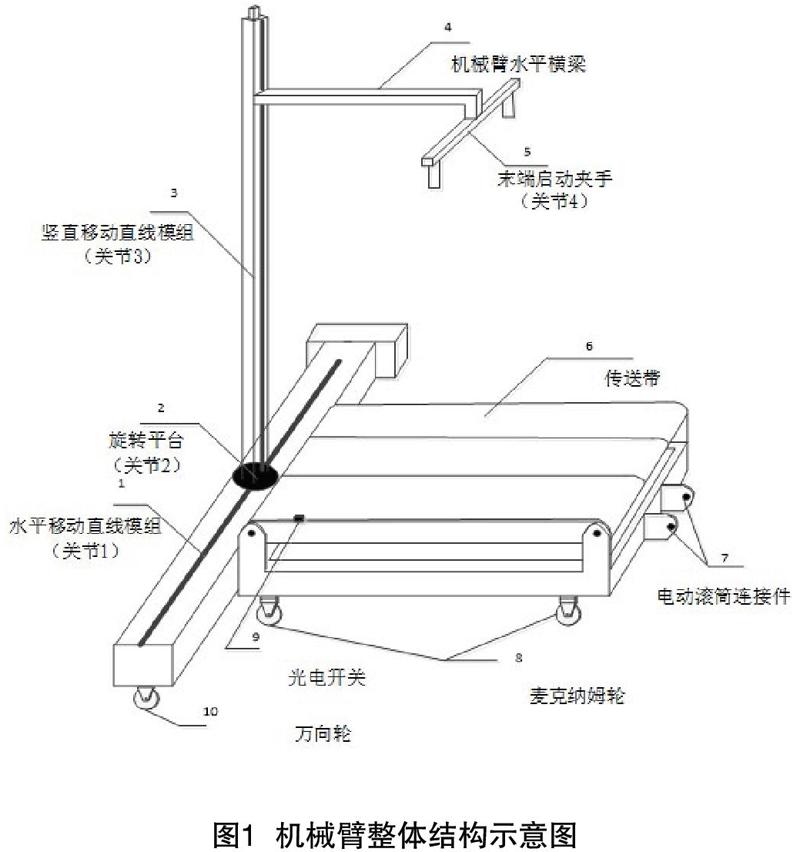
本文采用的航空行李收放機械臂的整體結構示意圖如圖1所示，其機械結構主要包括圓柱式機械臂、行李位置、姿勢調節平臺和運動平臺等。電源模塊和電路控制模塊等附屬單元模塊在移動平臺的內部空閑位置。

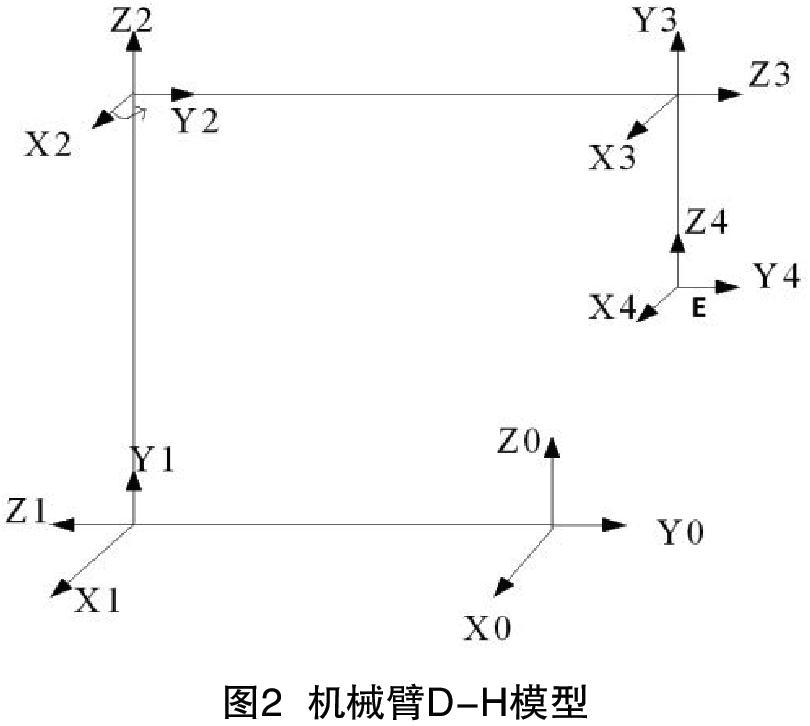
本文研究的機械臂為可移動機械臂，結構示意圖如圖1所示。機械臂各個關節連桿在空間內的姿態和位置是通過改進型的D-H模型來描述，在每個桿件的起始點設立對應的直角坐標系按照連桿結構建立機械臂D-H數學模型如圖2所示。設定機械臂移動平臺最前方中間位置作為整個機械臂的坐標原點O，將相鄰的關節連桿分別設置為1號、2號、3號、4號關節連桿。

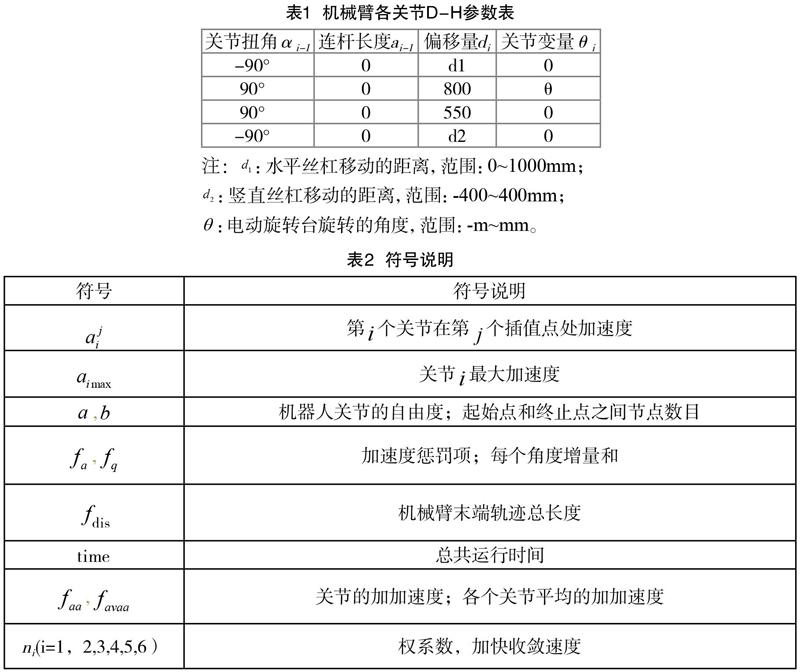
得到機械臂的D-H參數如表1所示，其依據圖1與圖2以及機械臂的尺寸參數所得。為機械臂的運動學分析、軌跡規劃奠定了理論基礎。

航空行李碼放機械臂由一個旋轉關節，兩個平移關節以及一個末端夾持器組成，通過3個步進電機和末端執行器的氣動氣缸驅動。由于末端的夾持器只是涉及松夾功能，因此它對機械臂的整體運動學仿真沒有影響。

1.2 軌跡優化目標的選擇

軌跡規劃是為了使機械臂完成工作任務，以便使末端抓取器位于給定的起點和所需的終點之間，根據優化目標找到最佳的軌跡，并確定機械臂每個關節的位移、速度和加速度曲線變化。根據關節插值的原理[5]，使用4-5插值多項式進行軌跡規劃，使整個軌跡曲線的位置、速度和加速度保持連續。這種軌跡形成的優點是容易處理機械臂的動態約束并且計算速度快。

為提高機械臂的工作效率，同時保證機械臂不受到損壞，同時考慮到目前國內航班允許的免費行李質量大部分在10～20kg之間，本文針對質量在10～20kg不同重量的行李采用機械臂運行時間和關節平均加加速度（脈動）的優化目標進行軌跡優化，使得機械臂的運行更加合理[6]。以運行時間和關節加加速度（脈動）為優化目標，當行李重量大于10kg小于20kg時，在保證機械臂工作效率的同時，考慮了運動過程中對機械臂的關節的影響，防止機械臂的關節因過度撞擊而損壞。

1.3 優化目標和約束條件

本文將不同重量的行李箱使用不同的優化目標來進行機械臂的軌跡規劃，可以保障機械臂的工作效率，同時保障機械臂不受損害并且對機械臂的關節影響最小。在滿足所有約束的前提下，優化目標為讓整個關節的移動時間最短或在工作過程中對機械臂的影響最小，機械臂軌跡規劃的優化目標的表達形式如下所示：

上述公式中，是每段多項式的第個關節隨時間變化的速度，是第個關節的最大運行的速度，，分別是第個關節的多項式段的加速度;是第個關節最大的加速度。

總的工作時間，選擇時間或加加速度為優化目標，采用遺傳算法，使得或者平均加加速度在允許的范圍之內，則軌跡規劃目標優化參數為。

1.4 基于遺傳算法的優化求解

遺傳算法是基于自然界中的生物進化模型開發的隨機全局搜索和優化方案[7]。通過利用遺傳算法實現機械臂的軌跡規劃優化的過程如下。

（1）參數編碼。

針對本文的優化問題，設計8個優化參數，可以實現實數編碼，使效率提高。

（2）種群初始化。

采用近似算法改進的遺傳算法來獲得更好的初始種群，實現算法的全局最優同時加快算法的運算速度。

（3）參數計算。

多項式的未知參數通過多組優化的目標來求解，推導多項式后判斷多項式是否滿足速度的約束條件。

（4）適應度函數設計。

設計適應度函數應滿足機械臂的運動以滿足收斂到運動學約束的條件[8]。懲罰函數用作進行約束極值優化的目標函數，公式（5）和（6）是約束加速度的懲罰項。為了加快收斂速度，目標函數添加了關節行進總距離和空間軌跡長度的約束，公式（7）為適合度函數。

針對上式的符號說明如表2所示。

為了避免陷入局部最優，前期，，的權系數比大，后期，，的權系數比小，，值比的大。

（5）遺傳操作步驟。

在個體之間選擇具有最佳適合度的一代，將該代種群進入下一代。該比賽選擇方法避免了在解決最小化問題時輪盤賭選擇策略需要轉換適合度值的問題。

交叉重組方法對兩個親本染色體進行交叉操作，同時按公式（10）產生子個體，且子個體在每一代種群中出現交叉的概率為。

子個體=父個體1+α（父個體2-父個體1）（10）

是區間為的均勻隨機數組。

變異 算法后期會出現停滯的現象，這導致收斂速度將大大降低。因此要引入變異算子，增強算法的局部搜索能力，從而可以避免算法陷入局部最優的情況。

（6）選擇終止進化代數為100作為代數遺傳終止的條件，如圖3所示是遺傳算法的具體實現步驟。

2? 仿真結果分析

不同重量的行李分別采用不同的優化目標，得到更合理的機械臂運行的狀態，仿真結果如圖4所示。

當行李重量10≤m≤20kg，優化目標為運行時間和關節加加速度。優化目標的約束范圍為：，，，，，，，結果如圖4所示。

從以上仿真結果可以看出，機械臂的開始運行時間在20s左右的時刻，插值時間為，，最大加加速度的值在允許的范圍之內，值為，雖然運行時間有所增加，但卻使機械臂的運行安全得到保障。

3? 結語

本文以航空行李碼放機械臂的軌跡優化為研究對象，通過結合遺傳算法及機械臂的動力學與運動學的約束，提出了一種機械臂軌跡優化的方法，在算法初期，為減少算法收斂時間，加入了改進的遺傳算法，通過該算法得到了一個較好的初始種群。機械臂的軌跡優化方法將關節速度及其加速度作為約束條件，時間最優或者關節加加速度最優作為目標，為提高機械臂關節軌跡的平滑性，采用了4-5多項式曲線對關節軌跡進行擬合的方法，通過上述方法實現機械臂時間和關節加加速度最優的軌跡規劃，最后仿真結果表明該方法的有效性。

參考文獻

[1] 李進文， 何素梅， 吳海彬.一種直線插補算法及其在機器人中的應用研究[J].機電工程，2015，32（7）： 966-970.

[2] 權龍哲，彭濤，沈柳楊，等.立體苗盤管理機器人的機械臂參數優化與試驗[J].農業工程學報， 2017（7）：17-26.

[3] 葉仁平，曾德懷.基于NURBS曲線自適應實時前瞻插補算法研究[J].機床與液壓，2016，44（13）：46-52.

[4] 傅霞君，袁建軍，王帥，等.基于粒子群算法的機器人動力學參數辨識[J].機電一體化，2017，23（2）：3-8，64.

[5] 鄭天江，李俊杰，陳慶盈，等.基于三次B樣條的移動機器人實時軌跡規劃研究[J]. 制造業自動化，2017， 39（5）：4-7.

[6] 權龍哲，彭濤，沈柳楊，等.立體苗盤管理機器人的機械臂參數優化與試驗[J].農業工程學報，2017， 33（7）：10-19.

[7] 任亞冰.基于機器學習的機械臂運動規劃研究[D].成都：電子科技大學，2019.

[8] 步亞.航空行李碼放機械臂軌跡規劃與控制方法研究[D].天津：中國民航大學，2019.