線路工程帶狀走廊三維地形構建及輕量化研究

宋偉華，譚衢霖，夏 宇，祝 清

（1.北京交通大學 土木建筑工程學院，北京 100044；2.北京交通大學 線路工程勘測空間信息研究所，北京 100044）

三維地形建模和可視化是在計算機上對地形數據進行三維顯示、模擬仿真、簡化、多分辨率表達和網絡傳輸的一項技術，它涉及到測繪學、現代數學、計算機三維圖形學、計算幾何、地理信息系統、虛擬現實、科學計算可視化、計算機網絡等眾多學科領域[1]。利用計算機三維可視化技術，將遙感影像和數字高程模型（DEM，Digital Elevation Model）相疊加，可以建立逼真的三維地形環境[2]。

在三維地形建模和可視化研究方面，文獻[3]研究了基于三角形網格的地形建模的基本理論和方法,包括規則數據的三角網生成以及不規則三角網（TIN，Triangulated Irregular Network）的生成算法；文獻[4]應用遙感影像與DEM數據，基于Infraworks平臺建立了某線路段地形、構造物、沿線附屬設施等三維可視化模型；文獻[5]通過層次細節技術和基于網格的模型簡化技術對三維地形建模進行簡化，并且對該技術進行了相應的改善，從而能夠更好地實現三維地形建模簡化技術的應用。

為了滿足實時三維繪制與漫游的需求，減少數據量，且保證數據的必要精度，本文主要針對三維地形空間數據的海量特性，試驗了三維地形構建的2種常用表達模型，并對其輕量化處理方法進行了研究。

1 DEM數據

1.1 DEM數據概述

DEM是用于構建線路工程三維地形的重要信息之一，它描述了地面高程信息，是對地形表面形態的離散化數字表達[6]。線路是一個狹長帶狀構造物，三維地形建模僅需線路中線兩側一定寬度內的DEM數據，可根據直線、曲線、多邊形等不同的提取方法來提取所需范圍內的地形模型數據。

1.2 DEM數據獲取

DEM的獲取方法主要有地面測量、航空攝影測量、衛星立體測圖、衛星定位測量、采集現有地形圖、干涉雷達等[7]。DEM獲取方式如表1所示。通常可直接獲取的DEM數據源如表2所示。

表1 DEM獲取方式列表

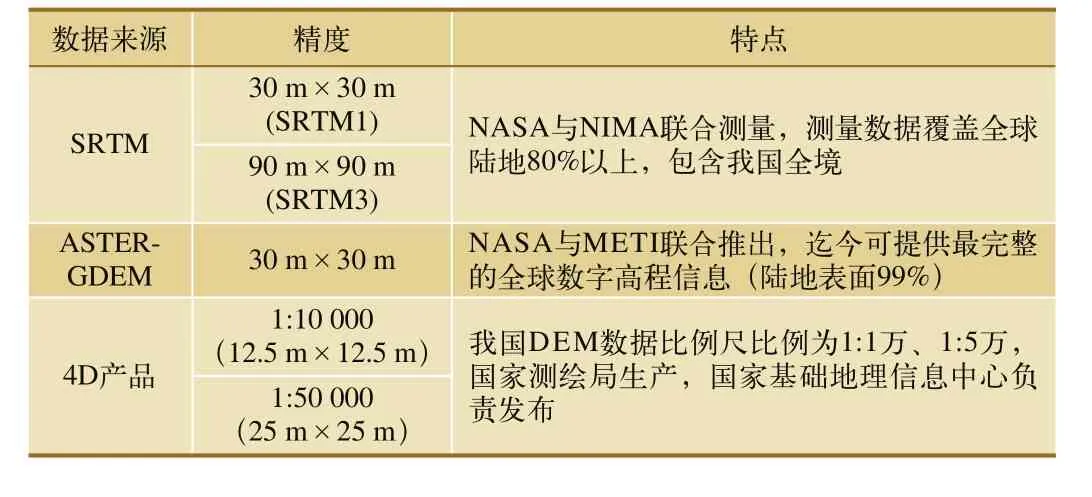
表2 DEM數據來源列表

2 地形模型構建及輕量化

2.1 地形模型表達

目前，用于線路設計的數字地形模型主要有方格網式、三角網式、離散式、分塊離散型和魚骨式模型[8]。其中應用最為廣泛的是方格網式和三角網式。

方格網數字地形模型通常被分割為規則的正方形、矩形或三角形等網格，規則網格將區域空間切分為規則的格網單元，每個格網單元存儲了相應的高程值，如圖1 a所示。方格網數字地面模型（DTM，Digital Terrain Model）適合數據的存儲、分割、合并、內插，便于計算區域內等高線、坡度、坡向、山坡陰影等地理要素，適用于分布較為規則的地形環境，在線路設計領域已成功運用于狹長窄帶線路優化設計之中。但是，方格網DTM數據的分辨率單一，不能精確表示地形的結構細部，難以表達復雜地形的突變現象，在地形平坦的區域存在大量的數據冗余，造成數據量過于龐大，給數據信息管理帶來諸多困難。

TIN原始數據點間無任何聯系且隨機分布，將地形點覆蓋在數字模型區域上的三角形的各頂點，利用分布不規則的數據生成連續的三角面來逼近地形表面，高程由該點所處的三角形區域確定，如圖1 b所示。TIN沒有改變原始數據點，其精度高，便于表征特征性、斷裂線、邊界線，既適用于規則分布的數據，也適用于不規則分布的數據。

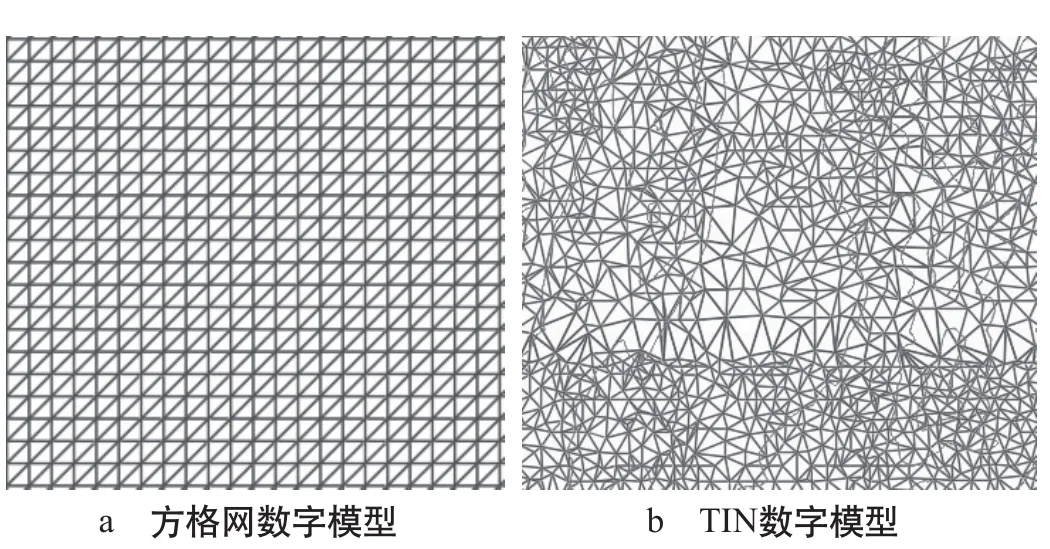
圖1 數字地形模型

本文分別利用DTM和TIN數字模型建立三維地形曲面，地形曲面數據對比如表3所示。對比發現，主要曲面參數（如最小高程、最大高程）沒有區別，但在最大坡率上出現了較大的變動。TIN模型能用更少的數據來精確地表示含有大量斷裂線和構造線的地形表面，更精確合理地表達復雜地表形態，從而使建立的三維地形環境更為精確。故本文選用TIN進行三維地形環境建模。

2.2 Delaunay三角剖分

2.2.1 Delaunay三角剖分性質

如何把離散集合剖分成不均勻的三角形網格，即散點集的三角形剖分問題，是建立三維地形環境的關鍵[9-10]。實際中運用最多的三角剖分方法是Delaunay三角剖分法。Delaunay三角剖分法有2個重要性質。

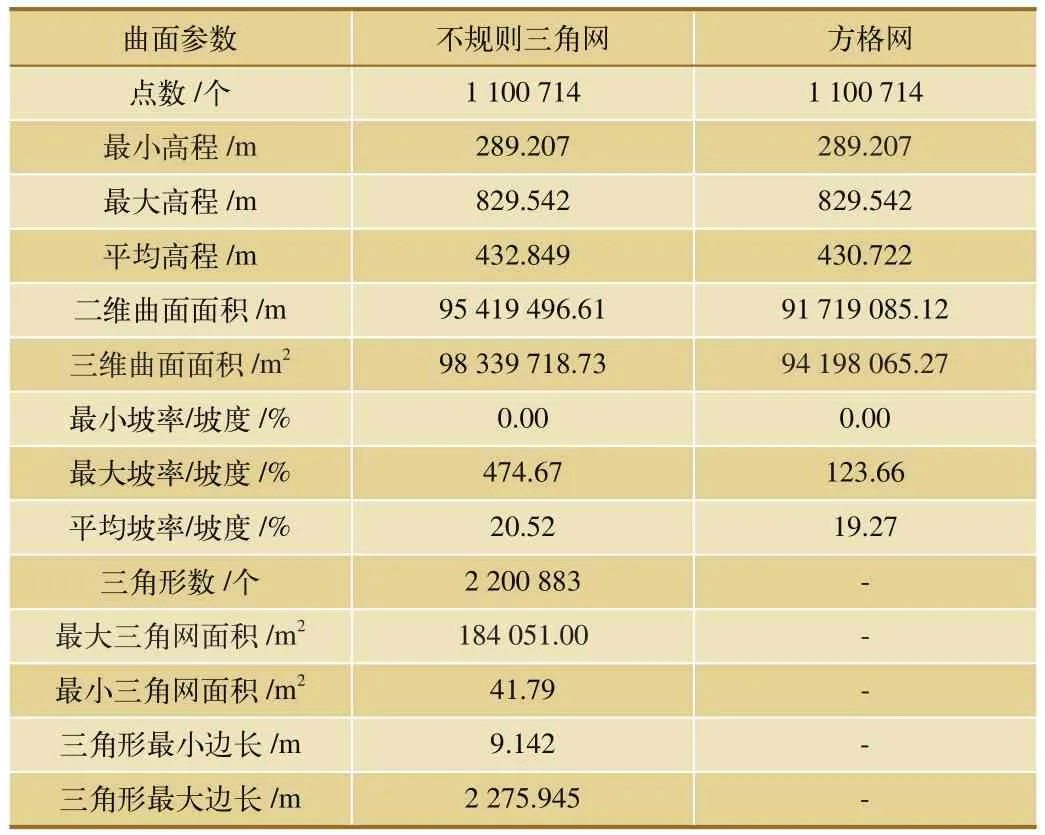
表3 不同數字地形曲面參數對比列表

（1）空外接圓性質

Delaunay三角網是一系列相連但不重疊的三角形的集合，在Delaunay三角網中任一三角形的外接圓范圍內不會有其他點存在。如圖2所示，設AB邊是三角形ABC和三角形ABD的公共邊。若D點不落在三角形ABC的外接圓內，則稱AB邊是局部最優化的，即該三角形具有空外接圓特性。當三角形不具備外接圓特性時，則交換對角線生成另一種三角劃分，使得三角形具有空外接圓特性，該過程稱為局部優化過程（LOP ，Local Optimization Procedure）。

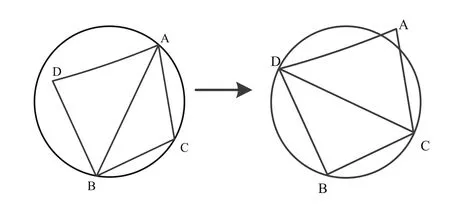
圖2 局部優化過程示意圖

（2）最大化最小角特性

在散點集可能形成的三角剖分中，Delaunay三角剖分所形成的三角網的最小角最大，是最接近于規則化的的三角網。其任意2個相鄰的三角形構成的凸四邊形，在相互交換對角線后，6個內角的最小角不再增大，如圖3所示。

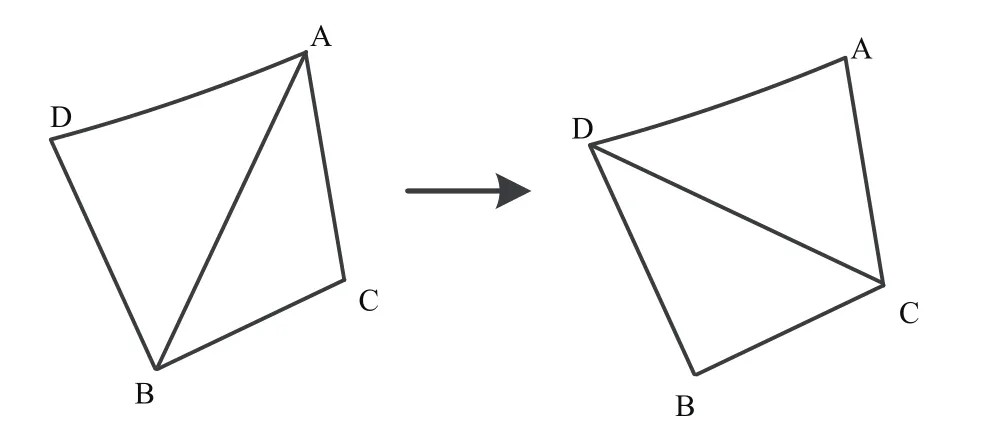
圖3 最大化最小角示意圖

2.2.2 Delaunay三角網生成算法

根據構建TIN算法的實現過程，可將Delaunay三角網生成算法劃分為分治算法、三角網生長法和逐點插入法[11-12]。分治算法將點集劃分到足夠小，使其易于生成三角網，然后把局部三角網合并生成最終的三角網，劃分過程中，用LOP算法保證Delaunay三角網的構建；三角形生長算法先找出點集中相距最短的2點，將其連接成為一條Delaunay邊，然后按判別法搜尋包含此邊的另一端點，并依次處理所有新生成的邊；逐點插入法先在包含數據點的一個多邊形中建立初始三角網，再將剩余的點逐一插入，用LOP算法構建Delaunay三角網。

三角網生長算法時間效率低下，目前較少采用；分治算法復雜度較優，但需要占據較大的內存空間且預處理和優化工作量較大；逐點插入法實現簡單、占用內存小，但時間復雜度差、運行速度慢。由于線路工程里程較長、方案較多，為保證精度導致所取離散點數目較多，需對數字地形模型維護和更新等原因，在綜合分析各算法優劣的基礎上，采用內存占用較小的逐點插入算法，算法流程如下：

（1）建立初始三角網，如圖4所示，給定點集的包容盒 Box（Xmin，Xmax，Ymin，Ymax）并將其剖分為2個初始三角形A，其中，Xmin為數據點X坐標極小值；Xmax為數據點x坐標極大值；Ymin為數據點y坐標極小值；Ymax為數據點y坐標極大值。

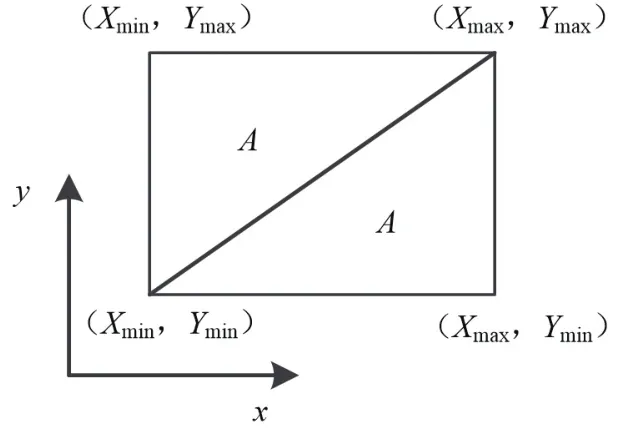
圖4 初始三角形剖分示意圖

（2）從點集中取出一點P，在已建立的三角網中找到包含該點的三角形進行定位，如圖5 a所示。

（3）在包含P點的三角形拓撲關系中，利用空外接圓性質找出外接圓包含的三角形集合，其外邊界即為要確定的影響域，如圖5 b所示。設三角形abc，如圖6所示，按逆時針排列，空外接圓性質判斷按公式（1）計算。若F＜0，則d在外接圓內側；若F＞0，則d在外接圓外側；若F=0，則d在外接圓上。

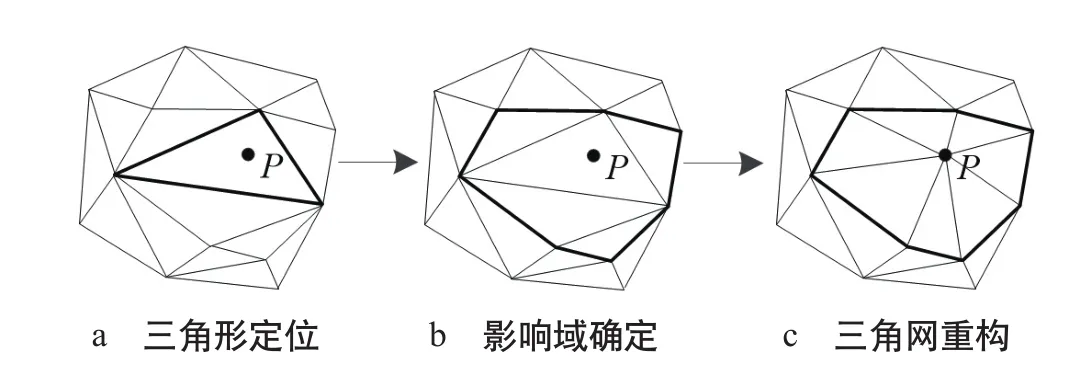
圖5 插入P點重構三角網過程圖

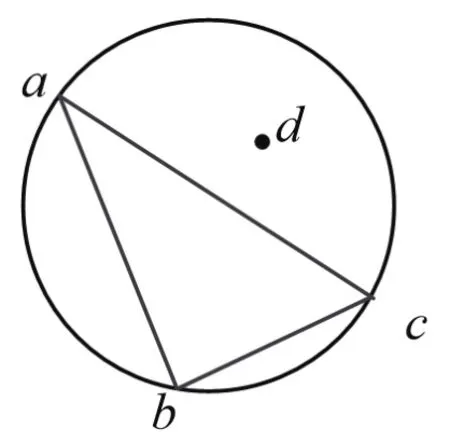
圖6 空外接圓判斷示意圖

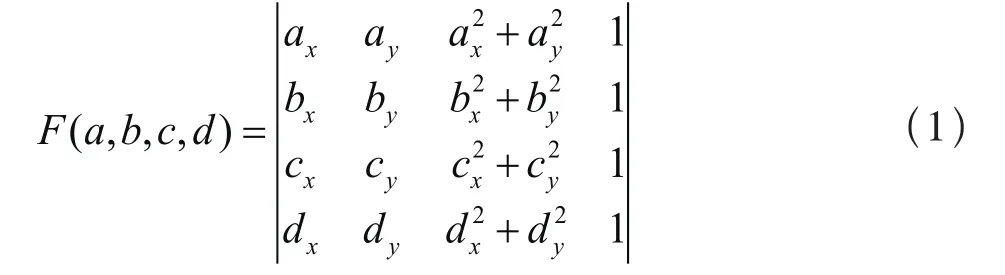
其中，ax、ay、bx、by、cx、cy、dx，dy分別為數據點a、b、c、d的橫縱坐標。

（4）依據Delaunay性質在影響域內進行三角網重構，將影響域各邊界交點與插入點順次連接，即得插入點后重構的三角網，如圖5 c。

（5）待所有點內插完后，刪除邊界冗余三角形。將獲取的DEM數據根據Delaunay三角剖分算法構建TIN，建立三維地形曲面模擬地形空間分布。圖7為試驗區域的TIN模型，圖8為三維地形曲面模型。

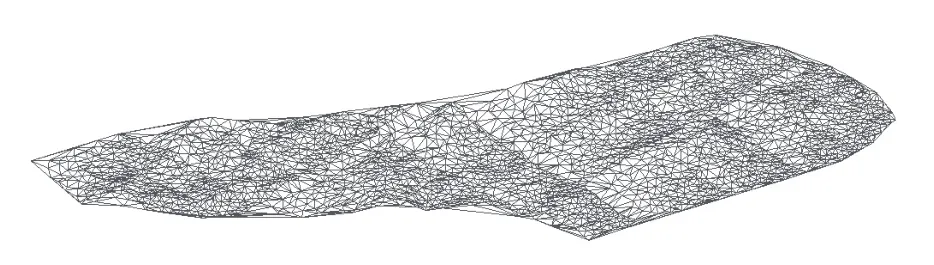
圖7 線路走廊帶TIN模型示意圖

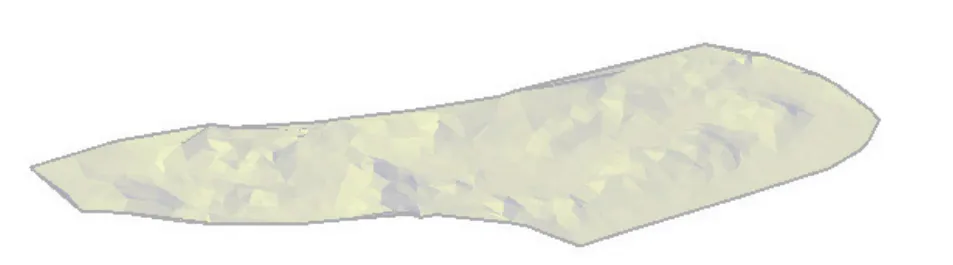
圖8 線路走廊帶三維地形曲面模型示意圖

2.3 數據輕量化

由于線路具有工程距離長、覆蓋范圍廣的特點，導致根據Delaunay三角剖分建立的三維地形曲面數據量較大。臃腫的三維曲面數據造成系統運行緩慢，為后續的線路設計帶來困難。因此，需要對海量的數據進行簡化處理來優化曲面性能，在保證地形曲面精度的同時減少數據量的冗余。數據輕量化主要有邊緣收縮法和點刪除法2種方式。

2.3.1 邊緣收縮法

邊緣收縮法使三角形的一條邊收縮到單一點，每次邊緣收縮可以刪除一個點，同時減少2個三角形。設每個三角形平面方程為：

其中，a，b，c，d為三角形平面方程的系數。

定義p=[a b c d]T，則每個三角形的矩陣誤差為：

頂點v的誤差矩陣為環繞網格頂點周圍三角面片的平均矩陣誤差∑Q/n，n為環繞在網格頂點v周圍的三角面片的個數，即誤差為：

其中，v為三角形收縮邊的頂點坐標。

三角形收縮邊緣的頂點v1和v2合并到新頂點v，其邊緣收縮的誤差為：

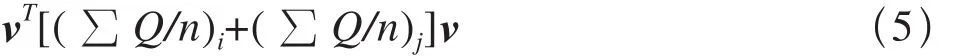
誤差最小點即為新頂點，同時刪除誤差較大的點，方法過程如圖9所示。

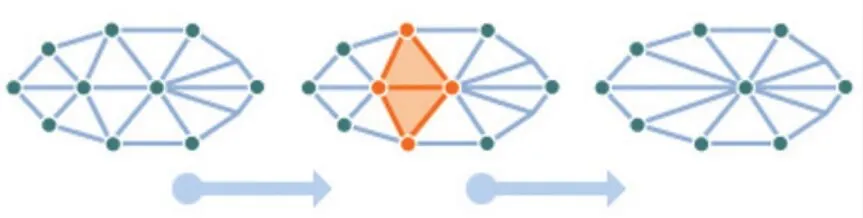
圖9 邊緣收縮簡化示意圖

2.3.2 點刪除法

點刪除法按照簡化比例進行曲面點的選擇和刪除，刪除三角網格中，在高程容許誤差范圍內，且不會導致拓撲結構改變的點。高程容許誤差范圍計算公式為：

其中，h為初始高程；h'為刪除點后的高程；ε為容許誤差。

同時對由此刪除操作引起的空洞進行三角化再構建TIN，方法過程如圖10所示。

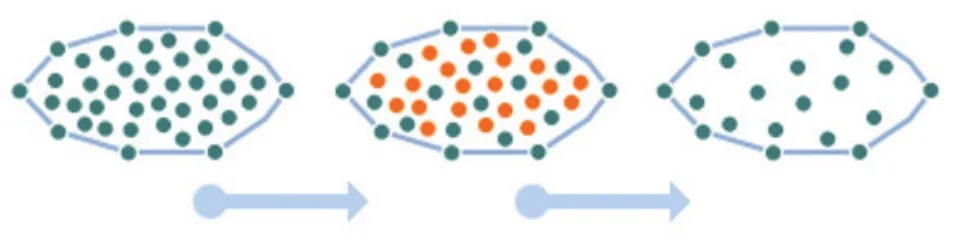
圖10 點刪除簡化示意圖

2.3.3 方法對比

基于原始DEM數據構建地形曲面，分別采用邊緣收縮法和點刪除法對原始地形曲面進行簡化，2種方法刪除點數所占百分比均為50%，詳細參數如表4所示。由表4中參數對比分析可知，利用邊緣收縮法簡化曲面后，曲面的最大坡率、最小三角網面積等參數出現了較大波動，而利用點刪除法對曲面可進行有效地簡化，且曲面參數未發生明顯改變，失真較小。

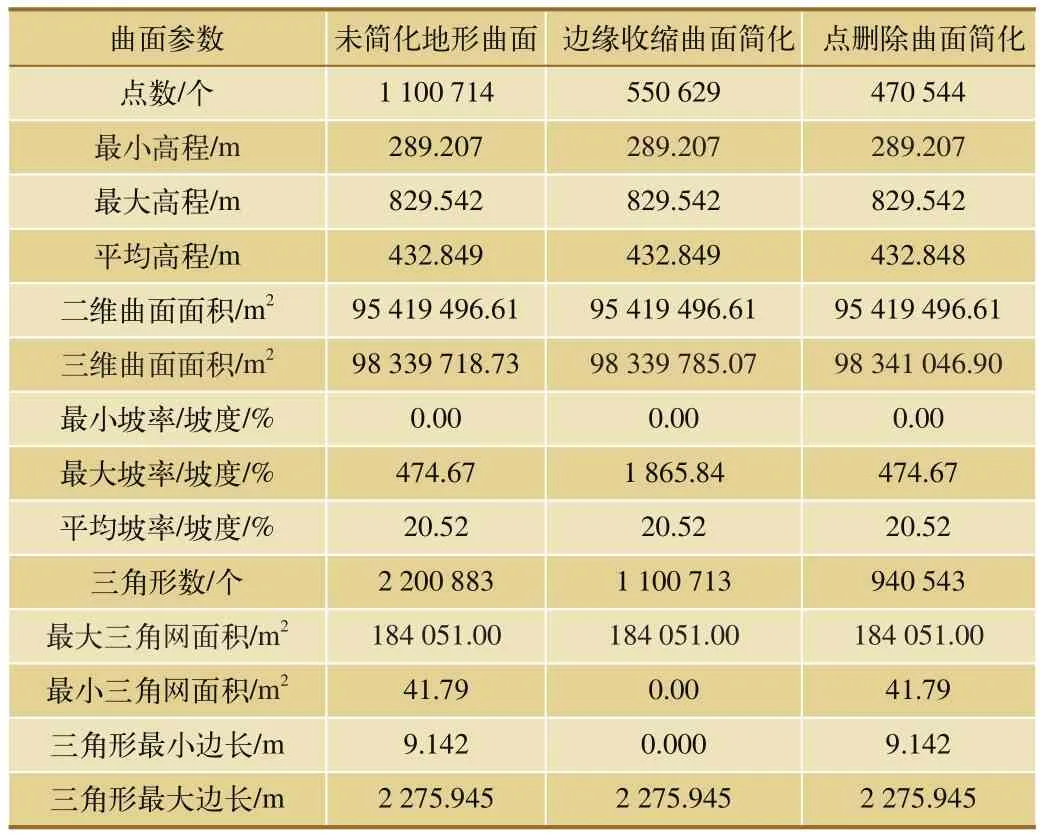
表4 三維曲面不同優化方式參數對比列表

3 結束語

隨著長大線路工程數字信息化程度的提高，項目建設過程中形成的數據種類越來越多，數據量越來越龐大。研究線路工程三維模型的構建方法及有效地輕量化處理方式是線路工程數字信息化變革的技術挑戰之一。本文針對三維地形空間數據的海量特性，通過Delaunay逐點插入算法構建TIN模型，實驗證明該算法能夠用更少的數據來合理地表達復雜地表形態，更適用于線路工程三維地形建模；對比了2種數據輕量化方法，試驗參數對比表明，點刪除法對三維地形模型的簡化更為有效。