一種基于ExtraTrees的差分隱私保護算法

李 楊,陳子彬,謝光強

(廣東工業大學 計算機學院,廣州 510006)

0 概述

隨著計算機存儲數據成本的不斷降低以及云計算、大數據、移動互聯網等技術的廣泛應用和普及,企業、政府組織的信息系統存儲了海量數據,如社交網絡公司的社交數據、各大電商平臺的顧客購買數據以及醫院的病人醫療數據等,這些隱私數據常被用于分析、統計和挖掘。從這些數據中發現潛在的商業價值和規律,同時保證不泄露用戶敏感信息,引起了數據挖掘和隱私保護領域相關學者的廣泛關注。

在早期的相關研究中,數據隱私保護的方法主要是k-anonymity[1]及其擴展模型,如l-diversity[2]、t-closeness[3]和(α,k)-anonymity[4]等。盡管這些模型能夠在一定程度上保護數據中用戶的敏感信息,但是它們的共同缺點是需要假設攻擊者擁有的背景知識和特定的攻擊模型,導致其應用場景受到很多制約。在這種背景下,DWORK C等學者[5-6]在2006年提出具有嚴格理論證明的差分隱私保護模型,該模型為保護數據隱私帶來了一種新的解決思路。在差分隱私保護的定義下,即便攻擊者擁有除目標用戶以外的全部其他信息,用戶仍然能夠防御攻擊并且不會泄露敏感信息。差分隱私保護通過在針對某個數據集上的查詢結果添加噪聲來提供保護,且基于差分隱私保護的算法在輸出結果上添加的噪聲獨立于數據集的規模,添加少量的噪聲能夠保證隱私數據的安全性以及輸出結果的可用性。

目前,差分隱私保護的研究方向集中在差分隱私數據發布[7-9](延伸至社交網絡[10]、軌跡數據[11])、社交網絡研究[12-13]、查詢處理[14-15]以及和數據挖掘相結合(如聚類[16]、分類[17-19]、集成學習[20])等方面,而在回歸分析上的研究則相對較少。進行差分隱私保護回歸分析研究的難點在于求解回歸目標函數的敏感度很大,難以保證回歸準確度。

ExtraTrees作為一種使用頻率較高的集成學習模型,能夠應用于決策樹分類和回歸分析中,本文提出一種基于ExtraTrees的差分隱私保護算法。在決策樹分類上,利用ExtraTrees算法2次隨機選擇的特性,提高指數機制在同等隱私預算下的使用效率,通過將基尼指數作為指數機制在分類樹特征選擇上的可用性函數來降低敏感度,從而減少所添加的噪聲量。在回歸樹上,選擇最佳分裂特征和分裂點時將方差作為指數機制的可用性函數,標記葉子節點時對其均值添加拉普拉斯噪聲。

1 相關工作

1.1 差分隱私的定義

定義1(ε-差分隱私) 設有2個數據集D1和D2,兩者的屬性結構相同,不同的記錄數量為|D1ΔD2|。當|D1ΔD2|=1時,設一個隨機化算法為M,RRange(M)代表算法M的所有輸出構成的集合體,S是RRange(M)中的一個子集,若算法M提供ε-差分隱私保護,則對于所有的S∈RRange(M),有:

Pr[M(D1)∈S]≤exp(ε)Pr[M(D2)∈S]

(1)

其中,Pr[]代表某個事件泄露隱私的概率,其由算法M本身的性質所決定,ε稱為隱私保護預算，是由數據提供者視隱私保護程度所給定的參數,隱私保護程度與ε的取值成反比,ε通常取小于1的常數。式(1)表示對算法M的任何一個輸出結果,不管函數的輸入是D1還是D2,最后得到這個輸出結果的概率差別很小。

1.2 差分隱私保護實現機制

差分隱私保護的實現原理是通過添加噪聲來提供保護,經常使用的2種噪聲模型為拉普拉斯機制[21]和指數機制[22]。某個算法提供差分隱私保護所添加噪聲的多少與全局敏感度有關。

定義2(全局敏感度) 設函數f:D→Rd的輸入為數據集D,輸出為任一實體對象,數據集D1和D2之間不同的記錄個數不大于1,則f的全局敏感度定義為:

(2)

其中,‖f(D1)-f(D2)‖1表示f(D1)和f(D2)之間的1-階范數距離。

定義3(拉普拉斯機制) 對于數據集D上的任一函數f:D→Rd,算法M添加由拉普拉斯分布產生的相互獨立的噪聲變量,以提供ε-差分隱私保護,具體如下:

(3)

定義4(指數機制) 設算法M的輸入為數據集D,輸出為一個具體對象r∈RRange(M),q(D,r)為可用性函數,Δq為函數q(D,r)的敏感度。如果輸出結果滿足式(4),則稱算法M提供ε-差分隱私保護。

(4)

1.3 差分隱私的性質

定義5(并行組合性)[22]設算法M提供ε-差分隱私保護,給定數據集D被切割成互不相交的子集D1,D2,…,Dn,則M作用在{D1,D2,…,Dn}上的組合算法{M(D1),M(D2),…,M(Dn)}具有ε-差分隱私。

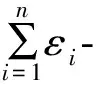
1.4 ExtraTrees算法

ExtraTrees是一種集成學習算法,包含眾多決策樹,分類結果最終由其包含的眾多決策樹的輸出結果共同投票決定,回歸則由這些決策樹輸出值的均值來決定。ExtraTrees算法最大的特點是在分裂特征的選擇上采用隨機的方式,隨機選擇某個特征的某個取值作為該特征的分裂點。由于這2個隨機性特點,使得ExtraTrees算法泛化能力較強,具有抵抗噪聲的能力。

1.5 已有相關研究

在差分隱私保護決策樹分類算法研究中,文獻[24]提出了基于線性查詢函數的分類器算法SuLQ-based ID3。文獻[25]為解決SuLQ-based ID3算法添加噪聲過多的問題,提出一種基于決策樹建造的差分隱私保護算法DiffP-C4.5。文獻[26]沿用數據泛化的思想,在決策樹的基礎上,提出一種非交互式的差分隱私數據發布算法DiffGen。實驗結果表明,在隱私預算相同的情況下,DiffGen的實驗效果相較于其他算法更好。文獻[27]在DiffGen算法的基礎上,通過對細分方案進行改進,為連續型數值加上權重,從而更充分地利用隱私預算,相較于DiffGen具有更好的分類效果。文獻[28]將差分隱私和隨機決策樹模型相結合,提出了RDT算法,但是該算法僅使用拉普拉斯機制,在葉子節點的向量添加噪聲。文獻[29]提出了差分隱私隨機森林算法,該算法的缺點在于僅適合標稱型屬性的數據集,對于包含連續屬性的數據集需要先將連續屬性轉化成離散屬性,然后對數據集進行分類。

在差分隱私保護回歸分析算法研究中,文獻[30]提出了一個利用拉普拉斯機制和指數機制進行統計分析的總體框架,但是該框架要求統計分析的輸出空間有界,導致不適用于線性回歸,并且其直接在計算結果上添加拉普拉斯噪聲,雖然在一定程度上保護了用戶隱私,但是由于添加過多的噪聲,造成計算結果的可用性非常低。文獻[31-32]研究表明,當回歸任務的成本函數是凸函數并且可微時,回歸才能滿足差分隱私保護。相較于文獻[30]直接在輸出結果上添加噪聲,文獻[31-32]在n個目標函數的輸出平均值上添加噪聲以實現隱私保護,其添加的噪聲量有所減少,但該方法普適性較低。文獻[33]為了解決回歸結果誤差大的問題,提出了一種函數機制(Functional Mechanism，FM)。FM機制不是在輸出結果上添加噪聲,而是通過對回歸的目標函數添加噪聲,得到加噪的目標函數,然后求解出最優回歸模型參數。因此,該機制普適性較高,在多種回歸模型上都能應用。但是,由于其計算出來的全局敏感度與數據集的維度成正比,造成噪聲添加過多,使得回歸結果誤差大。文獻[34]提出了一種根據回歸目標函數敏感度大小來分配隱私預算的算法Diff-LR。該算法將線性回歸分析的目標函數拆分成不同的模塊,再分別求解出不同模塊的敏感度。對模塊分配隱私預算時,敏感度大的模塊分派隱私預算多,敏感度小的模塊分派隱私預算少。雖然相對于函數機制FM,該算法有效降低了敏感度,但是其敏感度依然和數據集維度正相關,導致在數據集維度較大的情況下帶來過多的噪聲。

2 DiffPETs算法的框架描述與分析

本文提出一種基于ExtraTrees的差分隱私保護算法DiffPETs,并將其應用于決策樹分類和回歸分析。

2.1 算法描述

DiffPETs差分隱私算法偽代碼如下:

算法1DiffPETs(D,A,Pε,t,h)

輸入數據集D,特征集A,總隱私預算Pε,產生決策樹的個數t,單棵樹的高度h

輸出滿足ε-差分隱私的學習器T={T1,T2,…,Tt}

3.for i = 1 to t:

4.從D中有放回地隨機抽樣大小為|D|的訓練集D(i)

5.調用算法2生成樹Ti=Build_DiffPET(D(i),A,ε2,1)

6.end for

7.返回提供ε-差分隱私的學習器T={T1,T2,…,Tt}

算法2Build_DiffPET(D,A,ε,h)

輸入數據集D,特征集A,隱私預算ε,單棵樹的高度h

輸出滿足ε-差分隱私的學習器Ti

終止條件節點全部記錄的標簽一致,誤差達到閾值或樹達到最大高度h

1.if節點達到了終止條件:

2.返回葉子節點ND=Noise(|D|)

3.end if

5.從K個特征中分別隨機選擇K個分裂點{s1,s2,…,sK}

6.從K個特征和分裂點中,使用指數機制用以下概率選擇最優特征和分裂點:

其中,q(D,A′)表示可用性函數,Δq為可用性函數的敏感度.

7.根據最佳分裂特征和分裂點將當前數據集分割成2個子集Dl和Dr

8.在最佳分裂特征和分裂點的基礎上分別建立左右子樹tl=Build_DiffPET(Dl,A,ε,h+1),tr=Build_DiffPET(Dr,A,ε,h+1)

9.返回提供ε-差分隱私的學習器Ti

算法1展示了DiffPETs的基本框架,其涉及5個主要的輸入參數:數據集D,特征集A,隱私預算Pε,產生決策樹的數目t和單棵樹的高度h。DiffPETs首先根據生成決策樹的數量t和樹的高度h將隱私預算Pε進行分配(第1～第2行),然后根據生成決策樹的數量t循環建立單棵決策樹,每次建立單棵決策樹時使用不同的抽樣樣本,以提高算法的泛化能力(第3～第6行)。算法2展示了生成單棵決策樹的詳細步驟,首先根據如下規則判斷當前節點是否達到終止條件:1)分類樹上節點所屬記錄的分類特征是否相同;2)回歸樹上節點誤差是否小于閾值;3)樹是否達到最大高度h。當滿足終止條件以后,使用拉普拉斯機制返回添加了噪聲的葉子節點(第1～第3行),然后從特征集A中隨機選擇K個特征和分裂點,使用指數機制選擇最佳分裂特征和分裂點(第4～第6行)。本文指數機制的選擇方法為:將算法2第6行計算出的各概率值按順序排列放在坐標軸上,分別對應0～1上的某個區間,之后隨機生成一個0～1之間的數,隨機數對應哪個區間,指數機制就挑選相應備選項作為輸出。最后,根據最佳分裂特征和分裂點遞歸構造左右子樹,返回單棵決策樹Ti(第7～第9行)。

2.2 算法隱私性分析

DiffPETs算法首先將總隱私預算Pε平均分配給每一棵決策樹ε1=Pε/t。根據差分隱私的性質[22],由于單棵樹的樣本有交集,因此算法耗費的隱私預算為單棵決策樹耗費隱私預算的總和,然后按照同樣規則遞歸產生每一棵決策樹。具體步驟如下:首先從D中有放回地抽取大小為|D|的訓練集D(i),隨后將單棵樹的隱私預算平均分配給各層ε2=ε1/(2(h+1)),每層的隱私預算平均分成兩部分,一部分應用拉普拉斯機制對劃分到該節點的樣本數添加噪聲,然后判斷是否滿足終止條件,若滿足則將此節點標記為葉子節點,若沒有達到終止條件,隨機地從|A|個特征集中選擇K個特征,之后再隨機產生K個分裂點,利用指數機制和剩余的隱私預算選擇最佳分裂特征和分裂點。因此,算法所耗費的全部隱私預算是Pε,提供ε-差分隱私保護。在分類中,指數機制中的可用性函數為基尼指數,而在回歸中其可用性函數為方差。

2.3 敏感度分析

2.3.1 基尼指數的敏感度

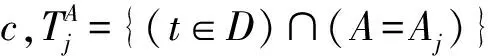
(5)

(6)

2.3.2 均值的敏感度

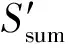
2.3.3 方差的敏感度

決策樹方差的定義如下:

(7)

3 實驗結果與分析

本文分類器訓練算法、測試算法和數據處理均通過Python3.5版本實現,無差分隱私的算法調用scikit-learn庫實現。硬件環境為Intel(R)Core(TM)i5 2.5 GHz,內存為8 GB 1 600 MHz DDR3。為檢驗DiffPETs算法的性能,采取如下5個UCI公開數據集進行實驗:1)Mushroom數據集,根據蘑菇的各種特征預測蘑菇是否可以食用;2)Nursery數據集,根據家庭背景等特征預測申請幼兒園的等級;3)Congressional Vote Records(CongVote)數據集,美國國會投票記錄,預測共和黨或民主黨是否能夠當選;4)WineQuality數據集,根據物理化學特性預測紅葡萄酒的質量;5)Daily_Demand數據集,預測巴西某一家物流公司訂單的總量。表1所示為5個數據集的基本信息。

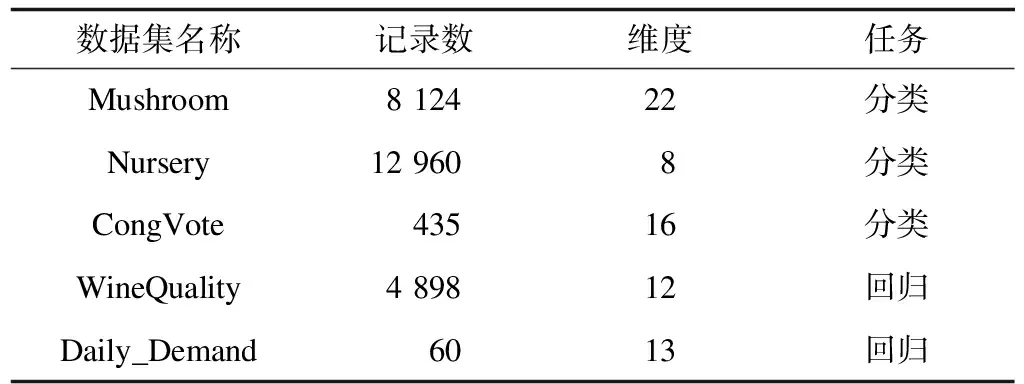
表1 實驗數據集信息

3.1 分類實驗結果

為驗證DiffPETs算法在分類預測中的性能表現,分別令ε={0.50,0.75,1.00}(其對應森林中樹的個數分別為t={10,10,5}),設置每棵樹的高度為h=k/2,k為對應數據集的維度,可用性函數為基尼指數。本文首先利用DiffPETs算法在訓練集上生成算法模型,之后在不同的隱私預算、樹的棵數和單棵樹的高度下進行實驗,最后在測試集上作預測,并計算相應的準確率。每組實驗進行10次,以平均實驗結果作為最后的準確率,將DiffPETs算法與無差分隱私、RDT[28]和DiffPRF[29]算法進行比較,實驗結果如圖1～圖4所示。

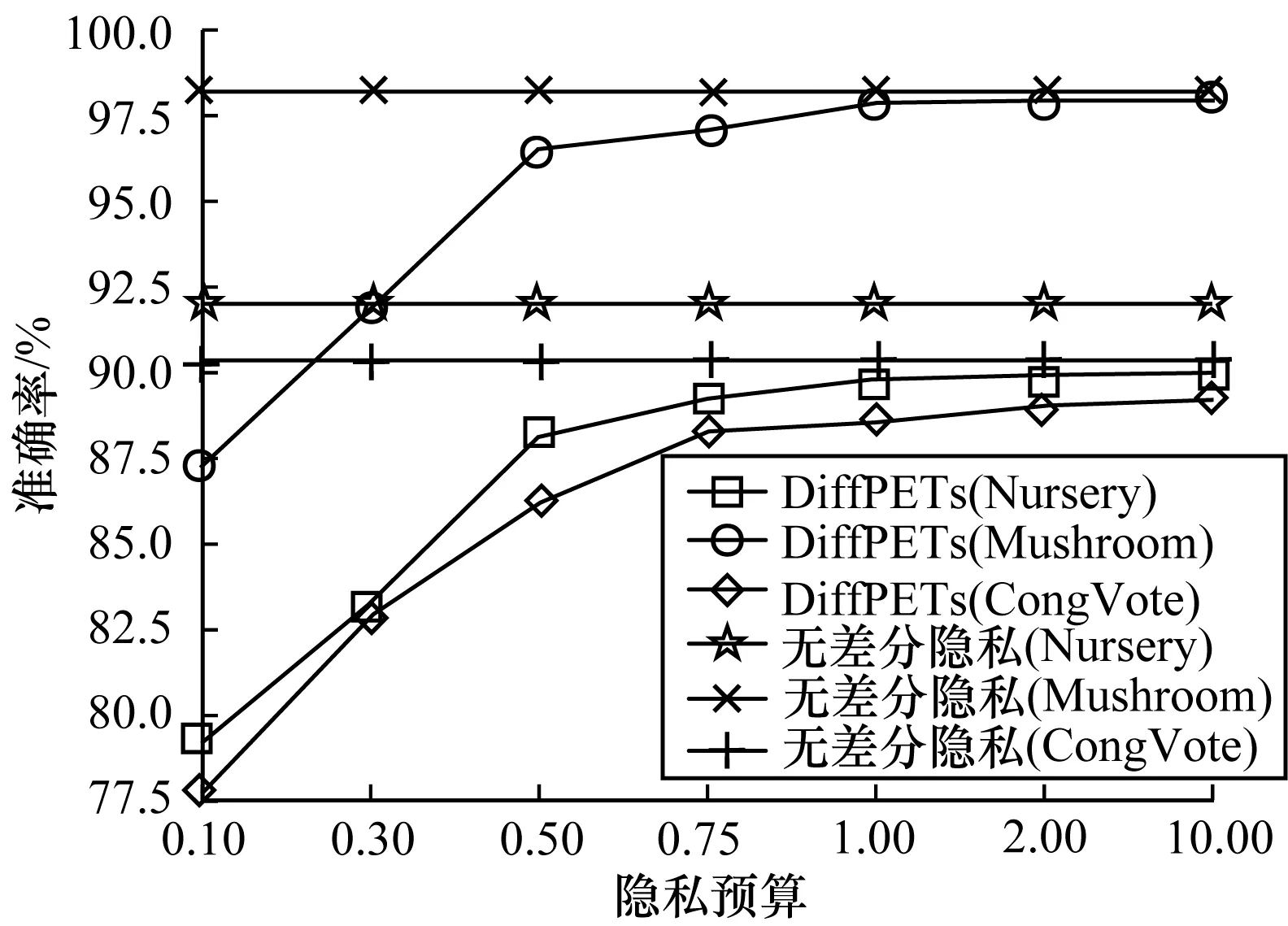
圖1 不同隱私預算下的分類結果

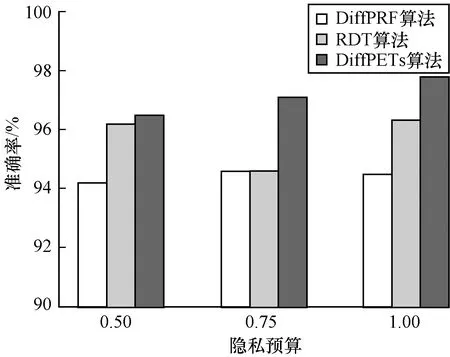
圖2 Mushroom數據集在不同隱私預算下的實驗結果

Fig.2 Experimental results of Mushroom dataset under different privacy budgets

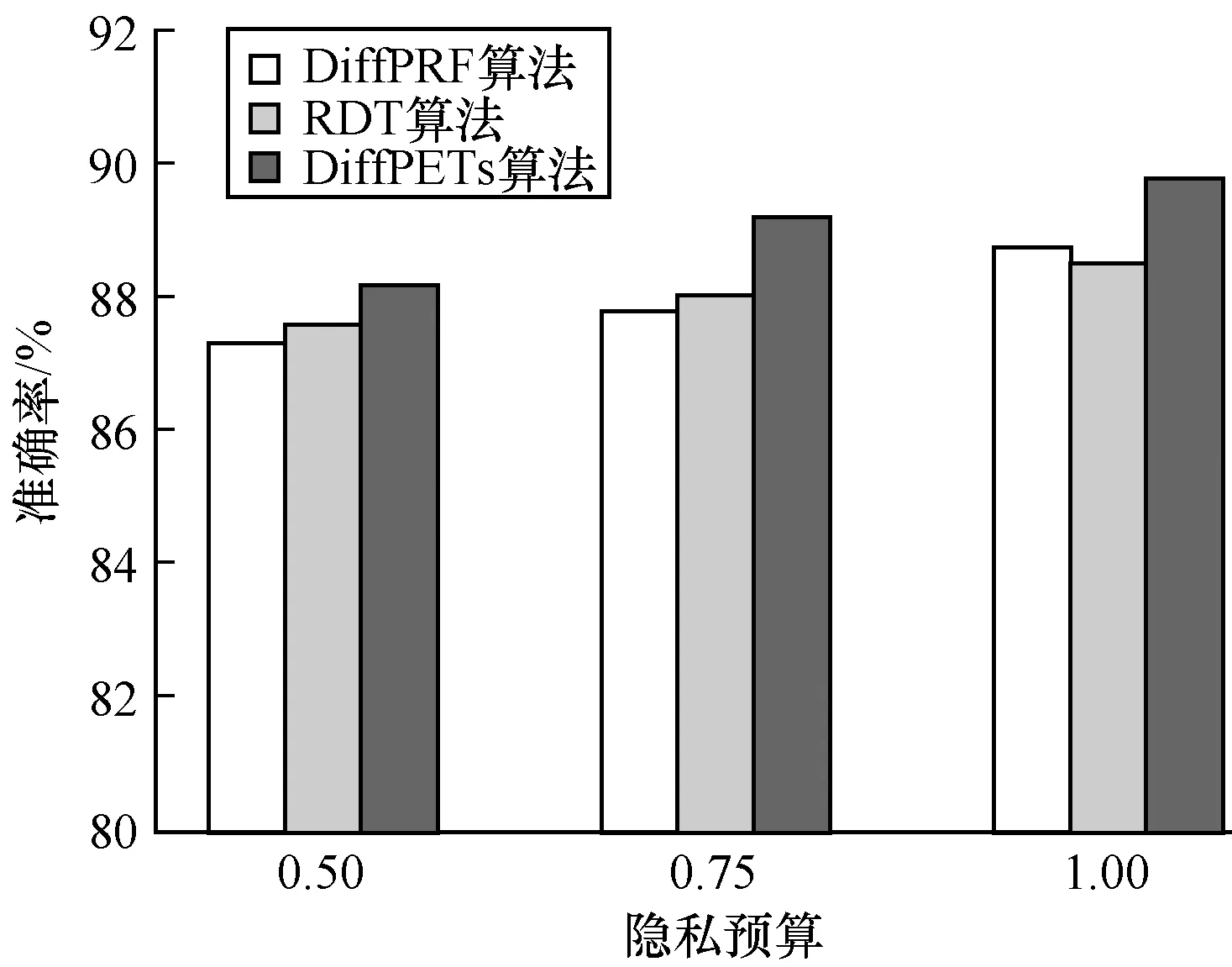
圖3 Nursery數據集在不同隱私預算下的實驗結果

Fig.3 Experimental results of Nursery dataset under different privacy budgets

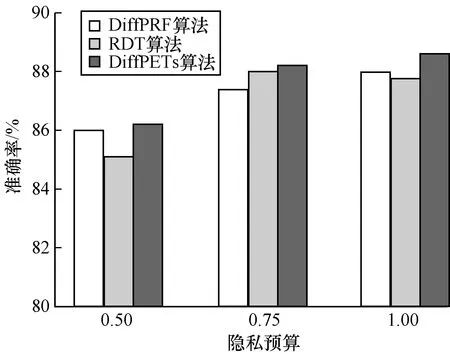
圖4 CongVote數據集在不同隱私預算下的實驗結果

Fig.4 Experimental results of CongVote dataset under different privacy budgets

從圖1可以看出,在隱私預算較小時,DiffPETs算法的準確性不高,可以理解為為了實現高級別的隱私保護,算法不得不做出一些犧牲。隨著隱私預算的增加,DiffPETs算法的準確率逐漸提高,原因是添加到算法中的噪聲量逐漸減少。通過與DiffPRF和RDT算法進行對比可以看出,本文算法在同等隱私預算下能夠實現較低的分類誤差。

3.2 回歸實驗結果

在回歸實驗中,本文采用均方誤差(MSE)來判斷算法的性能,其定義如下:

(8)

和分類實驗一樣,令ε={0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0},森林中對應樹的個數為t=10。每組實驗重復10次,采用最后的平均誤差為實驗結果,并將本文算法與無差分隱私、FM[33]、Diff_LR[34]算法進行比較,實驗結果如圖5、圖6所示。

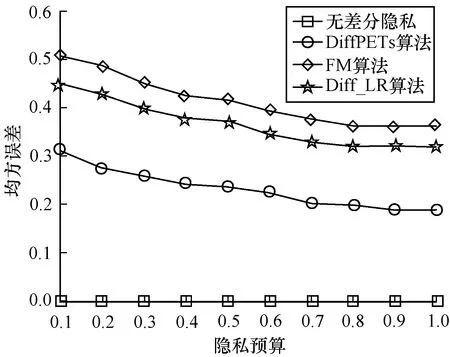
圖5 WineQuality數據集的均方誤差

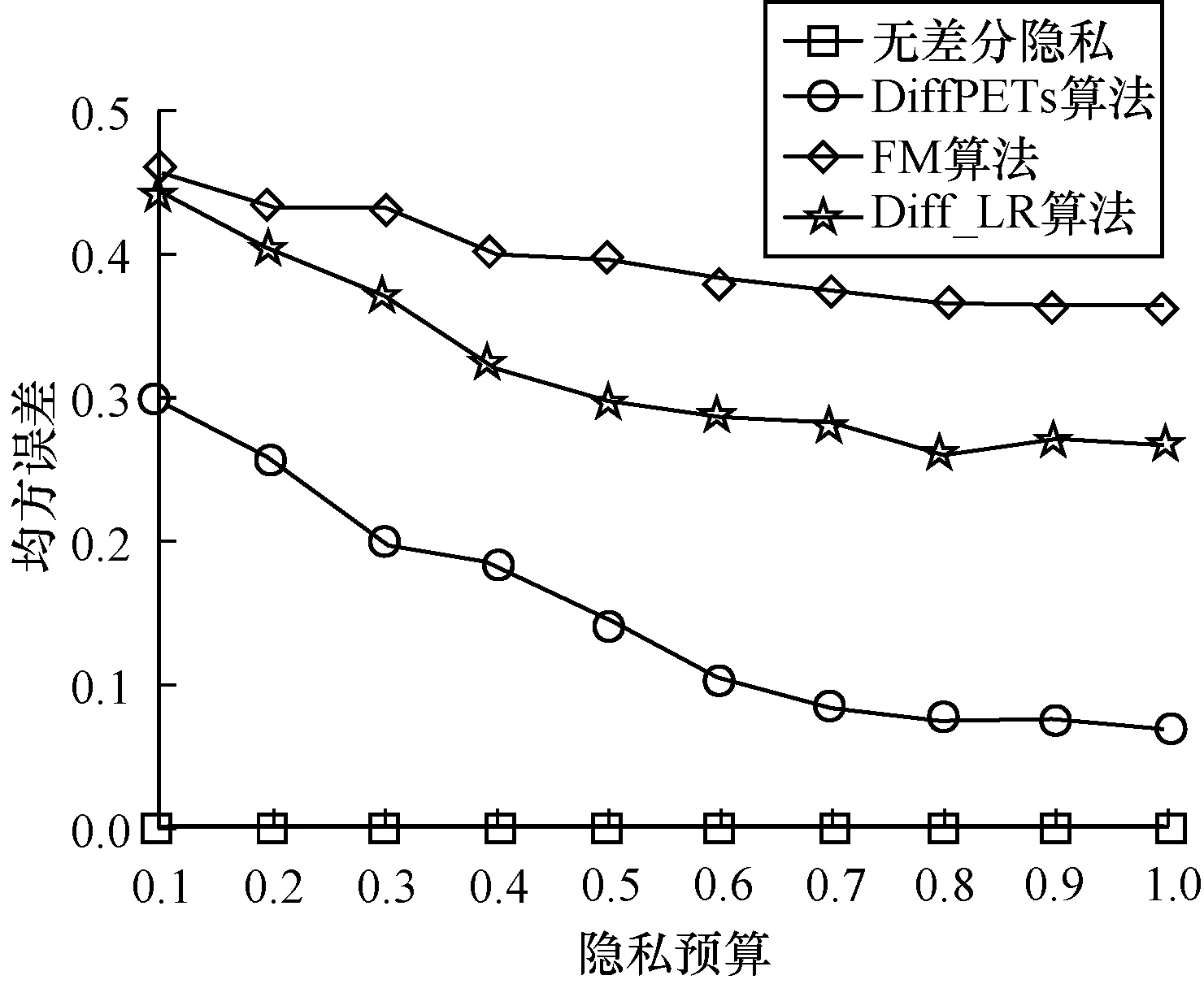
圖6 Daily_Demand數據集的均方誤差

從圖5、圖6可以看出,在同等隱私預算ε的條件下,本文DiffPETs算法相比于FM和Diff_LR均方誤差更小。隨著ε的增加,DiffPETs算法的均方誤差與未加噪聲的模型逐漸接近。此外,可以看出,沒有添加噪聲的模型產生的均方誤差與隱私預算ε的大小無關。

4 結束語

本文提出一種基于ExtraTrees的差分隱私保護算法DiffPETs,并將其應用于分類和回歸分析。在決策樹分類時,采取隨機的方式選擇特征使算法的泛化能力得到有效提升。在回歸中,算法的全局敏感度與所添加的噪聲均較低,回歸預測的結果更準確。實驗結果表明,DiffPETs算法具有較高的可行性與準確性。下一步考慮將本文算法應用于交通、醫療等大數據問題。