基于時間交互偏置影響傳播模型的弱連接重疊社區檢測
許小媛,黃 黎,李海波
(1.江蘇開放大學 信息工程學院,南京 210017; 2.南京航空航天大學 計算機科學與技術學院,南京 211106)
0 概述
目前,社交網絡已經成為人們日常生活的重要組成部分,如臉譜網、Twitter和LinkedIn等。約68%的在線用戶擁有社交信息,用以獲取新聞或與其他人進行聯系,大量用戶加入到在線社區中,使得社區檢測成為社會網絡挖掘領域中的一項熱門工作[1-2]。社區內的用戶之間具有緊密的連接關系,社區檢測指在給定網絡中對所有社區進行識別,其具有較多重要的現實應用,包括有效的信息傳播、目標市場識別和感染控制等[3]。
傳統的社區檢測方法,如Louvain方法、infomap方法、標簽傳播或Newman主要特征向量方法等[4],主要關注用戶之間的關系連接,采用連接關系強弱量化指標。這些方法將網絡表示為具有穩定連接的靜態結構,原因是這些連接將持續很長時間。文獻[5]基于Louvain方法提出一種不相交重疊社區檢測方法,其考慮具有可接受時間成本的社會網絡中的圖分割過程實現方式。文獻[6]引入加權社區聚類度量,采用infomap指標實現了大規模圖社區模型的可擴展社區檢測,該指標的設定依賴于社區中的三角結構。文獻[7]基于標簽傳播算法模型,采用PageRank方法,提出一種大規模社區檢測過程中解決處理器負載均衡問題的方法。文獻[8]基于Newman主要特征向量方法將社區檢測過程優化為一個NP難優化問題,然后采用啟發式搜索算法實現對社區結構的有效檢測。上述算法均取得了良好的效果,但是,在Twitter數據集中的實驗結果表明,多數用戶不依賴他們的用戶關系連接進行交互操作。
社區邊緣攜帶的關系可提供更有意義的信息,并更準確地反映關系的強度,這些關系可以通過邊緣權重的分配來量化,從而提升社區的時間交互測量性能。在社區信息提取中關注動態結構而非靜態結構,能提高聚合性度量的準確性并識別出更有意義的社區。
本文研究動態加權圖模型社區檢測問題,通過預測有影響力的用戶未來的活躍趨勢,構建一種影響傳播模型,以確定用戶的高頻率相互作用并度量其對鄰近用戶的影響。同時,為提高社區檢測的準確率,針對圖社區劃分過程引入一個目標函數,并行處理這些分區劃分過程以求解影響傳播模型。在此基礎上,提出一種時間交互偏置(TIB)社區檢測方法,以對重疊社區進行檢測。
1 問題描述
本文研究一個加權無向簡單圖G=(V,E,W),其中,V表示節點集合,E表示邊緣集合,W是權函數集,ω∈W[8-9]。針對每個邊e=(u,v)?E,權重w(e)=∑(IInteractions)≥0表示隨機選擇的時間間隔為t的節點u和v之間相互作用的總頻率。例如,在Twitter數據集中,權重為w(e)=∑(@+IRTs),其表示在給定時間間隔t內交互作用的總和,@表示上一時刻交互作用總和,IRTs表示當前時刻的交互作用。表1所示為本文相關數學符號的定義。

表1 數學符號定義
問題1(時間交互偏置問題) 尋找社區C(V,E,W)?G,其為k個連通群落集,使得:1)?e∈E,其中,e是活躍或者半活躍邊;2)活躍偏密度度量指標ρ(C)最大化。
為求解連接的k群落約束,首先給出clique的定義:clique是一個完全連通的子圖,PC是相鄰clique集,這意味著兩者共享k-1個節點。例如,對于k群落,如果k=3可視為三角形,則k=3情形下的PC可以被可視化為連接三角形。
在已有研究中,邊緣的相關性權重表示網絡邊緣的活躍程度。在Twitter網絡中,邊緣加權為40,意味著它含有40個交互過程,并且很可能被視為活躍邊緣。但非活躍邊緣也有可能是重要邊緣,比如其多數鄰居是高度活躍邊緣的情況。本文定義了一個鄰居頂點的活躍邊緣,稱為偏置活躍邊緣。在以往研究中,邊緣加權值3通常認為是不活躍的,然而,如果其具有活躍鄰居,則它可能成為偏置的活躍邊緣,因為該邊緣將通過傳播這些鄰居的權重來重新定義加權值。
在檢測時間交互偏置的社區檢測背景下,可以認為弱連接邊非常重要。雖然在當前時間間隔中其影響很小,但是在后續社區檢測過程中,其影響可能被放大,即如果它們的鄰域節點高度交互,它們可能在一定時間之后變得活躍。因此,本文提出一種影響傳播模型來解決第1個約束,即e可以是活躍的或接近活躍的邊緣,它決定邊緣的潛在權重并重新定義活躍邊緣。
2 時間交互偏置社區檢測傳播模型
考慮圖的每個邊緣e,本文模型通過2個步驟確定邊緣的權重。第1步基于以下標準對邊緣e的權重w(e)進行歸一化[10-11]:
(1)
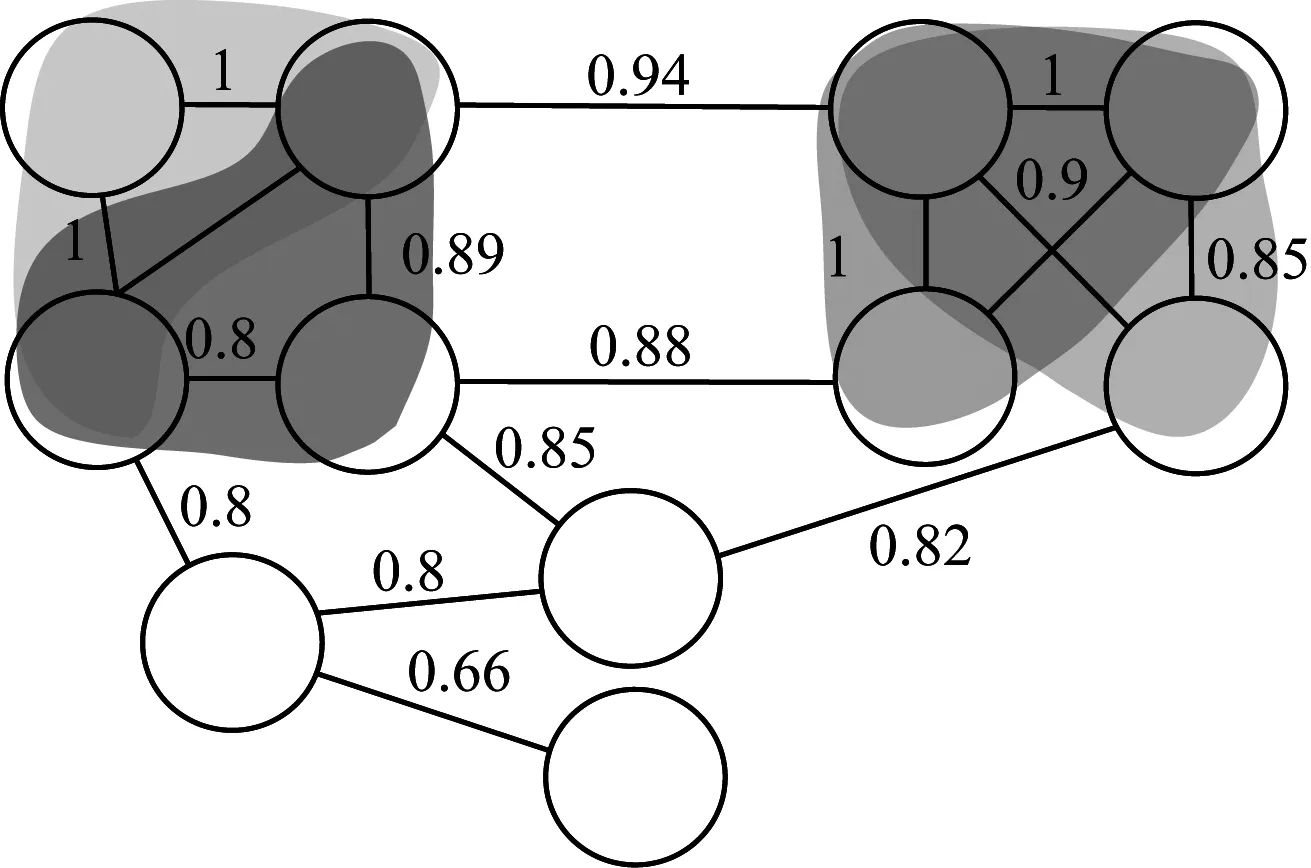
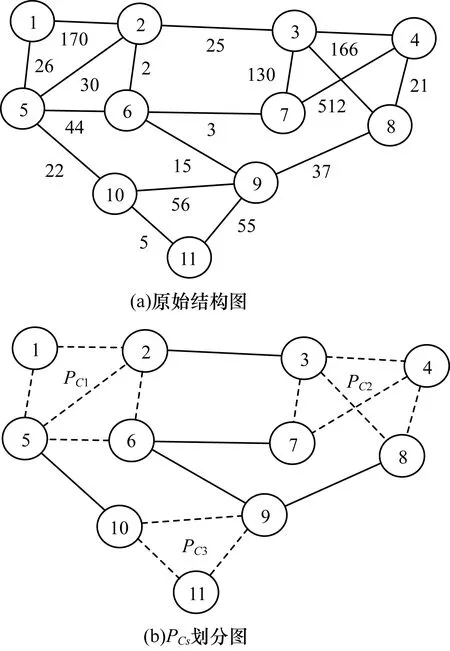
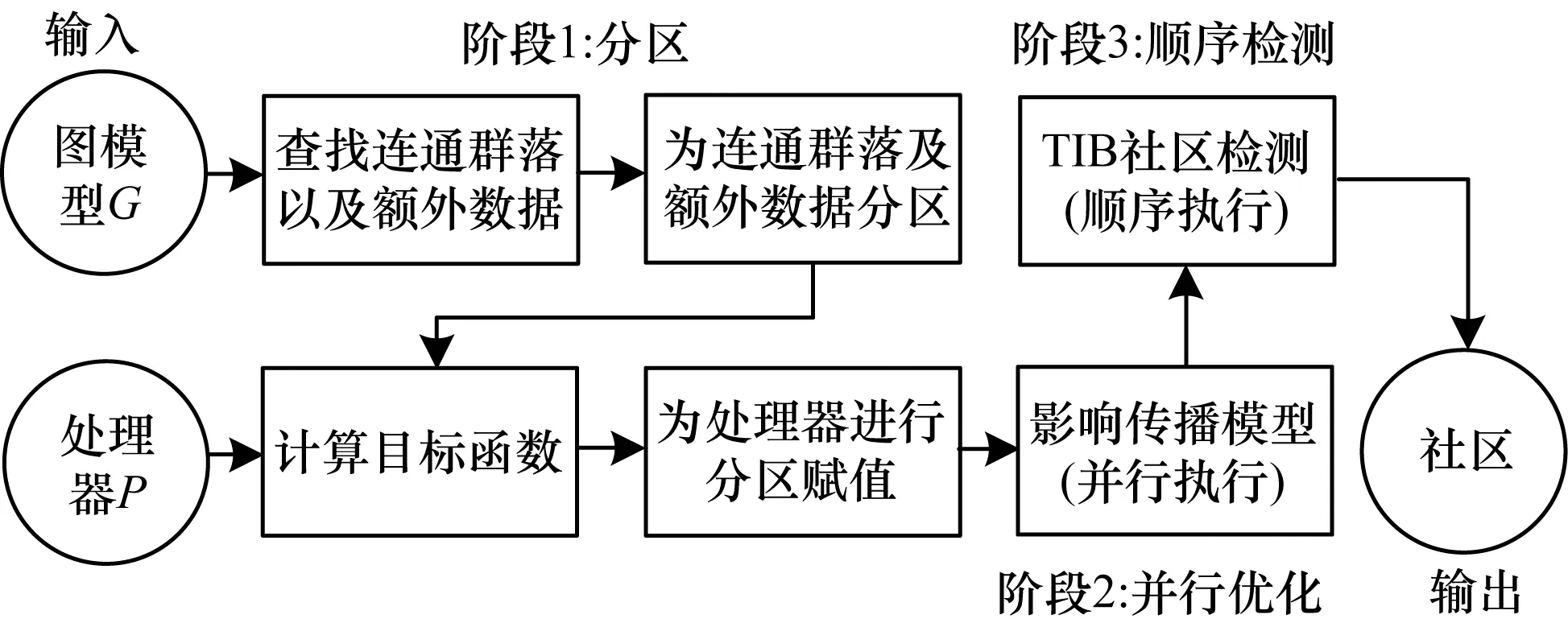
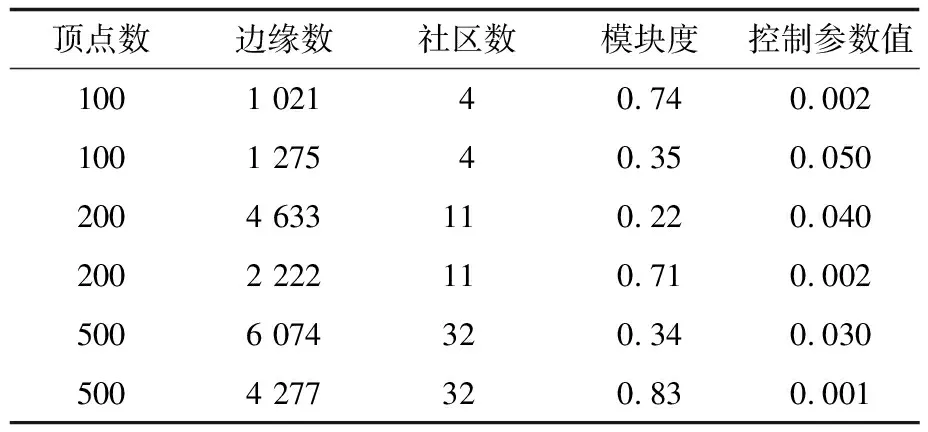
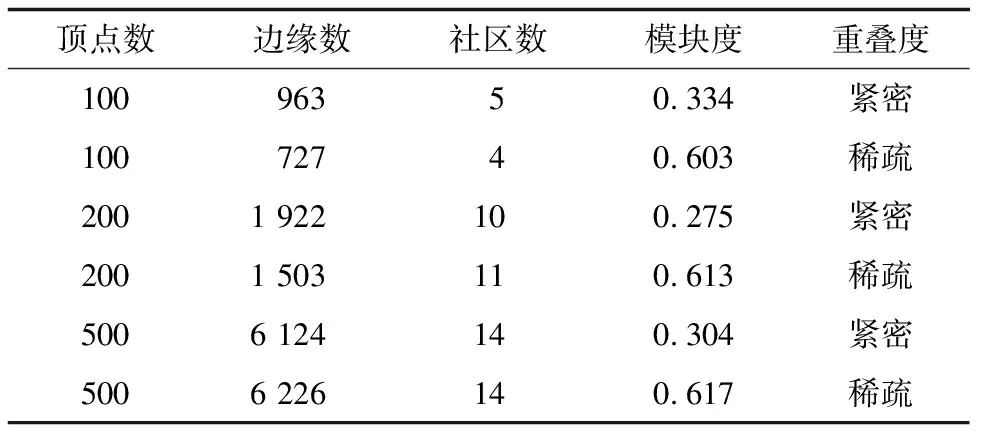
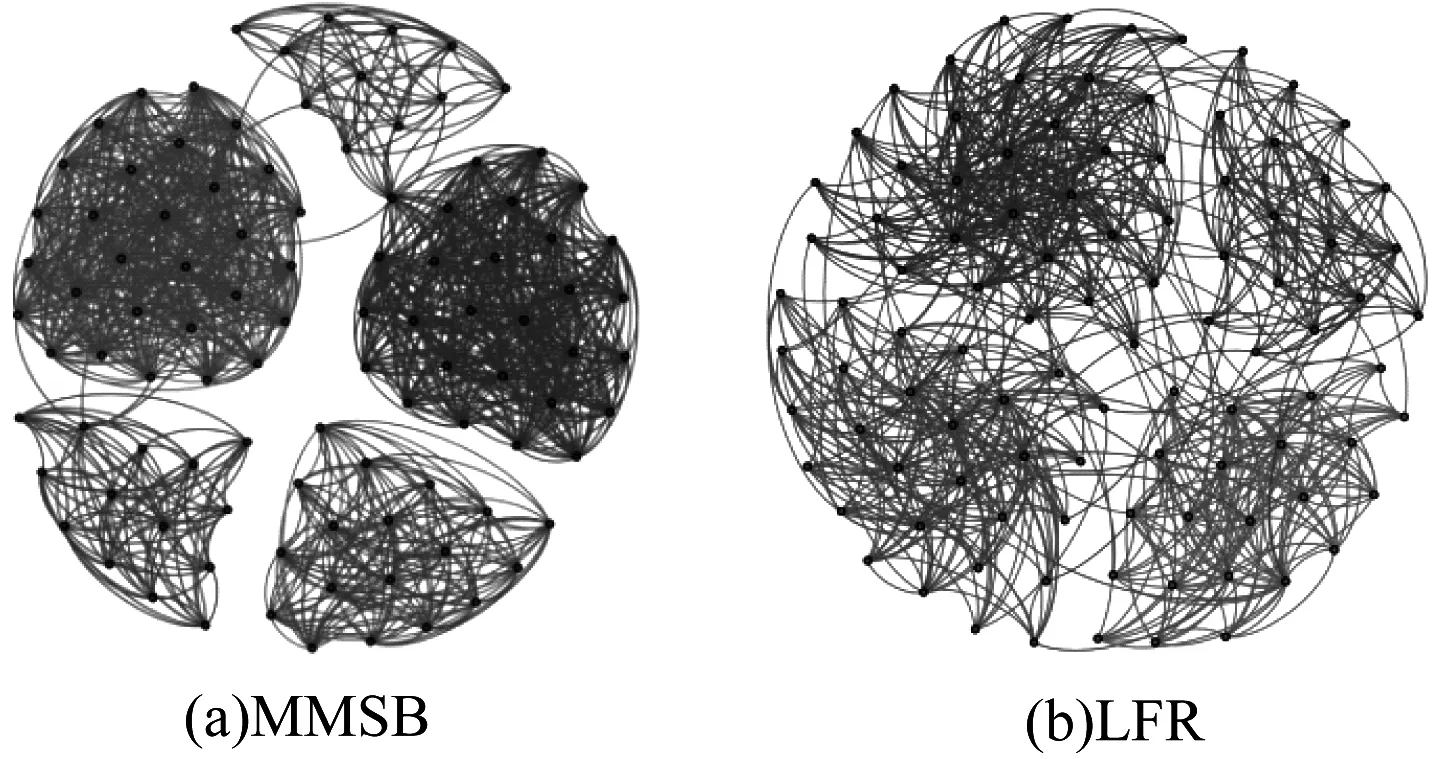
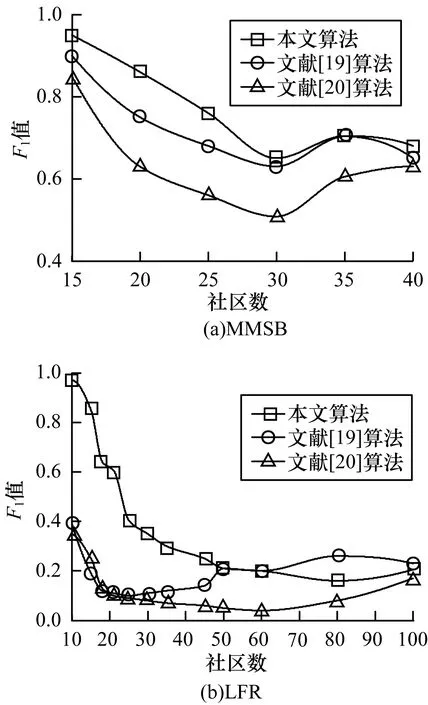
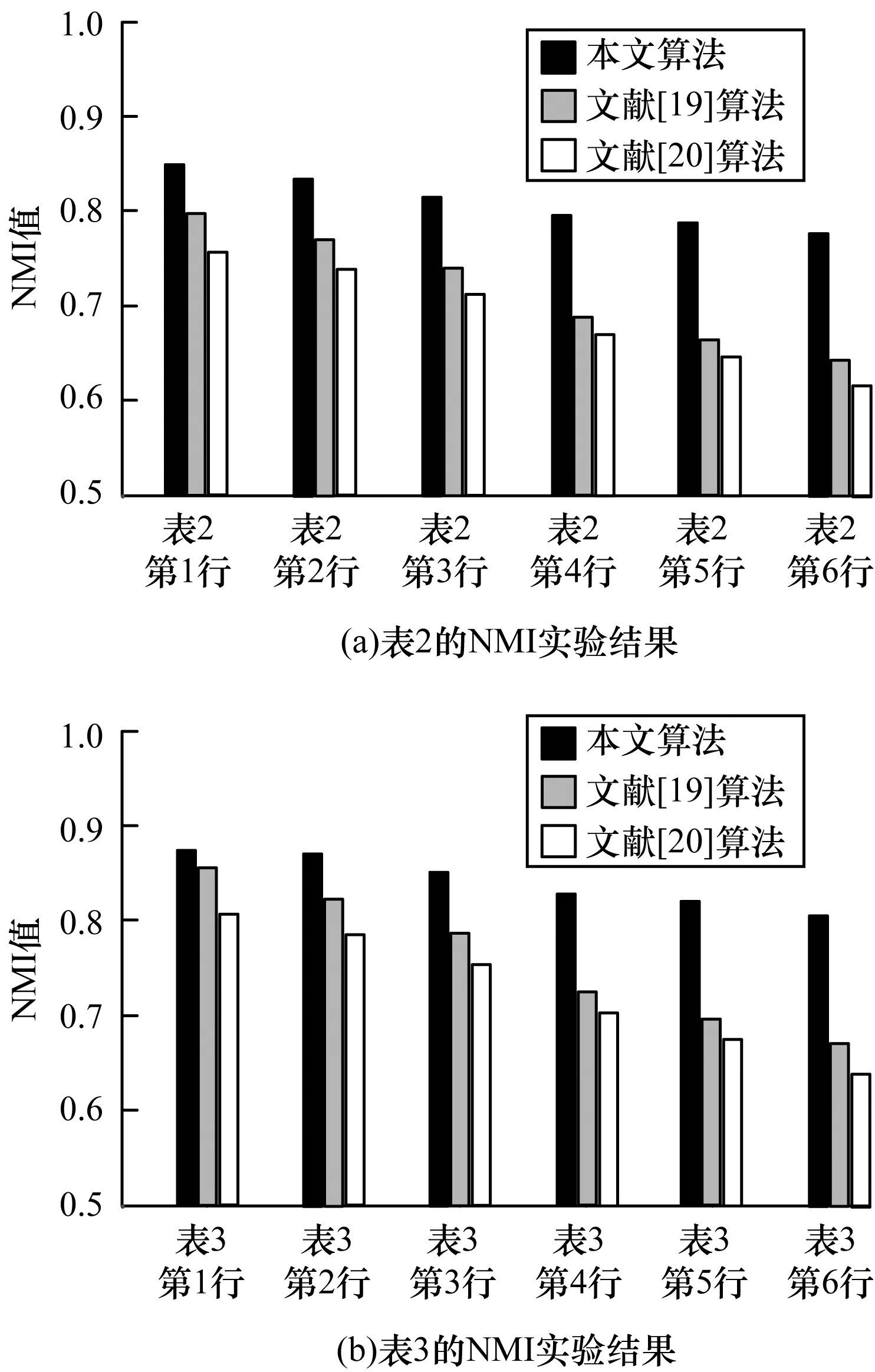
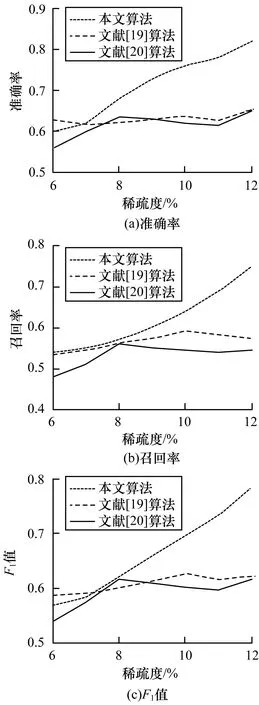
其中,0≤N(e)≤1,非零值參數表示不同的活躍程度。當N(e)=1時,表示邊緣的活躍程度為100%。式(1)中的參數m和n是實數,且滿足m 定義1(活躍邊緣ei) 當N(e)=1時,社區的邊緣ei稱為活躍邊緣[12]。 定義2(近似活躍邊緣) 活躍邊緣ei在h跳內的相鄰邊緣稱為近似活躍邊緣。 本文模型中的第2步是基于活躍邊緣ei向其鄰居節點e傳播歸一化權重,過程如下: U(e)=λh·N(ei) (2) 其中,λ(0<λ<1)是一個衰減因子,h是當前邊緣和其鄰居節點之間的跳數,N(ei)是ei活躍鄰居的權重。對于邊緣ei的h跳內的下鄰域邊緣,重復計算U(e),然后,將U(e)的結果存儲在一個散列表中,該散列表被用來計算邊緣e的最終權重f(e),表示為[13]: (3) f(e)將哈希表中的值相乘,以確定邊緣e的新權重。 該學習模型考慮邊緣的鄰居節點,有助于基于鄰居的活躍度來重新定義邊緣權重。此外,通過非活躍邊緣的相鄰邊緣權重來計算時間交互的邊緣權重,因此,其不僅考慮當前時間間隔,而且關注相鄰邊緣的影響概率。 示例1考慮圖1所示的具體示例,其中,線上數字表示權重,方框中數字表示歸一化權重。圖1(a)所示為原始加權圖。利用N(e)從0到1重新定義權重,當執行式(3)(?e∈E∧N(e)≠1)時,將結果存儲在哈希表中,如圖1(b)所示,此處省略了一些細節以避免混亂。使用哈希表來計算每個邊的最終權重,如圖1(c)所示,其中,采用f(e)進行計算。本文考慮k群落的基本定義以檢測重疊社區。 圖1 權重賦值示例 定義3(活躍偏置密度) 活躍偏置社區的密度指標可表示為: (4) 活躍偏置社區的密度為社區內權重的總和除以社區的大小|C|,可基于閾值限制群落來評估社區的質量。因此,基于C群落可進行社區發現,其中,ρ(C)可實現最大化。 示例2考慮圖2所示的示例,設有一個重構的加權圖,在圖中找到所有的群落并利用式(4)計算它們的偏置密度值。然后,利用式(4)計算PCs的偏置密度值,結果如圖中線上數字。PCs僅在其偏置密度得分高于每個社區的偏置密度分數時形成一個社區;否則,每個群落本身就是社區。圖2給出2種情況:左側的2個PCs在聯合時具有較小的密度值,右側部分是交互作用情況。顏色深淺表示密度值大小。 圖2 社區偏置密度值 問題2(基于群落的圖劃分) 查找社區集R,其中,?r∈R包含2個約束:1)節點和邊屬于群落結構;2)分布在處理器組(P)上的均衡數據(節點和邊緣)負載。 上述問題中的第2個約束是對處理器上的分區進行平衡,并確保每個處理器具有可接受的數據量。該問題是NP難問題,可采用啟發式算法進行求解。本文分配每個PC到一個分區,分區數量等于處理器的數量,每個分區將被分配給處理器。 定義4(目標函數J) 如果滿足如下3個條件,可將PCs均勻分配到可用分區:1)分區R的數量大于處理器P的數量,即R≥P;2)每個分區r∈R?G具有幾乎相同數量的PCs;3)目標函數J取值最小。 為滿足上述3個條件,為每個未賦值的參數pc∈PCs進行如下的賦值計算: (5) (6) (7) 示例3考慮圖3(a)所示的示例。為對該圖進行分割,首先找到群落然后查找PCs,其中,PCs見圖3(b)虛線部分所示。假定處理器數量P=2,需要2個分區,每個處理器分配一個分區。為將3個PCs盡可能均勻地劃分為2個分區,需要計算目標函數J。首先將PC1分配給分區1,將PC2分配給分區2,而對于PC3的分配,將根據目標函數J的取值進行設置。當添加PC3到分區1中的PC1時,目標函數J的計算結果為54。當添加PC3到分區2中的PC2時,目標函數J的計算結果為44。基于該計算結果,PC3的分區方式將采取后一種情形,將其分配給處理器2。 圖3 PCs圖分割過程示例 圖4所示為本文算法框架,該算法分為3個階段:1)基于PCs和目標函數J進行圖分割,此處不屬于群落的節點和邊緣將被消除;2)計算每個分區的影響傳播模型;3)利用TIB社區檢測方法檢測社區。算法開始時,輸入社區檢測的圖模型G=(V,E,W),并給定處理器的數量,輸出是社區劃分集。 圖4 本文算法框架 本文社區檢測算法各階段的詳細過程如下: 1)圖分割,該過程的計算步驟如算法1所示。算法輸入是無向加權圖、鄰域跳數以及處理器P的數目。首先,查找群落(第1行)和PCs(第2行)。然后,收集PCs中每個邊緣h跳范圍內的鄰域節點(第3行~第7行),以計算影響傳播模型。接著,分配一些PCs到分區,如果有6個分區,則分配6個PCs(第9行)。隨后,基于目標函數J的計算結果,將剩余的PCs分配到分區中(第10行~第13行)。當所有PCs在分區上被平均分配時,算法的分區劃分過程結束(第14行~第15行)。 算法1圖分割算法 1.輸入:G(V,E,W),hops,P 2.C←FindCliques(G); 3.PC←FindPercolatedCliques(C); 4.h←1; 5.for e∈PCand h 6.NP←FindNeighbours(e); 7.h←h+1; 8.end for 9.repeat 10.將n個PCs分配給n個處理器Ps; 11.if PCi未賦值給Pithen 12.J(Pi,PCi+n); 13.將具有最低評估值的PCi賦值給Pi; 14.end if 15.until 所有PCs賦值給Pi; 16.return P集合 算法2影響傳播模型計算算法 1.輸入:集合P 3.for all e∈E do 4.P(e)←w(e); 5.end for 6.for 所有e滿足P(e)<1 do 7.h←1,N←{ }HashTable={ }; 8.while h<4 do 9.N←FindNeighbours(e); 10.HashTable←U(e); 11.h←h+1; 12.end while; 13.end for 14.for all U(e)∈HashTable do 16.end for 3)TIB群落檢測。該過程計算算法輸入為社區圖模型G=(V,E,W),算法基于連通群落識別重疊的社區結構。如圖2(a)所示,首先獲得一組不能進一步擴展到超出大小k的所有最大群落。在文獻[10]中,考慮共享k-1個節點的所有相鄰群落,群落選取的標準是密度指標I(G)大于閾值θ,I(G)計算如下: (8) 該函數允許k群落包含比閾值弱的連接,因此,所產生的社區包含強度大于I的k群落。 TIB群落檢測的計算過程如算法3所示。本文采用前述ρ(C)指標替代I(G)進行算法設計,偏置密度測量指標可找到不一定相連的TIB社區群落。然后,計算PCs的密度值ρ(C)并作為最大可達的k群落(第3行~第8行)。同時,計算ρ(pli),?pli∈PL,通過密度比對確定最終的TIB社區識別結果(第9行~第17行)。 算法3TIB群落檢測算法 2.CL←{ },PL←{ }; 3.CL←FindClique(G,k); 4.for all cli∈CLdo 5.D←ρ(cli); 6.if cli∪cl(i+1)do 7.PL[pli]←cli∪cl(i+1); 8.D←ρ(pli); 9.end if 10.for all cli∈pcido 11.if D[pli]≥D[cli]do 12.C←pli; 13.else 14.C←cli,cl(i+1); 15.end if 16.end for 17.end for 18.return TIB社區集C={C0,C1,…} 本文選取的社區檢測質量評價標準為標準化互信息(NMI)評價指標和F1評估指標。NMI可評估檢測社區的相似性,F1可對社區檢測精度進行評估。 本文選取的實驗對象生成方法是MMSB和LFR,具體生成策略可見文獻[14]。根據網絡參數的設定,對生成網絡的稀疏程度進行調整,以獲得不同特性的網絡,具體如下: 1)MMSB對象生成方法:該社區生成方法的基礎是概率理論,得到p和q間的社區連接,其具有Y(p,q)分布特性[15]: (9) 其中,參數β為社區檢測過程中所使用的交互矩陣,Z為社區檢測過程中所呈現出的分布形式,其具有多項式特性[16]: (10) (11) 其中,參數α的作用是對生成模型社區的重疊度進行控制。根據實驗結果,如果要獲得稀疏的重疊社區網絡模型,可將模塊度指標調整為大于等于0.5;反之,如果要獲得稠密的重疊社區網絡模型,可將模塊度指標調整為小于0.5。表2所示為采用MMSB方法生成的網絡實驗對象的屬性數據。 表2 采用MMSB方法生成的網絡對象屬性 2)LFR對象生成方法:該社區網絡生成方法同MMSB對象生成方法相似,可基于模塊度參數的設置控制社區網絡模型的稀疏度,其參數設定如表3所示。 表3 采用LFR方法生成的網絡對象屬性 圖5所示為實驗對象模型結構,其中,圖5(a)、圖5(b)分別對應表2的第1行和表3的第3行參數。 圖5 實驗對象模型結構 利用F1評價指標對社區發現過程進行質量評估,其指標形式為[17-18]: (12) 其中,參數FP是真實網絡中為正值但社區檢測結果為負值的比例,參數FN是真實網絡中為負值但社區檢測結果為正值的比例,參數TP是真實網絡中為正值且社區檢測結果為正值的比例,P表示社區檢測的準確率,R表示社區檢測的召回率。 為驗證算法的有效性,本文選取文獻[19-20]中的2種重疊社區檢測算法作為對比。F1評估指標實驗結果如圖6所示。在通常情況下,F1評估結果取值區間在0~1之間,該指標取值越大,表明算法的穩定性越高。從圖6可以看出,本文算法的F1值優于文獻[19-20]2種對比算法,這表明本文算法的社區檢測穩定性更優。同時,在F1評估實驗結果的變化趨勢上,3種對比算法均隨著社區數量的增加而呈現出逐漸降低的趨勢,這說明3種算法在進行社區檢測的過程中,其穩定性與社區數量存在一定的關聯性,社區數量越多,算法穩定性越差。 圖6 3種算法的F1測試結果對比 對算法的社區檢測準確性進行實驗分析,選取NMI作為評估指標。對于社區A和B,NMI具體定義為: (13) 其中,參數N表示社區檢測網絡中的頂點數,參數C表示社區檢測模型所形成的混淆參數矩陣,Ci表示i頂點所在社區檢測模型形成的混淆參數矩陣,Cj表示j頂點所在社區檢測模型形成的混淆參數矩陣,參數Ci.(C.j)表示矩陣C中頂點數之和,參數Cij表示同時屬于不同類型社區的頂點數。CA和CB是社區劃分數量。NMI值越大,表示社區相似度越高。仍然選取文獻[19-20]中的2種重疊社區檢測算法作為對比,實驗結果如圖7所示。 圖7 3種算法的NMI測試結果對比 從圖7可以看出,隨著網絡頂點數量的增加,3種算法的社區識別精度均呈現出下降的趨勢。對于相同規模的網絡,網絡越緊密表示網絡的重疊情況越嚴重,本文算法NMI精度雖然隨著頂點數量的增加而下降,但是降低的幅度不大,即該算法的社區檢測精度和穩定性更強。 利用API網絡數據爬取工具進行真實數據集構建,數據采集平臺為新浪微博,在網絡中設定一定量的種子賬戶,獲取網絡的數據特征,具體過程為:1)選取5個相鄰的賬戶作為種子賬戶;2)基于深度搜索策略對新浪微博中的相鄰頂點進行關注主題的抓取;3)基于基準網絡對抓取過程中的參數進行調整。 通過上述數據抓取過程構建的新浪微博網絡主題為78組,頂點為900個,微博數據交互信息為5萬多條。實驗程序選取Java語言進行模型構建,對比算法仍然選取文獻[19-20]中的2種重疊社區檢測算法,算法性能的評價指標為準確率、召回率及F1值。 對于由網絡數據爬取工具獲得的新浪微博數據,其邊緣數高度依賴于數據爬取的稀疏度,文獻[19-20]算法以及本文算法對所抓取數據的檢測結果如圖8所示。 圖8 3種算法對新浪微博數據的檢測結果對比 從圖8可以看出,在低密度社區檢測情況下,3種算法的檢測結果差別不大,特別是和文獻[20]算法相比,本文算法優勢并不明顯。但是,隨著社區稀疏度的增加,社區之間的重疊和交互程度提升,本文算法因為考慮到了弱連接重疊社區的時間交互偏置影響傳播問題,所以其綜合性能上升速度較快,而文獻[19-20]算法性能變化幅度較小。上述實驗結果驗證了本文算法在社區發現上的性能優勢。 為提高弱連接重疊社區的檢測識別準確率,本文提出一種基于時間交互偏置影響傳播模型的社區檢測算法。通過設計圖分割問題的目標函數對計算資源進行均衡優化,同時構建一種影響傳播模型,以提高對弱連接用戶的識別能力,實驗結果驗證了該方法良好的社區檢測性能。下一步將對用戶交互過程中的時間間隔模型進行研究,結合影響傳播模型和時間間隔參數,以提高密集活躍社區的檢測識別性能。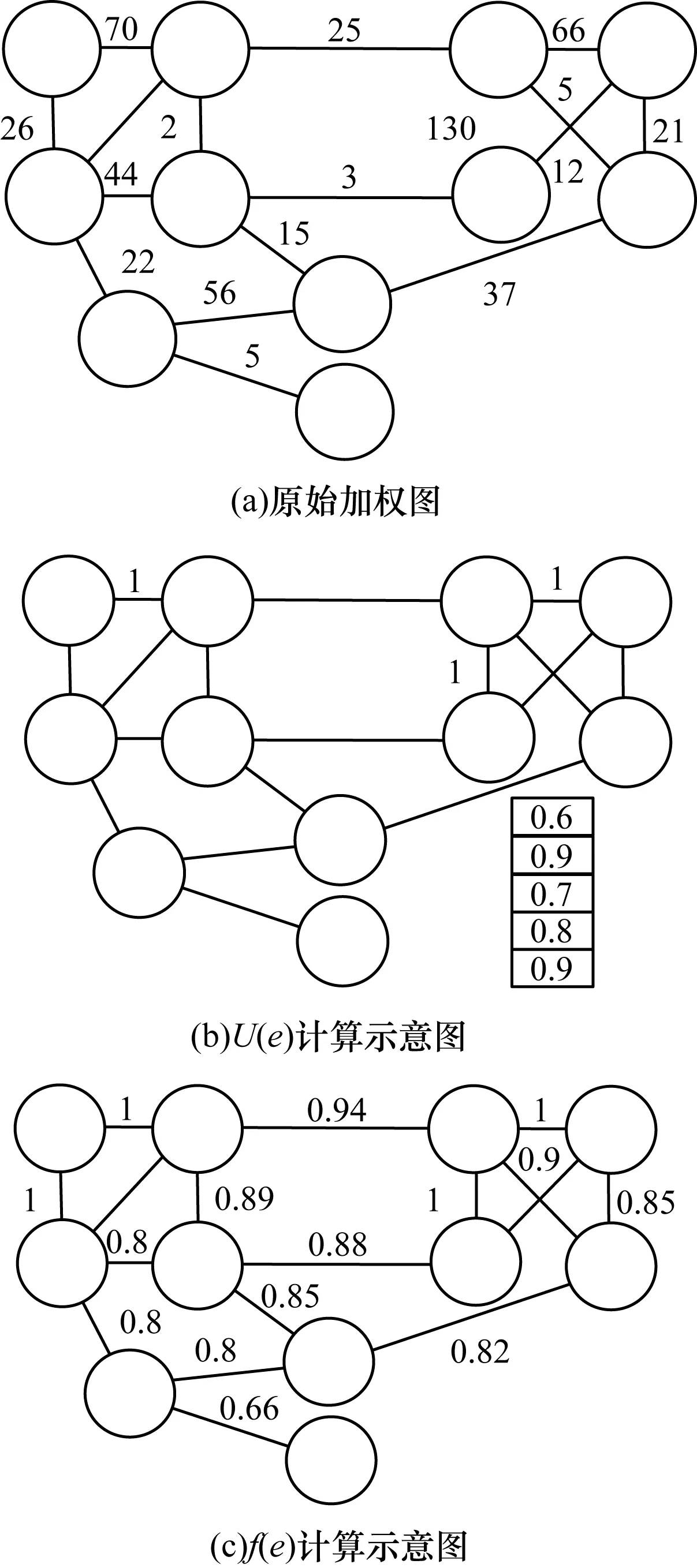
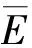
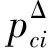
3 算法框架
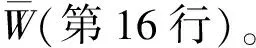
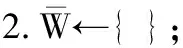

4 實驗結果與分析
4.1 實驗對象生成
4.2 穩定性對比結果
4.3 準確性對比結果
4.4 真實社區網絡檢測結果
5 結束語

