基于歸并策略的一致性時鐘同步算法

范純龍，孫強龍，劉海港

（1.沈陽航空航天大學計算機學院，沈陽 110136；2.沈陽飛機設計研究所，沈陽 110035）

0 引言

隨著系統日益龐大復雜，分布化程度越來越高，諸多領域對網絡各個節點的實時性和確定性有了更高要求。對于不同的應用場合，時鐘同步的精確度需求有所不同。在工業領域，傳感器的時鐘同步精度一般要求在ms甚至μs級別；而在航空航天領域，其大規模信息化系統所要求的時間同步精度要求在μs甚至ns級別；而在一些精密儀器高頻測試領域，時鐘同步精度達到ns級別。

本文從時鐘同步本質需求出發，在深入研究SPAD邏輯時鐘模型與MTS算法的優缺點。在時鐘擬合的過程中上引入歸并策略，優化時鐘迭代過程中的調節因子σij。仿真結果也表明改進后的MTS算法的同步精度、收斂速度、穩定性都得到了顯著提升。

1 時鐘歸并策略

在一個仿真節點群內，每個仿真節點需要測試與廣播自身與群代表時鐘延遲，以此得到一個有序的群間時鐘延遲序列T{T1，T2，T3，…，Tn}。如圖1所示，提出兩種組合策略。極大極小組合策略所產生的時鐘組合在擬合虛擬時鐘的過程中方差小，但通信代價大；而鄰近組合則是方差大，通信代價小。時鐘歸并擬合的核心是通過少量的局部信息交換實現分布式一致性。

2 時鐘擬合

2.1 時鐘擬合

假定物理時鐘是穩定的，可設計算機物理時鐘的計時模型為：

中，Ti（t）表示仿真節點i的本地時間計時結果；ai表示節點i的計時速度；bi表示仿真節點i的初始偏移量。

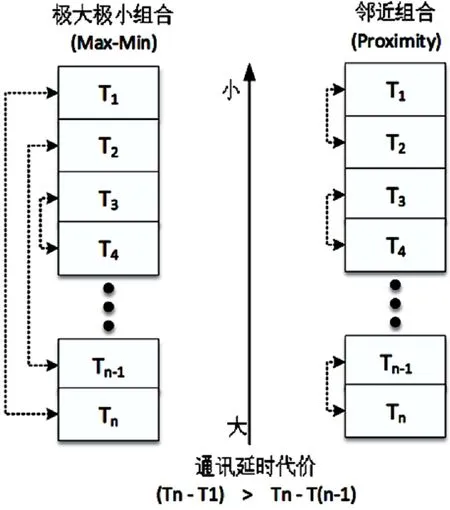
圖1 組合與歸并

圖2 時鐘擬合過程

定義擬合的邏輯時鐘的數學模型：

如圖2右邊所示，相鄰的兩個本地時鐘所擬合的邏輯時鐘模型依舊是線性的。我們期望將所有的仿真節點的本地時鐘信息，都包含至一個虛擬的線性邏輯時鐘模型中。在此，定義該時鐘為Tv（t），數學模型為：

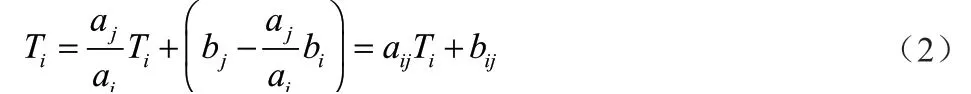
式中，av為最終虛擬時鐘頻率；bv為虛擬時鐘的初始偏移量；t為本地時鐘計數值。通過對本地時鐘進行歸并擬合，可以估算出參數av與bv。

根據式（2）以初步確定av與bv的計算方法，定義擬合時鐘的遞推計時模型：

式中，Tn表示時鐘計數值，n=1，2，3，…表示步進次數；?表示邏輯時間間隔；a表示時鐘頻率。

在時鐘同步過程中，用σijn表示節點i的n次步進時相對于節點j的校準因子，是所歸并的本地時鐘差值與上一步進差值的比值，定義：

2.2 相對頻率估計

節點i，j會在tn時刻以相同的頻率互相發送存儲各自本地時鐘計數值Ti（tn）與Tj（tn），節點i會在下一步進估算自身相對于其鄰居節點j的相對頻率，記作定義相對頻率估計的遞推公式：

式中， 表示時鐘迭代調控因子，主要作用一是降噪，二是使aij隨時間自適應性自增長。

2.3 頻率補償

每個節點都會保存自己對全局變量的估計值，并通過相鄰節點的估計值來更新自身，定義相對速率遞推公式：

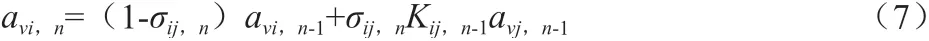
式中，avi，n-1表示節點i在n-1步進時對全局時鐘速率的估計值；avj，n-1表示參考節點j在n-1步進時對全局時鐘速率的擬合值。

2.4 偏移量補償

當所有的時鐘都完成對時鐘速率的補償，剩下的就是修復對時鐘初始偏移量的誤差，根據式（4）與式（5），定義初始偏移量的遞推公式：

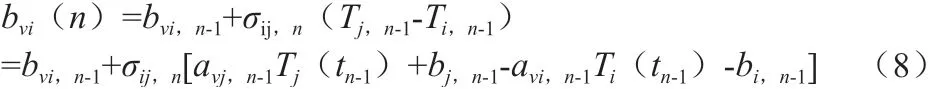
3 MTS算法

3.1 物理時鐘模型

MTS算法的核心是通過鄰近時鐘兩兩歸并，使所有仿真節點時鐘頻率快速收斂到全局虛擬時鐘頻率，以此實現全網時鐘同步。因此時鐘擬合過程的計算代價直接影響同步效果。由時鐘擬合原理可知，每個仿真節點需要保存少量參數，計算代價小，在此給出MTS算法偽代碼。

算法1 基于歸并策略的一致性時鐘同步算法

4 仿真實驗分析

實驗測試在Windows 7平臺下，基于Matlab R2018a，采用Intel core i7-3770K 3.7GHz和8GB內存配置。考慮到在實際條件下難以達到測試的絕對同步性，即很難實現全部測試節點在相同的物理時刻進行時鐘數據采樣，本文采用仿真的方式對時間同步方法進行測試與分析。本次實驗點仿真節點數量是10。仿真步長設定為0.001s，仿真步數設定為100。考慮到仿真節點的物理時鐘頻率的實際變動，確保仿真評估的可信性，選取的兩組節點的本地時鐘計時模型不盡相同，主要測試算法的收斂速度與每個節點邏輯計數值與級數均值的間隙大小。

實驗結果如下：如圖3與圖4所示，各仿真節點的大約在17步時達到全網同步，與時鐘計時均值的偏差也趨于0，算法收斂速度較快；且呈現出一旦同步，便不再失步，穩定性高。

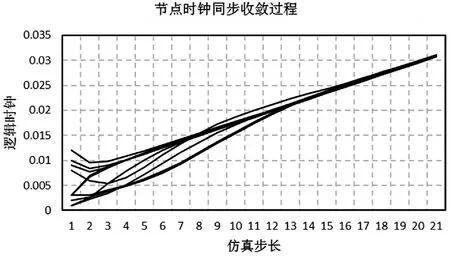
圖3 Nodes-10仿真實驗時鐘收斂過程

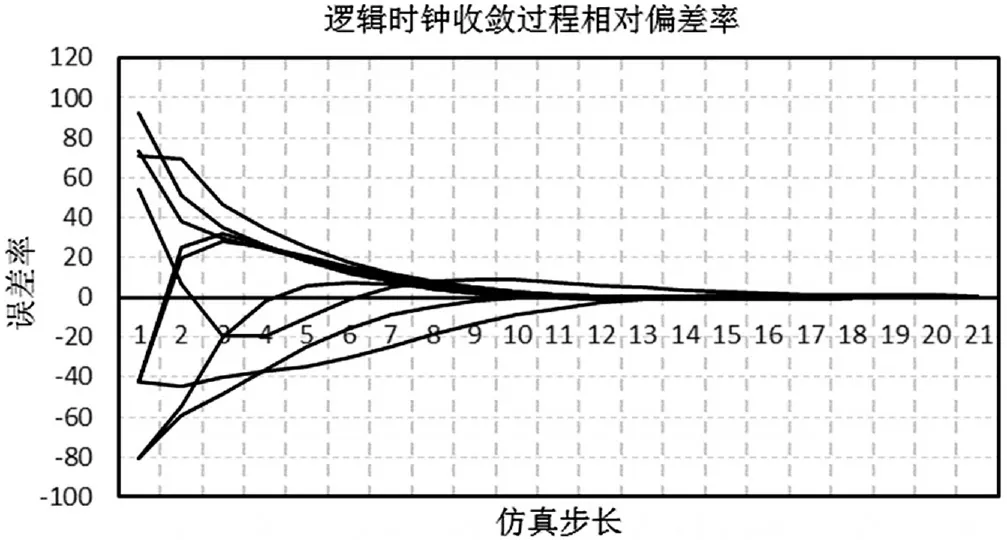
圖4 Nodes-10仿真實驗時鐘誤差率變化趨勢

在相對穩定的分布式仿真網絡中，MTS算法有著非常高的同步精度，而且其同步精度隨著時間的增長呈現正相關趨勢。在仿真實驗過程中，30步進，時鐘同步精度為10-15s，90至100步進時已經達到了10-31s同步精度。

圖5反映MTS、SPAD、ATS算法仿真節點總數量對收斂速度的影響情況。縱坐標表示達到時鐘同步所需的仿真步數，橫坐標表示仿真節點數量。分別設定五組不同數量的仿真節點N：[5，10，20，50，100]，不同仿真節點的時鐘更新速度采樣區間是[0.5，1.5]，仿真周期0.001s。采用歸并策略的MTS算法在不同仿真節點數量下，其收斂速度以及穩定度相比于ATS、SPAD都有很大的提升。

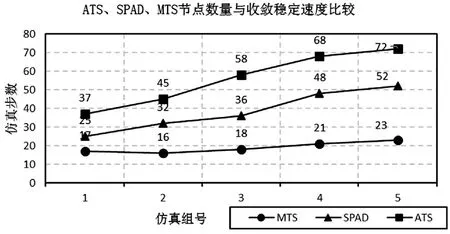
圖5 不同算法仿真節點總量對收斂速度的影響

圖6反映不同歸并策略對算法收斂速度的影響情況。仿真節點數量為20，不同仿真節點的時鐘更新速度采樣區間是[0.5，1.5]，仿真周期為0.001s。采用極大極小策略，時鐘擬合最快，算法收斂速度快，其次是鄰近策略。這兩種相比于原算法在收斂速度方面皆有提升，但需要在這里指出的是，極大極小策略會有較高的延時成本，而鄰近策略網絡延時代價較低。

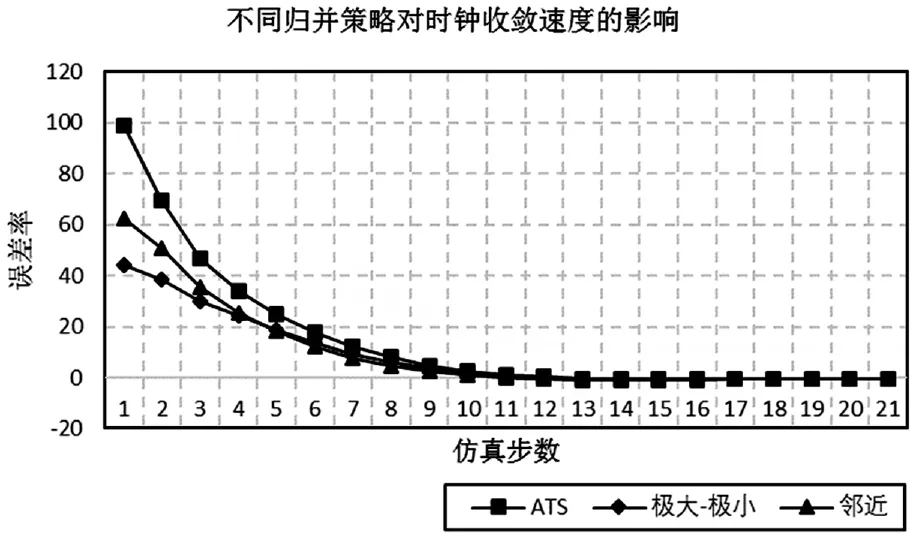
圖6 不同歸并策略下的MTS與ATS算法收斂速度影響

5 結束語

在ATS算法一致性同步的基礎上，結合SPAD算法的參量差分邏輯時鐘，并針對性地提出了一種基于歸并策略的時鐘同步算法（MTS）。MTS是一種集一致性同步、參量差分、邏輯時鐘、歸并策略等諸多方法于一體的算法。仿真實驗表明，相較于原算法，MTS在同步精度、收斂速度、穩定性方面，都有提升。同時，本文也提出了分布式節點群同步策略的設想，其準確性也有待進一步的仿真實驗驗證。