基于逆系統解耦的MSCSG姿態測量方法

于春淼，汪洲，任元，*，王衛杰，樊亞洪

（1.航天工程大學 研究生院，北京101416； 2.航天工程大學 宇航科學與技術系，北京101416；3.北京控制工程研究所，北京100190）

隨著空間航天器事業不斷發展，衛星快速發射需求越來越高，體積越來越趨近于小型化［1-2］，而姿態測量與控制一體化是航天器實現小型化的有效手段之一［3-4］。本文研究對象磁懸浮控制敏感陀螺（Magnetically Suspended Control and Sense Gyroscope，MSCSG）［5-6］是將姿態控制與姿態測量功能合二為一［7］的新概念陀螺，其具有低噪聲［8］、微振動［9］、非接觸［10］等突出優點，也是有效解決高分偵察技術所面臨甚穩超靜［11］姿態控制難題的理想選擇。MSCSG檢控一體的特點可以有效減小航天器體積、重量和功耗［12］。

在基于磁懸浮慣性器件的航天器姿態測量研究上，國內外開展了一系列研究。劉彬等［13］基于磁懸浮陀螺飛輪，提出一種將輸出控制力矩和敏感姿態角速度于一身的方案，采用洛倫茲力磁軸承（Lorentz Force Magnetic Bearing，LFMB）進行五自由度支承，其產生的磁力與電流成線性特性，從而達到測量姿態的目的，但該方案未得到實驗驗證；文獻［14］中加拿大Bristol宇航有限公司研制了一種撓性陀螺飛輪，該裝置可以在輸出三自由度的控制力矩的同時敏感航天器兩自由度的角速度，但該陀螺測量精度有待提升；房建成和任元［15］提出一種新型磁懸浮陀螺飛輪，可以對航天器同時輸出三自由度控制力矩和敏感兩自由度姿態角速度，可減小航天器姿態控制系統的體積。但是磁懸浮陀螺飛輪的轉子轉動與平動之間存在耦合，從而也導致了該陀螺測量角速度精度有限；房建成等［16］提出利用雙框架MSCMG進行姿態測量，針對測量得到的兩軸姿態角速度間存在耦合的問題，提出了動態解耦補償方法，進一步提高了陀螺的測量精度，但是該動態解耦方案在解算化簡過程中采用了高階近似，精度還有提升的空間。

此外，模糊解耦［17］、神經網絡解耦［18］、滑模解耦［19］等方法也被用于抑制兩自由度姿態控制耦合。但這些方法都需要大量的計算機資源分配，需要大量的數據進行學習，因此在航天器姿態測量系統中通常受到限制。逆系統［20］方案簡單、直觀，執行起來相對簡單，物理概念清晰，且易于理解和分析，同時對于MSCSG來說，數學模型建立較為方便，更適合采用逆系統。目前逆系統通常應用于控制，測量方面的應用還未見報道。

MSCSG是由航天工程大學2015年首次提出的一種新概念陀螺儀，并于2018年研制成功國際首臺原理樣機［5，7］。本文將在原理樣機研制的基礎上，結合控制MSCSG徑向偏轉的LFMB的工作原理建立動力學模型，推導基于MSCSG的姿態角速度測量方法，并分析MSCSG 2個測量軸之間的耦合關系，為提高航天器姿態角速度的測量精度，本文采用逆系統對其進行了解耦，在抑制2個測量軸之間耦合的同時提高MSCSG的測量精度。

1 M SCSG工作原理及動力學建模

1.1 工作原理

如圖1所示，MSCSG由上、中和下陀螺房、轉子、電機、位移傳感器、力矩器、軸向磁軸承與徑向磁軸承等部分組成。其中：轉子是MSCSG結構中的核心部件，也是MSCSG質量分布最集中的部分。電機、軸向磁軸承、徑向磁軸承與力矩器共同來控制轉子的六自由度，電機用來控制轉子轉速，即轉子軸向旋轉自由度；軸向磁軸承控制轉子穩定懸浮，即轉子的軸向平動自由度；徑向磁軸承控制轉子的徑向兩平動自由度。力矩器采用LFMB結構控制轉子徑向偏轉兩自由度。徑向磁軸承與軸向磁軸承均采用了球面結構，可保證轉子發生偏轉后的磁極面依然均勻，不至于因偏轉而產生徑向干擾力矩，從結構上消除了軸向和徑向3個平動方向對徑向2個偏轉方向的耦合。位移傳感器用于檢測轉子的位置變化信息；此外上、中、下陀螺房用于支承定子構件，同時還具有密封防護的作用。

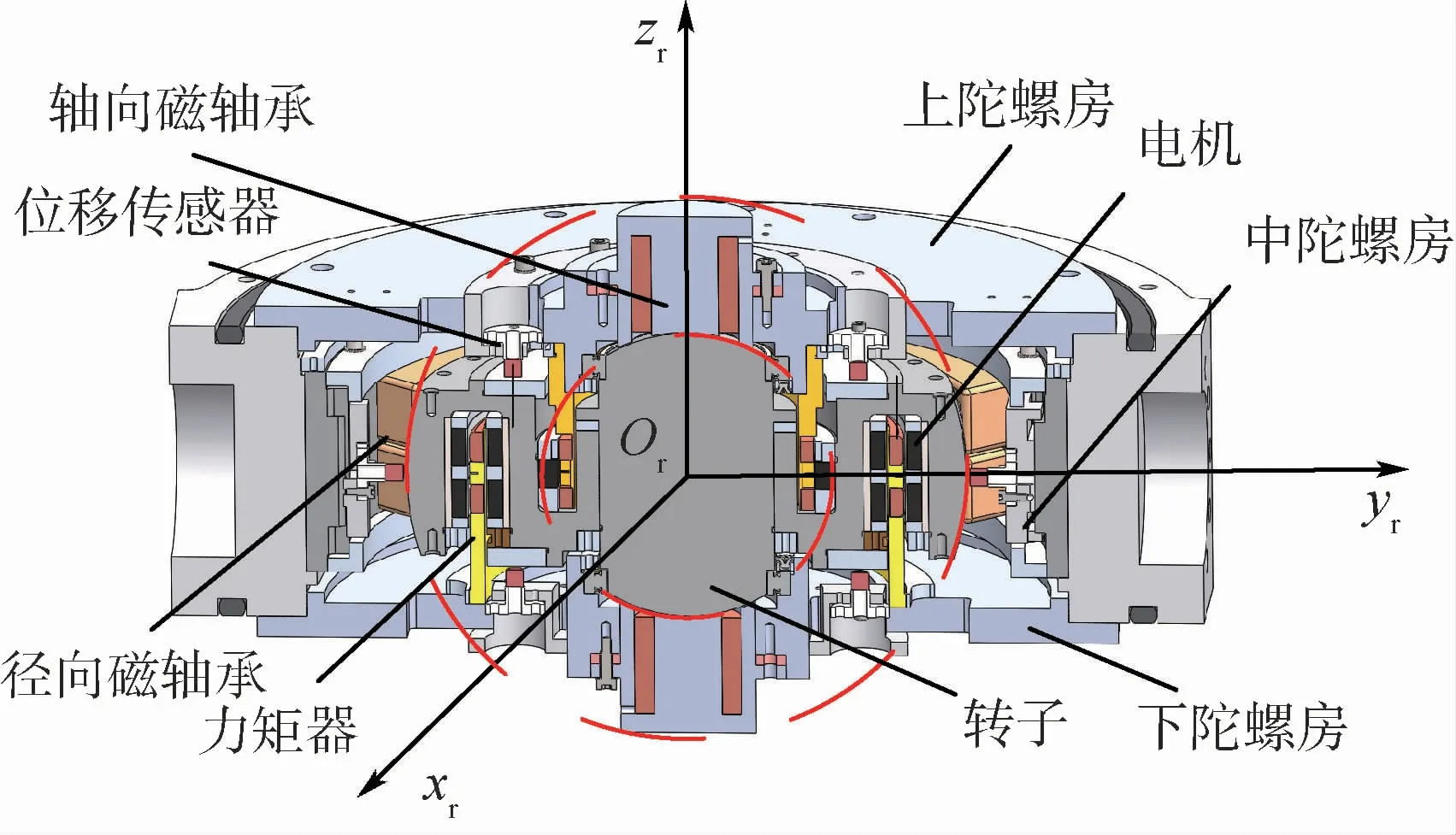
圖1 MSCSG陀螺房結構示意圖Fig.1 Schematic diagram of MSCSG gyro room structure

1.2 動力學建模

MSCSG安裝在航天器上，其定子相對慣性系具有3個轉動自由度，其轉子具有3個轉動自由度和3個平動自由度。為了便于建立MSCSG動力學模型，定義陀螺初態為計時零時時刻，高速穩定旋轉的轉子懸浮于定子腔體中心，轉子、定子球形包絡面的球心重合，定子相對于慣性空間角速度為零的狀態，同時定義坐標系如下：

慣性坐標系Oi-xiyizi：將地心赤道坐標系作為慣性坐標系，地心Oi為坐標原點，xi軸指向春分點，zi軸指向地球北極，與yi軸構成右手坐標系。

定子坐標系Os-xsyszs：定子坐標系與陀螺定子固連，原點Os位于定子球形包絡面幾何中心，取徑向磁軸承的垂直平分線作為zs軸。

轉子坐標系Or-xryrzr：與轉子固連，但不隨轉子轉動，原點Or位于轉子幾何中心，zr軸為轉子旋轉軸，當轉子位于平衡位置時，Or-xryrzr與Osxsyszs重合。

依據安培力定律，LFMB產生的電磁力表達式為

式中：f為產生的電磁力；B為磁感應強度；L為與磁場垂直方向的線圈長度；I為線圈中的偏置電流。

LFMB結構如圖2所示，α和β分別是轉子繞xr軸、yr軸偏轉的角位移，LFMB骨架中心與轉子中心重合。其與下陀螺房固連，上面安裝有上、下兩層磁鋼，為保證能夠形成閉合磁場，內、外磁鋼的充磁方向相反。同時LFMB骨架上纏繞了4組相同匝數的線圈，4組線圈保持均勻分布，每相對的2組線圈分別控制一個徑向偏轉自由度。

α和β分別為轉子繞xs、ys軸偏轉角的大小，lm為LFMB定子半徑，ls為4個位移傳感器所在圓的半徑。

當圖2中的線圈通入電流時，將產生垂直于線圈與磁場方向的安培力，上、下2個線圈的合力大小為

式中：N為LFMB中線圈匝數。

將式（2）改寫為

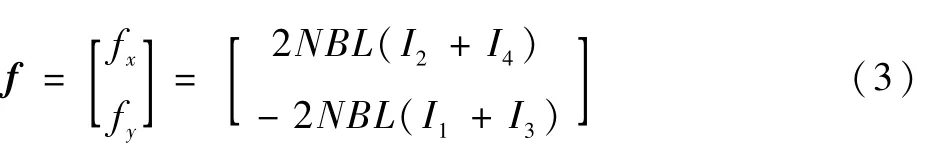
式中：I1、I3分別為xs軸正、負線圈上等大、反向的電流；I2、I4分別為ys軸正、負線圈上等大、反向的電流。則有I2＝I4＝Iα，I1＝I3＝Iβ，其中：Iα、Iβ分別表示xs軸、ys軸的偏置電流，此時相對的線圈將產生等大、反向安培力。從而有

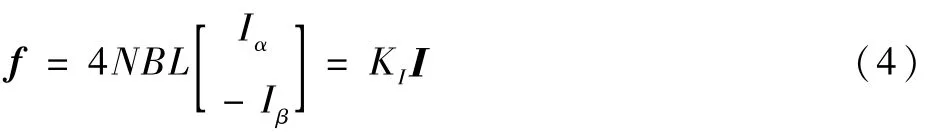
其中：KI＝4NBL為電流剛度。

由此可得LFMB提供的xs、ys方向偏轉力矩為

圖2 LFMB結構原理Fig.2 LFMB structure principle

為了獲得足夠大的角動量以增加輸出轉矩和姿態靈敏度，MSCSG設計成扁平狀。當轉子高速運行時，陀螺效應十分顯著，因此陀螺容易產生失穩。如果控制方法中沒有考慮到這一點，會導致高速轉子的失穩。控制器相位滯后，會對高速轉子穩定性產生影響。為保證MSCSG轉子控制系統的穩定性，本文采用了一種交叉反饋補償的PID控制器來解決上述問題，GPID用于分散PID控制，Gcr（s）用于交叉反饋補償，控制器設計為

Gc（s）＝GPID（s）＋Gcr（s）＝

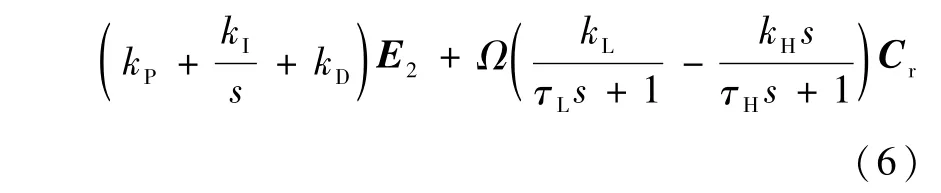
式中：kP為比例增益；kI為積分增益；kD為微分增益；kL和kH分別為低通濾波器和高通濾波器的系數；τL和τH分別為2個濾波器的時間常數；E2為2×2的單位矩陣；s為拉普拉斯算子；Ω為轉子繞zr軸旋轉的速度；Cr為交叉反饋矩陣，其表達式為

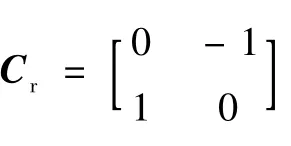
為實現電流比例反饋控制而獲得更寬的帶寬，功放系統可用一階環節建模，表示為

式中：kw為功放增益；ωw為截止頻率。

傳感器信號的反饋回路上，通過調理電路和抗混疊濾波器傳至數字控制器，表示為

式中：ks傳感器增益；ωs為抗混疊濾波器的截止頻率。

2 兩自由度姿態測量方法

MSCSG轉子控制系統由控制器、信號調理電路、電磁鐵轉子和傳感器組成，見圖3。當轉子沿軸向高速轉動時，靠軸向磁軸承產生的磁場懸浮；當發生轉動時，轉子將沿xr或yr方向產生偏轉角，高精度傳感器將檢測到轉子位置的變化，位移信號經由信號調理系統傳遞至控制器，控制器將會在xr或yr方向的線圈上施加相應控制電流，改變磁場內作用導線的電流大小并生成作用于轉子的恢復力，使轉子重新回到起始位置；最后通過測量觀察線圈上的控制電流即可推導出MSCSG的角速度。MSCSG的角速度測量主要與徑向轉動自由度有關，所以下文將通過分析轉子徑向xr和yr方向的偏轉自由度來建立動力學模型。

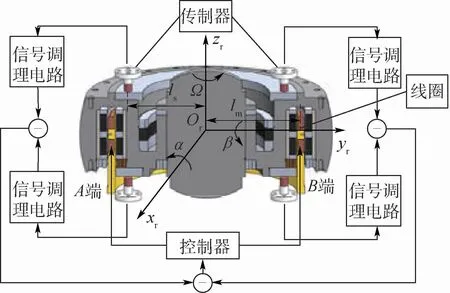
圖3 MSCSG轉子結構示意圖Fig.3 Schematic diagram of MSCSG rotor structure

根據剛體運動的動量矩定理，有

式中：Mu為轉子輸出的控制力矩；ωir為轉子的牽連角速度；Hr為轉子系下轉子的角動量，可以表示為

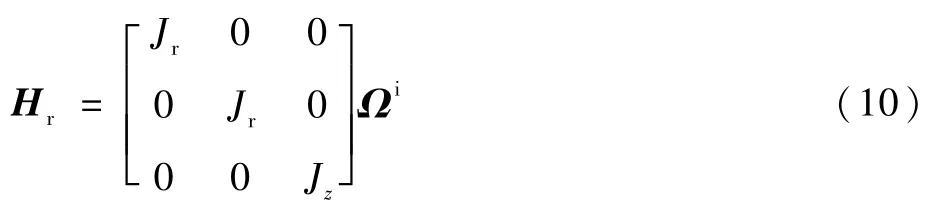
其中：Jr為轉子的徑向轉動慣量；Jz為轉子的極轉動慣量。Ωi為轉子絕對角速度，可表示為

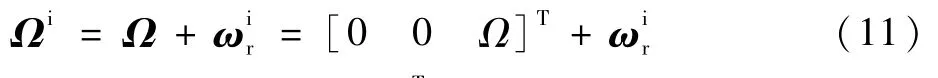
其中：Ω＝［0 0 Ω］T為轉子相對于轉子坐標系的角速度。

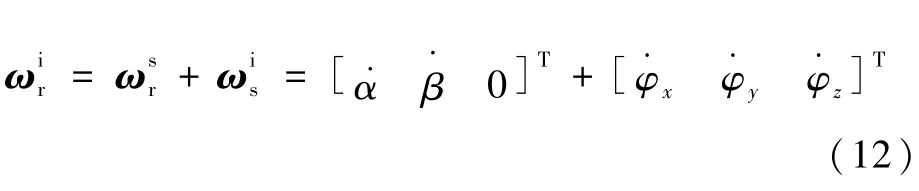
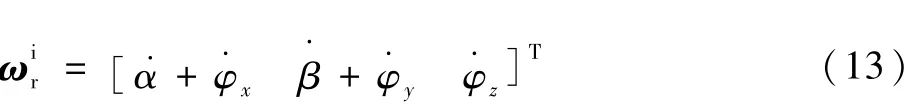
從而有

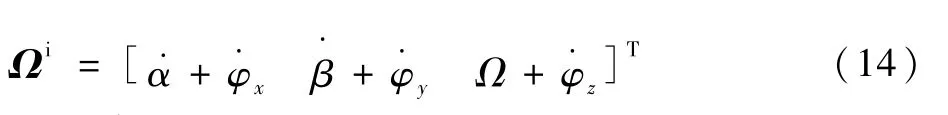
代入式（10）得

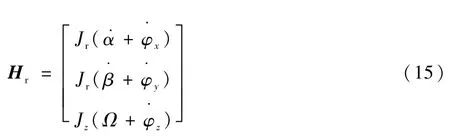
對式（15）求導得

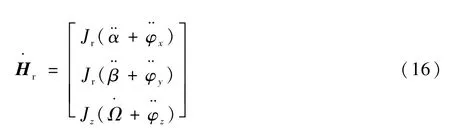
又

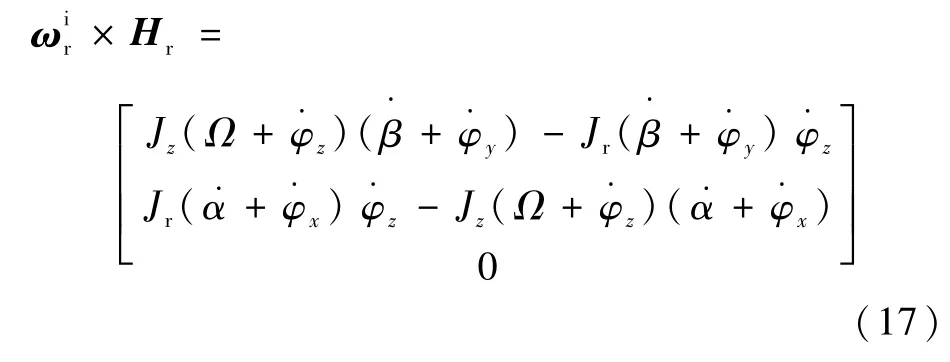
將式（16）、式（17）代入式（9）中得M u＝

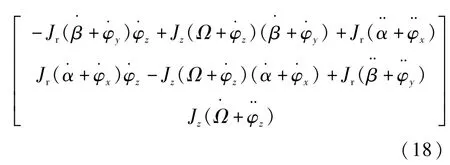
為求磁懸浮轉子所受的合外力矩，令式（18）中的φ·x，φ·y，φ·z，Ω·＝0。可得

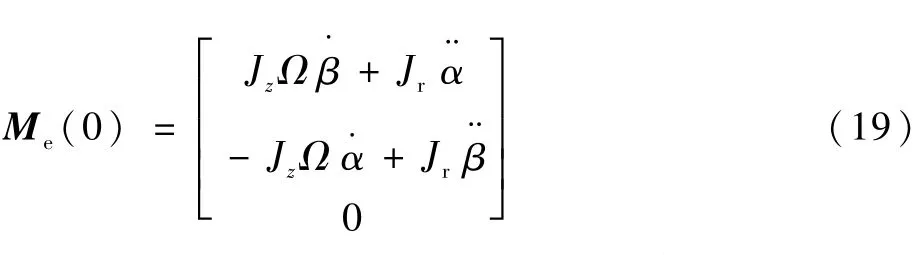
從式（18）中減去Me（0），同時假設航天器在zs軸上轉速為零，即可得陀螺轉子徑向兩軸方向上的輸出力矩為

式中：Hφ·y、Hφ·x分別為xs軸和ys軸方向上的陀螺進動力矩項，分別為xs軸和ys軸方向上的慣性力矩項。由于轉子通常運行在很高的轉速下，具有很大的角動量，而航天器的姿態角加速度很小，這樣，作為微小量，可忽略慣性力矩項，則有

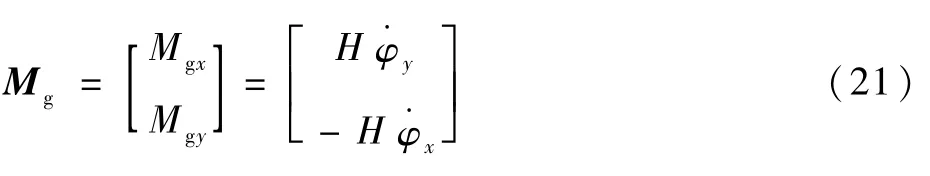
對式（21）進行拉普拉斯變換得

根據牛頓第二定律和陀螺技術方程，廣義坐標系中轉子動力學方程描述為

對式（24）進行拉普拉斯變換，可得

通過前面的一系列設計，結合每個環節的邏輯利用框圖將姿態測量原理展示出來，結果如圖4所示。

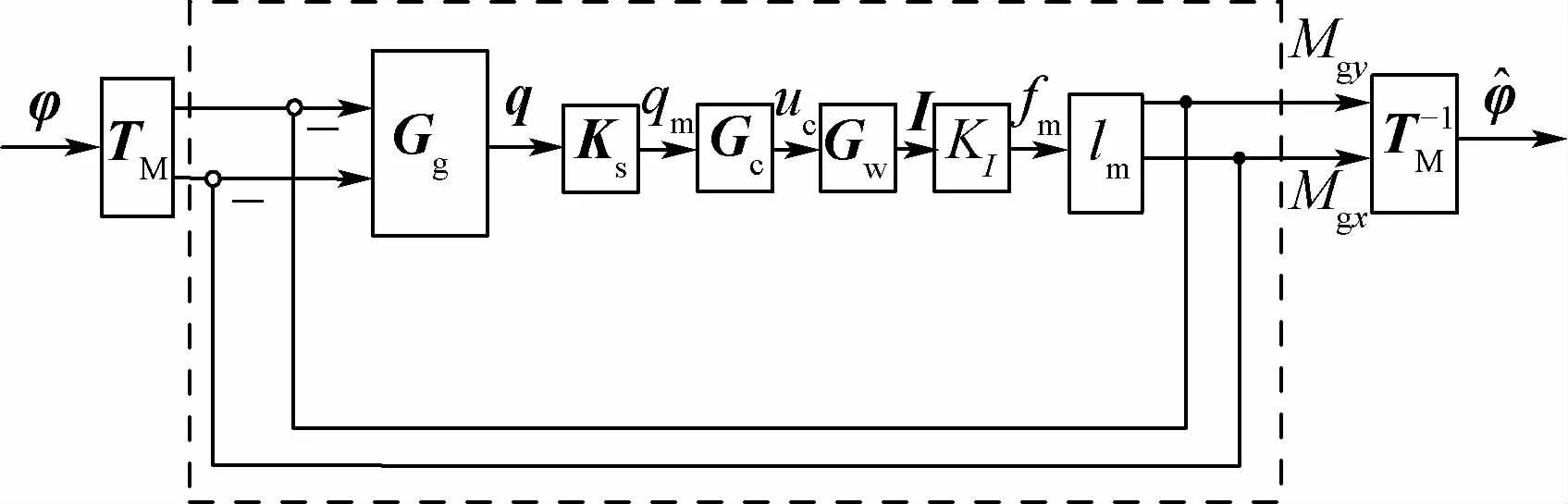
圖4 姿態測量系統原理框圖Fig.4 Principle block diagram of attitude measurement system

圖4為包含以上各個環節的姿態測量系統原理框圖，利用式（6）所設計的控制器，磁軸承控制器可很好地補償外界施加力矩，姿態角速度計算式為

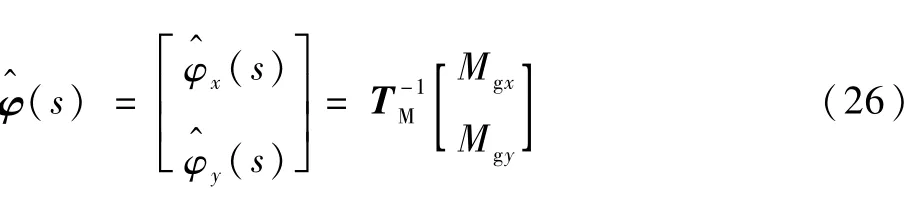
由圖4可得，從φ（s）到φ＾（s）的角速度測量傳遞函數為

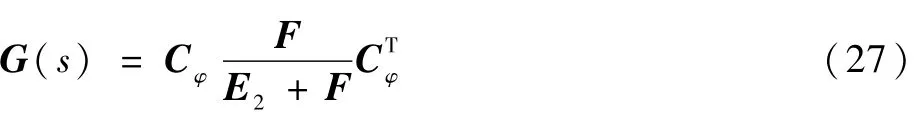
式中：F＝KsGcGwKI lmGg；Cφ為一個常數變換矩陣，其表達式為

結合式（19）、式（26）和式（27）得

式中：I＝（Iα，Iβ）為檢測得到的電流結果。代入式（28），可以由測得的電流計算得出MSCSG的兩自由度姿態信息。

3 兩自由度姿態測量解耦方法

3.1 耦合分析

聯立式（4）、式（5）和式（20）得

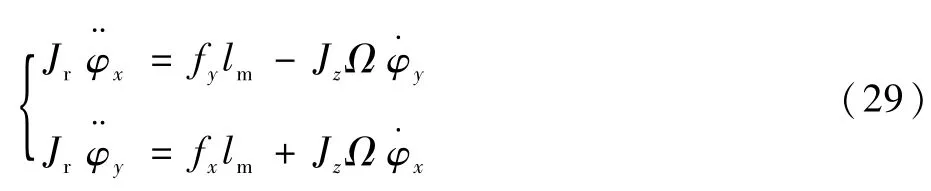
式（4）改寫為

同時還有如下關系：

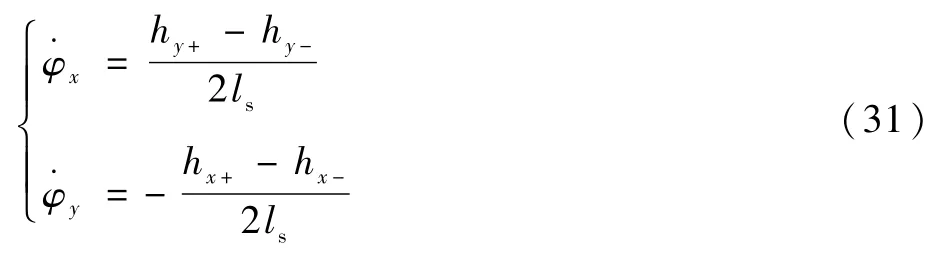
式中：hx＋、hx－、hy＋、hy－分別為xr軸和yr軸正、負方向位移傳感器的測量值，并且滿足hx＋＝－hx－＝hx與hy＋＝－hy－＝hy的關系，所以有

將式（32）代入式（29）得

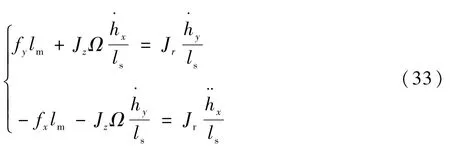
即

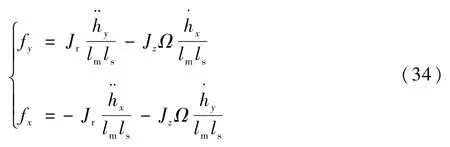
以xs軸方向為例，當Ω＝0時，fx是hx變量的函數，即xs軸與ys軸不存在耦合；當Ω≠0時，fx是hx、hy這2個變量的函數，xs軸與ys軸存在耦合。

3.2 利用逆系統對兩自由度姿態測量解耦

由于解耦的目的是弱化徑向兩偏轉自由度間的 耦 合，因此以φx、φy為輸出變量，即Y＝［y1y2］T＝［φxφy］T；同時，把Iα、Iβ當作控制變量，也就是U＝［u1u2］T＝［IαIβ］T；然后把在徑向xs軸與ys軸方向上的測量值hx、hy及他們的一階導數作為狀態變量，即X＝故 原系統Σ可寫成

式中：f（X，U）和矩陣C可以表示為

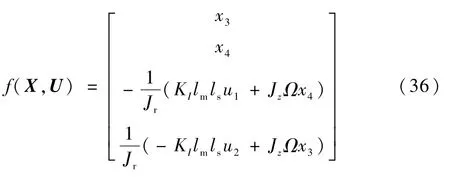
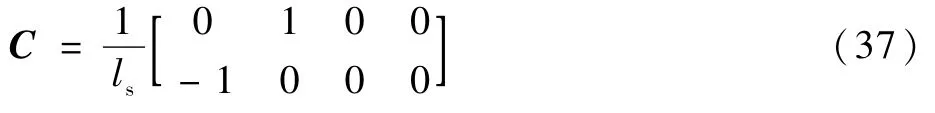
根據逆系統理論，系統輸出變量Y＝［y1y2］T＝［φxφy］T對時間進行微分，直到導數中包含控制變量U＝［u1u2］T＝［IαIβ］T為止，得

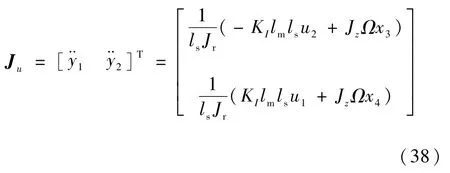
因此，雅可比矩陣D為

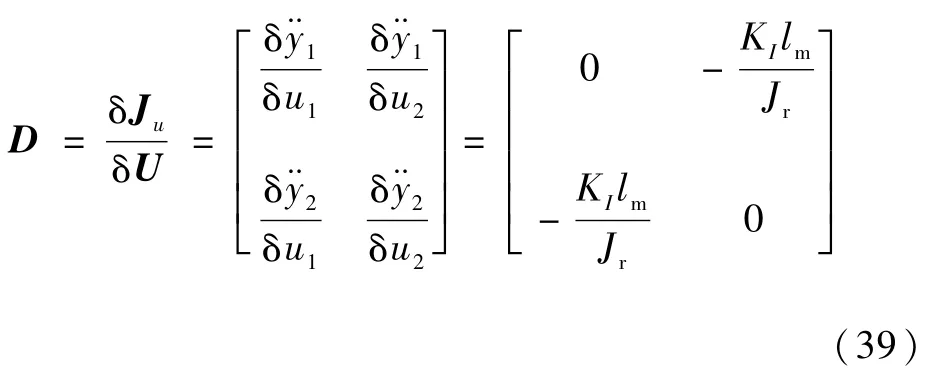
從而，通過計算可以得到

令det（D）＝0，由于電流剛度KI≠0，所以得lm＝0，但lm值恒為正數，所以det（D）≠0在系統中始終滿足。因此系統的相對順序是 α ＝［α1α2］T＝［2 2］T，滿足α1＋α2＝4≤n（n為狀態變量的數量）。因此，根據逆系統理論，可以得出原始系統的逆存在的結論，逆系統可以寫為

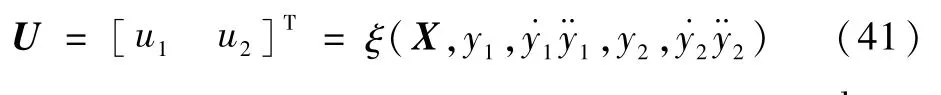
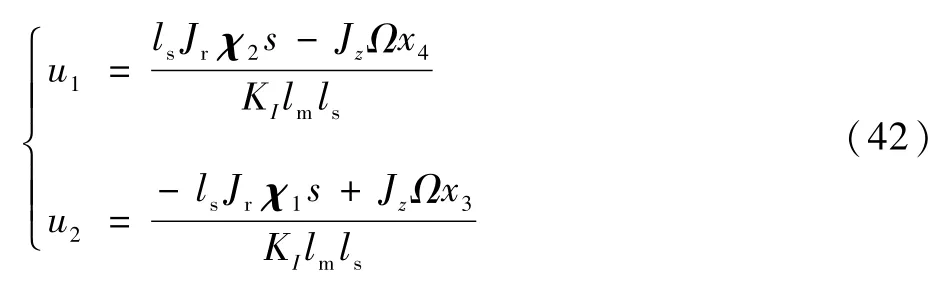
將原系統與求得的逆系統相連接，可以得到一個偽線性系統，如圖5所示。從而達到了降低徑向兩自由度偏轉之間的耦合，在一定程度上提高了航天器姿態測量的精度。

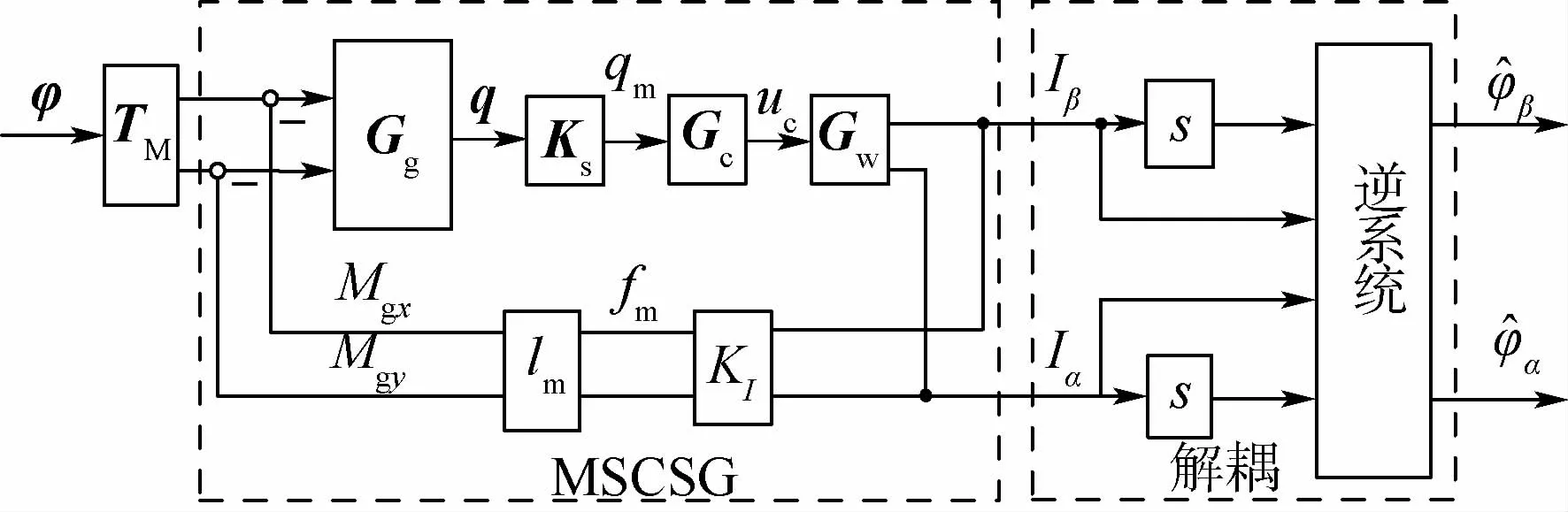
圖5 采用逆系統解耦的MSCSG原理示意圖Fig.5 Schematic diagram of MSCSG principle with inverse system decoupling

4 逆系統解耦測量仿真驗證

為了驗證本文方法在實際中的有效性和可行性，通過MATLAB中的Simulink模塊對MSCSG樣機進行建模并進行敏感解耦仿真驗證。

MSCSG樣機模型的部分仿真參數如表1所示。圖6所示是給衛星的y軸輸入振幅為1、頻率為10 Hz、20 Hz的正弦角速度信號后的仿真結果。經過仿真得知，當輸入頻率為10 Hz時，傳統方法的測量誤差為5.01%，采用逆系統解耦后的測量誤差為0.74%；當輸入頻率為20 Hz時，傳統方法的測量誤差為7.09%，采用逆系統解耦后的測量誤差為0.63%。

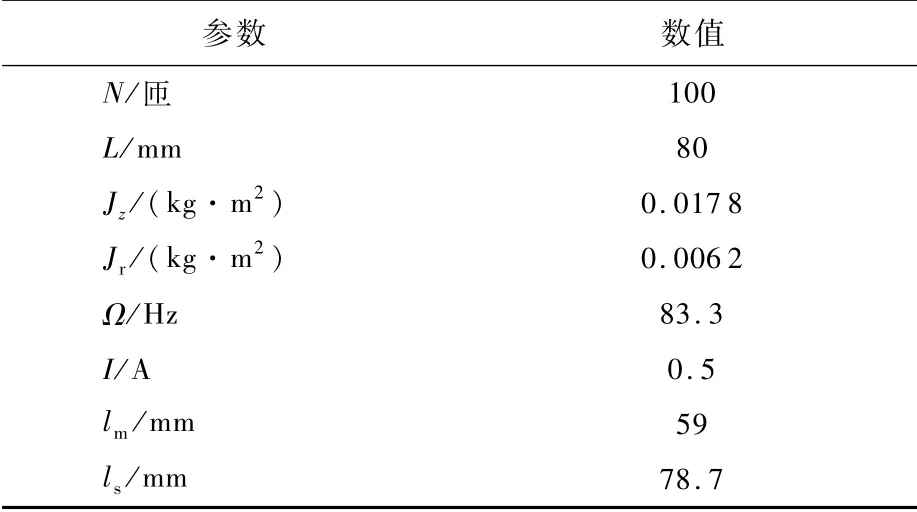
表1 M SCSG系統仿真參數Table 1 M SCSG system sim u lation parameters

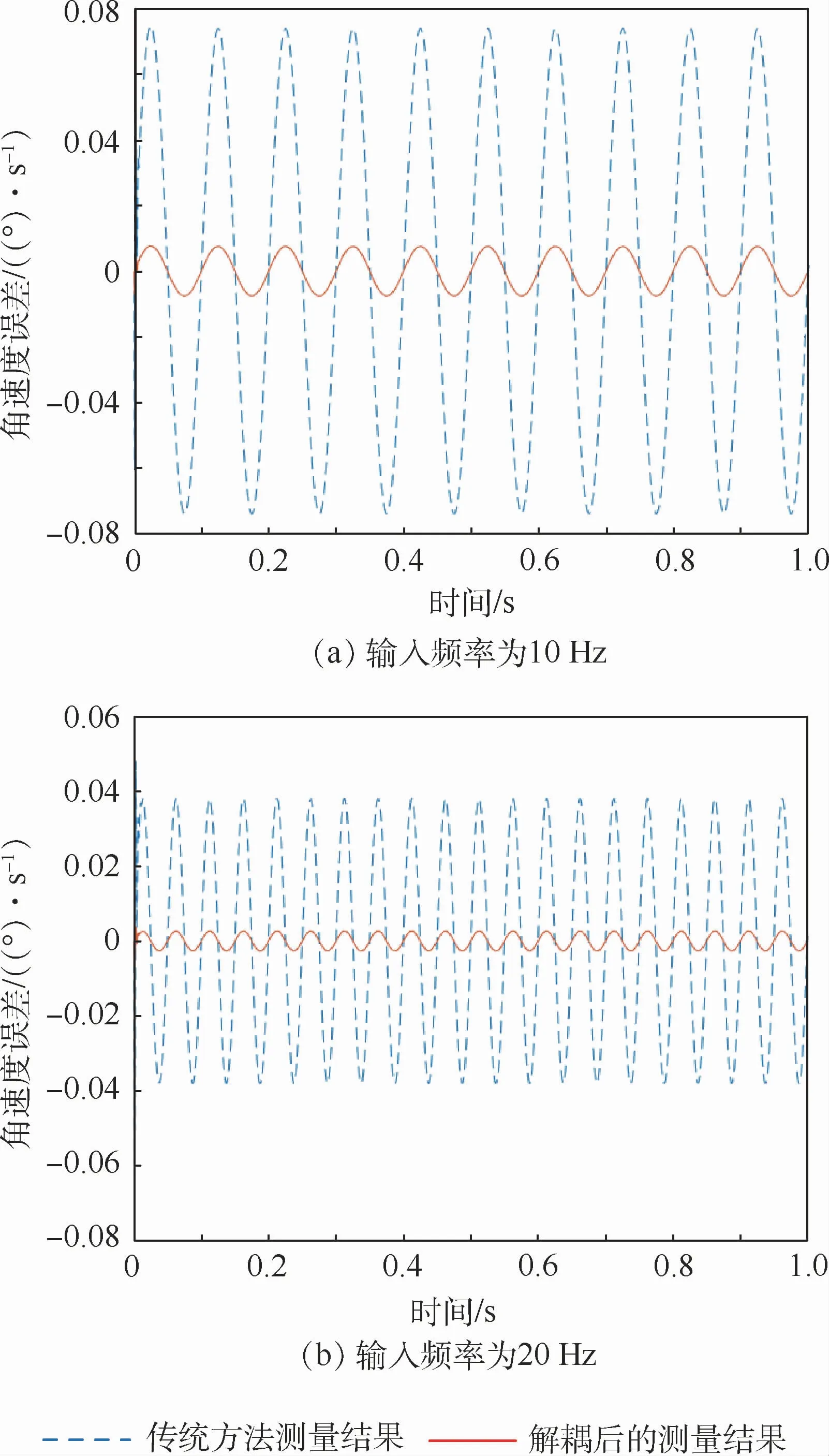
圖6 兩種方法在輸入頻率為10Hz和20Hz時的測量誤差比較曲線Fig.6 Comparison curves of measurement errors between two methods at input frequency of 10Hz and 20Hz

通過比較可知，相比于傳統方法而言，采用逆系統解耦后的測量結果更為精確，測量誤差可提升1個數量級，隨著輸入頻率的增加，本文提出的方法對提升測量精度的效果越加明顯。

為了驗證本文提出解耦方法的有效性，同樣給衛星的y軸輸入振幅為1、頻率分別為10 Hz、20Hz的正弦角速度信號，結果如圖7所示。經過仿真得知，當輸入頻率為10 Hz時，傳統方法的耦合可達4.10%，而采用逆系統解耦后的耦合可減小至0.37%；當輸入頻率為20Hz時，兩種方法的耦合分別為9.71%和0.43%。由此可見，本文提出的解耦方法相對于傳統方法具有很明顯的解耦功能，同時隨著輸入頻率的增加，解耦效果也越加明顯。

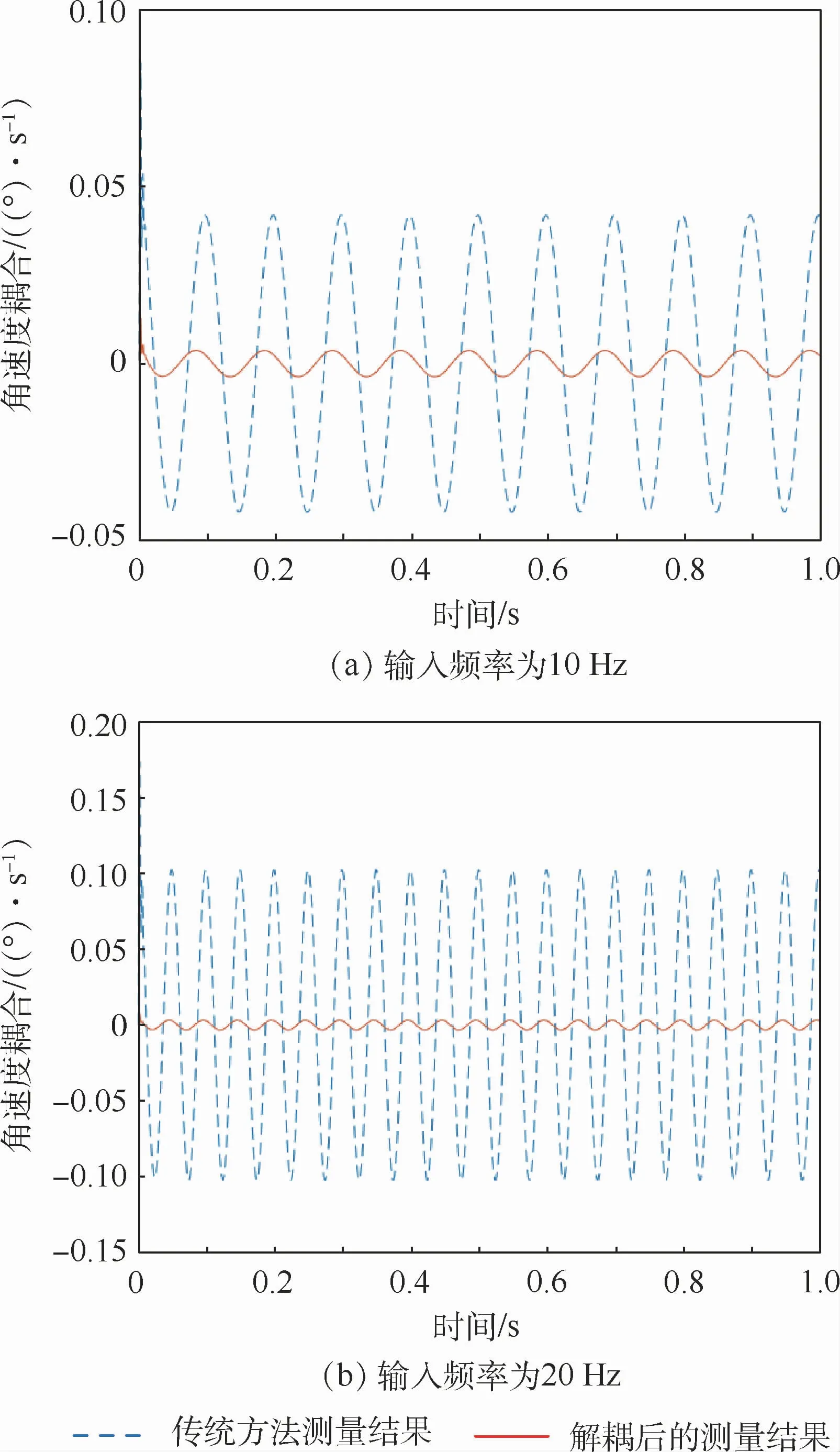
圖7 兩種方法在輸入頻率為10Hz和20Hz時的測量耦合比較曲線Fig.7 Comparison curves of measurement coupling between two methods at input frequency of 10Hz and 20Hz

5 結 論

1）傳統測量方法未采取解耦措施，直接通過忽略慣性力矩項求得航天器兩自由度姿態信息，使得MSCSG測量精度低。在給航天器輸入頻率為10 Hz和20 Hz的姿態角速度時，經過逆系統解耦測量精度可提高一個數量級。且隨著輸入頻率的增加，MSCSG測量精度越來越高。

2）采用逆系統解耦，可以很好地降低MSCSG 2個測量軸之間的耦合，在航天器y軸輸入頻率為10 Hz和20 Hz的姿態角速度時，航天器x軸的耦合可分別降低3.73%和9.28%。且輸入頻率越大，解耦效果越明顯。