基于氣動導數的類X-37B飛行器縱向穩定性分析

張慶，葉正寅

（1.西安航空學院 飛行器學院，西安710077； 2.西北工業大學 航空學院，西安710072）

隨著日益頻繁的空間應用和太空探索活動，人類對廉價、快速和可靠性高的天地往返運輸系統的應用需求日趨迫切［1-2］。比較而言，跨大氣層軌道飛行器是可重復使用天地往返運輸器中比較獨特的一種布局形式，其具有較大的氣動升阻比，強大的氣動舵面操控能力和橫向機動能力，較好的再入飛行熱、力學環境條件和可重復使用能力，能夠在火箭推力作用下跨越大氣層后在地球衛星軌道上運行，并像飛機一樣水平著陸在地面跑道上［3-5］。據公開資料顯示，截至目前，X-37B至少進行了5次太空飛行試驗，最近的一次于2017年9月9日發射升空執行“軌道試驗飛行器-5”任務，2019年10月27日返回肯尼迪航天中心，總停留時間780天，打破了之前“軌道試驗飛行器-4”任務創下的在軌停留718天的X-37B飛行時長紀錄。該飛行器在軌運行2年多，還能像普通飛機一樣在機場跑道著陸［1，5］。其設計活動可見范圍也極大，可從地面一直到外太空軌道，這也是X-37B任務的關鍵所在［5］。與飛船等傳統再入飛行器相比，這類新型再入飛行器在機動性能和可重復利用方面具有更大的優勢，已成為各航天大國研究的熱點和天地往返運輸系統的主要發展趨勢［1，6］。但是，由于這類再入飛行器氣動布局形式復雜，操縱舵面多，飛行彈道也采用升力式模式，相對于傳統的飛行器來說，出現了一系列新的氣動設計難點問題，氣動設計的復雜程度和難度都非常大［7-8］。

對于可重復使用的跨大氣層軌道飛行器來說，其巨大的性能優勢的背后是非同一般的技術復雜程度［9-12］。在空氣動力學方面，跨大氣層軌道飛行器的飛行速度范圍涵蓋亞、跨、超聲速到高超聲速，飛行高度從地面延伸到大氣層外，在如此巨大的飛行速度和高度跨越中，馬赫數效應、黏性效應、氣動加熱效應、稀薄氣體效應和真實氣體效應等復雜的因素彼此交錯，給氣動力評估和穩定性分析帶來了很大的困難和挑戰［1，8，12］。如何找到合理的氣動布局和氣動外形，使其既能夠滿足自主進場著陸、高超再入熱防護和火箭發射整流罩尺寸限制，又可以在整個飛行包線內獲得理想的氣動力、有效的操縱和滿足降落機場條件的起降性能是保障中國類似再入飛行器順利研制成功的先決條件和關鍵任務之一［1-2］。在氣動力性能預測方面，高超聲速飛行器與傳統飛行器的最大區別在于地面試驗設施無法完全再現實際的飛行環境。因此，如何預測飛行器實際飛行環境中的氣動性能參數是一項重要的工作［11-12］。目前，唯一的技術途徑是：通過風洞試驗獲得有限條件下的氣動性能參數，運用CFD計算模擬風洞環境和實際飛行器飛行環境下的氣動參數，獲得它們之間的差異，將風洞試驗數據外推到實際飛行所需的氣動參數［12］。

在氣動參數外推的過程中，存在著很多不確定性因素，如何考慮這些不確定性因素的影響是一個一直困擾著氣動工作者的難題，目前仍待攻克［10-12］。長期以來，一方面，人們努力提高風洞試驗和CFD計算的精度，降低不確定性散布；另一方面，人們也在不斷深入探索流動機理，努力摸清傳統上沒有認識到的影響因素，從而提高預測的精確程度。但是在實際飛行過程中，飛機的運動方式很復雜，會受到諸多因素（包括馬赫數、運動頻率和運動幅值等）的影響。為了考察此類飛行器隨這些因素的變化規律，本文以類似X-37B的典型跨大氣層軌道飛行器為例，對這些問題進行了探索性的研究，系統地分析了縱向氣動導數隨主要運動參數的變化規律，探討了此類飛行器氣動導數求解時的關鍵影響因素，希望能為中國未來類似軌道器的動力學分析、建模和控制律設計提供參考和指導。

1 計算方法及算例驗證

GMFlow是筆者課題組開發的柔性體動力學問題求解程序，該程序包括網格模塊、CFD模塊和應用模塊，可以計算亞聲速、跨聲速、超聲速及高超聲速等大速域范圍的流動，也可以求解從二維翼型、翼身組合體到帶增升裝置的三維全機模型等復雜外形的繞流問題，除此之外，還可以用來模擬六自由度多體分離、靜氣動彈性及動氣動彈性等耦合問題［13］。本節主要驗證程序對高超聲速強迫運動鈍錐（所選模型的頭部鈍度為dN／dB＝0.20，dN和dB分別為鈍錐頭部和尾部的直徑）的縱向動態穩定性參數的計算能力，其中非定常流場求解部分采用基于Spalart-All maras湍流模型的有限體積法，強迫運動的網格變形方法為彈簧網格變形方法。首先，用GMFlow計算了該鈍錐在馬赫數為6.85時，不同平均迎角下進行強迫俯仰運動的非定常氣動力變化情況。然后，將縱向阻尼導數提取出來，計算方法詳見第2節。最后，將計算結果與采用內伏牛頓流理論計算的結果及試驗結果［14-16］進行對比。

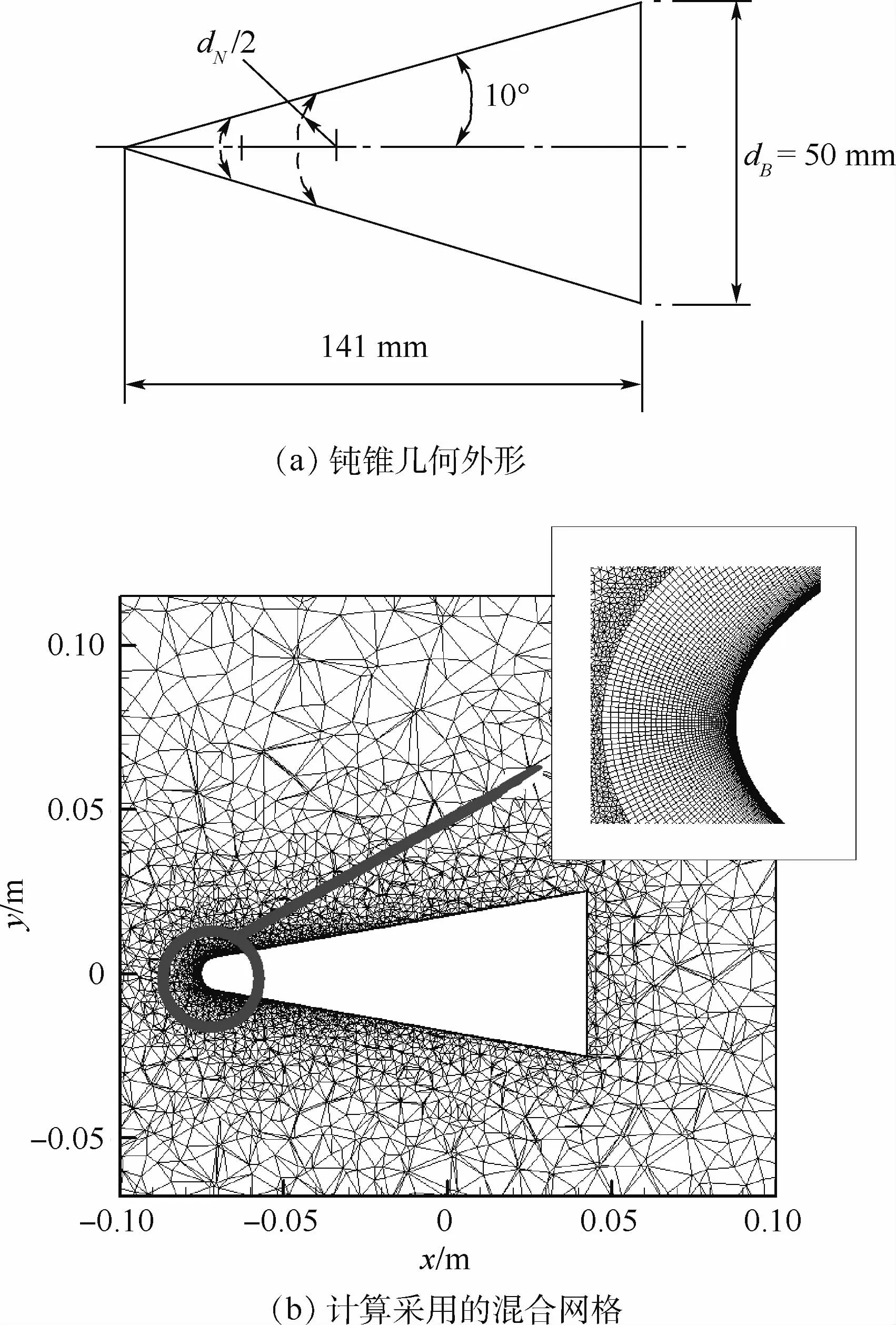
圖1 鈍錐的幾何外形和計算采用的混合網格Fig.1 Blunted cone’s geometric profile and hybrid mesh for computation

圖1（a）為10°鈍錐的幾何外形，本節所選模型的頭部鈍度為dN／dB＝0.20，重心與鈍錐頂點距離為鈍錐總長度的70%。圖1（b）為鈍錐初始時刻對稱面的網格分布情況，重心在原點處，俯仰軸為y軸。流場網格是混合網格，其中附面層是四棱柱網格，第一層高度為1.0×10－6m，一共31層，其他區域是三棱錐網格。可知，附面層網格質量保持較好，正交性也保持較好。圖2為3種方法（試驗、內伏牛頓流理論及程序求解）在不同迎角時得到的俯仰阻尼的變化情況。圖中：α為迎角，Cmq＋Cm.α為俯仰阻尼。可知，與試驗值相比，在迎角小于10°時，內伏牛頓流理論計算的數值偏大；而當迎角大于10°時，內伏牛頓流理論計算的數值偏小。程序計算值與試驗值在計算的迎角范圍內都保持了較好的一致性，由此說明了本文計算方法對于高超聲速三維構型強迫運動流場模擬的結果在一定程度上也是可靠的。

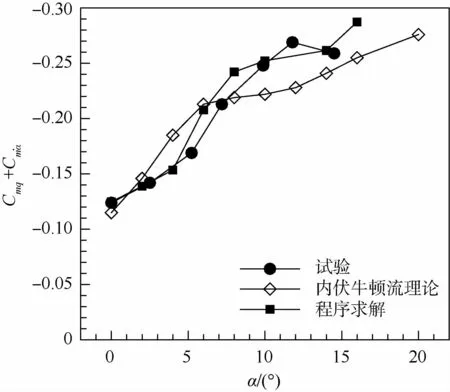
圖2 俯仰阻尼隨迎角的變化曲線Fig.2 Variation curves of damping in pitching motion with angle of attack

2 縱向氣動導數計算和分析

氣動導數是表征飛行器氣動性能的重要參數，也是高速再入飛行器動態特性分析及軌道和落點位置預測時的重要參數。準確而高效地獲取飛行器的氣動導數，特別是動態氣動導數（動導數），是飛行器設計、飛行力學和空氣動力學的重要研究內容之一［17］。為了深入認識跨大氣層軌道飛行器的動態特性，同時也為了厘清氣動導數求解時的計算參數選擇問題，本節以類X-37B的跨大氣層軌道飛行器為主要研究對象，詳細探討了平均迎角、振動幅值、飛行馬赫數及減縮頻率等運動參數對類X-37B飛行器動態性能的影響規律。

首先介紹強迫運動俯仰阻尼計算方法。與文獻［18-19］一樣，俯仰運動的運動規律可以表示為

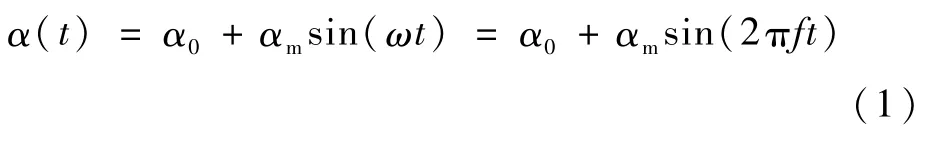
式中：α0為平衡位置處的迎角；αm為迎角的振幅；ω為簡諧振動的圓頻率；f為簡諧振動的頻率。

定義減縮頻率為

式中：C為參考長度，在本文中取平均氣動弦長；V∞為來流速度。

根據Etkin氣動力模型［20-22］，俯仰運動任一位置相對于平衡位置的非定常氣動力可以表示為ΔCj ＝Cj－Cj0＝CjαΔα＋

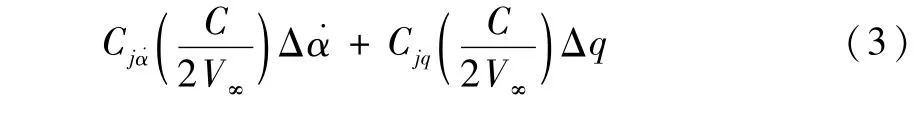
式中：Cj為任意位置的氣動力系數；Cj0為平衡位置的氣動力系數；ΔCj為任意位置氣動力系數和平衡位置氣動力系數的差值；Cjα為任意氣動力系數相對于迎角的導數；Δα和Δq分別為迎角和俯仰角速度相對于平衡位置的變化量；Cj.α和Cjq的量綱相同，都為空氣動力系數對角度隨時間一階變化率的導數。

根據強迫俯仰運動時運動規律可知

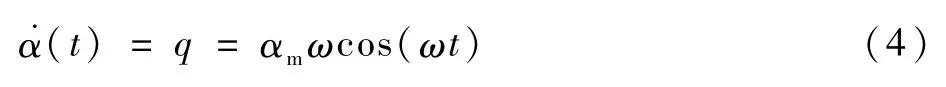
式中：q為俯仰角速度。

俯仰運動任一位置相對于平衡位置的非定常氣動力可以表示為

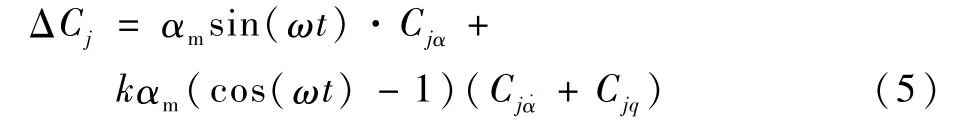
所以

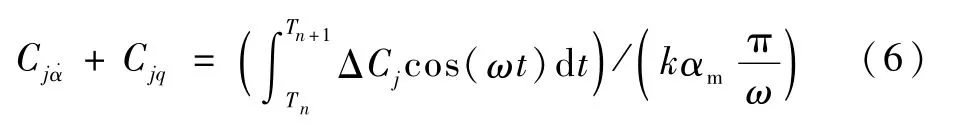
式中：Tn代表任意的時間點，Tn＋1代表對應的下一個周期。

采用強迫簡諧運動求解氣動導數的優點是計算精度高，對于不同種類的氣動導數辨識都有較好的適用性［23］，缺點是存在減縮頻率、振動幅值及振動初值的選擇問題，如果這些值選取的不合適，求解結果誤差會很大［24］。有時為了簡化分析難度，傳統意義上不考慮氣動參數的數值隨這些因素變化，但是，隨著現代飛行器對機動性和操縱性要求的提高，不得不重新考慮這些因素對氣動導數的影響規律。例如，振動幅值過小，數值仿真過程中氣動參數的增量過小，增加了隨機誤差的比例，帶來了精確預測動態氣動參數的困難，振動幅值過大，明顯增強的遲滯效應又可能造成氣動參數的快速變化，從而偏離精確值。振動頻率的選取也是如此，頻率過低，氣動增量太小，頻率過高，氣動增量過大，這些都會影響氣動導數的精確求解。為了定量分析以上因素在氣動導數，特別是動導數求解中的作用，本節以類X-37B飛行器的縱向氣動導數為例，詳細分析了飛行馬赫數、平均迎角、振動幅值及振動頻率對氣動導數計算的影響效果，計算時網格變形方法采用彈簧網格方法。

圖3（a）為所用飛行器的三視圖，該模型與美國的跨大氣層軌道飛行器X-37B類似［3-5］，主要結構由機身、機翼、斜置垂直尾翼及機身后部的體襟翼構成。全機長度為7 950mm，平均氣動弦長為2 838mm，機翼投影面積為9.86×106mm2，重心與機頭的距離為3 356 mm。圖3（b）為計算時全機不同位置的網格分布情況。可知，表面網格為三角形，空間網格為混合網格，包括附面層的三棱柱網格及其他區域的三棱錐網格。附面層第一層的高度為9.0×10－5m，增長率為1.12，一共31層。

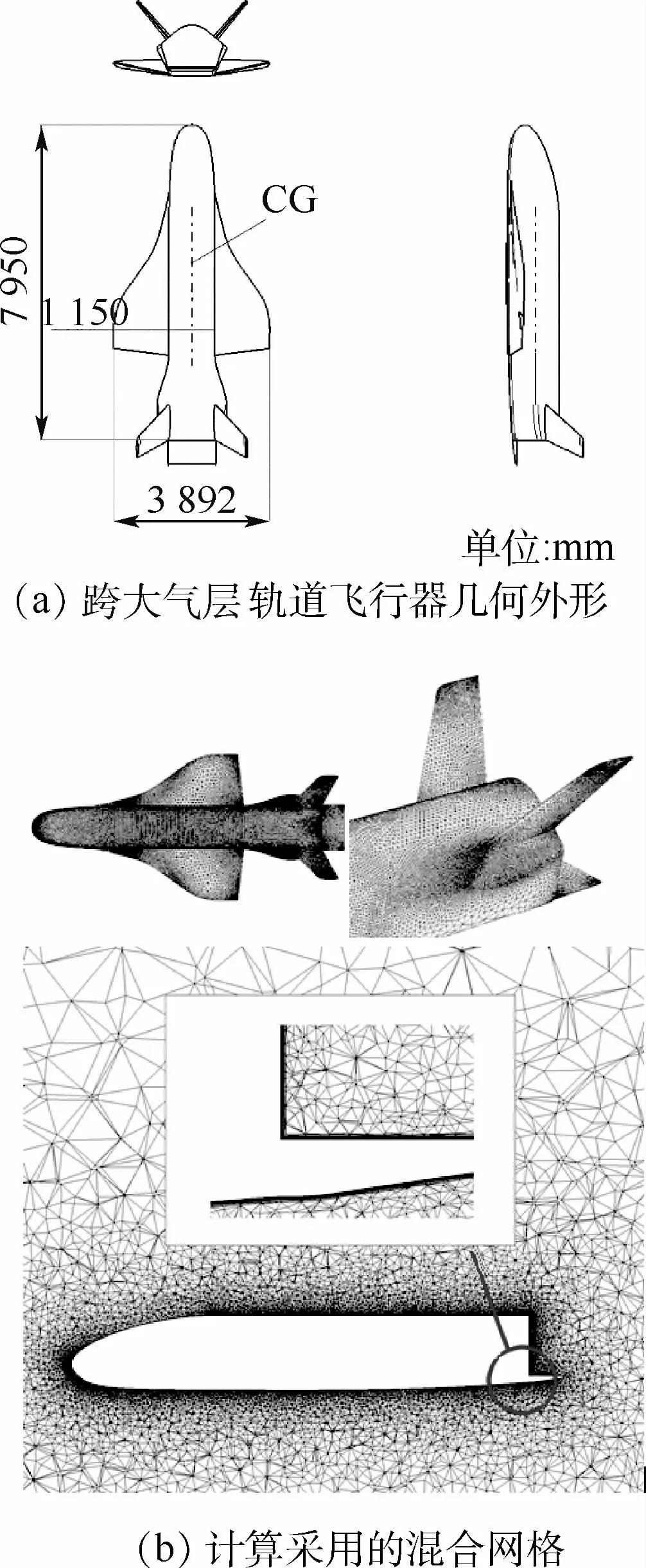
圖3 跨大氣層軌道飛行器的幾何外形和計算采用的混合網格Fig.3 Tran-atmospheric orbiter’s geometric profile and hybrid mesh for computation

2.1 平均迎角的影響

平均迎角決定了強迫運動時的平均流場形態，由于非定常氣動特性受氣流時間歷程的影響較大，為了探討平均迎角對氣動導數的影響規律，本節針對俯仰振動平均迎角對氣動導數的影響規律展開研究。

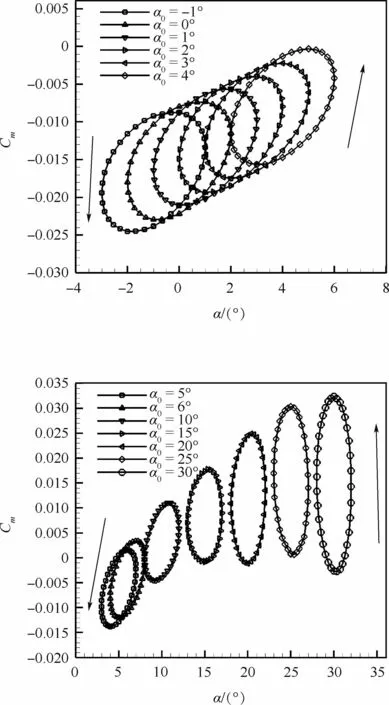
圖4 不同平均迎角時的俯仰力矩系數遲滯曲線Fig.4 Hysteresis curves of pitching moment coefficient at various average angle of attack

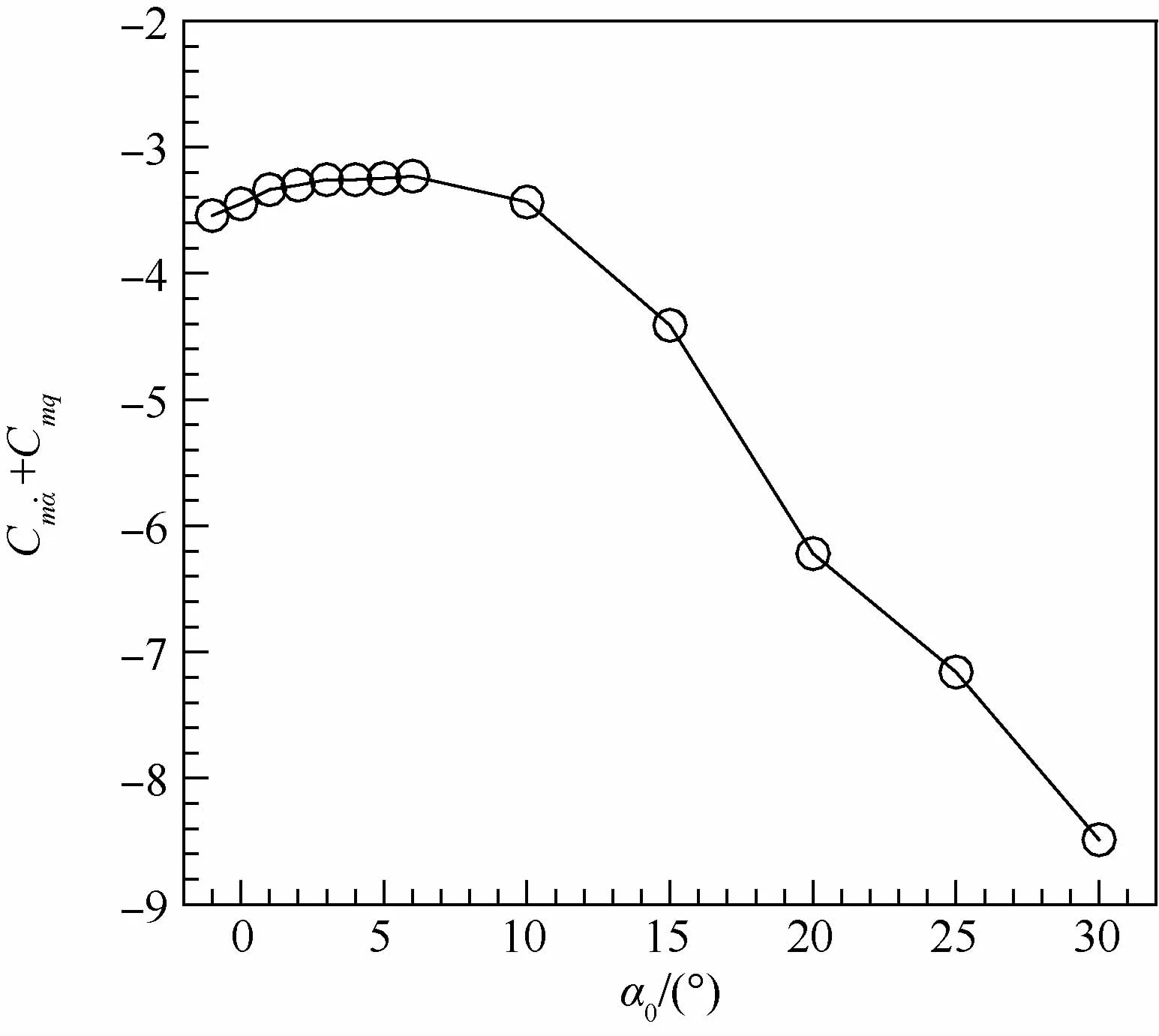
圖5 不同平均迎角時的俯仰組合氣動導數變化曲線Fig.5 Combined pitching aerodynamic derivative variation curves at various average angle of attack

圖4為強迫俯仰運動在不同平均迎角時對應的俯仰力矩系數Cm遲滯曲線，圖5為對應的俯仰組合氣動導數的變化曲線。計算條件為：飛行高度為30 km，飛行馬赫數為5.0，俯仰運動振動幅值為2°，振動頻率f＝10.0Hz，俯仰振動平均迎角α0＝－1°～30°。由圖4和圖5可知，對于不同平均迎角下的俯仰力矩遲滯曲線，所有的遲滯環都是逆時針的，說明該外形在縱向是動態穩定的。不同的是，小迎角下（－1°，0°，1°，2°，3°，4°，5°，6°）遲滯曲線的外形幾乎不變，也就意味著組合氣動導數值基本不變，當平均迎角不小于10°（即10°，15°，20°，25°，30°）后，遲滯曲線的外形越來越尖，長軸逐漸沿著逆時針方向旋轉，組合氣動導數的數值逐漸增大（見圖5），數值越大，代表動態穩定性越強。由于平均迎角越大，背風區的脫體渦越明顯，說明對類X-37B飛行器來說，脫體渦的形成增強了縱向動穩定性。實際上，其他許多飛行器也有類似情況，甚至有的飛行器在小迎角動不穩定、大迎角動穩定，從而會出現極限環運動的情況。

2.2 振動幅值的影響

就傳統上的風洞試驗來說，小振幅強迫運動是獲取氣動導數的常用手段。隨著風洞動態試驗裝備和測量設施的提高，近十幾年來，大振幅強迫運動試驗已在國內外很多風洞展開［17，23］。因為非定常氣動特性受氣流時間歷程的影響較大，所以小振幅氣動導數試驗的流動與大振幅運動達到同樣位置時的流動有很大差別。能否從大振幅振動動態試驗中獲得更多有用的氣動導數信息是最近一些研究者的研究方向，由于非定常氣動特性受氣流時間歷程的影響，為了探討強迫俯仰運動幅值對氣動導數的影響規律，本節研究俯仰振動的振動幅值對氣動導數的影響規律。

計算條件為：飛行高度為30 km，飛行馬赫數為5.0，俯仰運動平均迎角α0＝0°，振動頻率f＝10.0 Hz，俯仰運動振動幅值αm＝0.5°～30°。

圖6為不同振動幅值時的俯仰力矩系數遲滯曲線。可知，所有的遲滯環都是逆時針的，說明不論俯仰運動的振動幅度多大，該外形在縱向總是動態穩定的。不同的是，振動幅值較小時（0.5°，1.0°，1.5°，2.0°，2.5°，3°，5°），所有的遲滯環均為橢圓形，但是振幅不小于10°（即10°，20°，30°），在俯仰運動的最高和最低位置處有一個扭曲，使得遲滯曲線也同樣有一個扭曲，不再是標準的橢圓形。結合圖5可知，迎角較大時，動穩定性較強，所以，在大振幅振蕩運動到大迎角附近時，其俯仰力矩系數在上下行過程中的差異就有被拉大的趨勢，從而導致了該扭曲。結合圖7可知，雖然不同振動幅值對應的遲滯曲線外形有些許變化，但是由于在最大位置和最小位置的扭曲剛好對稱，所以所有的氣動導數數值變化不大，保持在－3.24左右，由此說明不同的振動幅值對類X-37B外形的縱向動態特性的影響不大。雖然大振幅運動的非定常效應更強，遲滯環也有明顯的扭曲，但是大振幅運動包含小振幅運動的相關信息，所以可以準確預測出非定常氣動特性。

2.3 飛行馬赫數的影響

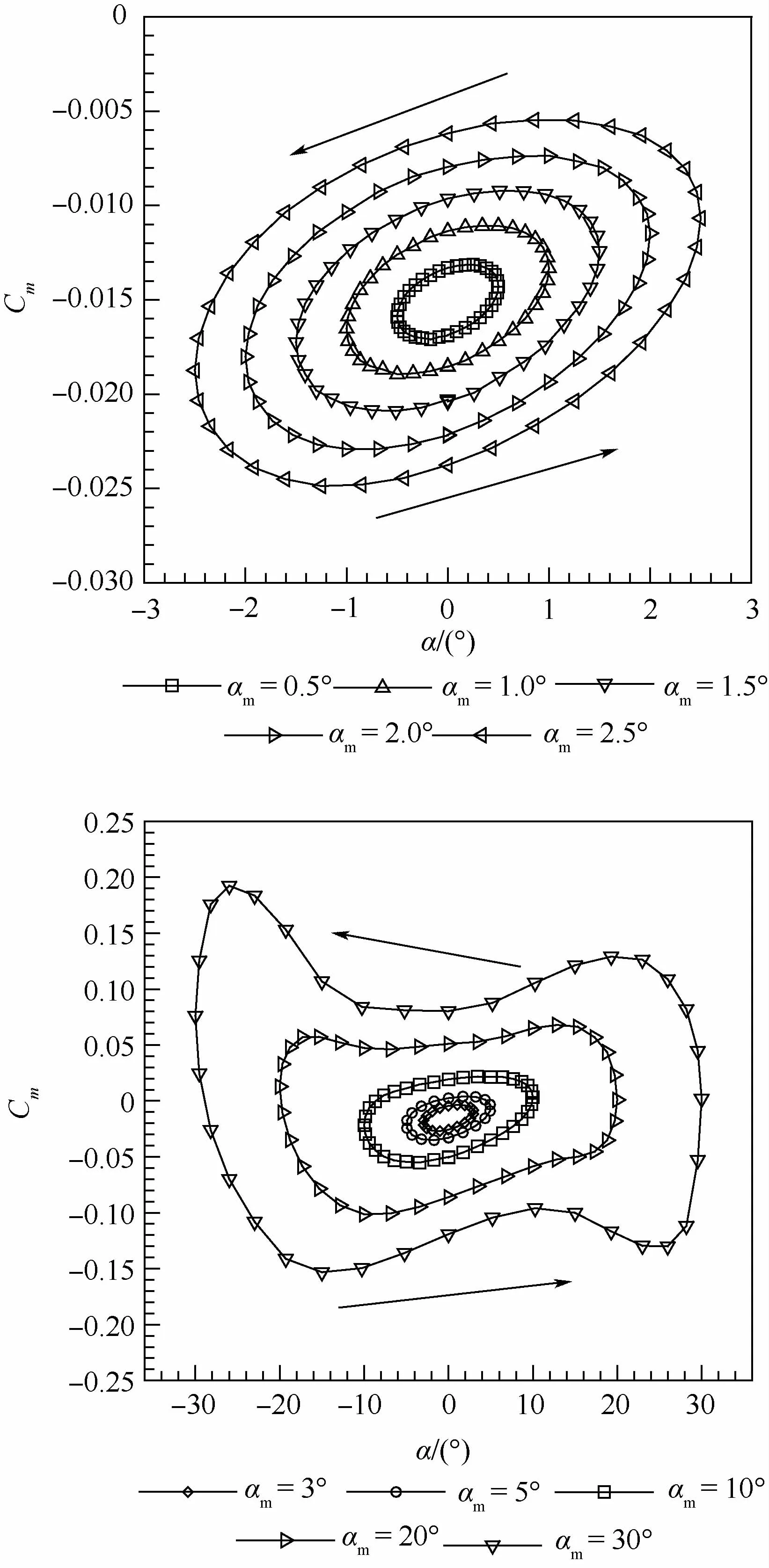
圖6 不同振動幅值時的俯仰力矩系數遲滯曲線Fig.6 Hysteresis curves of pitching moment coefficient at various oscillation amplitude

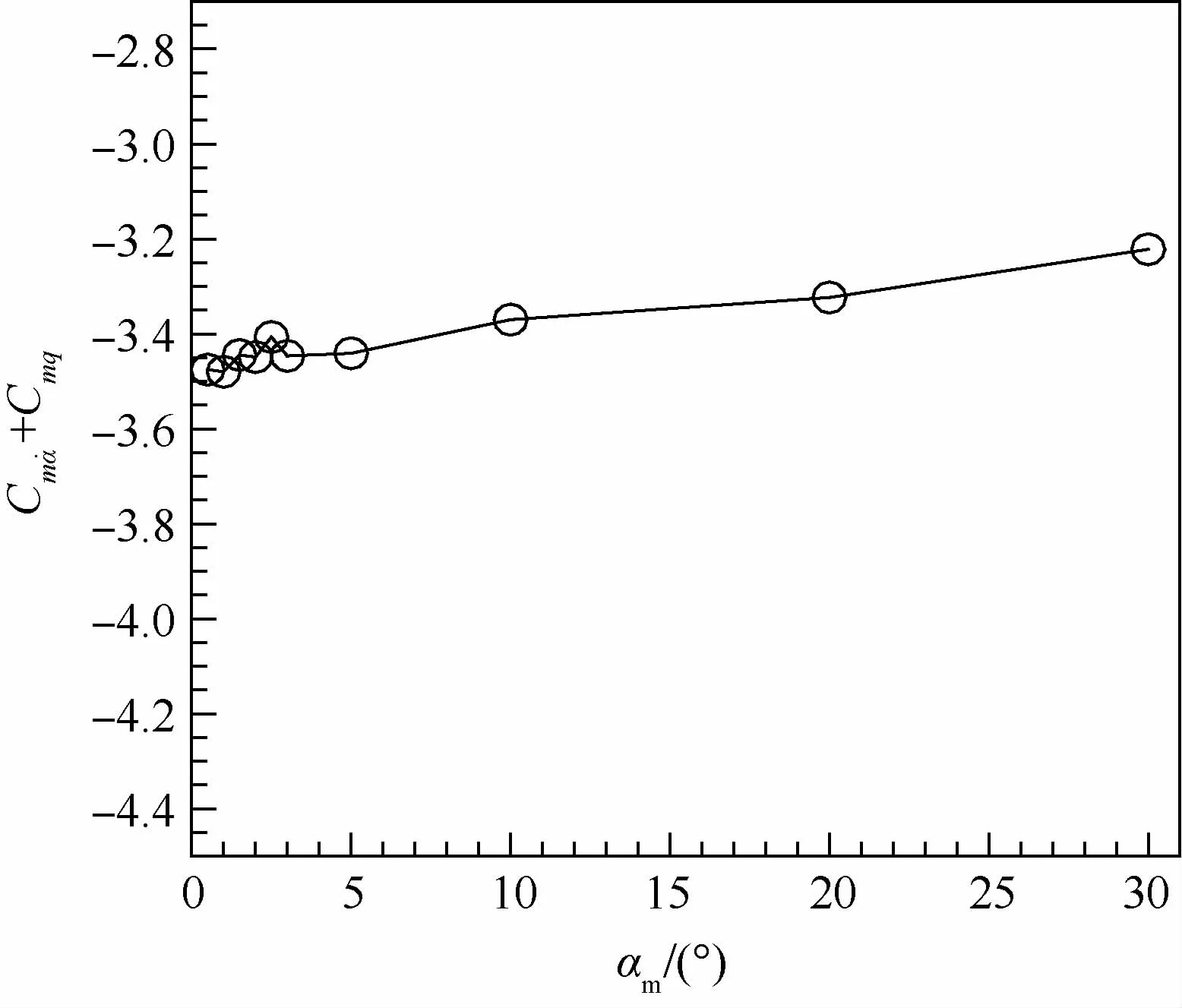
圖7 不同振動幅值時的俯仰組合氣動導數變化曲線Fig.7 Combined pitching aerodynamic derivative variation curves at various oscillation amplitude

飛行馬赫數是氣動導數的重要影響因素，飛行馬赫數的變化帶來了飛行速度的變化，從而直接影響飛行器表面的氣動力和氣動力矩，使短周期頻率增加。為了定量說明飛行馬赫數對類X-37B飛行器氣動導數的影響規律，本節計算了不同飛行馬赫數下的氣動導數。計算條件為：飛行高度為30 km，俯仰運動平均迎角α0＝0°，俯仰運動振動幅值αm＝2.0°，振動頻率f＝10.0Hz，飛行馬赫數變化范圍為0.2～15。

圖8為不同飛行馬赫數下的遲滯環。可知，不同曲線的外形雖然都是逆時針的橢圓，但是飛行馬赫數越小，遲滯環包圍的面積越大，這是因為飛行馬赫數越小，俯仰運動相對于來流來說擾動越明顯，遲滯效果也越顯著。結合圖9可知，在亞聲速范圍內，隨著飛行馬赫數增加，氣動導數數值增加，在聲速附近達到最大值，這就是跨聲速附近強烈非線性流場造成的跨聲速凹坑現象。超聲速范圍內，隨著飛行馬赫數增大，氣動導數數值減小，飛行馬赫數超過10以后，氣動導數的數值基本保持不變，這也與高超聲速飛行馬赫數無關原理相符［1-2］。

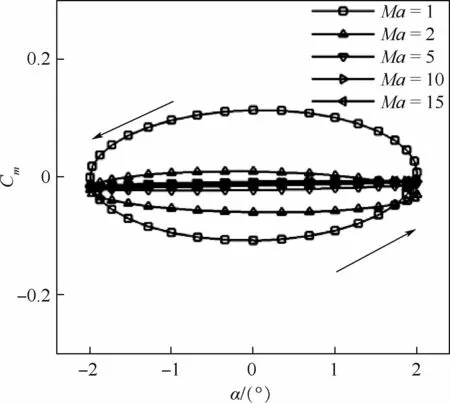
圖8 不同飛行馬赫數時的俯仰力矩系數遲滯曲線Fig.8 Hysteresis curves of pitching moment coefficient at various Mach number in flight

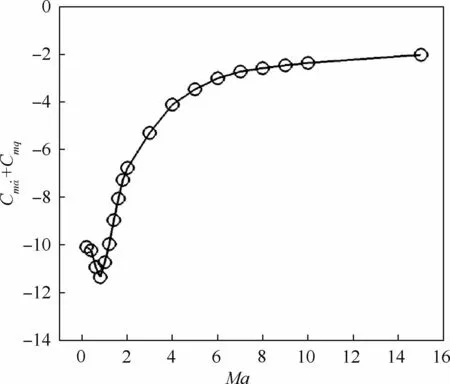
圖9 不同飛行馬赫數時的俯仰組合氣動導數變化曲線Fig.9 Combined pitching aerodynamic derivative variation curves at various Mach number in flight

2.4 振動頻率的影響

在傳統的穩定性分析和飛行仿真中，頻率的選取往往由經驗確定，很少會考慮減縮頻率對氣動導數的影響［18，24］。然而對真實飛行器的實際飛行過程而言，燃油的持續消耗和油箱的安置位置將會改變飛行器的轉動慣量；飛行高度的變化則會改變大氣的物理特性；在突風、舵偏等擾動的持續作用下，飛行器運動的固有短周期頻率會發生部分改變等，這些因素都會導致實際飛行時飛行器的固有頻率不斷地發生變化，因而氣動導數也可能發生較大的改變，這時就必須研究氣動導數隨頻率的變化關系，從而為穩定性分析、飛行仿真或是控制律設計提供更為準確的原始數據。為此，本節計算了不同振動頻率時的氣動導數。計算條件為：飛行高度為30 km，飛行馬赫數為5.0，俯仰運動平均迎角α0＝0°，俯仰運動振動幅值αm＝2.0°，振動頻率f＝0.1，1，10，50，100 Hz，相應的基于平均氣動弦長的減縮頻率為5.91×10－4，5.91×10－3，5.91×10－2，2.96×10－1，5.91×10－1。特別要注意的是，飛行器在所有的軌道上真實飛行時的振動頻率不可能到100 Hz，這里只是為了模擬某些極限的情況，探索這些極限情況下的運動特性。減縮頻率在非定常計算中是一個非常重要的參數，其實際上表征了強迫振動頻率的快慢，對氣動導數求解影響很大，減縮頻率的大小會影響氣動導數的量值乃至符號。

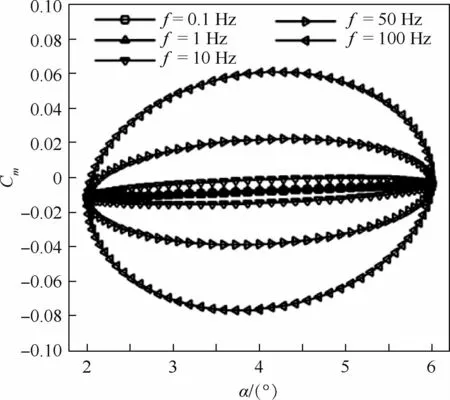
圖10 不同振動頻率時俯仰力矩系數遲滯曲線Fig.10 Hysteresis curves of pitching moment coefficient at various oscillation frequency

圖10為不同振動頻率下的遲滯曲線。可知，不同的遲滯環包圍的面積不同，頻率越高，遲滯環面積越大，但是處在俯仰運動的最低位置和最高位置處的力矩系數值保持不變。這是因為振動頻率越高，相應的減縮頻率就越大，俯仰運動非定常效應相對于來流來說擾動越明顯，遲滯效果也越顯著。而在俯仰運動的最低和最高位置，由于不同頻率運動對應的俯仰角速度均為0，所以力矩系數的數值就相同。結合圖11可知，頻率變化時組合氣動導數的數值變化不大。但考慮到類X-37B飛行器短周期頻率較低，約為0.5 Hz，計算的較高頻率的運動形式偏離了該外形的固有運動模式，預測結果可能會與真實情況不符。所以，在采用強迫運動方式分析飛行器的穩定性時，強迫運動的振蕩頻率不能隨意給定，應該結合飛行器的典型飛行狀態、典型速度分布范圍、質量分布特性和靜導數特性，估算給出典型振蕩頻率的范圍，這樣計算出的結果才有實際參考價值。

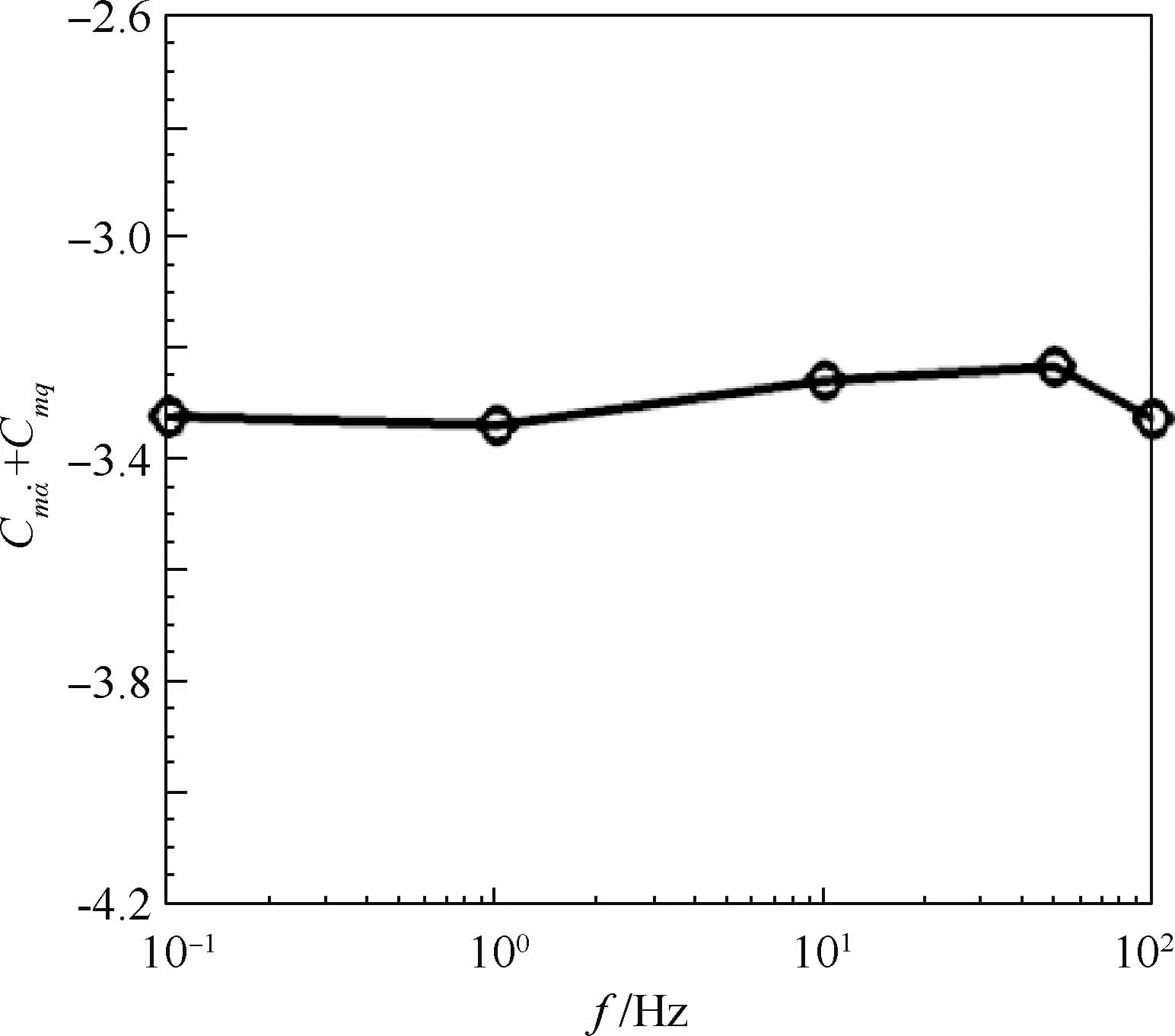
圖11 不同振動頻率時的俯仰組合氣動導數變化曲線Fig.11 Combined dynamic derivative variation curve at various oscillation frequency

3 結 論

作為一種新型天地往返輸運系統，可重復使用的跨大氣層軌道飛行器的動力學相關問題很復雜。為了定量地研究這類跨大氣層軌道飛行器在不同飛行條件下的動力學響應問題，同時也為了厘清計算參數選擇對氣動導數提取結果的影響，在Etkin氣動力模型的基礎上，本文詳細地研究了飛行馬赫數、減縮頻率、振動幅值、平均迎角等因素對飛行動態穩定特性的影響規律，結果表明：

1）對于可重復使用的類X-37B飛行器來說，在計算的平均迎角范圍內（－1°～30°），其縱向都是穩定的。在平均迎角小于10°時，穩定性隨著迎角的增加基本保持不變，但是當平均迎角不小于10°后，隨著平均迎角的繼續增大，穩定性迅速增強。

2）在計算的振動幅值范圍內（0.5°～30°），其縱向也都是穩定的，并且穩定性隨著振幅的增加有緩慢減弱的趨勢。

3）飛行馬赫數對縱向穩定性的影響比較顯著，在計算的飛行馬赫數范圍內（0.2～15），其縱向也都是穩定的。當飛行馬赫數小于1時，穩定性隨著飛行馬赫數的增加迅速增強，當飛行馬赫數繼續增大時，穩定性又開始減弱，當飛行馬赫數超過10以后，穩定性基本保持不變。

4）強迫運動的振動頻率也是影響飛行器氣動導數求解的關鍵因素，因為振動頻率與代表流動非定常程度的減縮頻率是一一對應的。本文計算的振動頻率范圍為0.1～100 Hz，對應的減縮頻率范圍為5.91×10－4～5.91×10－1。計算結果表明，對類X-37B飛行器來說，穩定性參數與強迫運動頻率的大小沒有明顯關系。但是，需要注意的是，在采用強迫運動方式分析飛行器的穩定性時，強迫運動的振蕩頻率不能隨意給定，應該結合飛行器的運動狀態、質量分布規律和靜導數特性，估算出典型振蕩頻率的范圍，這樣計算出的結果才有實際參考價值。