基于結構動力學特性的高樁碼頭橫向排架傳感器優化布置方法*

吳 俊,曹師寶,石培楊,周世良,舒岳階

(1.重慶交通大學，重慶西南水運工程科學研究所，重慶 400016;2.重慶交通大學 河海學院，重慶 400074)

隨著基礎建設的發展，我國已經建成了大量的港工建筑，這些結構在使用過程中由于碰撞、疲勞、過載、不均勻沉降等因素[1]，不可避免地會出現一些損傷，給碼頭的安全帶來隱患，事故一旦發生將會造成重大的財產損失甚至人員傷亡，因此研究碼頭結構的健康監測是非常必要的。

由于港口工程結構健康監測技術發展較晚，國內對碼頭結構健康監測系統的應用較少，目前有一些學者對國內碼頭結構進行了健康監測系統的研究。劉現鵬等[2]研究了基于光柵傳感器的高樁碼頭健康監測系統，劉向前[3]研究了大連某30萬噸級油碼頭主體結構的健康監測系統，胡皓等[4-5]研究了高樁碼頭的結構監測指標及海港碼頭健康監測系統，黃長虹等[6]針對不同形式的海港碼頭探討了海港碼頭監測的實施方法，栗鳳[7]研究了天津某高樁碼頭樁基應變監測，朱彤等[8]研究了基于光柵光纖靠船墩結構監測。這些學者針對碼頭結構健康監測系統做了認真研究，但很少有人專門針對傳感器布置進行研究，傳統的傳感器布置方法是基于工程師個人的經驗，在結構振幅較大的位置布置傳感器[9]。在碼頭健康監測系統研究中，傳感器的布置情況直接影響采集結構信息的優劣，目前針對高樁碼頭的傳感器布設的研究仍具有盲目性。

本文針對這一情況提出了基于結構動力學特性的高樁碼頭傳感器布置方案。高樁碼頭建筑物沿長度方向分成若干段，每一個分段是一個空間整體結構，由于結構分段的長度比寬度大很多，縱向剛度較小，橫向排架基本上獨立工作；又因為各橫向排架的結構形式和間距相同，其承荷條件和能力基本相同，所以選取橫向排架作為基本單元，對橫向排架進行ANSYS數值建模，提取排架結構模態信息，利用模態應變能法初步選擇動能較大的位置作為初始測點，建立初始模態置信度矩陣，然后根據序列法逐步累加測點自由度，計算每次迭代的模態置信度矩陣，直至得到感興趣的測點位置。

1 高樁碼頭結構動力學分析

高樁碼頭用系列長樁打入地基形成樁基礎，以承受上部結構傳來的荷載，上部結構為縱橫梁和樁臺樁帽等組成的整體，其實際上是一種架空式的框架結構，它的基本結構系統是橫向排架[10]，從結構力學角度分析，橫向排架屬于多自由度體系，假設其具有n個自由度，則其振動微分方程可表示為：

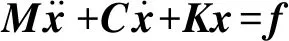
(1)

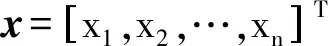
由模態疊加原理[11]，把運動微分方程通過坐標變換轉換成n個相互獨立的方程,得到其解耦形式，轉換方程如下：

x=Φq

(2)

得到其解耦形式：

(3)

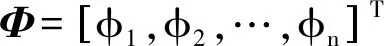
通過坐標轉換把一個n維的耦合方程式轉變為n個獨立的方程式，對于高樁碼頭結構進行模態分析可以得到結構的振動頻率、阻尼比、振型等模態參數信息。

2 高樁碼頭橫向排架傳感器布置優化

2.1 傳感器位置初選

當碼頭受到外荷載作用時，外界能量傳遞到結構上，轉換為變形能和振動機械能，結構發生振動和變形，當結構變形過大，超出材料承受極限，構件就會發生破壞。在能量傳遞過程中，能量密集處結構的振動較激烈、變形較大，模態應變能法就是依據結構的模態響應，計算每個自由度在各階振型處的動能大小，考慮結構振動時的能量分布情況，選能量較大的位置作為待測點。其計算公式如下：

(4)

式中：KEik為結構第k階模態第i個自由度對應的模態動能;Φik為模態矩陣第k階模態在第i自由度的分量；Mij為結構有限元質量矩陣的相應元素；Φjk為模態矩陣第k階模態在第j自由度的分量。

由于大型碼頭結構較為復雜，在分析模態信息時，把質量矩陣歸一化為單位矩陣，其計算公式可簡化為：

KE=diag(ΦTΦ)

(5)

式中：KE為結構的模態動能。

該方法能夠粗略計算每個自由度的動能大小，并以此作為該自由度對目標模態的貢獻度，另外對于復雜結構而言，測量得到的信號受環境影響太大，此法能突出關鍵位置，提高測量信號的信噪比。模態應變能法是粗略計算模態的動能，所以可以將其用作碼頭結構傳感器布置位置的初選。

2.2 待測點優化

根據前面的討論，由模態應變能法分析得到傳感器的初始布置測點。但是由此法得到的量測自由度存在一個弊端，即當結構受荷振動時有可能發生能量集中于某區域，只按能量分布集中布置傳感器就會造成后續重要模態信息的丟失以及傳感器的浪費；另外從結構動力學角度考慮，結構各自由度對應模態向量具有正交性，而在實際工程中，由于量測自由度遠小于結構模型的自由度，并且受到測量環境的影響，測得的模態向量已不可能保證其正交性，由此得到的模態信息陣與實際情況偏差過大。為解決這一問題，采用模態置信度準則這一工具來判定各振型向量間的相關性。Carne等[12]認為模態置信度矩陣(modal assurance criterion，簡稱MAC矩陣)是評價模態向量空間夾角的有效工具，其表達式計算如下：

(6)

式中：MACij為模態置信度系數，每一個MAC矩陣的元素值均在區間[0,1]，它反映了第i階和第j階模態向量的線性關系；Φi為模態矩陣的第i列，Φj為模態矩陣的第j列，aij為ΦTΦ矩陣的第i行和第j列元素，aii、ajj為ΦTΦ矩陣的第i行i列和第j行j列的元素。

模態置信度準則計算量測自由度組成的MAC矩陣形成的非對角元，非對角元最大值越小，表示兩模態向量夾角趨于正交，相關性越弱，越易于得到真實的模態信息。

2.3 序列法迭代優化

模態置信度準則只能判定振型向量的相關性，不能最終確定量測自由度，還需要對全局進行搜索，逐步篩選符合條件的自由度，此處基于模態置信度矩陣對全局所有自由度進行迭代試算，逐步篩選出線性獨立的振型向量和需要布置傳感器的量測自由度，其優化方法如下：

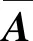
( 7 )

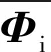
3 案例分析

3.1 數值建模

高樁碼頭結構比較復雜，取其基本結構橫向排架作為概化單元進行分析，橫向排架見圖1。

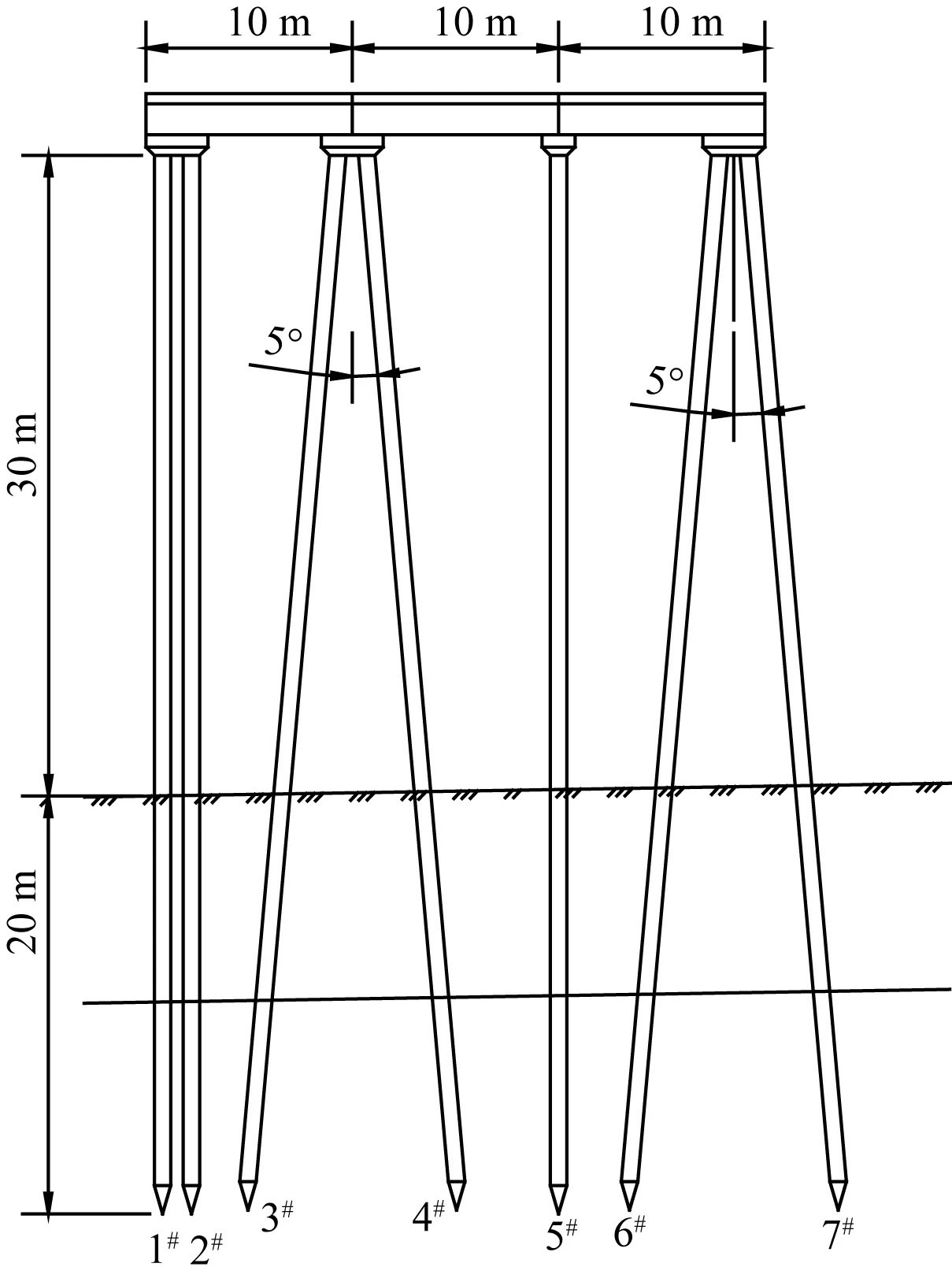
圖1 高樁碼頭橫向排架

采用ANSYS14.5軟件對橫向排架進行有限元分析，考慮碼頭中間部分橫向排架受兩側縱梁約束，縱向不發生變形和振動，所以選取平面梁單元建立有限元模型。排架的橫梁和樁均選BEAM3作為單元類型，橫向排架橫梁長10 m、樁長50 m，土體以上的樁長為30 m，樁底端采用固結形式。縱橫梁為混凝土T型梁，其尺寸見圖2。樁基為鋼管混凝土摩擦樁，樁身直徑1.2 m，鋼筋混凝土材料楊氏模量為21 GPa，泊松比取0.2，密度為2 500 kg/m3。樁土作用采用土彈簧模型，上層土體為粉砂質黏土，土體抗力系數M1取2 500 kN/m4,下層土體為粗砂質黏土，土體抗力系數M2取6 000 kN/m4。用ANSYS建成的有限元模型見圖3，該模型共有526個節點、525個單元。

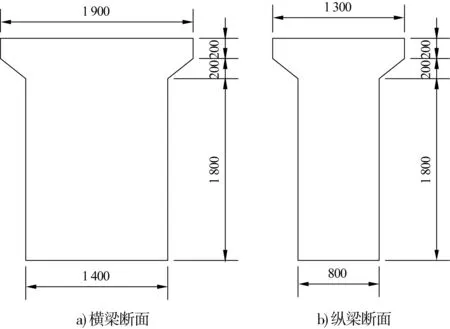
圖2 縱梁和橫梁斷面(單位： mm)

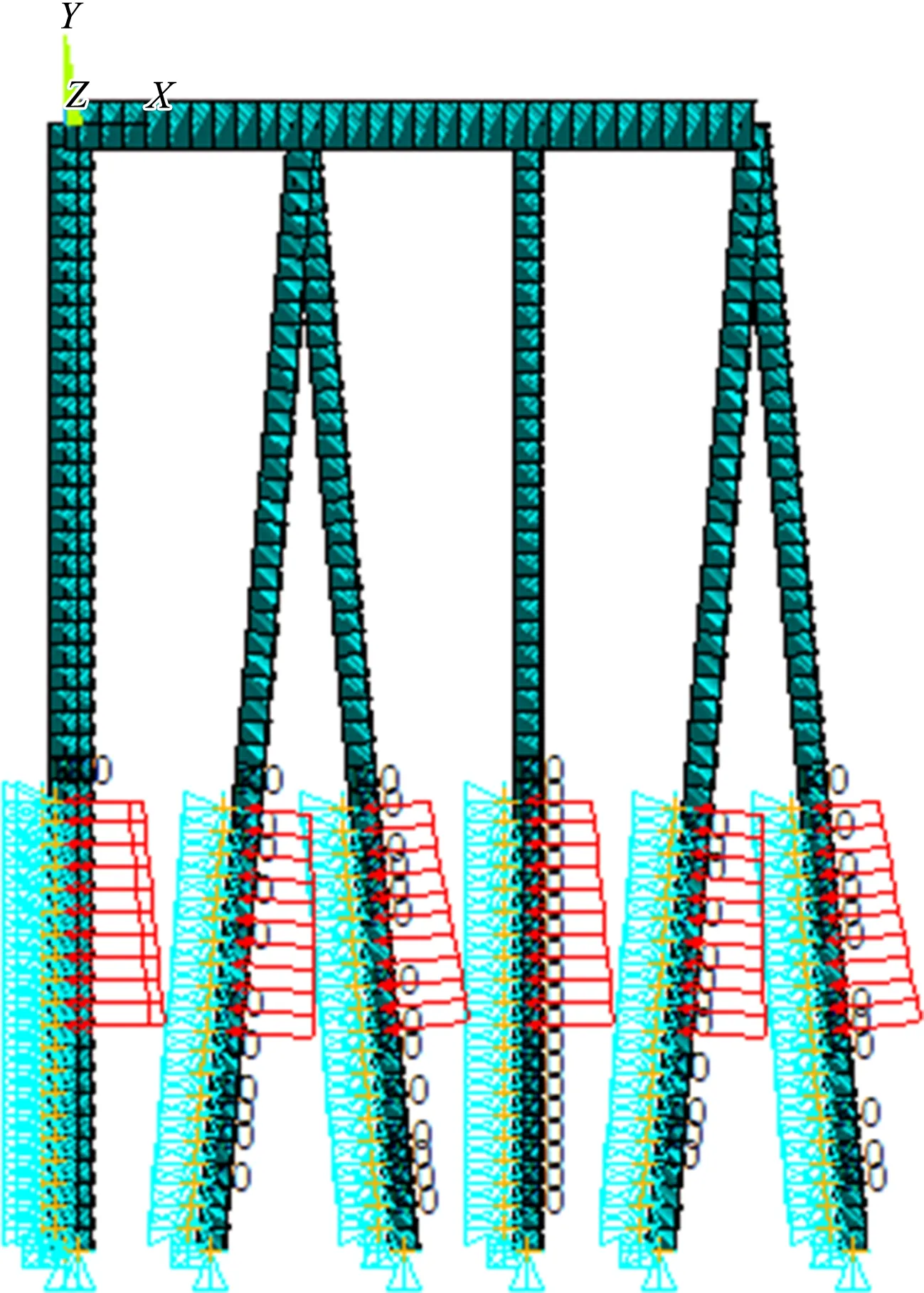
圖3 橫向排架有限元模型

模態提取方法采用Block Lanzcos法，前8階頻率見表1。對應的前4階振型見圖4。

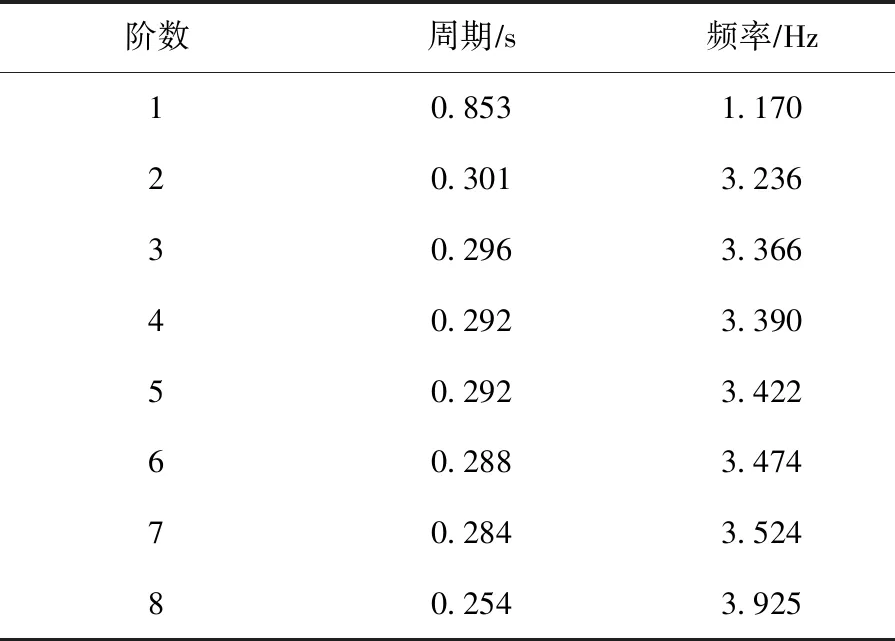
表1 有限元模型模態分析的周期和頻率

圖4 排架前4階振型

3.2 傳感器布置及優化

在圖4所示的振型中，觀察到各單元在豎向的模態均為零或接近于零，故此處僅考慮橫向的模態。

3.2.1傳感器初始布置

摩擦樁土體以下不布置傳感器，只考慮土體以上樁和梁，根據模態應變能法，由式(5)計算得到有限元模型所有節點在橫向的動能，選擇貢獻度比較大的節點作為初始選擇的測點，選出3個點作為初始測點，分別為49、99、251，由其計算的初始自由度MAC值見圖5。

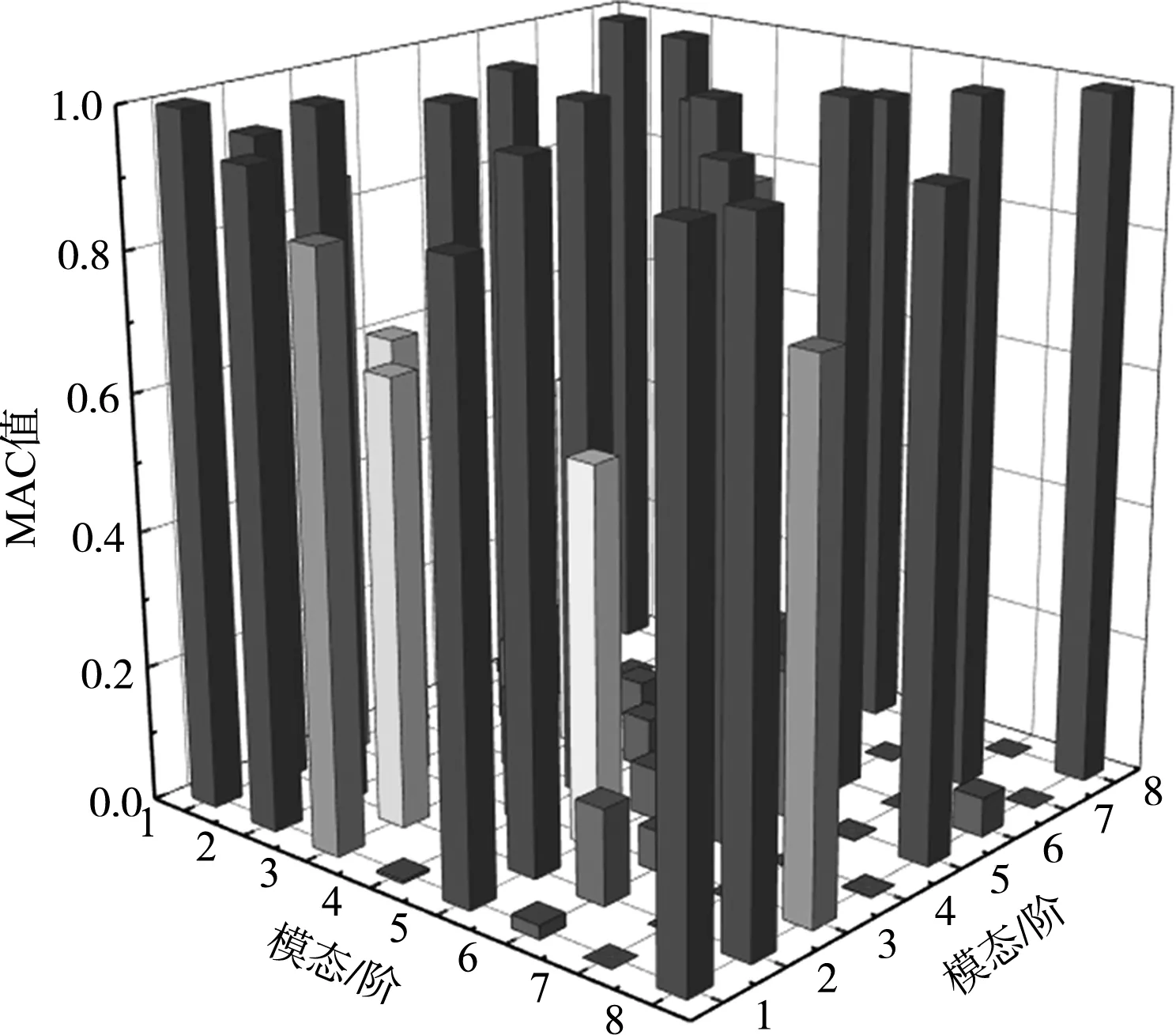
圖5 初始自由度的MAC值

由于MAC矩陣為對稱矩陣，可以看出MAC非對角元中均比較大，需要優化測點位置以減小MAC非對角元值。

3.2.2序列法迭代優化

在MATLAB中利用式(7)迭代計算MAC矩陣，MAC矩陣中非對角元最大值的選取應該根據試驗對象以及設備精度而確定，此處研究其每次迭代的優化曲線，取其前50個增加的自由度，其收斂曲線見圖6。

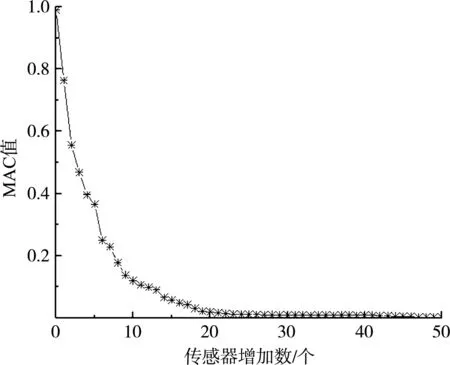
圖6 MAC非對角元變化曲線

3.2.3優化結果

隨著傳感器數量的增多，曲線呈下降收斂趨勢，當在新增加的第9個自由度時，曲線變化已經較緩，此時所對應的測點為傳感器布置所選的測點，迭代計算得到最終的測點為12個測點，其分布見圖7。

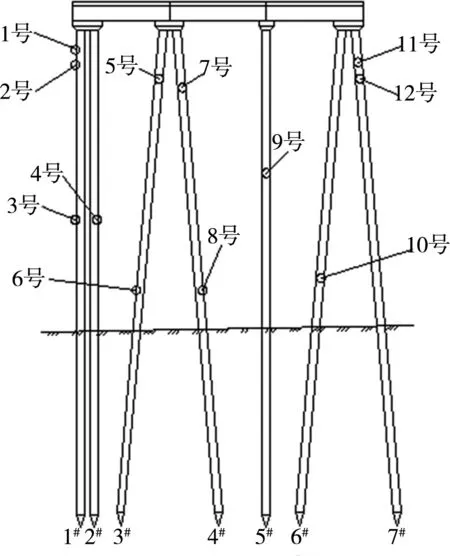
圖7 測點布置

3.3 優化結果評估

采用模態置信度準則進行評估，圖6中，MAC值趨于平緩，其模態置信度矩陣非對角元最大值0.137，在最終模態置信度矩陣(圖8)中明顯可以看出MAC矩陣非對角元均趨近于0，此時模態向量間的夾角趨于正交，說明此時選擇的測點已經能夠識別結構的模態信息，說明這個方案是有效的。

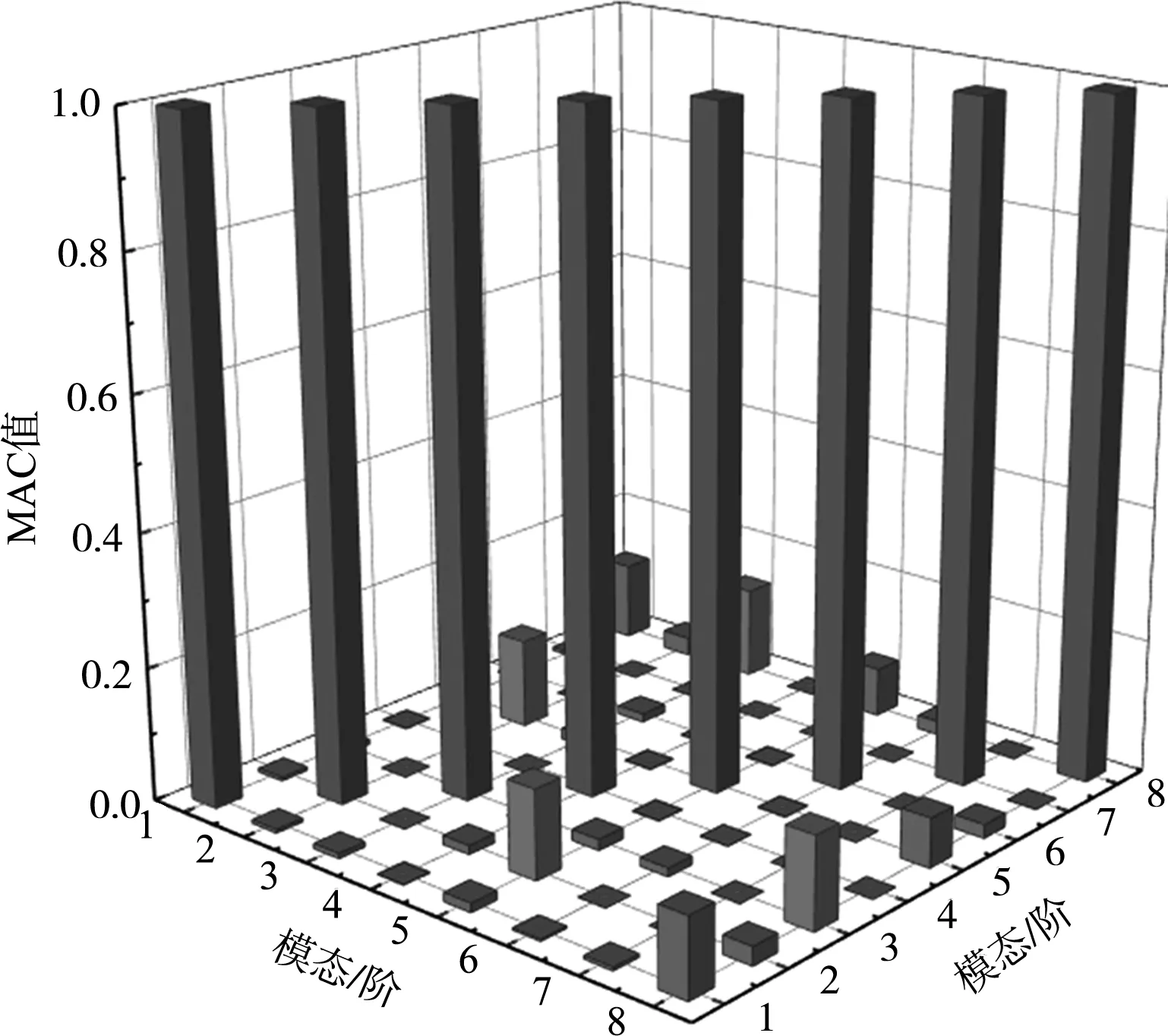
圖8 最終MAC值

4 結論

1)利用傳感器優化布置方法，得到了橫向排架7根樁基的傳感器測點布置結果，對測點布置結果進行評估，模態向量間的夾角趨于正交，證明傳感器布置方案有效。

2)分析7根樁基傳感器測點布置結果發現，橫向排架兩側樁基測點與內側樁基測點相比較多，該布置結果與橫向排架不同樁基的振動特性是一致的。

3)橫向排架考慮了兩側縱梁的約束作用，故較適用于碼頭中部橫向排架的傳感器優化布置。