基于粗大誤差判別準則的測量列數據的處理與優化

唐偉 鐘偉 段國艷

（四川工程職業技術學院電氣信息工程系 四川省德陽市 618000）

1 引言

在測量數據中，無論是用儀器自動測量還是手動測量，總會包含誤差，如粗大誤差、系統誤差、隨機誤差，在這些誤差中粗大誤差對測量數據的準確性危害最大，所以在測量結果中找出粗大誤差并剔除尤為重要。然而關于誤差的算法計算量巨大且復雜，因此，通過軟件程序實現粗大誤差分析與處理將有效提高誤差處理的速度和準確性；因為測量誤差跟測量條件和測量次數等有密切關系，不同的粗大誤差判據有不同的優勢，所以研究根據等精度有限次的測量次數選擇不同的粗大誤差處理算法，對數據的處理有著重要的意義。

2 誤差及相關概念

誤差是測得值與被測量的真值之間的差[1]，其數學表達式為△x=x-x0，其中△x 為誤差，x 為測量值，x0為真值。在測量中，真值本質上是不存在的，實際上常用滿足規定精度的量值來代替真值使用。根據誤差的產生的原因，通常將誤差分為系統誤差、隨機誤差、粗大誤差。

3 粗大誤差算法及特點

粗大誤差是對測量結果的明顯歪曲。產生粗大誤差的原因主要是因為測量人員的疏忽造成讀值或記錄的錯誤，也可能因為外界的原因造成，如振動、熱沖擊等引起測量儀器的示值改變。一旦發現粗大誤差就應該被剔除[1]。判別粗大誤差的方法有多種，同時各具優缺點。

3.1 3σ準則（萊以特準則）

3.2 肖維納準則

圖1：主程序框圖

圖2：3σ 判據子程序框圖

粗大誤差是明顯超統計規律預期值的誤差，如果測量值xi遵循公式（3）的計算結果，則說明引起該誤差的測量值xi為粗大誤差[2]。

λ 實際上是正態分布置信系數，可以通過查肖維納準則表得到，也可以通過查正態分布積分表獲得。

3.3 t校驗準則（羅曼諾夫斯基準則）

判別的依據是：先假設測量列中某個測得值xj為粗大誤差，去掉xj后再計算測量列的算術平均值若式（4）成立則說明xj含有粗大誤差；否則，認為xj不含有粗大誤差。

3.4 格羅布斯準則

圖3：對101 個測量值中的包含粗大誤差的數據剔除仿真結果

將測量值xi，按測得值大小順序排成順序統計量x(i)，即規定選取為判別粗大誤差的臨界值，其中n 為測量次數， 為顯著度。若則說明x(i)包含粗大誤差。否則，x(i)則不含粗大誤差。可以通過程序自動查詢格羅布斯準則表得到。在計算出x(i)為粗大誤差后，應該剔除x(i)并重新計算測得值的個數n。對測得值個數要求不多，判斷的可靠性要求較高的場合比較適用。

4 粗大誤差判別算法的C語言編程實現

4.1 軟件流程框圖

根據不同的測量次數和要求，可選擇不同的判斷依據[3]，最終做出粗大誤差的優化處理選擇。主流程框圖如圖1 所示。主程序根據測量列的數據多少和具體要求選擇相應的粗大誤差處理子程序，每個子程序負責將含有粗大誤差的測得值挑選出來并返回給主程序，主程序剔除含有粗大誤差的數據后對測量數據列重新排列，然后計算出

4.2 各子程序的特點

子程序流程樣例如圖2 所示，本文以萊以特準則判據為例，其余判據子程序處理流程類似圖2。在每個子程序中含有計算及vi和殘余誤差，目的是使主程序簡單。為了保證計算結果的正確性，在程序中引入了算術平均值校核算法。每個子程序結構基本上相同，保證了子程序的簡潔性。子程序基本上分為4 個模塊及查表模塊，計算及校核模塊，判據比較和數據剔除與重排模塊。在數據剔除與重排時先將要剔除的數據暫存，再將數組從剔除點順序搬移，從而構成一個新的數據列，然后將被剔除的數據放于數組的最后，待下次計算時程序不將被剔除的數據包含進去，這樣用最簡單的算法實現了數據的剔除與重排。

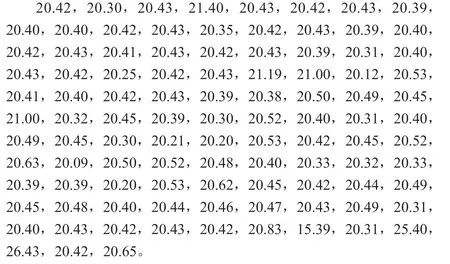
根據圖1 和圖2 流程圖，采用C 語言實現主程序和3σ 粗大誤差判別算法，以給定的101 個測量值為例，完成包含粗大誤差數據的剔除。

主程序主要對粗大誤差處理的子函數調用和處理后數據列的顯示，根據測量列數據的規模，主程序自動調用3σ 粗大誤差判斷算法程序，在子程序中實現了對包含粗大誤差的測量值的剔除和數據列的重新排列，最后將壞值個數返回給主程序，并整理出來不包含粗大誤差的測量值。在Win-Turbo C 環境下仿真運行，可以準確的對測量數據列進行粗大誤差的處理。仿真結果如圖3 所示。

4.3 仿真驗證

在運行結果中，xp 是平均值，dx 是標準差，j 是當前需要處理的數據個數，每剔除一個包含粗大誤差的測量值，j 就會自減1，a是子程序處理過程中定義的數組名，org 代表原測量列數組。因為篇幅所限，這里只給出了程序運行的后期結果。從程序運行的結果可知，j=92 時表示當前還剩92 個測量數據，已經判斷出9 個測量值包含粗大誤差而被剔除，程序繼續對剩下的92 個數據進行計算并判斷，最后又剔除一個，剩下91 個測量數據不包含粗大誤差。

5 結束語

本文針對誤差處理計算量大的問題，用軟件算法實現了對測量數據列中包含有粗大誤差的數據剔除，并完成對原始測量數據的重新排列；同時為提高誤差處理的準確性，根據等精度測量的次數，采用不同的軟件算法對測量數據處理，實現了對粗大誤差精確的剔除。根據文中提出的軟件算法，通過程序仿真驗證，軟件程序計算的快速性和運行結果的準確性達到了工程使用要求。同時該軟件算法程序也可以作為一個獨立的粗大誤差處理工具應用于科研和工程測量中。