無窮維3-李代數的可列結構

周 檬，潘學功，白喜梅

(1.河北軟件職業技術學院軟件技術系，河北 保定 071000；2.河北大學數學系，河北 保定 071002)

1 預備知識

3-李代數[1-3]在理論物理及微分幾何中發揮著重要作用.文獻[4-5]利用交換的結合代數構造出了無限維的3-李代數，研究了無限維單3-李代數與Harish-Chandra模的關系，以及實數域上可微函數空間上的單3-李代數的可列結構.

3-李代數L是域F上具有線性運算[，，]：L∧L∧L→L的線性空間，且滿足?x1，x2，x3，y2，y3∈L，

[[x1，x2，x3]，y2，y3]=[[x1，y2，y3]，x2，x3]+[x1，[x2，y2，y3]，x3]+[x1，x2，[x3，y2，y3]].

設B是3-李代數L的子空間，如果?x1，x2，x3∈B有[x1，x2，x3]∈B，則稱B是L的子代數.

設H是3-李代數L的子代數，如果H是滿足下列條件的極大子代數：

(1) [H，H，H]=0；

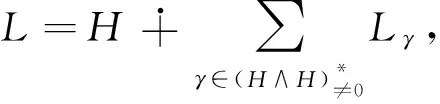
Lγ={x=L|[h1，h2，x]=γ(h1，h2)x，?h1，h2∈H}.

(1)

則稱H是3-李代數L的可列Cartan子代數.如果3-李代數L具有可列Cartan子代數，則稱L為可列3-李代數，等式(1)為L關于可列Cartan子代數H的根空間分解.如果Lγ≠0，則稱γ是關于H的一個根，稱L為根子空間，根的全體Λ={γ∈(H∧H)*-{0}|Lγ≠0}稱為L關于H的根系.

例1 設L是域F上的4維3-李代數，{e1，e2，e3，e4}是L的一組基，L的乘法為

[e1，e2，e3]=e4，[e1，e2，e4]=e3.

直接計算可知H=Fe1+Fe2是L的可列Cartan子代數，L關于H的根空間分解為

L=H+Lγ1+Lγ2，Lγ1=F(e3+e4)，Lγ2=F(e3-e4).

其中Λ={γ1，γ2}?(H∧H)*，γ1(e1，e2)=1，γ2(e1，e2)=-1.

設A是以{Lr，Mr|r∈Z}為基的交換結合代數，其乘法為

LrLs=Lr+s，MrMs=Mr+s，LrMs=0，?r，s∈Z.

定義線性變換δ，ω：L→L，

δ(Lr)=rLr，δ(Mr)=rMr；ω(Lr)=M-r，ω(Mr)=L-r.

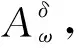
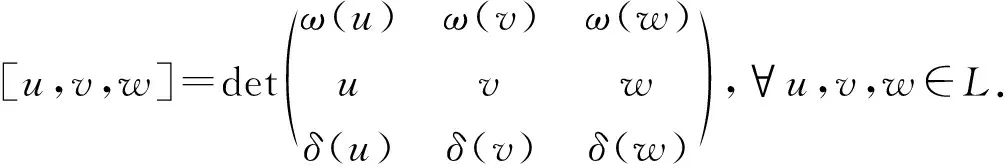
(2)

2 主要結論

設R是實數域，W={fr=yerx，gr=zerx|r∈Z，x，y，z∈R}是三元實函數的集合.顯然，W是所有三元實函數構成的線性空間中的線性無關組，記W在實數域上張成的線性空間為L，則L是以W為基的實數域上的無限維線性空間.

為方便起見，記fr=zerx，gr=yerx，?r∈Z.

定理1 設L是以{fr=yerx，gr=zerx|r∈Z，x，y，z∈R}為基的實數域R上的無限維線性空間，則L按下列運算構成無限維的單3-李代數，記為L?：

(3)

且在基{fr=yerx，gr=zerx|r∈Z，x，y，z∈R}下的乘法表如下：

(4)

證明由文獻[1]可知，L按照運算(3)構成3-李代數，且直接計算可知：

[yelx，yemx，yenx]=[zelx，zemx，zenx]=0，

從而可得乘法表(4).由文獻[4]，在3-李代數L?同構映射

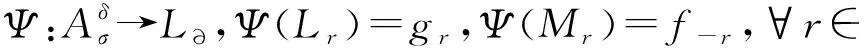
對任意非零整數l0，記Hl0=Rgl0+Rf-l0，即Hl0是以gl0和f-l0為基的L的2維交換子代數，即[Hl0，Hl0，Hl0]=0，且有下列結論：

定理2 3-李代數L?是具有可列Cartan子代數Hl0的可列3-李代數，且關于Hl0的根空間分解為

(5)

γk：Hl0∧Hl0→R，γk(gl0，f-l0)=-(l0+k).

其中根空間Lγk=Rfk+Rg2l0+k，即Lγk是以g2l0+k，fk為基的2維子空間，L?關于Hl0的根系為Λ.

證明因為dimHl0=2，所以[Hl0，Hl0，Hl0]=0.對任意整數k≠l0，由乘法表(4)可知

[gl0，f-l0，gk]=(l0-k)gk，[gl0，f-l0，fk]=(-k-l0)fk.

所以[gl0，f-l0，gk]=0，當且僅當k=l0；[gl0，f-l0，fk]=0，當且僅當k=-l0.因此，對任意a，b∈R，k，l∈Z，k≠l0，l≠-l0，[gl0，f-l0，agk+bfl]=a(l0-k)gk+b(-l-l0)fl=0，當且僅當a=b=0.故H0是L?的可列的Cartan子代數.

定義γk：Hl0∧Hl0→R，γk(gl0，f-l0)=-(l0+k)，k∈Z，k≠l0.則

[gl0，f-l0，fk]=-(l0+k)fk=γk(gl0，f-l0)fk，

[gl0，f-l0，g2l0+k]=(l0-2l0-k)g2l0+k=γk(gl0，f-l0)g2l0+k.

因此，對任意k≠l0，γk是L?關于Hl0的一個根，對應的根空間為Lγk=Rfk+Rg2l0+k，且L?關于Hl0的根系為Λ={γk|k∈Z，γk(gl0，f-l0)=-(l0+k)，k≠l0}，從而等式(5)得證.

定理3 設3-李代數L?關于可列Cartan子代數Hl0的根空間分解為等式(5).則對任意非零r，s，t∈Z≠l0滿足(r-s)2+(r-t)2+(t-s)2≠0，有下列等式成立：

[Lγr，Lγs，Lγt]=Lγr+s+t，γr+γs+γt=γr+s+t∈Λ.

證明由定理2可知，對任意γr，γs，γt∈Λ，有r，s，t∈Z≠l0且

Lγr=Rfr+Rg2l0+r，Lγs=Rfs+Rg2l0+s，Lγt=Rft+Rg2l0+t.

由等式(4)可知

[fr，fs，g2l0+t]=(r-s)f2l0+r+s+t，[fr，g2l0+s，g2l0+t]=(t-s)g4l0+r+s+t，

[fr，g2l0+s，ft]=(t-r)f2l0+r+s+t，[fr，g2l0+s，g2l0+t]=(t-s)g4l0+r+s+t.

因為(r-s)2+(r-t)2+(t-s)2≠0，不妨假設t≠s，r≠s.由上述計算可知

g4l0+r+s+t，f2l0+r+s+t∈[Lγr，Lγs，Lγt].

所以，[Lγr，Lγs，Lγt]=Lγr+γs+γt=Lγr+s+t.證畢.

定理4 3-李代數L?的任意一個可列Cartan子代數都具有形式Hl=Rgl+Rf-l，?l∈Z.因此，3-李代數L?的任意兩個可列Cartan子代數同構.

證明由定理2可知，對任意整數，Hl=Rgl+Rf-l是3-李代數L?的Cartan子代數.再由定理3可得3-李代數L?的任意一個可列Cartan子代數都具有形式H(l).

對任意l，m∈Z，定義線性映射σlm：H(l)→H(m)，

σ(agl)=agm，σ(bg-l)=bg-m，?a，b∈R.

顯然，σ是線性同構，再由H(l)與H(m)都是Abel子代數，所以σ是代數同構.結論得證.