懸浮水輪原理及外界微擾下的系統(tǒng)穩(wěn)定性研究

尹一凡

(北京航空航天大學(xué) 自動(dòng)化科學(xué)與電氣工程學(xué)院，北京 100191)

1 現(xiàn)象分析

在生活中經(jīng)常看到以下現(xiàn)象：在靠近朝上噴水的水柱邊緣小心放置一個(gè)輕質(zhì)物體，在一定條件下，物體將在懸浮的同時(shí)開(kāi)始旋轉(zhuǎn)。通過(guò)實(shí)驗(yàn)觀察出以下特點(diǎn)，一方面，在水流的沖擊下，水輪在豎直面內(nèi)快速旋轉(zhuǎn)，并且轉(zhuǎn)速維持在一個(gè)穩(wěn)定值附近，同時(shí)液體沖擊水輪后出現(xiàn)飛濺現(xiàn)象，之后較強(qiáng)的系統(tǒng)穩(wěn)定性使得體系可以在一定程度上抵抗來(lái)自外部環(huán)境的干擾。通過(guò)觀察高速攝像機(jī)照片發(fā)現(xiàn)，液體在接觸點(diǎn)與物體發(fā)生作用。先以液體流速為變量進(jìn)行了實(shí)驗(yàn)，得出了實(shí)驗(yàn)結(jié)果如圖1所示，從中發(fā)現(xiàn)，液體主要集中離開(kāi)點(diǎn)與液體流速有著很大關(guān)系，隨著流速的增加，液體的離開(kāi)由集中流淌離開(kāi)向鋪灑的方式變化，現(xiàn)象也更為劇烈，而且液體的流淌也更多地從兩側(cè)偏向中間豎直軸線。

通過(guò)對(duì)水流的分析，猜想，水流流向可以分為沿豎直軸線和從輪球兩側(cè)流動(dòng)前進(jìn)這兩種情況，即為圖2中ABC這三條方向，這些方向與物體的外形有著顯著關(guān)系。對(duì)于圖2左圖所舉例的水輪而言，其邊緣垂直的壁面使得AC兩股水流可以忽略不計(jì)，可以視水流為全部經(jīng)過(guò)B的途徑。而對(duì)于圖2右圖所示的情況，即物體兩側(cè)不完全垂直，如圓球、梭型等物體，這時(shí)水流不僅能通過(guò)B途徑，也會(huì)通過(guò)AC途徑前進(jìn)。

通過(guò)對(duì)A/C途徑進(jìn)行分析，其作用除了使B途徑液體量減少外，還在于馬格努斯效應(yīng)的產(chǎn)生。馬格努斯效應(yīng)的含義為：當(dāng)一個(gè)旋轉(zhuǎn)物體的角速度矢量與該物體飛行速度矢量不同向時(shí)，存在垂直于這兩個(gè)矢量的橫向力，使物體的飛行軌跡發(fā)生偏轉(zhuǎn)，橫向力的方向可由右手定則確認(rèn)[1]。

圖2 水輪俯視、平視圖Fig.2 Top view and head-up display of water turbine

圖3 馬格努斯效應(yīng)示意圖Fig.3 Schematic diagram of Magnus effect

在A/C途徑下，物體在旋轉(zhuǎn)角速度下還有著相對(duì)運(yùn)動(dòng)速度，按照馬格努斯效應(yīng)，產(chǎn)生了如圖3所示的橫向力，因此需要在平衡方程中進(jìn)行相應(yīng)的公式修正。同時(shí)，在穩(wěn)定性上，該作用力也使得物體在水平方向上趨向靠近水流沖擊點(diǎn)，使物體不易脫離接觸，縱向上也使得物體維持高度所需的液體作用力更小，使穩(wěn)定性增強(qiáng)。

2 水柱與水輪的位置關(guān)系

對(duì)水輪而言，必須要先由其邊緣與水柱相接觸，使水柱沖擊水輪的下側(cè)，使其產(chǎn)生向上的作用力，使其能夠保持不掉落。同時(shí)，如果作用位置恰好為水輪的正下方，則水輪在理想條件下不會(huì)旋轉(zhuǎn)且會(huì)在所處位置保持平衡。而在實(shí)際情況里，這樣的平衡為不穩(wěn)定平衡，因而不再贅述。

在單側(cè)受到水流沖擊時(shí)，從水平方向來(lái)分析，沖擊點(diǎn)與水輪重心應(yīng)同處于右視基準(zhǔn)面，否則從前視基準(zhǔn)面上分析來(lái)看，水輪所受重力與水柱的作用力不在同一條直線上，無(wú)法滿足平面力系平衡條件，水輪也就無(wú)法處于平衡狀態(tài)。

3 水輪的受力狀況

3.1 僅在沖擊點(diǎn)處存在摩擦力

此時(shí)的受力分析如圖4所示。

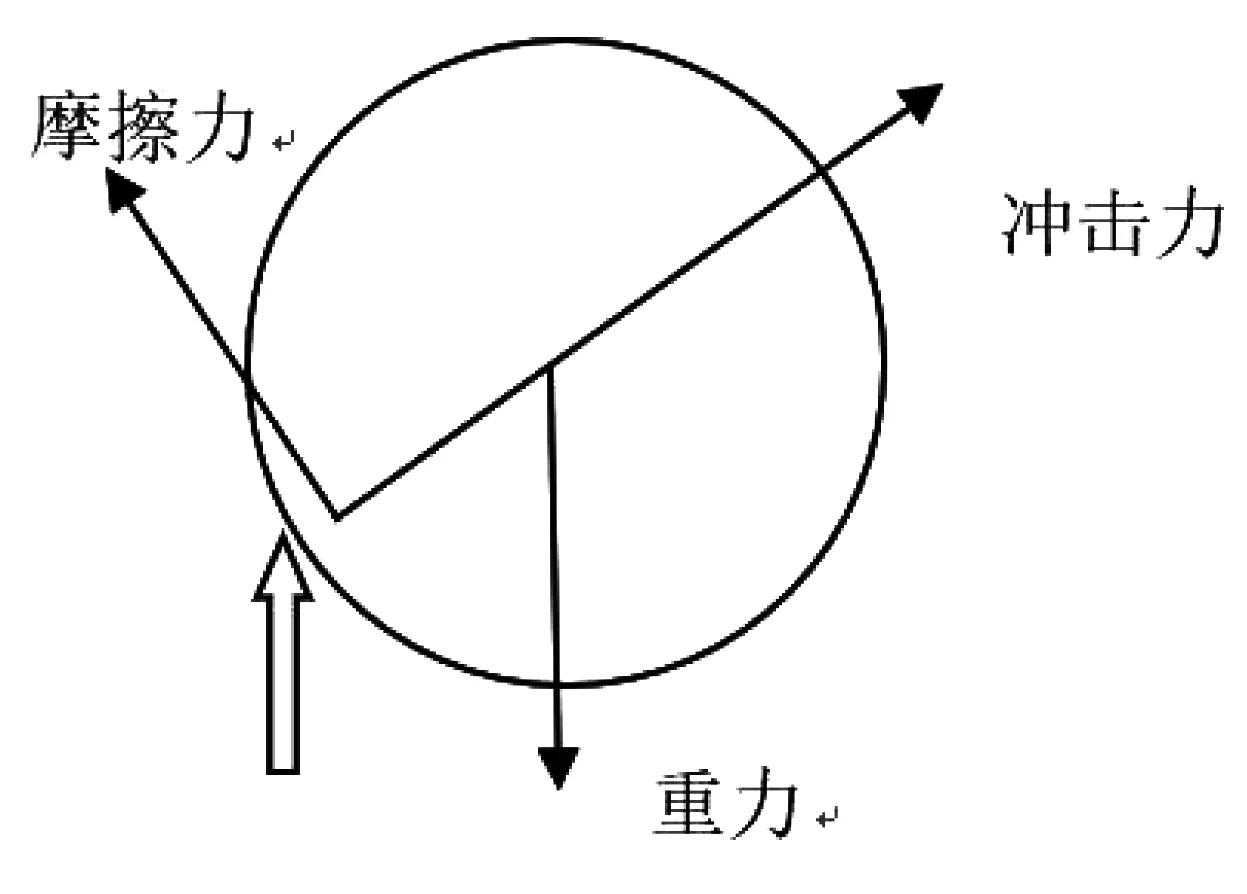
圖4 受力模型假設(shè)Fig.4 Stress model assumptions

假設(shè)沖擊點(diǎn)與圓心連線與水平線夾角為θ，水輪轉(zhuǎn)動(dòng)的角加速度為α，F(xiàn)為沖擊力，F(xiàn)f為摩擦力，R為水輪半徑，m為水輪質(zhì)量，此時(shí)對(duì)其進(jìn)行受力分析：

may=mg+Ffcosθ+Fsinθ=0

max=Fcosθ-Ffsinθ=0

Jα=FfR

其中：

從x、y方向上的受力情況來(lái)看，摩擦力的存在可以使水輪質(zhì)心在鉛錘平面上保持平衡，但由于角加速度α的存在，使水輪旋轉(zhuǎn)不斷加快，在較長(zhǎng)時(shí)間后，在沖擊點(diǎn)的切線方向上，水輪與水柱的速度相同。也就是說(shuō)，兩者間最終會(huì)不存在相對(duì)速度和相對(duì)運(yùn)動(dòng)趨勢(shì)，這樣摩擦力也就不會(huì)產(chǎn)生了。由此看來(lái)，從最開(kāi)始的僅有沖擊力到加入單一的摩擦力來(lái)試圖解決問(wèn)題的模型是不成功的，因此要引入其他的作用力[2]。

3.2 水對(duì)水輪有著多處摩擦力作用

一般情況下，兩個(gè)剛體的碰撞會(huì)使得兩剛體快速接近并迅速分離，中間可能產(chǎn)生了短時(shí)間的法向或切向作用力，而在根據(jù)這一點(diǎn)做出的以上兩種分析均不能解釋?xiě)腋∷喌默F(xiàn)象，因此在新模型中開(kāi)始考慮水的形變帶給水輪受力分析的影響。

考慮到水輪與小球在曲面構(gòu)型上的相似性，以小球?yàn)槔M(jìn)行水柱的沖擊實(shí)驗(yàn)。通過(guò)實(shí)驗(yàn)發(fā)現(xiàn)，當(dāng)水柱沖擊小球的下側(cè)面時(shí)，水柱并沒(méi)有出現(xiàn)像之前猜想的那樣直接彈開(kāi)，而是吸附在了小球表面，以至于將其完全包裹。

圖5 小球模型實(shí)驗(yàn)實(shí)物圖(1)Fig.5 Physical figure of small ball model experiment (1)

如圖5所示，如果繼續(xù)考慮摩擦力的作用，則可以得出以下物理模型：

在初始狀態(tài)下，水柱沖擊水輪后，兩者的切向速度差使得帶動(dòng)水輪旋轉(zhuǎn)，當(dāng)?shù)竭_(dá)平衡狀態(tài)時(shí)，水輪轉(zhuǎn)速保持不變，而水柱在接觸點(diǎn)處的切向速度仍大于水輪的切向速度，在這種情況下，摩擦力對(duì)水輪產(chǎn)生了轉(zhuǎn)動(dòng)加速的力矩。然而，部分水附著在水輪外側(cè)，水輪帶動(dòng)水的作用力的反作用力產(chǎn)生的反向力矩，使得水輪能夠在固定的轉(zhuǎn)速保持平衡[3]。

內(nèi)側(cè)圓代表水輪，外側(cè)圓代表水輪外緣附著的水。同時(shí)，為簡(jiǎn)化模型，假設(shè)，水在同一角度對(duì)應(yīng)的區(qū)域內(nèi)是均勻分布的，而考慮到水在外緣的縱向上可能并不是均勻分布的，可以假設(shè)水的單位質(zhì)量(質(zhì)量的角密度)與角度θ滿足函數(shù)ρ=φ(θ)。

針對(duì)水處于圓心水平線上下兩種情況，分別做出了以下受力分析，其中，T代表水輪對(duì)水的吸附力，F(xiàn)f代表水輪對(duì)水的摩擦力，dmg或G代表任意微小角度dθ所對(duì)應(yīng)的水的重力。

3.2.1 水在中心線下時(shí)(θ<0)

受力分析如圖6所示。

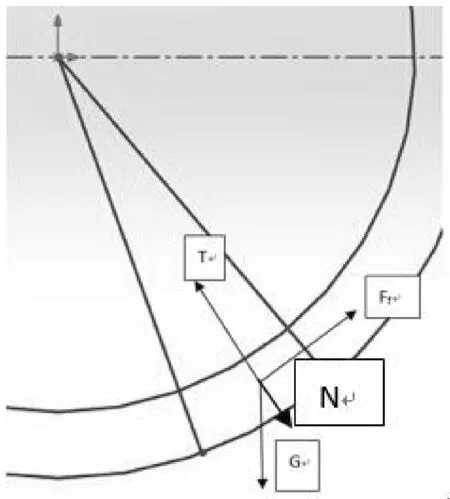
圖6 θ<0時(shí)受力分析Fig.6 Stress analysis when θ<0

在此過(guò)程中，F(xiàn)f可能出現(xiàn)反向情況，便只設(shè)向上為正方向，由此可以建立以下關(guān)系式：

mat=-cosθG+Ff

anm=T-sinθG-N

G=φ(θ)gθdθ

根據(jù)力學(xué)方程，得出動(dòng)力學(xué)規(guī)律如下：

an=ω2R

根據(jù)微分變換可以得出以下式子：

聯(lián)立方程可得：

T-sinθG-N=ω2Rm

其中，當(dāng)水速大于水輪轉(zhuǎn)動(dòng)速度時(shí)：

Ff=μN(yùn)

由此，便可以根據(jù)初始的沖擊點(diǎn)所對(duì)應(yīng)的角度θ0與水柱接觸時(shí)的初始速度來(lái)求解出與之相對(duì)應(yīng)的兩者共速時(shí)的角度θ1與速度ω1。

對(duì)于摩擦力Ff的求解：

3.2.2 水在中心線上時(shí)且在右側(cè)時(shí)(θ>0)

受力分析如圖7所示。

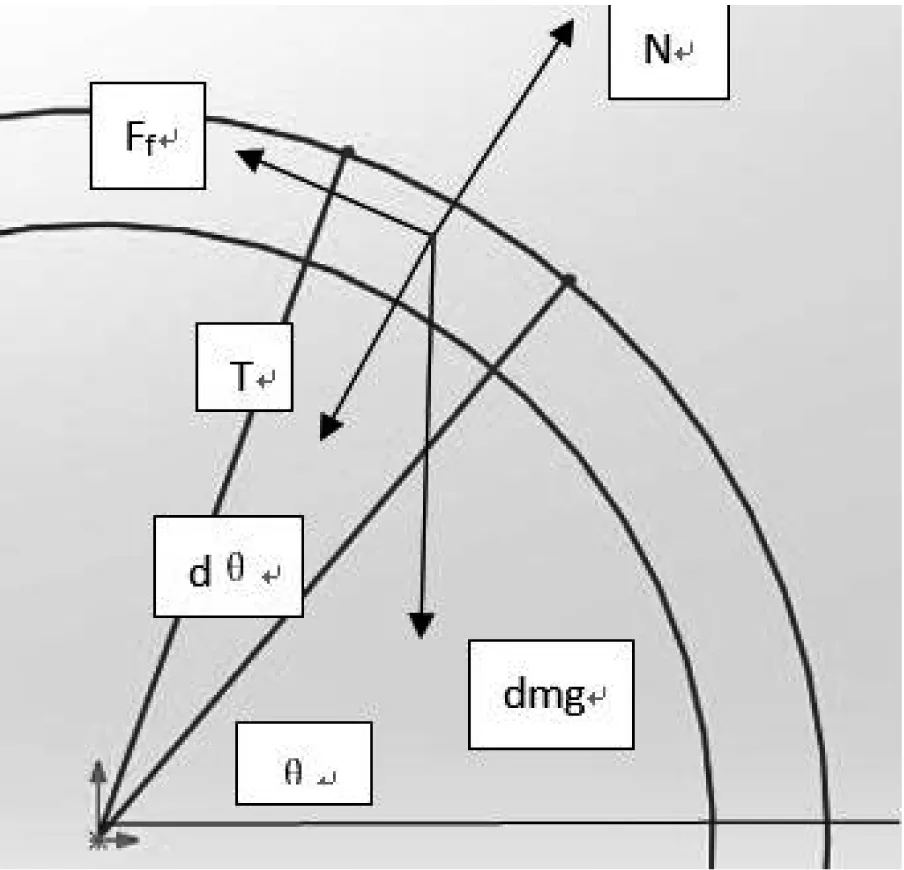
圖7 θ>0時(shí)受力分析Fig.7 Stress analysis whenθ>0

根據(jù)力學(xué)方程，得出動(dòng)力學(xué)規(guī)律如下：

atm=Ff-cosθG

anm=T-N+sinθG

在這一段上，因?yàn)樗嗈D(zhuǎn)速固定，如果假設(shè)附著在水輪上的水流速度處處相等，則ω可視為不變且與水輪轉(zhuǎn)速相等，此時(shí)：

at=0

an=ω2R

聯(lián)立方程可得：

T-N+sinθG=ω2Rm

cosθG=Ff

因?yàn)橘|(zhì)量與角度的關(guān)系式得到：

Ff=cosθgφ(θ)dθ

3.2.3 水在中心線上時(shí)且在左側(cè)時(shí)(θ>0)

由于當(dāng)水被吸附到水輪的左側(cè)時(shí)，其受力分析與水流在右上側(cè)時(shí)完全對(duì)稱(chēng)，而由于水可能會(huì)在這一段上離開(kāi)水輪，因此假設(shè)水在θ2時(shí)離開(kāi)水輪，而過(guò)程中摩擦力的表達(dá)式與之前完全相同。

3.2.4 綜合以上，整體對(duì)水輪進(jìn)行分析

綜上所述，針對(duì)對(duì)水的分析以及牛頓第三定律得出了，水輪所受摩擦力的關(guān)系式為(以逆時(shí)針?lè)较驗(yàn)檎?：

從水輪的所受外力來(lái)看，水對(duì)水輪吸附力的力矩為0，所以僅有摩擦力可以提供力矩。此時(shí)，若以輪質(zhì)心為軸心進(jìn)行分析，摩擦力的力矩只有為0時(shí)，水輪才可能平衡。構(gòu)建力矩力矢的平衡方程為：

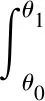
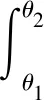
T沖cosθ0=1

T沖sinθ0-Mg=0

其中，水輪與水流的吸附力T是與水的流速、溫度、密度等相關(guān)的函數(shù)[4]。通過(guò)分析得出，作用力T是該作用力可以分為康達(dá)效應(yīng)下的空氣壓力與水輪外緣壁對(duì)液體的沾附作用的合作用力。接著對(duì)空氣壓力進(jìn)行分析，由伯努利方程得出：

考慮到重力對(duì)空氣的作用可近似忽略不計(jì)，同時(shí)貼近液體表面的空氣流速也與液體流速近似相同，便可得出空氣壓力的表達(dá)式：

T可簡(jiǎn)化為Fair(θ)與沾附作用的合力模型，而后者則可以通過(guò)材料間的特性進(jìn)行分析，在此便不再贅述。

φ(θ)也取決于液體流速與水柱流量的關(guān)系，為簡(jiǎn)便運(yùn)算，可假設(shè)T與φ(θ)均為常數(shù)，此時(shí)：

由此，可認(rèn)為該模型是成立的。

3.3 通過(guò)動(dòng)量分析水輪平衡

在之前的三個(gè)模型中，主要依靠對(duì)水輪及水的受力分析來(lái)解決問(wèn)題。現(xiàn)在，通過(guò)構(gòu)建模型和沖量定理來(lái)對(duì)當(dāng)球轉(zhuǎn)速過(guò)高而使水飛濺的情況進(jìn)行定性分析。在之前的模型中，水覆蓋在水輪表面，當(dāng)水流速加快后，水流就不再局限于包裹水輪，而是在隨著水輪轉(zhuǎn)動(dòng)的過(guò)程中沿著水輪的切線飛濺出，如圖8所示，其原理比較接近于研磨金屬板時(shí)飛濺的火花。

圖8 小球?qū)嶒?yàn)實(shí)物圖片(2)Fig.8 Picture of ball experiment (2)

在這種情況下，可以對(duì)水輪及其上面的水做整體定性分析。在沖擊過(guò)程中，水輪始終受到豎直向下的重力帶來(lái)的沖量，因此水必須要提供給水輪以豎直向上的沖量，而兩者在相同時(shí)間內(nèi)大小相等。由牛頓第三定律可知，水輪與水的作用力與反作用力大小相等，方向相反。在這段時(shí)間里，水柱I2受到來(lái)自水輪豎直向下的沖量，這一分析重點(diǎn)在于確保合動(dòng)量在水平方向上的分量為0。由于水流最終的動(dòng)量方向具有不確定性，只要所有動(dòng)量矢量相加的合動(dòng)量方向?yàn)樨Q直方向，則水輪在水平方向上的穩(wěn)定即可得到解釋。

4 水輪的抗微擾分析

水輪穩(wěn)定系統(tǒng)可能會(huì)受到各種外部干擾，可以分為軸向力、豎直力、水流干擾等。

4.1 抗軸向力干擾

4.1.1 干擾恢復(fù)

當(dāng)水柱受到來(lái)自側(cè)面的軸向力干擾時(shí)，水輪會(huì)發(fā)生偏向軸向力方向的傾側(cè)，水流方向也會(huì)隨著水柱的傾側(cè)而發(fā)生傾側(cè)。根據(jù)之前依照沖量定理的分析，當(dāng)受到向右的軸向力時(shí)，水流方向也會(huì)向右傾斜，此時(shí)水流便會(huì)反作用于水輪向左的水平分沖量，水輪在水平方向上便可以得到平衡，并在位移上得到回位。除了從沖量角度進(jìn)行分析，也可以從作用力角度來(lái)分析。當(dāng)水輪受到水平向右的沖量時(shí)，水輪相對(duì)于其所附著的水會(huì)產(chǎn)生向右的相對(duì)速度，此時(shí)水輪便會(huì)受到來(lái)自水的向左摩擦力以使水輪保持平衡。

4.1.2 恢復(fù)的局限性

通過(guò)分析可以看出，只有被附著的水流沿著水柱方向被充分加速再被甩出去才能產(chǎn)生足夠大的反向沖量使水輪平衡。在此過(guò)程中，水的右向加速需要一定時(shí)間，如果加入沖量的時(shí)間過(guò)短，水根本來(lái)不及變向加速，水輪也就無(wú)法在水平?jīng)_量角度上保持平衡。同時(shí)，如果外力的干擾力過(guò)大，使摩擦力無(wú)法平衡外力，則物體會(huì)加大傾斜，直至完全偏離平面，此時(shí)的恢復(fù)力也就無(wú)效了。此外，如果外力的作用點(diǎn)過(guò)于靠近沖擊點(diǎn)，產(chǎn)生的位移使得水柱與水輪的接觸出現(xiàn)偏離，就會(huì)導(dǎo)致附著水流減少，甚至完全脫離水流接觸，使系統(tǒng)根本無(wú)法依靠水流與水輪作用力來(lái)恢復(fù)。

4.2 抗縱向力干擾

4.2.1 干擾恢復(fù)

在豎直方向上，向下的作用力可以視為水輪重量的增大。從突變時(shí)刻到水輪不斷被重新調(diào)整變速到新的平衡轉(zhuǎn)速過(guò)程中，水輪會(huì)在豎直方向上做直線運(yùn)動(dòng)，直至達(dá)到新的穩(wěn)定。而向上的作用力則可以視為水輪質(zhì)量的突變減少，分析過(guò)程基本與向下時(shí)相同，但水輪的質(zhì)心運(yùn)動(dòng)方向和轉(zhuǎn)速變化趨勢(shì)會(huì)相反。

4.2.2 恢復(fù)的局限性

作用力向下時(shí)，主要考慮留給系統(tǒng)的空間是否足夠去調(diào)整。如果水輪距離地面高度過(guò)小，則水輪會(huì)在重新達(dá)到平衡狀態(tài)前撞擊地面，系統(tǒng)也就無(wú)法平衡。而當(dāng)作用力向上時(shí)，平衡的主要問(wèn)題在于作用力與水輪重力及水柱流速的關(guān)系。如果作用力大于重力或理論平衡的位置超出了水柱所能到達(dá)的最大高度，系統(tǒng)也無(wú)法實(shí)現(xiàn)新的平衡。

4.3 水流干擾

4.3.1 干擾恢復(fù)

水流發(fā)生變化主要為暫時(shí)性斷流，水流加強(qiáng)或減弱。對(duì)于暫時(shí)斷流情況，水輪在某一時(shí)刻只會(huì)受重力作用而脫離水流，此時(shí)，水輪會(huì)出現(xiàn)短時(shí)間的落體過(guò)程。而當(dāng)水流加強(qiáng)時(shí)，水輪受到的沖擊力會(huì)突然變強(qiáng)，此時(shí)會(huì)產(chǎn)生向上的沖量，其位置會(huì)上升。在不考慮沖擊力帶來(lái)水平位移的情況下，高度會(huì)上升到新的沖擊點(diǎn)處，水流量與原先處相同。水流減弱時(shí)分析同理。

4.3.2 恢復(fù)的局限性

對(duì)于斷流的存在，在極短時(shí)間內(nèi)，水輪的受力會(huì)存在局部缺失的情況，而且其上面水流的分布也會(huì)出現(xiàn)變化，水輪在水平方向上就會(huì)出現(xiàn)沖量差，會(huì)造成微小的水平偏移。當(dāng)水流速過(guò)大時(shí)，水輪可能會(huì)被短時(shí)激增的沖擊力沖出接觸平面，而造成系統(tǒng)無(wú)法復(fù)原的平衡破壞。當(dāng)水流速過(guò)小時(shí)，水流的作用力可能無(wú)法使水輪保持轉(zhuǎn)動(dòng)或懸浮，會(huì)造成新的失衡。

5 針對(duì)文中假設(shè)的校正

本研究對(duì)水輪表面的水流流量分布做出了常量假設(shè)，現(xiàn)作出更細(xì)致的校正：

設(shè)：在角度θ處飛濺的水量為f(θ)，如果忽略初始沖擊時(shí)損失的水量且水柱的水量為函數(shù)Q(θ)，則其滿足方程：

6 結(jié)論

通過(guò)上述分析表明，水輪與水柱的沖擊點(diǎn)處在水輪質(zhì)心所在縱剖面，否則將無(wú)法在位置上滿足平衡條件。在平衡受力模型的建立中，排除錯(cuò)誤模型，通過(guò)理論證明得出合理的“包裹式摩擦力”物理模型，并通過(guò)合理假設(shè)得出的動(dòng)力學(xué)方程表示出平衡時(shí)的物體狀態(tài)，由定性分析得出平衡時(shí)的沖量條件。在抗微擾分析中，通過(guò)多種外界干擾假設(shè)，分別探究了水輪在不同情況下的動(dòng)態(tài)穩(wěn)定性。最后，對(duì)水流量的常量假設(shè)進(jìn)行校正，用以在日后的實(shí)驗(yàn)中測(cè)出相關(guān)量后對(duì)方程進(jìn)行修正。