二次函數與等腰三角形問題

夏滿

【摘要】初中數學知識可以分為兩大類：一類為代數，其中代表知識為函數;另一類為幾何，其中三角形是初中階段學習的基本圖形之一.函數問題與三角形的結合是常見的問題，主要考查學生對二次函數及三角形的基本性質是否熟練掌握，屬于綜合性較強的問題.

【關鍵詞】二次函數;等腰三角形的性質;等腰三角形的畫法

一、等腰三角形的軸對稱性

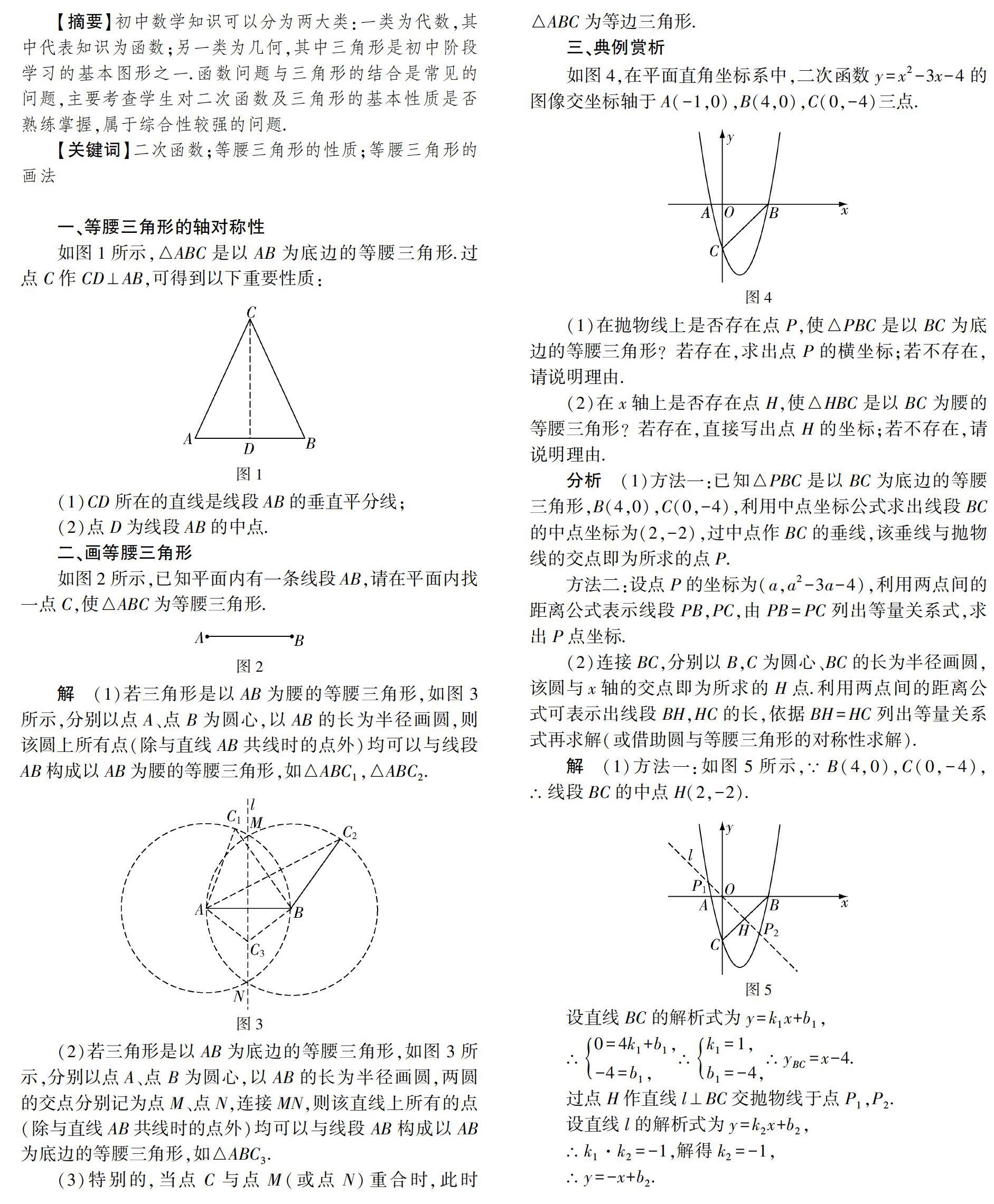
如圖1所示，△ABC是以AB為底邊的等腰三角形.過點C作CD⊥AB，可得到以下重要性質：

（1）CD所在的直線是線段AB的垂直平分線;

（2）點D為線段AB的中點.

二、畫等腰三角形

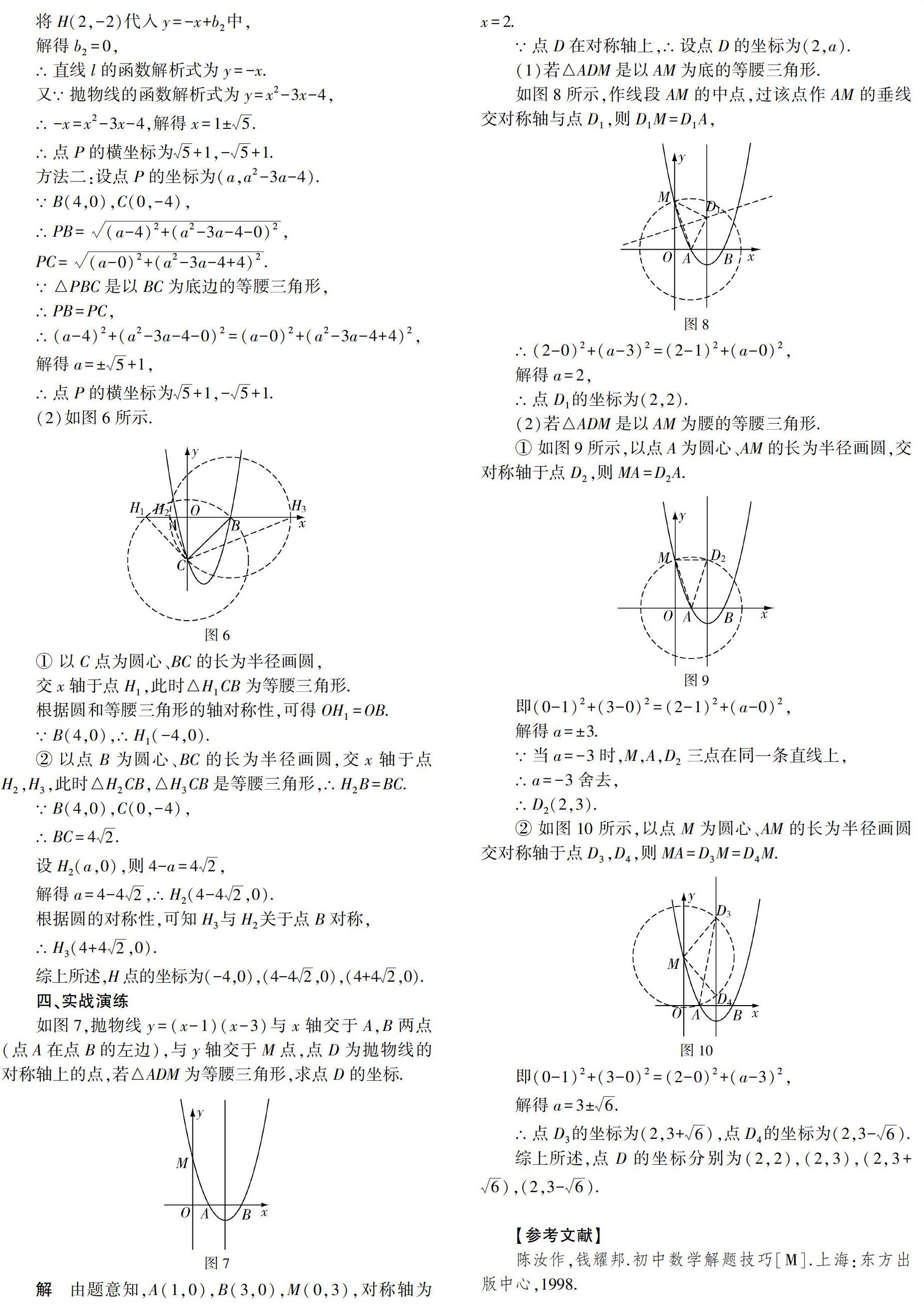
如圖2所示，已知平面內有一條線段AB，請在平面內找一點C，使△ABC為等腰三角形.

解 （1）若三角形是以AB為腰的等腰三角形，如圖3所示，分別以點A、點B為圓心，以AB的長為半徑畫圓，則該圓上所有點（除與直線AB共線時的點外）均可以與線段AB構成以AB為腰的等腰三角形，如△ABC1，△ABC2.

（2）若三角形是以AB為底邊的等腰三角形，如圖3所示，分別以點A、點B為圓心，以AB的長為半徑畫圓，兩圓的交點分別記為點M、點N，連接MN，則該直線上所有的點（除與直線AB共線時的點外）均可以與線段AB構成以AB為底邊的等腰三角形，如△ABC3.

（3）特別的，當點C與點M（或點N）重合時，此時△ABC為等邊三角形.

三、典例賞析

如圖4，在平面直角坐標系中，二次函數y=x2-3x-4的圖像交坐標軸于A（-1，0），B（4，0），C（0，-4）三點.

（1）在拋物線上是否存在點P，使△PBC是以BC為底邊的等腰三角形？若存在，求出點P的橫坐標;若不存在，請說明理由.

（2）在x軸上是否存在點H，使△HBC是以BC為腰的等腰三角形？若存在，直接寫出點H的坐標;若不存在，請說明理由.

分析 （1）方法一：已知△PBC是以BC為底邊的等腰三角形，B（4，0），C（0，-4），利用中點坐標公式求出線段BC的中點坐標為（2，-2），過中點作BC的垂線，該垂線與拋物線的交點即為所求的點P.

方法二：設點P的坐標為（a，a2-3a-4），利用兩點間的距離公式表示線段PB，PC，由PB=PC列出等量關系式，求出P點坐標.

（2）連接BC，分別以B，C為圓心、BC的長為半徑畫圓，該圓與x軸的交點即為所求的H點.利用兩點間的距離公式可表示出線段BH，HC的長，依據BH=HC列出等量關系式再求解（或借助圓與等腰三角形的對稱性求解）.

解

（1）方法一：如圖5所示，∵B（4，0），C（0，-4），∴線段BC的中點H（2，-2）.

【參考文獻】

陳汝作，錢耀邦.初中數學解題技巧[M].上海：東方出版中心，1998.