融入邏輯關系的項目調度遺傳算法

劉 堯,宋元斌,李云祥

(上海交通大學 船舶海洋與建筑工程學院,上海 200240)

0 概述

隨著工程項目規模的不斷擴大,解決施工進度計劃的快速編制問題變得越發重要。施工進度計劃的快速編制主要包括兩項關鍵技術,即施工順序的表述模型和與之對應的求解算法。施工順序知識用于推導進度計劃編制中施工活動的先后順序,為工程模型到數學模型的轉換提供依據;調度模型的求解是一種典型的NP難問題,根據不同的調度模型有不同的求解方法。

復雜施工排序方案中的表述問題主要分為兩類。第一類為施工活動的時間順序表述問題,主要用于推理進度計劃中的施工活動先后順序。文獻[1]用時間區間描述活動的持續狀態,并定義了2個時間區間之間的13種關系。后續研究者在其基礎上擴展引入了最大時間間隔[2]、負時間間隔[3]和時間約束柔性[4]等概念,解決了施工活動順序表達上的大部分難題。第二類為施工計劃中的邏輯關系表述問題,即施工活動與時間關系間的邏輯關系,許多學者對其進行了研究。文獻[5]使用Disjoint描述2個時間關系之間存在“Or”邏輯關系。文獻[6]用包含(→)、等價(?)和異或(?)3個邏輯運算符來描述邏輯關系。文獻[7]提出活動之間的互斥和共存關系,用以描述備擇施工方案之間的關系。

研究者在調度模型的算法設計中,會依據時間約束[8]、資源約束[9]等條件改進算法,也會直接使用調度工具[10]進行求解。文獻[11]在電網規劃上使用布爾變量來簡單表示區域電網投運與否的狀態,從而計算電網的最小成本。文獻[12]將傳統遺傳算法與模擬退火算法相結合來解決Web服務組合質量優化問題。文獻[13]用改進的遺傳算法對BP神經網絡的初始權重進行賦值,用以加快神經網絡的收斂速率。上述規劃模型采用互相獨立的布爾變量表示簡單邏輯關系進行遺傳算法的改進設計,均未解決復雜邏輯關系的計算難題。

求解調度模型主要分為精確式算法和啟發式算法。精確式算法受線性規劃求解器容許決策變量數目的限制,在求解中小規模的調度問題時具有速度快、結果精確的優點,但在求解帶有大量邏輯關系的超大型復雜調度模型時,卻表現出時間效率低下的問題,不能滿足一些規模龐大的優化調度問題求解需求。啟發式算法主要用于快速有效地求解大規模問題的較優解。因此,采用啟發式算法求解帶有較多邏輯關系的復雜調度問題是合理的選擇。

遺傳算法是一種經典的啟發式算法,被廣泛應用于工程計劃,如施工項目[14]、流水作業[15]、高速公路建設[16]等。為了滿足特定領域的需求,研究者也會對遺傳算法進行相應改進。文獻[17]通過改進交叉算子,解決了含有多個目標的最優化模型求解問題。文獻[18]在處理裝配式建筑構件運輸問題上,加入運輸節點的權重計算,加快種群的收斂速度。由于上述算法沒有考慮工程模型中的備擇和依存關系,因此難以描述復雜調度模型中的邏輯關系。

本文基于文獻[6]的邏輯運算符,增加了邏輯符XOR、XNOR和IF-THEN來表示活動之間和時間關系之間的邏輯關系,編程實現復雜調度模型到混合整數規劃模型[19]的自動轉換,并提出一種解決該問題的改進遺傳算法,采取基于工程邏輯關系布爾變量劃分的順序編碼方式,將染色體劃分為獨立變量和半獨立變量編碼基因段,從而解決帶有大量依賴邏輯關系的調度模型求解問題。

1 調度模型中邏輯關系的表述

本節在探究時間關系之間的互斥(XOR)與共存(XNOR)邏輯關系基礎上,提出用“IF-THEN”表示活動或時間關系之間存在的依賴邏輯關系,同時探究將其轉化進入混合整數線性規劃的數學理論方法。文中符號說明如表1所示。

表1 符號定義說明

為說明包含時間關系的邏輯關系,本文引入布爾決策變量ER(i,j)用以描述時間關系之間的邏輯關系,下標中R表示該變量為時間關系的布爾變量,(i,j)表示此為描述活動i和活動j的時間關系。如果一個時間關系R(i,j)被選擇執行,則對應的決策變量ER(i,j)被賦值為1,否則賦值為0。

(1)

邏輯關系的線性約束表達如表2所示。

表2 邏輯關系與線性約束的關系

Table 2 Relationship between logical relations and linear constraints

邏輯關系線性約束活動i與j為互斥關系Ei + Ej = 1活動i與j為共存關系Ei = Ej活動i與j為依賴關系Ei ≤ Ej活動i與時間關系R(j,k)為互斥關系Ei + ER(j,k) = 1活動i與時間關系R(j,k)為共存關系Ei = ER(j,k)活動i與時間關系R(j,k)為依賴關系Ei ≤ ER(j,k)時間關系R(i,j)與R(k,l)為互斥關系ER(i,j) + ER(k,l) = 1時間關系R(i,j)與R(k,l)為共存關系ER(i,j) = ER(k,l)時間關系R(i,j)與R(k,l)為依賴關系ER(i,j) ≤ ER(k,l)

2 復雜調度模型的建立與求解

為克服精確式算法求解帶有大量邏輯關系的超大型工程存在的不足,本文設計了基于布爾變量劃分的順序編碼方式,在遺傳算法中對違反約束規則的個體進行了修正。

2.1 調度模型

施工調度計劃最主要的任務之一是確定最短工期下的施工排序方案。本文的調度模型優化目標使項目結束時間FP最小。計算工期的混合整數線性規劃模型如下:

目標函數如式(2)所示。

MinZ=FP

(2)

約束條件如式(3)～式(17)所示。

a′×Si-a′×Sj+Di+L(i,j)≤0

?R(i,j),1≤i≤n,1≤j≤n

(3)

a′×Si-a′×Sj+EAi×Di+L(i,j)≤0

?R(i,j),1≤i≤n,1≤j≤n

(4)

a′×Si-a′×Sj+Di+L(i,j)-M(1-ER(i,j))≤0

?R(i,j),1≤i≤n,1≤j≤n

(5)

a′×Si-a′×Sj+EiA×Di+L(i,j)-

M(1-ER(i,j))≤0,?R(i,j),1≤i,j≤n

(6)

Si≥0,i=1,2,…,n

(7)

Si+Di≤Fp,i=1,2,…,n

(8)

Ei+Ej=1,iXORj

?i,j,1≤i≤n,1≤j≤n

(9)

Ei=Ej,iXNORj,?i,j,1≤i≤n,1≤j≤n

(10)

ER(i,j)+ER(k,l)=1,R(i,j) XORR(k,l)

?R(i,j),R(k,l),1≤i,j,k,l≤n

(11)

ER(i,j)=ER(k,l),R(i,j) XNORR(k,l)

?R(i,j),R(k,l),1≤i,j,k,l≤n

(12)

Ei≤Ej,IFiTHENj

?i,j,1≤i≤n,1≤j≤n

(13)

Ei≤ER(k,l),IFiTHENR(k,l)

?i,1≤i≤n,1≤k,l≤n

(14)

ER(k,l)≤Ej,IFR(k,l) THENj

?i,1≤k,l≤n,1≤j≤n

(15)

ER(i,j)≤ER(k,l),IFR(i,j) THENR(k,l)

?i,j,1≤i,j,k,l≤n

(16)

Ei,Ej,ER(i,j),ER(k,l)∈{0,1}

(17)

目標函數是項目工期的最小化,式(3)是2個確定執行的活動之間的時間關系約束的一般形式,式(4)～式(6)是活動時間關系的邏輯表示,式(7)限定了所有活動的開始時間均大于等于0,式(8)則限定所有活動必須在工期之內完成,式(9)～式(16)是2個備擇活動或備擇時間關系之間的邏輯關系表達式,式(17)定義各決策變量為布爾變量。

2.2 遺傳算法求解

基于布爾變量劃分的順序編碼方式,本節提出一種遺傳算法,將染色體分為獨立變量和半獨立變量編碼基因段,以原調度模型中的最短工期的倒數為適應度函數,進行最優解的搜索,編程實現帶有較多邏輯關系調度模型的啟發式求解。該算法借鑒動態規劃的思想[20-22],采用單點交叉與變異,存儲了父代種群運算結果,將新生成的子代與父代進行比對,相同編碼即可采用同樣的適應度運算結果,有效提高了遺傳算法的運算效率。在遺傳操作后進行沖突檢測,消除由于種群初始化、交叉和變異操作生成的違反約束規則的個體。

2.2.1 布爾變量的順序編碼

在解決傳統調度優化問題的大多數遺傳算法中,染色體編碼中的各個基因相互獨立,迭代過程中各基因取值不受其他基因取值的影響,但式(13)～式(16)表明決策變量Ei及ER(i,j)之間存在依賴關系。為描述該依賴關系,本文在基因鏈編碼設計中加入半獨立變量。

在本文模型中所有布爾變量共分為3類:獨立變量,半獨立變量和派生變量。獨立變量指在眾多變量中不受其他變量取值影響的變量,半獨立變量指在其他變量確定后仍有一定取值范圍的變量,派生變量指在獨立變量和半獨立變量確定后取值就確定的變量。

本文算法采用基于布爾變量劃分的順序編碼方式,將整個編碼區域分為獨立變量區域(I區)和半獨立變量區域(II區)。

1)布爾變量編碼規則

在遺傳算法的改進過程中,為了保證后續進行遺傳編碼的沖突檢測和修正,確保新產生的染色體的有效性,設計編碼規則如下:

(1)在約束中被運算的次數多的布爾變量優先編碼并賦值。

(2)在運算次數相同的條件下,模型中原始序號靠前的布爾變量優先編碼并賦值。

(3)等式約束條件分別對應一對獨立變量與派生變量,不等式中對應的約束條件Ei≤Ej中,Ei優先考慮是否為獨立變量。

假定模型中有n個獨立變量(Ii表示第i個獨立變量),m個半獨立變量(Sj表示第j個半獨立變量),基于布爾變量劃分的順序編碼方式將染色體編碼基因鏈分成I區編碼區和II區編碼區,如圖1所示。

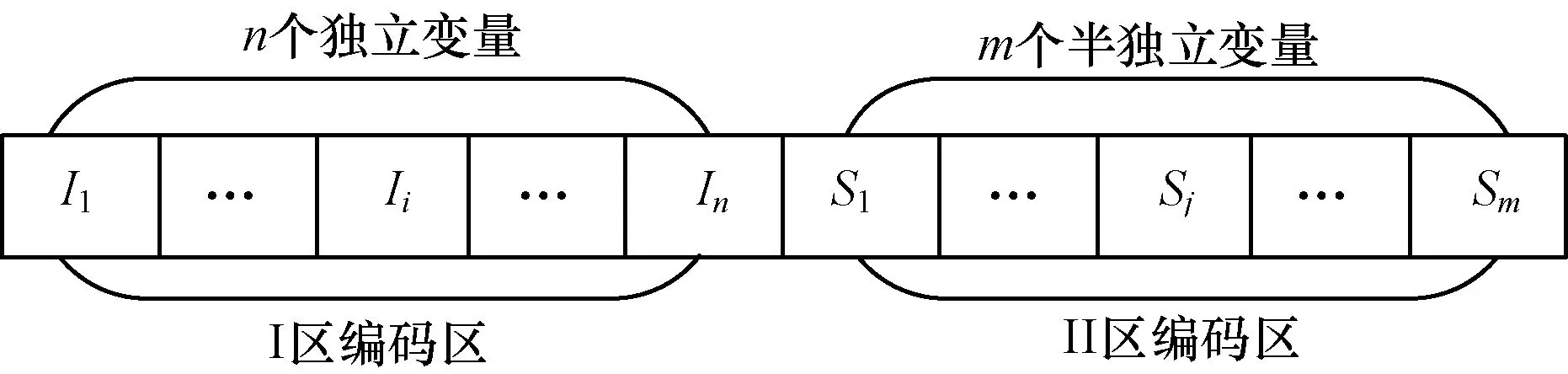
圖1 染色體編碼基因鏈

在包含n個變量的等式或不等式中,總會存在一個獨立變量和派生變量,其余變量為半獨立變量。

在該編碼原則下,II區編碼基因改變對其他基因位的影響程度將呈降序排列,后續沖突檢測中對II區編碼自前向后依據約束規則進行修改,這樣可以確保修改后的染色體仍然是有效的個體,同時也可保證對染色體編碼影響最大的編碼改動最小,盡量保持原編碼的有效性。該編碼以線性時間檢測修改染色體,相對于算法適應度線性規劃求解部分的速度影響可以忽略不計。

2)編碼規則示例

為形象化展示本文算法染色體順序編碼規則,本節以一個項目調度算例來說明,圖2為該工程算例調度網絡。

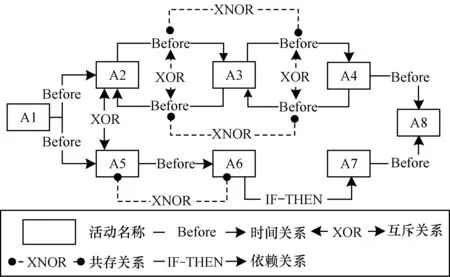
圖2 包含時間關系和邏輯關系的工程算例

本算例包含互斥、共存和依賴邏輯關系,式(18)～式(20)表示3個互斥邏輯關系,式(21)～式(23)表示3個共存邏輯關系,式(24)表示一個依賴邏輯關系。

E2+E5=1

(18)

ER(2,3)+ER(3,2)=1

(19)

ER(3,4)+ER(4,3)=1

(20)

ER(2,3)=ER(3,4)

(21)

ER(3,2)=ER(4,3)

(22)

E5=E6

(23)

E6≤E7

(24)

為了求出最少個數的獨立變量,設目標函數為:

?i,R(j,k),1≤i,j,k≤n

(25)

計算求出一組符合本文算例布爾變量的可行解為:獨立變量E5和ER(2,3),派生變量E2、E6、ER(3,2)、ER(3,4)和ER(4,3),半獨立變量E7。根據基于布爾變量劃分的順序編碼方式和變量編碼賦值規則,算例的染色體編碼基因鏈如圖3所示。

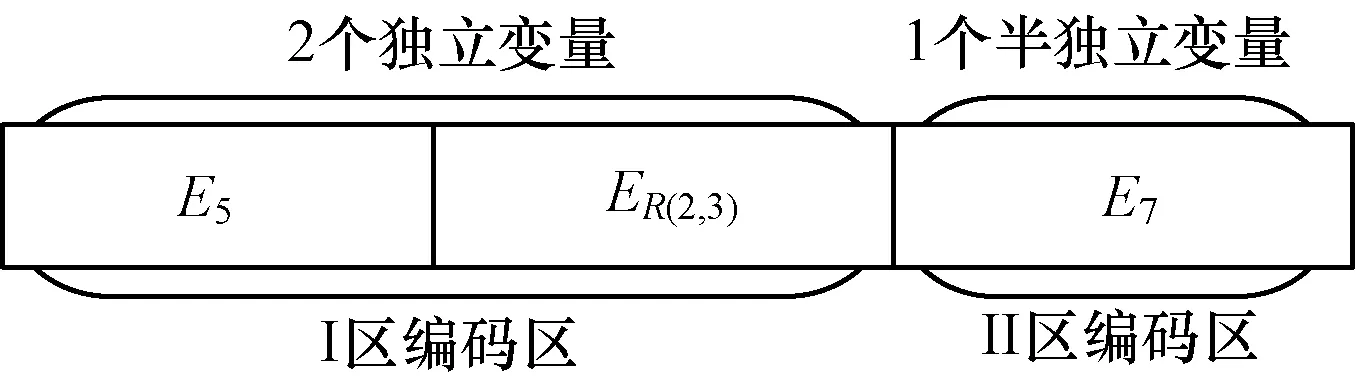
圖3 算例中染色體編碼基因鏈

2.2.2 遺傳算子

本文針對施工活動和時間關系間存在的大量邏輯關系,采用了獨立變量和半獨立變量的順序編碼機制。

1)算子的選擇

調度模型的目標是最小化項目工期,求解過程需要最小化適配值,在選擇過程中將使用輪盤賭的選擇操作,因此,采用項目總工期的倒數作為適配值。令f(i)表示個體的適配值,在總數為λ的種群(POP)中個體生存概率為:

(26)

2)交叉算子

本文采用編碼基因鏈單點交叉,即各對應編碼基因段分別交叉的方式對個體進行交叉操作。

3)變異算子

本文采用編碼基因鏈基本點位變異。

2.2.3 沖突檢測與消除

傳統遺傳算法采用2種方法求解染色體中存在互相約束的基因編碼問題:

方法1在編碼時剔除掉能夠根據其他編碼推理得到的變量編碼,之后在適應度計算時再對被剔除編碼進行計算,得到適合該染色體的最佳適應度值和染色體編碼。

方法2在遺傳操作之后檢測染色體編碼中是否存在沖突的基因編碼,如果存在則將該染色體舍去或者設置染色體適應度值為極低。

在大型復雜施工項目中,II區編碼數量較大,方法1雖然可以降低迭代次數,但每一代種群的求解效率將極低。方法2會產生大量不可行的染色體編碼,導致算法收斂過快,因此,需要設置比較大的種群數量來保證種群在整個迭代過程中的多樣性,在工程規模較大時,求解效率無法令人滿意。

本文算法在進行適應度計算之前,依據I區獨立變量和II區其他半獨立變量的約束不等式進行反饋修正II區基因段,消除違反約束條件的個體。在沖突檢測之后,染色體編碼的I區獨立編碼部分不受影響,保留原染色體的I區編碼的有效性,II區編碼的修改程度依次降低。該修正使II區部分無效的編碼變為有效,同時也保留了有效的編碼區域。

2.2.4 調度問題的遺傳算法描述

采用本文遺傳算法計算最短工期的流程如圖4所示。

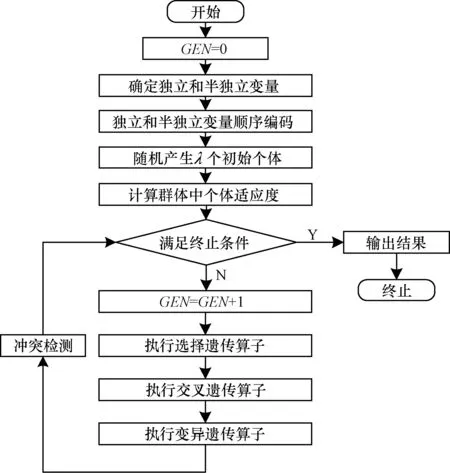
圖4 遺傳算法計算最短工期的流程

Fig.4 Flowchart of genetic algorithm calculating the shortest construction period

本文遺傳算法的具體實現步驟如下:

步驟1根據布爾變量順序編碼機制,對調度模型中的獨立變量和半獨立變量進行順序編碼,并隨機產生初始種群POP,種群規模為pop,當前代數為GEN=0。

步驟2計算種群中的個體適配值。

步驟3GEN=GEN+1。

步驟4根據交叉概率參數Pc,選出參與遺傳操作的子種群POPope,每個個體的染色體由獨立變量基因段和半獨立變量基因段構成。

步驟5采用各對應編碼基因段分別交叉的方式對POPope中個體進行交叉操作,得到子代種群CHI。

步驟6根據變異規則和概率Pm對子代種群CHI中個體的每個基因段進行變異操作。

步驟7將CHI中基因段組合成個體,計算其中個體的適配值。

步驟8POP=POP∪CHI。

步驟9通過選擇操作從POP中選出λ個個體作為下一代的種群。

步驟10檢測II編碼區,依據I編碼區獨立變量的約束規則進行修正。

步驟11如果GEN≥Gmax,終止算法,否則轉步驟3。

3 算例仿真

本文在MATLAB(R2015b)下,分別編寫了精確算法與遺傳算法的求解方法。精確解將使用線性求解規劃器計算得到模型的最短工期解,用于驗證遺傳算法的結果正確性。遺傳算法的主要參數如表3所示。

表3 遺傳算法參數設置

某后張預應力橋梁采用平衡懸臂法進行施工,2個移動平臺用來支撐在建設過程中橋墩兩側的橋梁分段,橋梁結構呈中跨對稱結構。平衡懸臂結構從中間橋墩向兩邊施工的過程中,為保持橋梁結構的穩定,在任何時候都必須保證橋梁結構兩邊的澆筑分段數量之差不大于1 。由于左右平衡懸臂結構的對稱性,本文只研究左邊結構的施工過程,用于測試調度模型和算法的實用性。本工程共包含25個施工活動,調度網絡如圖5所示。

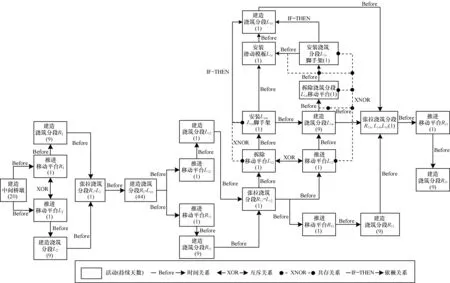
圖5 案例調度網絡

通過模型轉換引擎,生成混合整數規劃模型為:

MinZ=Fp

(27)

其約束條件為:

S1+20≤S2

(28)

S1+20≤S3

(29)

S2+1-(1-ER(2,3))×M≤S3

(30)

S3+1-(1-ER(3,2))×M≤S2

(31)

S2+1≤S4

(32)

S3+1≤S5

(33)

S4+9≤S6

(34)

S5+9≤S6

(35)

S6+1≤S7

(36)

S7+44≤S8

(37)

S7+44≤S9

(38)

S8+1≤S10

(39)

S9+1≤S11

(40)

S10+9≤S12

(41)

S11+9≤S12

(42)

S12+1≤S13

(43)

S12+1≤S14

(44)

S12+1≤S21

(45)

S13+E13≤S15

(46)

S14+E14≤S16

(47)

S15+E13≤S16

(48)

S15+E13≤S19

(49)

S16-(1-E14)×M+9≤S17

(50)

S16+9≤S23

(51)

S17+E14-(1-E14)×M≤S18

(52)

S18+E14-(1-E14)×M≤S19

(53)

S19+1≤S20

(54)

S20+9×E20≤S23

(55)

S21+1≤S22

(56)

S22+9≤S23

(57)

S23+1≤S24

(58)

S24+1≤S25

(59)

ER(2,3)+ER(3,2)=1

(60)

E13+E14=1

(61)

E13≤E20

(62)

E14≤E20

(63)

ER(2,3),ER(3,2),E13,E14,E20∈{0,1}

(64)

Si+Di≤PF,i=1,2,…,n

(65)

Si≥0,i=1,2,…,n

(66)

當采用精確算法求解時,計算得出該案例的最短工期為110天。在調度模型中備擇活動和時間關系被選擇的情況為E13=1,E14=0,ER(2,3)=1,ER(3,2)=0,ER20=1。

采用遺傳算法求解的結果如圖6所示。由于本案例活動數較少,包含的邏輯關系也較少,在迭代到12代時,整個種群平均天數已經達到最短工期,種群天數已經趨于收斂。計算得到的最短工期仍為110天,案例中布爾變量的計算結果和精確解相同。

在共228個活動的調度模型中采用遺傳算法求解,可以發現在遺傳代數迭代到45代時,整個種群平均適配天數已經趨于收斂,可得最小工期為689天,和精確解結果相同。

為驗證設計的遺傳算法適用于帶有大量邏輯關系的超大型復雜調度模型,本文通過增加邏輯關系的數量和項目規模的來驗證遺傳算法收斂效果。分別在活動數為500、1 000、2 000的模擬工程仿真中對比精確解、傳統遺傳算法和本文算法的求解效率,其中,傳統遺傳算法A編碼部分將只考慮獨立變量,傳統遺傳算法B將在進行遺傳操作之后對所得染色體進行有效性分析,如果染色體無效將會選擇新的父染色體進行交叉變異操作,計算結果取3次測試平均值并取整,結果如表4所示。

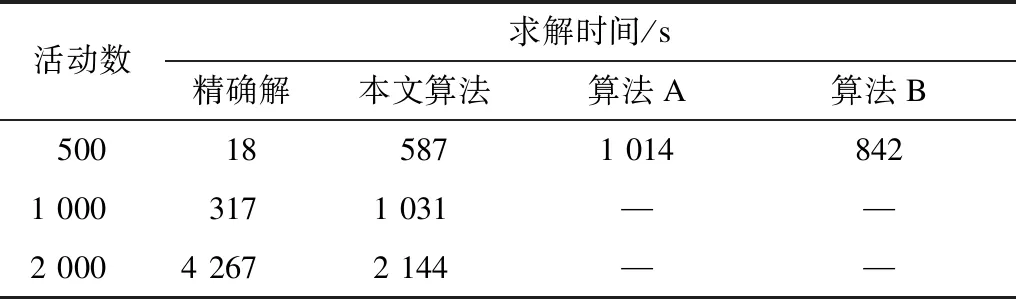
表4 模擬案例中的求解效率對比

由表4可以看出,雖然精確解對中小規模的調度模型求解速率確實較快,但是隨著工程規模的擴大,求解效率逐漸弱于本文算法。傳統遺傳算法A受大型工程中約束關系過多的影響,求解速度極慢,無法在有效時間內求解;傳統遺傳算法B對大型工程求解過程中出現交叉變異操作產生的有效染色體概率極低的情況,種群進化速度緩慢,收斂速度降低,在長時間內無法得到收斂結果。

4 結束語

本文在互斥與共存邏輯關系的基礎上引入IF-THEN來進一步描述依賴關系,討論3種邏輯關系之間的內在聯系,探索更為底層的邏輯關系表述方法。在此基礎上,擴展調度模型到混合整數規劃模型的轉換規則,并分析邏輯關系的計算規則,實現模型間的自動轉換。通過對模型中的邏輯關系變量進行分段編碼,在變異操作后加入沖突檢測環節,消除由種群初始化與遺傳操作產生的違反約束個體。編程實現本文算法的自動求解,并與精確算法進行對比,仿真結果表明,隨著工程規模的擴大,該算法能有效縮短求解工期的時間。下一步將探究染色體編碼中的層級劃分概念,通過改進遺傳算子,在保證近似解合理的情況下提高算法效率。