玻色-愛因斯坦凝聚中的環狀暗孤子動力學*

郭慧 王雅君 王林雪 張曉斐?

1) (中國科學院國家授時中心時間頻率基準重點實驗室, 西安 710600)

2) (中國科學院大學天文與空間科學學院, 北京 100049)

3) (陜西科技大學文理學院, 西安 710021)

環狀暗孤子最早是在非線性光學系統中理論預言并實驗實現的一種二維孤子類型.跟通常的二維孤子(如條紋孤子)相比, 環狀暗孤子具有更好的穩定性和更加豐富的動力學行為.玻色-愛因斯坦凝聚由于其高度可調控性為研究環狀暗孤子提供了一個全新的平臺.本文結合玻色-愛因斯坦凝聚和孤子研究的現狀, 綜述玻色-愛因斯坦凝聚中環狀暗孤子的解析解、穩定性調控及其衰變動力學等方面的研究進展.首先介紹了一套變換方法將均勻系統中非線性系數不隨時間變化的環狀暗孤子解析解推廣到諧振子外勢下非線性系數隨時間變化的環狀暗孤子解析解; 然后討論在形變擾動下環狀暗孤子的穩定性相圖, 并介紹了如何利用周期調制的非線性來增強環狀暗孤子的穩定性; 此外, 還重點討論了環狀暗孤子衰變導致的渦旋極子動力學以及斑圖形成.

專題：非線性物理

1 引 言

孤子是一種存在于非線性系統中的奇異拓撲激發.孤子的概念最早是在1965年由Zabusky和 Kruskal[1]在研究Korteweg-de Vries方程時提出的.穩定的孤子在傳播過程中可以保持形狀、幅度和速度不變.孤子廣泛存在于經典和量子流體、非線性光學、等離子體等各種非線性系統中[2,3],引起了不同領域科學家的廣泛關注[4?10].自從1995年超冷原子玻色-愛因斯坦凝聚(BEC)在實驗上實現[11?14]以來, BEC中的孤子性質及其動力學成為冷原子物理領域的重要課題.跟其他非線性系統(如經典流體等)相比, BEC具有高度可操控性, 可以通過光場、磁場、電場跟冷原子耦合來改變BEC的幾何結構、維度、外勢以及相互作用等[15?21],從而為孤子的理論和實驗提供了優越的平臺, 并為孤子研究注入了新的活力[2,22?25].

BEC中的孤子通常可以分為亮孤子和暗孤子.所謂亮孤子是指在BEC背景上激發的穩定的局域密度凸起結構, 而暗孤子是指在BEC背景上激發的穩定的局域密度凹陷結構.BEC中是否存在穩定的亮孤子或者暗孤子一般取決于原子之間的相互作用.對于吸引相互作用的系統一般存在亮孤子, 而對于排斥相互作用的系統一般存在暗孤子.早在BEC實驗實現以前, 科學家已經從理論上預言了該系統中可能存在穩定的孤子[26].1999年Denschlag等[27]和Sanpera等[28]利用相位刻印技術 (phase imprinting technique)在超冷23Na和87Rb原子的BEC中觀察到暗孤子, 標志著孤子這一非線性現象在BEC系統中的首次實驗實現.兩個研究組分別用了不同的原子種類, 即23Na和87Rb.由于這兩種原子之間的相互作用都是排斥相互作用, 因而亮孤子一般是不穩定的.但當排斥相互作用和孤子的相位梯度達到某種平衡時, 系統中允許存在穩定的暗孤子.隨著Feshbach共振技術在超冷原子 BEC中的廣泛應用[19,29,30], 2002年Strecker等[31]和 Khaykovich等[32]科學家利用Feshbach共振技術調節原子間的相互作用從排斥到吸引, 首次在7Li原子BEC系統中實驗觀察到亮孤子.之后 Cornish等[33]同樣利用Feshbach共振技術, 在超冷85Rb原子BEC系統中實驗觀察到亮孤子.

在BEC系統中, 一般認為一維孤子是可以穩定存在的, 而二維及以上系統的孤子卻很難穩定.隨著一維孤子在BEC中的實驗實現[27,28,31,32],BEC中高維孤子的產生、穩定性及其衰變動力學成為當前科學家關注的熱點和難點問題[34].以暗孤子為例, 在BEC中產生物質波暗孤子需要具備如下幾個特點: 首先在原子背景上具有局部的密度最小值, 而且在局部密度最小值處波函數的相位有一個突變, 與此同時局域密度最小值的幅度和形狀不發生改變[28,35].研究發現暗孤子兩側的相位對暗孤子的速度和深度起了決定性作用[36].特別地, 當暗孤子兩側的相位差為 π 時, 暗孤子的深度為 1 00% ,即孤子中心處沒有粒子, 我們稱之為全暗孤子或黑孤子.此時孤子的速度為零.暗孤子的這一特點以及BEC中原子分布的不均勻性, 使得在二維BEC系統中, 條紋暗孤子很不穩定, 極易受到橫向擾動的影響, 表現出蛇形(snake)不穩定性[37,38],最終衰變為渦旋對[39].Dutton等[40]利用慢光技術 (slow light technique)在 BEC中引入密度缺陷, 在密度缺陷的衰變過程中產生了條紋暗孤子.他們進一步觀察到條紋暗孤子的蛇形不穩定性, 以及從條紋暗孤子衰變成渦旋的動力學過程.在三維BEC系統中, Anderson等[41]發現條紋暗孤子更加不穩定, 會很快衰變成各種渦旋環結構.

隨著對暗孤子性質理解的不斷深入[42], 人們逐漸認識到在二維非線性均勻系統中, 條紋暗孤子的不穩定性區域是由最大擾動波數Qmax表征的[43].當條紋暗孤子的長度L<2π/Qmax時, 條紋暗孤子的不穩定性會被抑制[44].此時直的條紋暗孤子會發生彎曲, 進而閉合成可以長時間穩定存在的環狀暗孤子.環狀暗孤子最早是在非線性光學系統中理論預言[45,46]和實驗實現的[47,48].在非線性光學系統中, 環狀暗孤子可以用于全光控制、光學開關以及塊體介質中光學信息傳輸通道的多路復用與分解[47].由于環狀暗孤子比一般的孤子如條紋暗孤子、塊狀(lump)暗孤子等具有更好的穩定性和更豐富的動力學性質, 因而引起了冷原子物理學家的關注[24,44,49?51].Theocharis等[44]最早在 BEC 中引入了環暗孤子的概念, 并討論了BEC中環狀暗孤子的解析解、穩定性以及動力學性質.他們發現由于環狀暗孤子特殊的對稱性質, 使得即使在諧振子外勢下, 密度不均勻的BEC系統中, 環狀暗孤子在某些條件下仍然可以較長時間穩定存在.環狀暗孤子可用于產生量子湍流, 進而理解量子湍流的統計性質及其內在的物理機理[52?54].利用環狀暗孤子衰變可以產生各種類型的渦旋結構和斑圖, 從而為深入研究渦旋動力學和斑圖動力學等各類非線性現象提供新的技術手段和思路.在負質量流體[55]、人造規范系統[21,56]、SU(3)自旋軌道耦合[57]等特殊量子體系中研究環狀暗孤子的性質, 還有望發現新的量子流體動力學規律, 為設計各種新的拓撲功能材料提供理論依據.因此, 在量子流體系統中研究環狀暗孤子的基本性質和動力學行為具有非常重要的意義.

本文旨在結合BEC和孤子研究的現狀, 綜述BEC中環狀暗孤子的解析解、穩定性操控及其衰變動力學等方面的相關研究進展.第二部分針對BEC原子一般束縛在諧振子勢阱中, 從而使得系統具有密度分布不均勻這一完全不同于非線性光學均勻系統的特點, 首先介紹了一種處理諧振子束縛系統中精確環狀暗孤子解的變換方法, 然后將該方法推廣到原子間相互作用隨時間變化的系統.這一工作進一步建立了非均勻的BEC系統跟均勻的非線性光學系統之間的密切聯系, 為孤子問題的解析分析開辟了新的道路.第三部分致力于討論BEC系統中環狀暗孤子的穩定性.鑒于先前研究中僅討論了橫向擾動對環狀暗孤子的影響, 考慮到實際的實驗情況, 重點討論了環狀暗孤子形狀的微小形變對環狀暗孤子穩定性的影響.通過數值模擬計算, 得到了環狀暗孤子關于橢圓偏心率和深度的穩定性相圖.結果表明較淺的孤子可以以較大的偏心率穩定存在.我們還將亮孤子研究中廣泛應用的Feshbach共振技術, 引入到環狀暗孤子的穩定性操控.理論預言利用Feshbach共振技術周期性調節BEC原子間的相互作用, 可以在同等條件下極大地延長環狀暗孤子的壽命.環暗孤子除了可以在一定程度上克服條紋暗孤子遭遇的蛇形不穩定性之外, 還在其不穩定區域表現出豐富的衰變動力學.第四部分將討論BEC系統中環狀暗孤子衰變為渦旋對以及渦旋在諧振子束縛的BEC系統中的運動規律, 還將說明利用環狀暗孤子衰變引起的自發對稱性破缺, 通過周期性調節原子間的相互作用可以在BEC產生各種斑圖結構.最后對BEC中環狀暗孤子的相關研究進行了簡單的總結和展望.

2 相互作用可調的BEC中環狀暗孤子的解析解

一般來說, BEC系統中的相互作用是不隨時間和空間變化的.但隨著Feshbach共振技術的發展, 科學家已經可以對BEC系統中的相互作用強度甚至正負進行調節.目前為止, 科學家已經相繼發現了磁Feshbach共振[29,30]、光Feshbach共振[58,59]、束縛誘導的共振[60,61]以及軌道Feshbach共振[62,63]等.這些類型的Feshbach共振技術為調節BEC中的相互作用提供了有力工具.利用Feshbach共振相關技術, 科學家已經理論預言和實驗實現了各種隨時間[31,64?66]和空間[67,68]變化的原子間相互作用.因而, 在BEC系統中研究相互作用隨時間變化的孤子解具有重要的現實意義.

二維諧振子外勢中相互作用隨時間變化的BEC的運動規律可由如下非線性薛定諤方程描述[51]

跟一般的非線性光學系統相比, 求解BEC中環狀暗孤子解的一個困難是諧振子外勢的存在.當沒有諧振子外勢即?=0 時, 根據環狀暗孤子的對稱性,系統可以表示為如下形式:

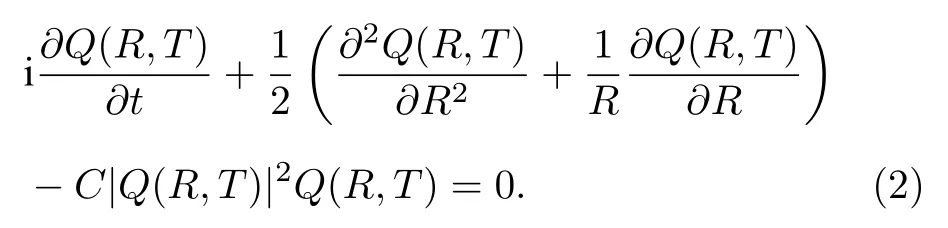
利用微擾方法在小振幅近似下, 方程(2)可以變換到著名的CKdV方程[45,46].利用CKdV方程的解析解[69?74], 可以間接得出方程(2)的環狀暗孤子解析解.當存在諧振子外勢即?0 時, Theocharis等[44]討論了相互作用為常數時, 系統可能存在的環狀暗孤子解.

下面介紹一套變換方法來求解相互作用隨時間變化的BEC系統的環狀暗孤子解析解[51].首先,將方程(1)做如下變換:

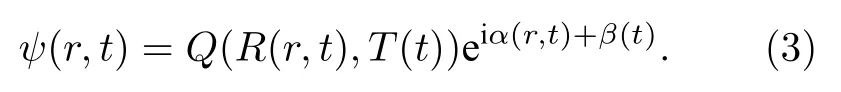
假設R(r,t) ,T(t) ,α(r,t) 和β(t) 為實函數, 并且滿足

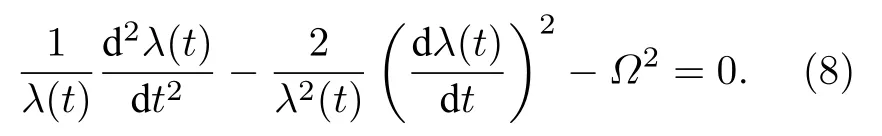
在該變換下方程(2)的所有解析解都可以轉化為方程(1)的解析解.這就在非線性光學均勻系統和非均勻BEC系統之間建立了一個橋梁.利用這一變換關系, 在其中一個系統中得到的相關結果, 都可以在另一個系統中找到對應, 從而為研究非線性光學和BEC動力學提供新的思路.

該變換方法還可以推廣到更為一般形式的非線性薛定諤方程[51]

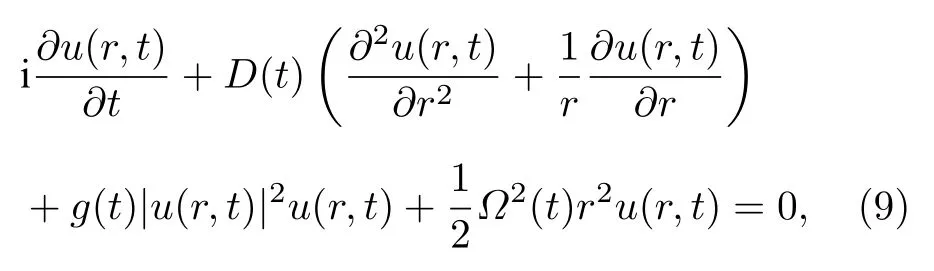
其中需滿足g(t)∝D(t) .對于BEC系統來說, 因為D(t) 為常數, 所以此時相互作用也必須為常數.因而方程(9)轉化為諧振子外勢束縛強度隨時間變化的情形

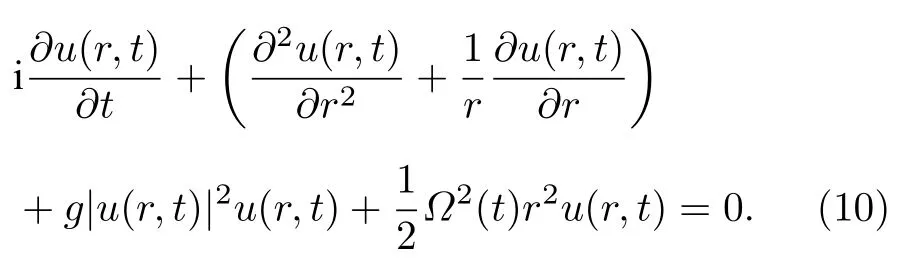
利用方程(10), 可以求解諧振子束縛強度隨時間變化的BEC系統的環狀暗孤子解析解.

需要特別強調的是, 該解析方法只是在小振幅近似下才能成立.所以對應于BEC系統, 就要求得到的環狀暗孤子深度不能太深.對于深的環狀暗孤子, 目前尚無有效的解析處理方法, 需要借助數值模擬計算, 直接求解原始的非線性薛定諤方程(1).

3 BEC中環狀暗孤子的穩定性

3.1 環狀暗孤子在形變擾動下的穩定性相圖

環狀暗孤子的穩定性首先受到橫向擾動的影響, 表現出蛇形不穩定.Theocharis等[44]率先研究了橫向擾動對BEC中環狀暗孤子穩定性的影響,指出淺的環狀暗孤子可以不受蛇形不穩定影響而長時間穩定存在, 而深的環狀暗孤子將遭受蛇形不穩定而衰變成環狀分布的渦旋陣列.考慮到真實的實驗情況, 除了橫向擾動之外, 環狀暗孤子還有可能受到包括徑向擾動在內的更為復雜形式的外部擾動.下面重點討論形變擾動對環狀暗孤子穩定性的影響.

環狀暗孤子在形變擾動下的穩定性可以通過數值求解非線性薛定諤方程(1)來進行分析[51].首先選擇如下形式的環狀暗孤子解

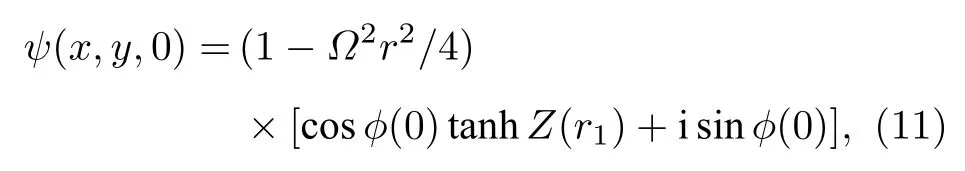
3.2 基于Feshbach共振的環狀暗孤子穩定性操控

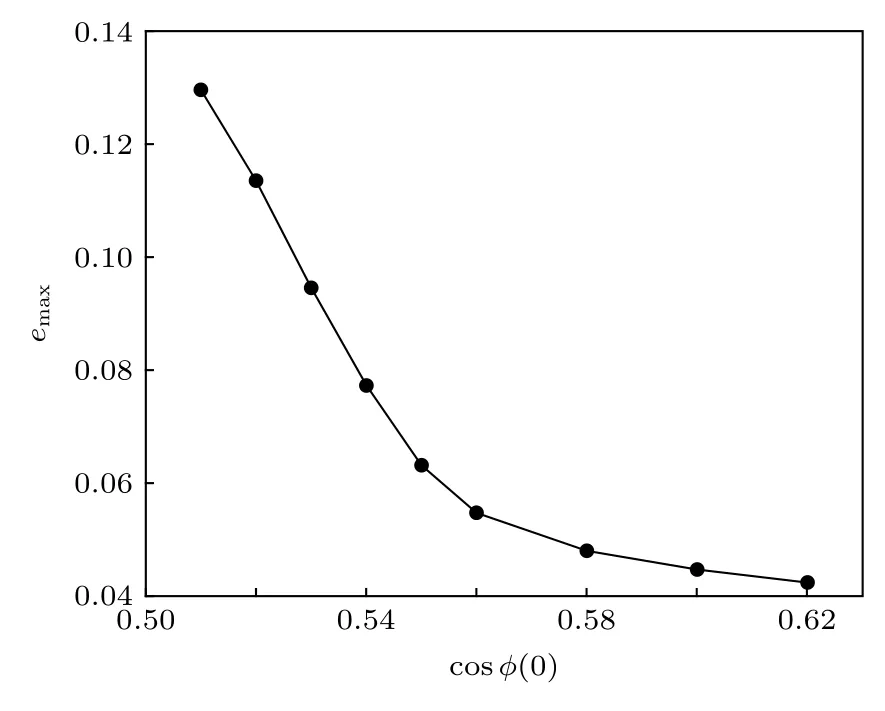
圖1 形變擾動下環狀暗孤子的穩定性相圖[51]Fig.1.Stability phase diagram of ring dark solitons under deformation perturbation.

Feshbach共振技術在BEC孤子研究中扮演了重要的角色.實驗上利用Feshbach技術不但可以產生孤子[31?33], 而且還可以用來調控孤子的穩定性[75].最近, 利用Feshbach共振隨時間周期性改變原子間的相互作用引起了理論和實驗學家的極大興趣[65,76?80].Saito 和 Ueda[78]以及 Abdullaev等[79]發現利用Feshbach共振調節原子間相互作用在吸引和排斥之間的快速振蕩, 可以在二維空間維持穩定的物質波亮孤子.Liang等[80]進一步研究了在周期調控的原子間相互作用下, 物質波亮孤子跟背景之間的原子數目交換規律.本節將從理論上討論如何利用Feshbach共振技術增強環狀暗孤子的穩定性.

假設隨時間周期性振蕩的相互作用具有如下形式

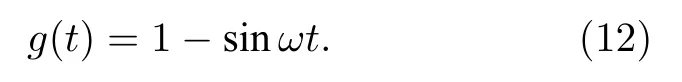
方程(12)表明原子間的排斥相互作用強度在0?2之間周期性振蕩.計算結果表明[51]在某一振蕩頻率附近, 環狀暗孤子的穩定性明顯增強.即使對于較深的暗孤子, 在相互作用處于該振蕩頻率下, 仍然可以具有很長的壽命.以環狀暗孤子深度cos?(0)=0.76為例, 通過上一節的討論, 我們知道環狀暗孤子在此深度下是極不穩定的.通過數值模擬計算,得到了環暗孤子壽命隨相互作用振蕩頻率的變化情況, 如表1所列.可以發現, 當相互作用振蕩頻率在諧振子固有頻率?附近時, 環暗孤子的壽命急劇增長; 當相互作用的振蕩頻率遠離該固有頻率時, 環狀暗孤子的壽命迅速減小.這說明環狀暗孤子壽命的增長是由于相互作用的振蕩頻率跟諧振子的振蕩頻率發生共振引起的.

表1 環狀暗孤子壽命隨相互作用振蕩頻率的變化[51]Table 1.Life of the ring dark soliton as a function of the interaction oscillation frequency.

我們還發現當相互作用振蕩頻率處于該諧振子振蕩頻率時, 較淺的環狀暗孤子即使發生了很大的形變, 仍然可以長時間穩定存在.例如, 計算了環狀暗孤子深度為 cos?(0)=0.6 , 形變引起的偏心率ec=0.4 時環狀暗孤子的壽命.計算結果表明, 當相互作用為常數即g=1 時, 環狀暗孤子的壽命小于 1 0ms .而當相互作用以頻率?在g=1 附近振蕩, 即g=1?sin?t時, 環狀暗孤子的壽命可以長達 5 0ms .

4 環狀暗孤子衰變動力學

當環狀暗孤子處于不穩定區域時, 通常會在遭遇蛇形不穩定下發生衰變[39,44], 導致各種類型和數目的渦旋極子或者不同樣式的斑圖.從而建立了BEC中孤子和渦旋以及斑圖[81]等非線性現象之間的密切聯系.研究BEC中環狀暗孤子衰變引起的各種渦旋動力學和斑圖形成有助于理解量子湍流[52,82,83]和各類相關非線性現象的物理機理.

4.1 環狀暗孤子衰變與渦旋動力學

4.1.1 單分量BEC中的環狀暗孤子衰變與渦旋動力學

Theocharis等[44]最早研究了單分量BEC中環狀暗孤子的衰變動力學.他們發現較深的環狀暗孤子在橫向擾動下將衰變為由渦旋-反渦旋對構成的環形分布的渦旋鏈.越深的環狀暗孤子將衰變出更多的渦旋.渦旋-反渦旋對的數目滿足某種規律,即總是4的倍數, 并且長時間演化后部分渦旋湮滅, 最后只剩下4個渦旋-反渦旋對可以長時間穩定存在.與此同時, 環暗孤子在BEC中衰變產生的渦旋團簇不是固定不動的, 而是以某種規律做周期性運動.運動的形式依賴于渦旋的個數和系統的對稱性質.

接下來重點討論在形變擾動下, 環狀暗孤子的衰變動力學.同樣選擇環狀暗孤子解(11)式作為初始態代入方程(1)進行演化.特別地, 假設環狀暗孤子的深度為 cos?(0)=0.6 , 相互作用強度和諧振子束縛頻率固定在g=1 ,?=0.028 , 發生形變的偏心率為ec=0.4 .前邊的結果已經表明當不發生形變時, 深度為 0 .6 的環狀暗孤子是相對穩定的,因而接下來觀察到的孤子衰變主要是由形變引起的.數值模擬計算指出[51], 在環狀暗孤子發生形變時的衰變行為跟不發生形變時的衰變行為具有明顯的不同.在橢圓形變影響下, 環狀暗孤子衰變產生的渦旋-反渦旋對的數目不再是4的倍數, 或2 的偶數倍, 而是 2 的奇數倍, 如圖2所示.這可以從橢圓形變擾動打破了系統的旋轉對稱性來理解.渦旋個數的不同引起了不同的渦旋運動規律.對于圖2所示的兩個渦旋對的情況, 可以看到每個渦旋分別在 1 /4 圓周的扇形軌跡上做周期性運動.而對于四個渦旋對的情況, 每個渦旋分別在 1 /8 圓周的扇形軌跡上做周期性運動[44].

環狀暗孤子在形變擾動下的詳細衰變動力學過程為[51]: 首先環狀暗孤子沿著徑向收縮到一個最小半徑Rmin, 然后在蛇形不穩定性作用下迅速衰變為兩個暗塊孤子; 這兩個暗塊孤子隨后沿著相反的方向遠離BEC中心移動, 并隨著背景原子數密度的減小而劈裂為兩個渦旋極子, 渦旋極子繼續向前運動; 當渦旋極子到達凝聚體邊界時, 正負渦旋分開并以相反的方向沿著凝聚體邊界做近似圓周運動; 當旋轉90°角后, 來自不同渦旋極子的渦旋相遇, 并重新組合成新的渦旋極子, 然后朝著BEC中心運動.隨著背景原子數密度的增大, 渦旋極子中的渦旋間距逐漸減小, 重新融合成暗塊孤子, 并試圖恢復原來的環狀暗孤子狀態; 當到達Rmin附近時, 兩個暗塊速度降為0, 然后按照原來的路徑返回, 并周期性地沿著四個扇形邊界做往復運動.值得注意的是, 在返回途中由于運動方向相反, 暗塊分裂成的渦旋極子中的兩個渦旋的旋轉方向也同時發生了反轉.此外, 環狀暗孤子衰變形成的兩個渦旋極子的運動跟渦旋四極子在BEC中的運動規律有些類似[84].

圖2 單分量BEC中形變擾動下環狀暗孤子的衰變行為[51]Fig.2.Decay of the ring dark soliton under deformation perturbation in a single-component BEC.

4.1.2 兩分量BEC中的環狀暗孤子衰變與渦旋動力學

當BEC中的原子處于兩個超精細能級時, 系統是由兩個非線性薛定諤方程耦合的方程組來描述的, 一般具有如下形式:

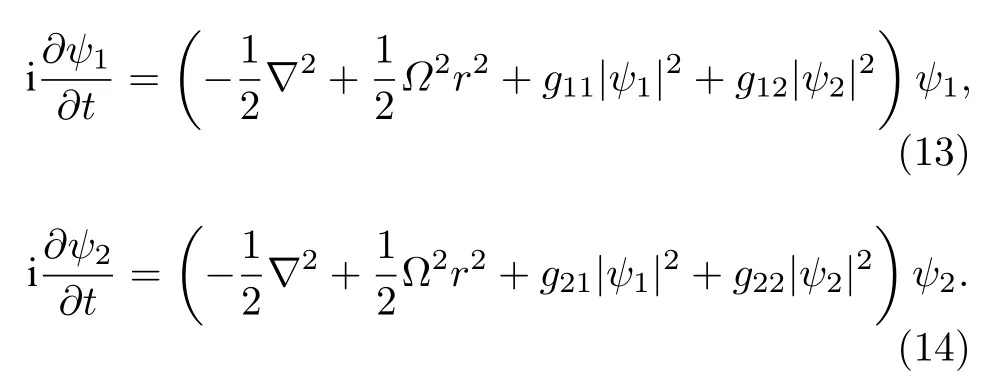
在兩分量系統中, 孤子的運動表現為兩種模式, 類似于非線性光學中處于不同模式的矢量孤子[2].由于不同分量原子之間的相互碰撞, 使得處于不同分量的孤子可以相互耦合, 表現為更為豐富的非線性動力學性質[85].

假設處于兩個不同分量的環狀暗孤子在初始時刻具有如下形式

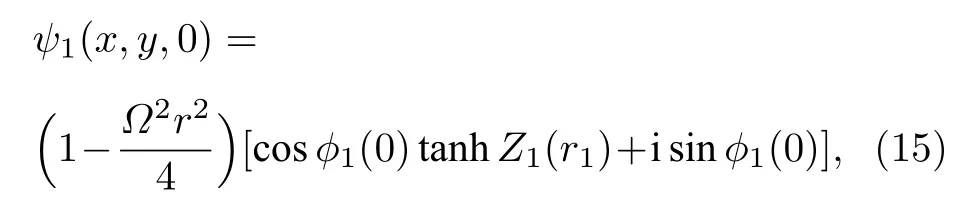
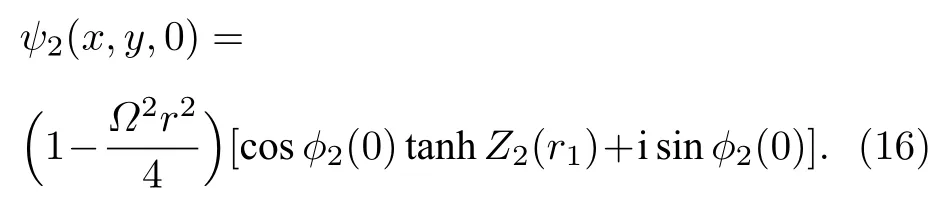
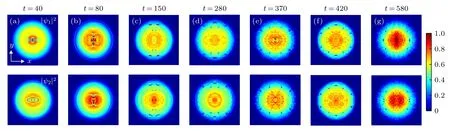
圖3 兩分量BEC中相同深度環狀暗孤子的衰變行為[86]Fig.3.Decay of the ring dark solitons with the same depth in two-component BECs.

圖4 四組渦旋極子在兩分量BEC中的動力學演化[86]Fig.4.Evolution of four vortex dipoles in two-component BECs.

當將初始環狀暗孤子的深度增大為cos?1(0)=cos?2(0)=0.75時, 系統表現出完全不同的環狀暗孤子衰變動力學[86], 如圖3 和圖4 所示.首先, 由于深度的增加, 環狀暗孤子衰變生成了更多數目的渦旋極子.由圖3(b)可以看到共產生了6對渦旋極子, 這跟前邊單分量系統中提到的橢圓形變下,環狀暗孤子衰變成渦旋極子的個數總是2的奇數倍的結論一致.這些渦旋極子產生后, 分為兩組(每組三對)分別沿著相反的方向朝BEC邊界上運動; 在運動的同時同一組的渦旋極子之間逐漸散開, 形成一種三角結構, 如圖3(c)所示; 之后靠近邊緣的兩對渦旋極子分別貢獻一個渦旋而重組成一個新的渦旋極子; 新組的渦旋極子沿著BEC中心運動, 當到達最小半徑Rmin處后原路返回, 并在到達BEC邊界后很快湮滅.剩下的4對渦旋極子可以在BEC中保持非常的壽命, 并以某種規律做周期性運動, 如圖4所示.

當沒有形變擾動時, 盡管開始的環狀暗孤子衰變可能產生很多的渦旋極子(4的整數倍), 但最終只剩4對渦旋極子可以長時間穩定存在[44].當存在形變擾動時, 環狀暗孤子衰變最終生成的4對渦旋極子, 表現出跟沒有形變擾動時完全不同的運動規律.當沒有形變擾動時, 四對渦旋極子的運動是同步的, 四組渦旋極子會在同一時刻發生重組, 并且每個渦旋都沿著 1 /8 的扇形邊界做周期性往復運動[44].當存在形變擾動時, 四對渦旋極子分為運動不同步的兩組, 當其中一組發生重組時, 另外一組尚未發生重組, 兩組渦旋極子中的渦旋以相同的規律分別沿著 1 /4 圓的扇形邊界做周期性往復運動,如圖4所示.

當兩分量BEC中的環狀暗孤子具有不相等的初始深度時, 例如假設 cos?1(0)=0.6 , cos?2(0)=0.75, 根據經驗我們期待較深的環狀暗孤子將衰變出更多數目的渦旋.事實上, 在環狀暗孤子發生衰變的初期確實觀察到了兩個組分中環狀暗孤子不同的衰變行為, 如圖5(b)所示.但由于兩個組分之間的耦合作用, 較深的環狀暗孤子衰變成渦旋的數目被抑制, 最終導致衰變產生的渦旋數目跟cos?1(0)=cos?2(0)=0.6時相同, 如圖5(c)所示.由于初始衰變行為的不同, 本來兩個分量的渦旋運動應該是不同步的, 但數值模擬結果顯示, 兩個分量的渦旋會在產生后很短的時間內趨于同步, 如圖5(c)—圖5(g)所示, 這可以理解為兩分量之間原子相互碰撞耦合的結果.

兩分量BEC中環狀暗孤子衰變成渦旋后的動力學行為跟單分量情況相比還有一個明顯的不同是渦旋在沿著扇形軌跡運動的同時, 還伴隨著進動現象[86,87].這是由于來自兩個分量的渦旋一般是不相互重合的, 一個分量的渦旋核總是被另一個分量的原子填充, 形成所謂的半量子化渦旋[20,88].由于在同一位置附近, 來自兩個分量的渦旋具有相同的旋轉方向, 在分量間原子的碰撞耦合作用下, 它們將繞著兩個渦旋的中間位置(即質心處)沿渦旋自轉的同一方向作進動.

圖5 兩分量BEC中不同深度環狀暗孤子的衰變行為[86]Fig.5.Decay of the ring dark solitons with different depths in two-component BECs.

4.2 環狀暗孤子衰變與斑圖形成

斑圖(pattern)是指空間上具有某種規律性的非均勻分布.在自然界中, 雖然不同系統所顯示的斑圖結構無論從時空尺度還是從形成機制等方面都各不相同, 但他們在形態上都有一定的相似性.斑圖動力學就是研究自然界中千變萬化的斑圖結構的生長與形成、競爭與選擇、漸變與突變等的共性規律.斑圖動力學作為非線性科學的一個重要研究方向[81], 目前已經深入到非常廣泛的研究領域,例如光學[89]、流體力學[90]、等離子體物理[91]以及材料科學[92]等.BEC作為一種非線性多體系統,為研究斑圖動力學提供了高度可控的優越平臺[93].

可以借助環狀暗孤子衰變引起的自發對稱性破缺, 通過周期性調控系統的非線性強度, 來實現各種有規律的斑圖結構.考慮兩分量的BEC, 并假設可以通過Feshbach共振等技術周期性調控原子間的相互作用.特別地, 固定組分內部的相互作用強度, 而周期性地改變組分之間的相互作用強度.此時, 非線性薛定諤方程組(13)式和(14)式中的非線性系數可表示為g11=g22= 1,g12=g21=1?sinωt.考慮方程(15)式和(16)式描述的環狀暗孤子, 并假設偏心率ec=0 .當諧振子頻率?=0.028, 相互作用的周期調制頻率跟諧振子發生共振, 即ω=?, 初始時刻環狀暗孤子深度cos?1(0)=cos?2(0)=1, 半徑為R10=27.9 和R20=28.9時, 環狀暗孤子的衰變行為如圖6和圖7所示[94].

最初環狀暗孤子沿著徑向做周期性振蕩, 并誘導了大量較淺的環狀暗孤子.隨著時間的演化,BEC邊緣的環狀暗孤子首先遭受蛇形不穩定, 衰變為八角形結構, 如圖6(d)所示.這種環狀暗孤子的不穩定性逐漸從BEC邊緣進入到BEC內部,最終在整個BEC中形成了隨時間不斷變化的斑圖結構, 如圖6(e)、圖6(f)和圖7所示.

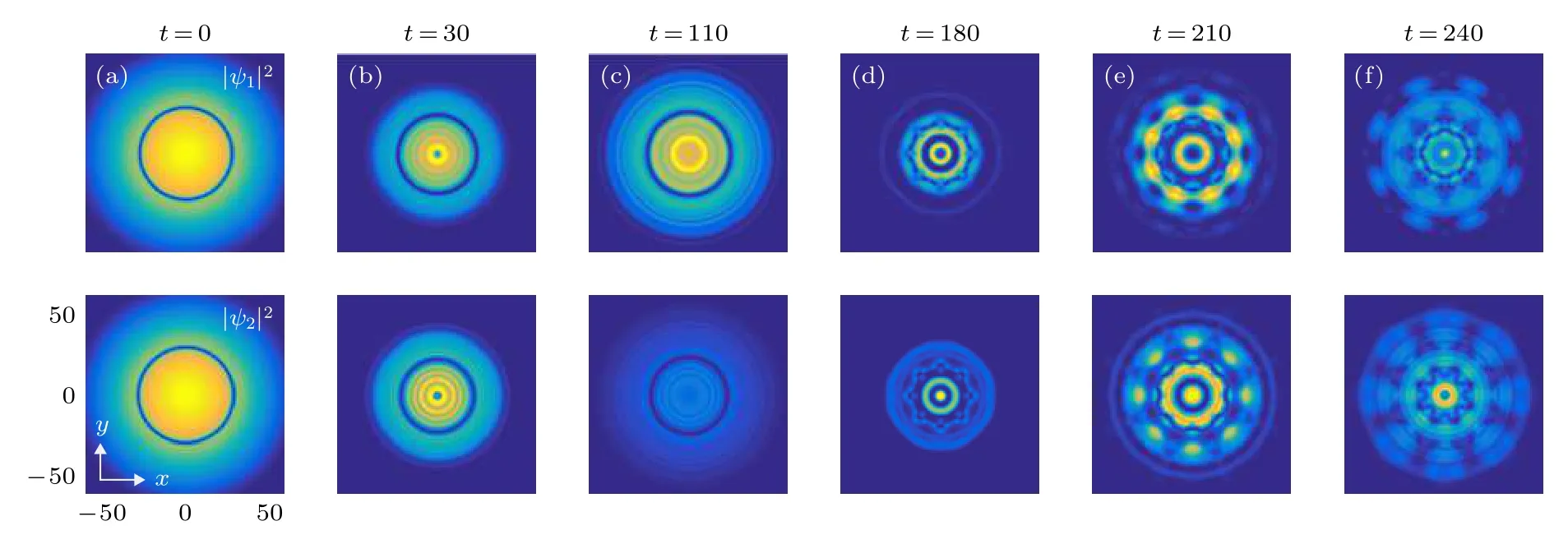
圖6 周期調制相互作用系統中環狀暗孤子衰變引起的斑圖形成[94]Fig.6.Pattern formation induced by the decay of ring dark solitons in a system with periodically modulated interactions.

圖7 斑圖在周期調制相互作用系統中的演化[94]Fig.7.Evolution of the pattern in a system with periodically modulated interactions.

在兩分量BEC中, 兩分量的原子是相分離還是相混合一般由原子間相互作用強度決定[95?98].對于不隨時間變化的原子間相互作用, 當g11g22時, 系統表現為相分離, 此時兩分量中的原子密度分布在空間上是相互填充的.當前考慮的系統相互作用g12是在0—2之間隨時間周期性變化的, 既不滿足又不滿足數值模擬結果表明: 在該條件下系統傾向于相分離, 兩個分量的原子相互在對方的低密度區域填充, 如圖6(d)—圖6(f)和圖7所示.

需要特別強調的是, 斑圖的形成跟系統的對稱性破缺有密切聯系.圖6和圖7中斑圖的形成依賴于環狀暗孤子的自發旋轉對稱性破缺.但是單純依靠環狀暗孤子的自發破缺只能得到有限數目的渦旋極子, 并不能得到斑圖結構.周期調制的非線性在斑圖形成過程中同樣扮演了重要角色.此外, 由于BEC具有多參數、高度可控的特點, 利用環狀暗孤子的自發對稱性破缺性質, 結合對BEC其他相關參數的調控, 模擬量子體系中各種樣式的斑圖形成是一個非常有益的工作.

5 總結與展望

環狀暗孤子作為一種非線性激發跟渦旋、斑圖等非線性現象具有密切的聯系, 環狀暗孤子衰變過程中導致的各類渦旋極子動力學以及斑圖形成等正在引起非線性科學研究的廣泛關注.玻色-愛因斯坦凝聚作為一種高度可調控的非線性系統, 為研究環狀暗孤子及其相關動力學提供了優越平臺.最近, 超冷原子玻色-愛因斯坦凝聚領域取得了一些新的理論和實驗進展, 其中包括人造規范勢[56]、自旋軌道耦合[99]、量子液體[100]等.這些進展也正在促進孤子研究的突破[101], 例如理論上已經預言自旋軌道耦合可以用于穩定高維孤子[102,103].人造規范勢尤其是非阿貝爾規范勢在超冷原子氣體中的實驗實現[21], 為研究和發現新的量子流體動力學開辟了道路.在不同規范勢作用下, 環狀暗孤子可能表現出各種新奇的動力學行為.與此同時, 通過設計合適的規范勢來增強環狀暗孤子的穩定性也是一個非常有益的工作.本文討論了環狀暗孤子衰變導致的渦旋及其運動規律, 最近的研究表明自旋軌道耦合也可以在超冷原子系統中誘導出各種豐富的渦旋結構[57,93,104?109].因而在自旋軌道耦合作用下, 環狀暗孤子的衰變行為將發生明顯變化, 可能產生新的渦旋結構和非傳統的渦旋運動規律.量子液體跟量子氣體相比, 一個明顯的不同是原子數密度發生了急劇增大[100].急劇增大的原子數密度可能對環狀暗孤子的穩定性以及衰變動力學產生重要影響.在這些全新的非線性量子多體系統中、借助新的實驗技術研究環狀暗孤子的運動規律、穩定性以及相關的衰變動力學將是一個重要的研究課題.