旋量玻色-愛因斯坦凝聚體拓撲性質的研究進展*

王力 劉靜思 李吉 周曉林 陳向榮 劉超飛 劉伍明

1) (四川大學物理學院, 成都 610065)

2) (北京景山學校朝陽學校, 北京 100012)

3) (太原師范學院物理系, 晉中 030619)

4) (四川師范大學物理與電子工程學院, 成都 610101)

5) (江西理工大學理學院, 贛州 341000)

6) (中國科學院物理研究所, 北京凝聚態物理國家實驗室, 北京 100190)

7) (中國科學院大學物理學院, 北京 100190)

實現玻色-愛因斯坦凝聚的原子大多具備內部自旋自由度, 在光勢阱下原子內部自旋被解凍, 從而使原子可以凝聚到各個超精細量子態上, 形成旋量玻色-愛因斯坦凝聚體.靈活的自旋自由度成為體系相關的動力學變量, 可以使體系出現新奇的拓撲量子態, 如自旋疇壁、渦旋、磁單極子、斯格明子等.本文綜述了旋量玻色-愛因斯坦凝聚的實驗和理論研究, 旋量玻色-愛因斯坦凝聚體中拓撲缺陷的種類, 以及兩分量、三分量玻色-愛因斯坦凝聚體中拓撲缺陷的研究進展.

1 引 言

對于一個多粒子的玻色系統, 當體系的溫度極低, 且原子間的距離足夠靠近時, 大量原子將會凝聚在動量為零的最低能態上, 從而出現一種具有宏觀量子特性的簡并態, 即玻色-愛因斯坦凝聚(Bose-Einstein condensate, BEC)[1?5].當 BEC 被限制在磁勢阱(如四極阱(Paul)[6], Ioffe-Pritvhard阱 (IPT)[7], 時間軌道勢阱 (time orbiting potential,TOP)[8]等)中時, 原子處于弱場束縛態, 內部自旋自由度被凍結, 此時凝聚體性質可以通過標量形式的序參量來描述[9,10].當BEC被限制在光勢阱[11,12]中時, 內部自旋自由度被釋放, 其磁化性質由自旋相互作用決定, 這樣的體系稱為旋量BEC[13?16].

實驗方面, 1998年美國麻省理工學院(MIT)的Stamper-Kurn研究組[16]在沿磁勢阱的中心軸射入紅外線光束形成的光偶極阱中, 首次實現了金屬23Na原子系統的BEC, 通過這一突破性進展把在磁勢阱中凍結的自旋自由度解放出來, 在冷原子物理領域中開辟了旋量BEC研究的嶄新領域.實驗采用光勢阱捕獲和冷卻鈉原子, 當溫度達到1—2 μK, 原子密度數約為 1 × 1014cm–3時, 轉移到磁勢阱中經由射頻誘導蒸發進一步冷卻, 在F= 1,mF= –1 的電子基態上產生含有(5—10) × 106個原子的凝聚體.隨著紅外線激光束能量的提升,在穩定的磁勢阱中控制凝聚體進入光勢阱, 然后關閉磁勢阱, 讓凝聚體處于全光阱中.圖1為光勢阱中F= 1旋量BEC所有精細態上鈉原子的分布,從圖1(b)可以清晰地看到凝聚體分布在三個超精細態上, 金屬鈉原子的自旋自由度被充分釋放.

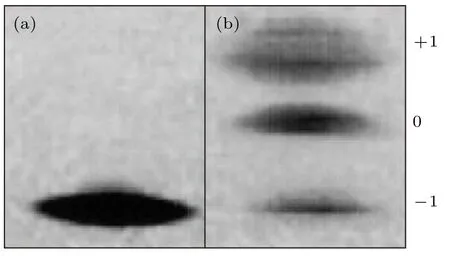
圖1 光勢阱中 F = 1 23Na 凝聚體的超精細態 [16].(a) 250 ms 時光勢阱中鈉原子的吸收圖像; (b) 340 ms時光勢阱中鈉原子的吸收圖像Fig.1.Optical trapping of 23Na condensates in all F =1 hyperfine states: shown are absorption images after(a) 250 ms and (b) 340 ms of optical confinement.

2001年, Barrett等[17]在兩束 CO2激光束 (功率為 12 W, 波長為 10.6 μm)交叉會聚形成的全光阱中得到了F= 1的87Rb原子的旋量BEC.實驗中首先將低速的銣原子裝載到磁光阱中, 接著逐步降低光強, 關閉磁場, 然后把原子抽運到F= 1,mF= 1 態, 最后打開 CO2激光束, 使原子裝載到光勢阱中.整個過程中是通過在2 s時間內逐步降低光強, 即減少阱深來實現蒸發冷卻的.圖2為實驗得到的Stern-Gerlach梯度磁場中自由膨脹10 ms后的原子吸收圖像, 從下到上分別是F= 1,mF=–1, 0, 1 凝聚體的三個分量.

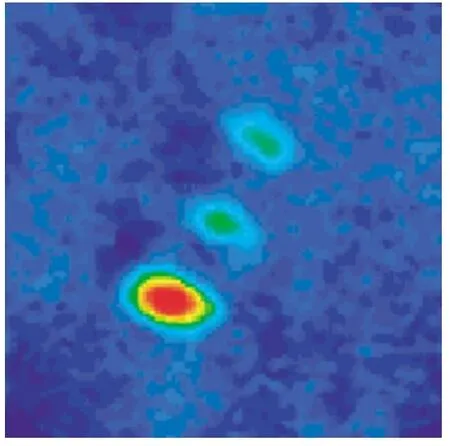
圖2 銣原子云在 Stern-Gerlach 梯度磁場中自由膨脹10 ms后的吸收圖像[17].從下到上分別是 F = 1, mF = (–1,0, 1)凝聚體的三個分量Fig.2.Absorptive image of Rb atomic cloud after 10 ms free expansion in a Stern-Gerlach magnetic field gradient.Three distinct components are observed corresponding to F = 1, mF = (–1, 0, 1) spin projections from bottom to top,respectively.

2003年, Gustavson 等[18]研究了F= 2的23Na旋量BEC, 觀察到了數秒壽命的精細態(F= 2,mF= –2), 且原子密度數為每立方厘米 1014.Chang[19]、Schmaljohann[20]、Kuwamoto[21]等觀察到了F= 2的87Rb旋量BEC, 并研究了其動力學性質.2012年, Pasquiou 等[22]也從實驗上觀察到了F= 3的52Cr旋量BEC, 并研究了其熱力學性質, 表明在極低磁場下, 當自旋自由度被熱激活時,凝聚體的臨界溫度會降低.

特別地, 在2011年, 美國國家標準與技術研究院的Spielman[23]研究組在87Rb旋量BEC中兩個內部自旋態之間通過雙光子拉曼過程實現了等效的自旋-軌道耦合, 這是人類歷史上首次通過人工合成磁場實現了BEC的自旋-軌道耦合效應, 成為近年來冷原子物理中的一個研究熱點[24?27].2012年, 中國科技大學潘建偉[28]研究組也實現了BEC中的一維自旋-軌道耦合.此外, 山西大學[29]和麻省理工[30]的研究組, 分別用40K和6Li實現了費米冷原子氣體中的自旋-軌道耦合.量子氣體中自旋-軌道耦合的實現, 開辟了研究冷原子物理的新方向, 如光與原子相互作用對旋量BEC拓撲結構的影響, 自旋渦旋陣列的產生, 以及各種新奇拓撲缺陷的產生.科研工作者不僅詳細研究了自旋-軌道耦合的BEC的性質[31?34], 還在實驗上成功模擬了Zitterbewegung(狄拉克顫動)[35,36]、自旋霍爾效應[37]等現象, 并提出了研究量子霍爾效應[38]、反常量子自旋霍爾效應[39]、費米氣體中的拓撲量子相變[40]等物理問題的方案.

理論方面, 1998年Ho[41]和Ohmi[42]獨立進行了旋量 BEC的理論研究.他們推廣了Gross-Pitaevskii方程, 在平均場理論下研究了自旋F=1的BEC的基態結構和拓撲缺陷的性質.同年,Law等[43]利用量子光學中的代數方法研究了其自旋混合動力學行為.接著, Koashi[44,45]、Ciobanu[46]和Semenoff[47]等研究了F= 2的旋量BEC的基態結構、自旋相關、磁效應、激發譜及相位等一系列理論性質.Santos[48]、Diener[49]、Makela[50]等對F= 3的旋量 BEC 也進行了理論研究.2007年,Yip[51]研究了自旋F≤ 4的旋量BEC的基態及其對稱性.

BEC作為一種新穎的物質形態, 是物理學前沿的研究熱點之一, 特別是實驗上實現了旋量BEC、分子的BEC、費米凝聚體、自旋-軌道耦合的超冷原子氣體以來, 又掀起了新一輪的研究熱潮.本文綜述了旋量BEC的實驗和理論研究, 旋量BEC中產生的拓撲缺陷的種類, 如自旋疇壁、渦旋、磁單極子、skymions、扭結, 并結合我們的工作著重介紹了兩分量和三分量旋量BEC中拓撲缺陷的研究進展.

2 旋量玻色-愛因斯坦凝聚體

2.1 旋量玻色-愛因斯坦凝聚體的哈密頓量表示

自旋為f的BEC的序參量在旋轉下有2f+ 1個分量, 且這些分量是隨著時間空間變化的, 攜帶關于超流和磁性的信息, 能形成自旋流及質量流,產生豐富的自旋結構[52].

考慮自旋f的全同玻色子體系, 取(r) 為相應的場算符, 假設滿足對易關系:

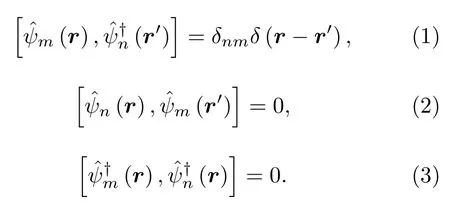
考慮兩個自旋為f的玻色子的耦合作用, 其總自旋F為 0, 2, …, 2f, 耦合態對應的湮滅算符為

哈密頓量具有標量性, 在旋轉下保持不變, 進一步得到相互作用哈密頓量:

其中v(F)(r?r′) 表示相互作用勢, 且

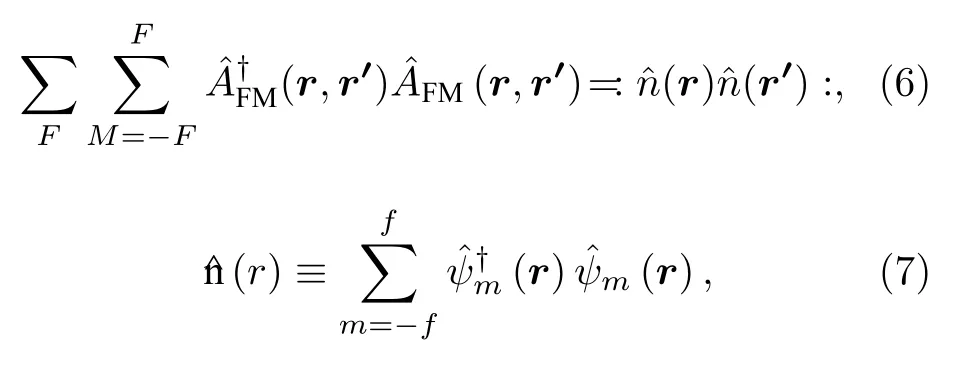
其中gF描述兩個粒子間相互作用強度,aF指S波散射長度.由此哈密頓量可以表示為

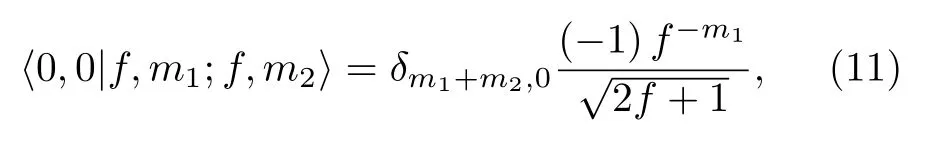
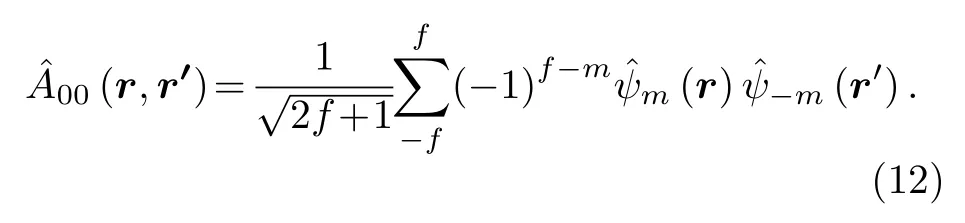
對于自旋f= 1時的相互作用哈密頓量, 此時兩個玻色子碰撞的總自旋F只能是0和2, 相應的相互作用哈密頓量可表示為

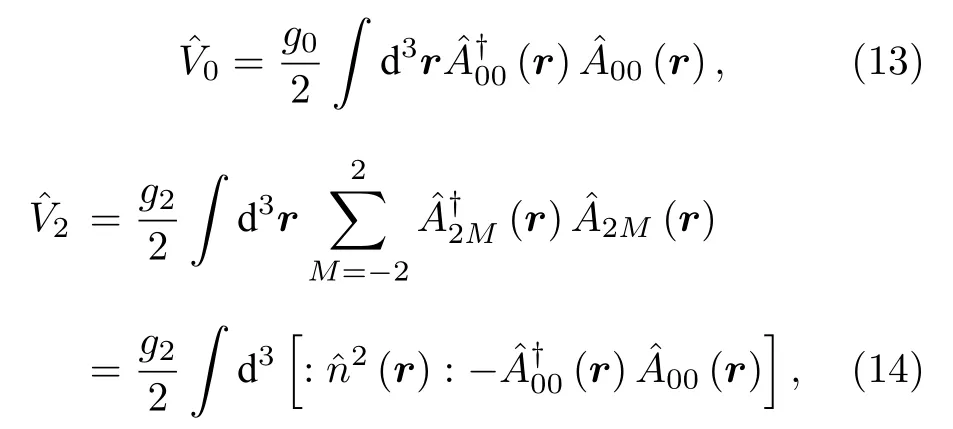
聯合兩式得到總的相互作用哈密頓量為

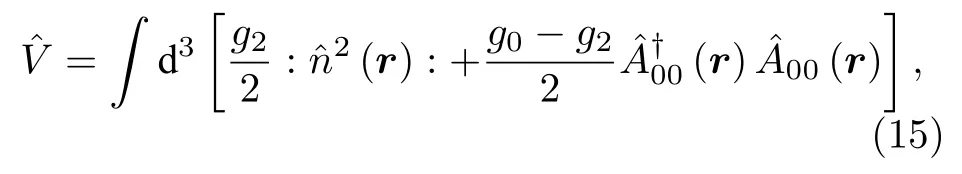
同樣地, 可以得到f= 2 時的相互作用哈密頓量:

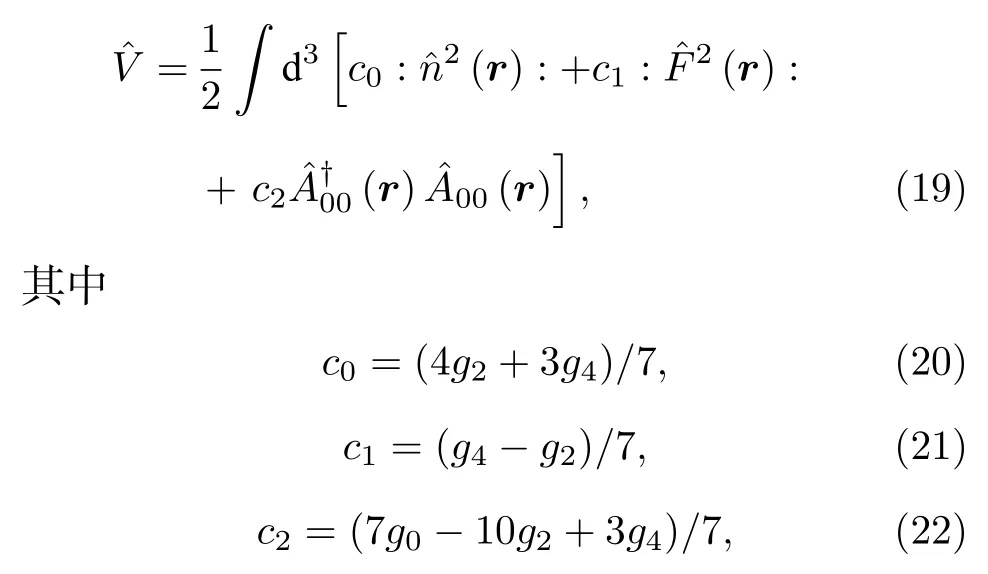
f= 3時的相互作用哈密頓量為

其中

2.2 旋量玻色-愛因斯坦凝聚體的拓撲荷

對于各種形式的拓撲缺陷主要通過計算拓撲荷來判定.線缺陷形式的渦旋可通過觀察相位圖中的奇異點和纏繞數來識別, 對于點缺陷, 如磁單極子, 可以通過計算拓撲荷來確定是整數磁單極子還是分數磁單極子[53].在兩分量BEC系統中, 原子可以是兩種不同的元素[54], 也可以是同種元素的兩種同位素[55], 或者是同種原子的不同超精細態[56],該體系可用贋自旋 1 /2 系統來描述[57,58].

贋自旋S=Ψ?σΨ/|Ψ|2, 其分量形式為

其中y1,y2,q1,q2分別為兩個分量的波函數和相位.局部贋自旋的三個分量可表示為

其中q和j分別為極角和方位角.比較兩式可知贋自旋的極角只與兩分量的相對密度有關, 即贋自旋的Sz分量由兩組分的密度差決定, 而Sx,Sy分量由相對密度和相對相位共同決定, 表明兩分量BEC不同的相對密度和相對相位會導致不同結構的自旋紋理, 可以用拓撲荷密度q(r)來描述其拓撲結構的空間分布:

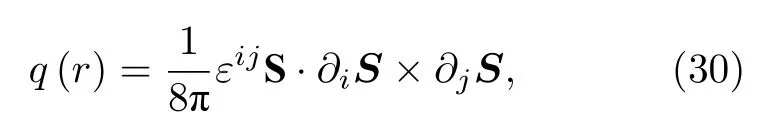
對全空間積分得拓撲荷:

從(31)式可以看出, 任意交換自旋密度矢量的三個分量Sx,Sy,Sz中的兩個分量, 或者任意改變三個分量中其中一個分量的正負號, 將會出現不同結構的自旋紋理, 但其拓撲荷密度q(r)和拓撲荷的絕對值 |Q| 不會變化.

3 拓撲缺陷的分類

拓撲缺陷的獨特性是在弱微擾下能穩定存在,在空間自由連續地變換而不改變其自身性質.這種穩定性由表征序參量流形的離散拓撲量子數保護.拓撲缺陷的分類主要依靠同倫論, 描述不同的拓撲缺陷會出現不同的序參量流形.表1總結了利用同倫群對拓撲缺陷進行分類的結果.旋量BEC有豐富的序參量流形, 因而可產生不同種類的拓撲缺陷, 如整數和分數渦旋[59?64], 非阿貝爾渦旋[65],’ tHooft-Polyakov 磁單極子[66], 狄拉克磁單極子[67?68],skyrmions[69?71]和扭結[72].

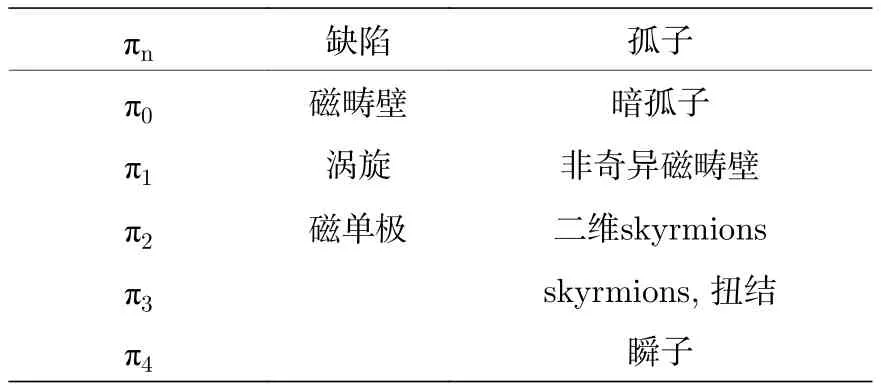
表1 同倫群描述的拓撲缺陷結構Table 1.Topological defect structures described by homotopy groups.

3.1 自旋疇壁

疇壁可由零階同倫群 π0(R) 表 征.若π0(R)=0說明體系是相連的, 若 π0(R)=1 , 說明體系被分為兩個非連續區域.以兩分量贗自旋1/2的序參量來描述, 其贗自旋表示為(28)式.圖3表示在贗自旋表象中自旋密度Sx,Sy,Sz的分布情況.第一組分分布在勢阱的左邊, 標記為自旋朝上Sz=1(圖中紅色表示); 第二組分在強烈的排斥作用下分布在第一組分的低密度區域, 即勢阱的右邊, 標記為自旋朝下Sz= –1(圖中藍色表示).兩個分量的相分離導致在贗自旋表象中形成了兩個自旋疇,在兩個自旋疇的界面上形成了自旋疇壁.在這個區域自旋既不朝上也不朝下(即|Sz|=1 ), 而是在x方向上有了分量.從左邊自旋疇到右邊自旋疇的過程中, 疇壁上的自旋沿著x方向翻轉, 贗自旋在x-y平面的投影均指向x軸的正方向, 形成了如圖3(d)中的經典奈爾型疇壁[73].

3.2 渦 旋

渦旋可由一階同倫群 π1(R) 表征, 描述一個從實空間回路到序參量流形的映射.它屬于線缺陷,常見于超流和液晶位錯中.對于S波超導體、液4He以及旋量BEC, 繞渦旋線的質量環流是量子化的, 其渦旋由纏繞數nw表征:

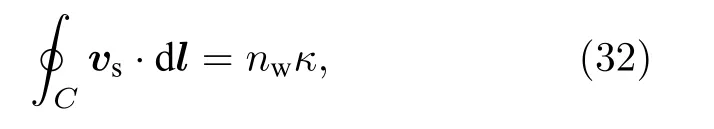
積分沿著閉合路徑C進行, 其中κ≡h/M,vs(= ?/M??)為超流速度.對于標量序參量, 其序參量流形為R=U(1) , 其基本群為整數加群:π1(U(1))～=Z .π1(U(1)) 的群元與纏繞數nw的值是一一對應的[74].

對于自旋 1的鐵磁 BEC, 序參量流形為SO(3), 其基本群為 π1(SO(3))～=Z2={0,1} , 可存在Mermin-Ho渦旋, 對應序參量為:

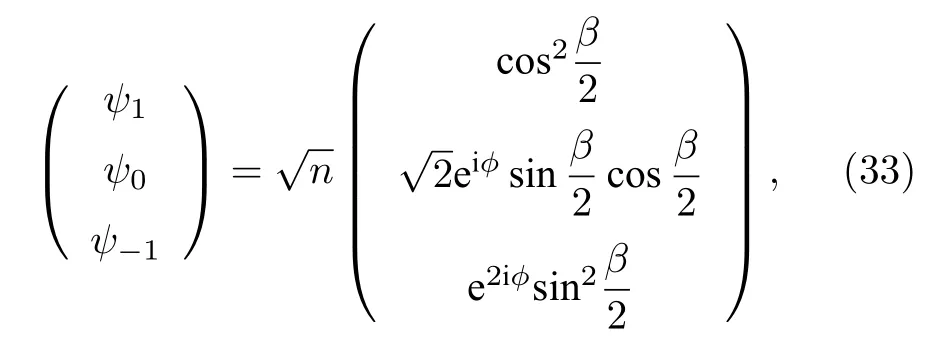
其中b是方位角,?表示極坐標下極角.Mermin-Ho渦旋在中心處的方位角b= 0, 在邊界處對應的方位角β=π/2 .因此, 空間內自旋方向在中心處是垂直的, 邊界處是水平的.這種渦旋的纏繞數組合為 (0, 1, 2), 每個組分的密度分布都是軸對稱的,勢阱中心被y1組分占據,y0組分被推到外部,y–1組分被排擠到最邊緣區域.

圖3 贗自旋密度 Sz, Sx, Sy 的空間分布[73] (a)?(c)表示旋轉角頻率為 0; (d) 自旋紋理投影到 x-y 平面內的矢量表示Fig.3.The pseudospin density distribution for (a) Sz, (b) Sx and (c) Sy for W = 0; (d) the vectorial representation of the spin texture projected onto the x-y plane.

另一種渦旋結構為極核渦旋, 對應序參量為

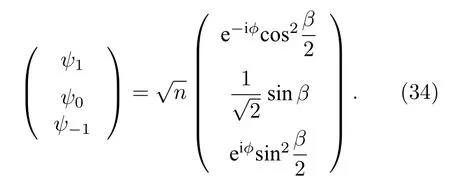
這種渦旋的纏繞數滿足組合 (1, 0, –1).勢阱中心被y0組分占據,y1和y–1組分被推到外部區域.不同于Mermin-Ho渦旋中心處的縱向磁化,極核渦旋代表手征對稱性的自發破缺.

對于渦旋而言, 相位的改變量是量子化的, 應是2π的整數倍[75].在兩分量BEC系統中, 通過光學方法可以實現半量子化渦旋(half-quantized vortice), 描述兩分量系統中, 組分一渦旋的相位改變量是2π, 組分二相位改變量為0的情況.相對于整個系統, 每個組分的相位改變量為π, 因此稱之為半量子化渦旋或 Alice渦旋[76].2017年Liu C F 和 Liu W M[77]利用變分方法, 得到了自旋-軌道耦合和外磁場聯合作用下自旋1BEC中無核半量子渦旋可能的穩定解.計算表明, 各向同性自旋-軌道耦合提供了穩定無核半量子渦旋和相應的奇異半量子自旋紋理激發的局部能量最小.各向同性自旋-軌道耦合和垂直磁場的聯合約束是獲得這種激發的關鍵因素, 研究還提供了半量子渦旋的穩定相圖和最可能的尺寸.圖4為自旋1BEC中半量子渦旋近似解和相應的奇異自旋紋理.在自旋2BEC的單軸向列相和四面體循環相中還存在非阿貝爾渦旋, 其迷向群都是阿貝爾群[78].非阿貝爾渦旋的特點在于其渦旋的生成元是不能互換的, 因此當兩個渦旋碰撞時, 它們不能合并或者通過對方, 而是形成一個rung渦旋粘在一起.

3.3 磁單極子

磁單極子可由二階同倫群 π2(R) 表征, 描述從實空間一個球到序參量流形的映射, 為二維skyrmion結構, 常見的兩種二維skyrmions構型如圖5.在鐵磁BEC系統中可以產生狄拉克磁單極子, 其鐵磁相的序參量為

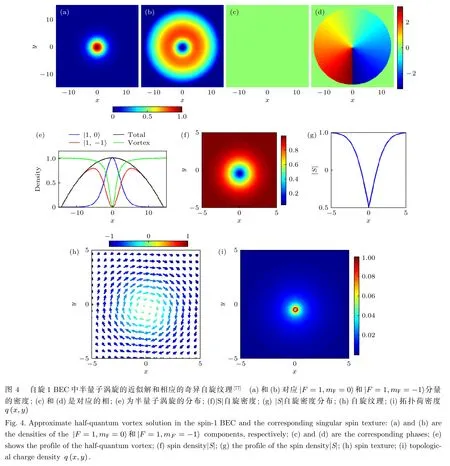
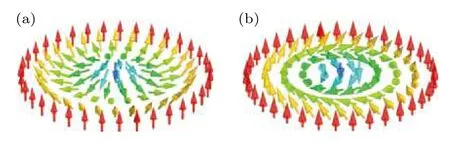
圖5 兩種常見的二維 skyrmions 的矢量場構型[79] (a) 豪豬型 skyrmion; (b) 螺旋型 skyrmionFig.5.Two common vector field configurations of two-dimensional skyrmions: (a) The hedgehog type skyrmion;(b) the spiral type skyrmion.

這樣的點缺陷在鐵磁BEC中三個自旋態的分布分別為: 在y1分量表現為雙量子數渦旋線, 在y0分量表現為單量子數渦旋線, 在y–1分量表現為孤子態, 沒有渦旋線.

自1931年狄拉克磁單極子被首次提出以來,便受到了廣泛關注, 盡管到目前為止仍然沒有探測到真實的磁單極子, 科研工作者在不同領域也取得了較大的進展, 例如固態物理中的自旋冰材料, 便提供了一種人造磁單極子環境.最具有突破性進展的是研究者在鐵磁BEC中實驗上實現了人造磁單極子[80,81].

3.4 三維skyrimion

三維skyrimion可由三階同倫群 π3(R) 表征,這是一個擴展到整個三維實空間的拓撲結構, 類似于粒子的拓撲孤子, 所有自旋有序排列, 在有限空間下自旋會發生反轉.考慮一個鐵磁系統, 對應的序參量具有SO(3) 對稱性.它是在位置r處序參量通過一個向量?表示, 向量的方向和梯度描述了自旋的方向和旋轉的角度.給定條件f(∞) = 0, 保證序參量均勻且在無限遠處等于 zFM= (1, 0, 0)T.給定另一條件f(0) = 2πn保證skyrmion屬于同倫分類.通過酋變換得到序參量表示:

Skyrmion在凝聚態的許多體系中發揮了作用,例如液氦、量子霍爾體系、液晶以及螺旋鐵磁系統,目前在旋量BEC中的skyrimon已經成為研究熱點.圖6是研究者在兩分量BEC中通過非阿貝爾規范場誘導觀察到的三維skyrmions[82,83].

3.5 扭 結

扭結也可由三階同倫群 π3(R) 表征, 表現為一個閉合回路互相嵌套的結構, 描述從三維球空間S3到S2的映射.不同于其他拓撲缺陷, 如渦旋、磁單極子和三維skyrmion通過纏繞數來描述, 扭結是通過連接數或Hopf不變量來描述.Hopf映射是從S3到S2, 在S2中一個點的原像會形成一個無結的回路.假設在BEC系統中給定一個閉合路徑C1, 自旋矢量固定在一個給定的方向, 另一個回路C2沿著自旋不同的方向.如果兩個回路C1和C2連接一次, 那么連接數就為1.連接數可正可負,決定于兩個回路的相對取向.扭結自Faddeev和Niemi提出在三維經典場論中可以穩定孤子的形式存在以來, 引起了物理學家極大的研究興趣.與三維skyrmion的情況一樣,S3域是通過設置一個邊界條件來給定的, 即在空間無窮大的各個方向上, 序參量的值是相同的(.考慮自旋)1的極性相,序參量流形為這里U(1)和 Z2對一維空間以上的同倫群無對稱貢獻, 因此, 得到對應的拓撲荷, 也即 Hopf荷Q∈Z[84].

通過操縱外部磁場, 可以在自旋1BEC中形成扭結.在外部磁場存在時, 線性塞曼效應引起的拉莫爾進動, 而二次塞曼效應往往平行與磁場.假設一個處于光勢阱的 BEC, 其在z方向施加均勻磁場, 然后突然關閉均勻磁場, 打開四極場, 由于線性塞曼效應,開始圍繞磁場旋轉.此時作為時間的函數運動, 從而導致扭結的形成.圖7顯示了四極場作用下球形光勢阱中扭結產生的動力學過程.

圖7 四極場作用下球形光勢阱中扭結產生的動力學過程 [85].上一行表示=(0,0,?1)T 和 = (1, 0, 0)T 的圖像快照, 下一行表示x-y平面上m = –1分量的密度截面Fig.7.Dynamics of the creation of knots in a spherical optical trap under a quadrupole magnetic field.Snapshots of the preimages of = (0, 0, –1)T and = (1, 0, 0)T(top), and the cross sections of the density for the m = –1 components on the x–y plane (bottom).

4 旋量玻色-愛因斯坦凝聚體中的拓撲缺陷研究

4.1 兩分量旋量玻色-愛因斯坦凝聚體中的拓撲缺陷研究

對于兩分量BEC[86], 由于組分內相互作用與組分間相互作用兩者的競爭導致體系出現豐富而有趣的拓撲結構, 如上文介紹的渦旋、skyrmion、磁單極子和量子扭結等, 現已成為實驗研究的理想平臺.實驗方面, 1999年Matthews等[87]在兩分量BEC中產生了量子渦旋.2001年Anderson等[88]采用兩束正交的探測光觀察到雙組分的BEC中暗孤子受動力學不穩定的影響衰變為渦旋環.2016年Hall等[89]演示了在旋量BEC中扭結孤子的實驗創建和檢測, 所觀察到的扭結紋理對應于三階同倫群, 如圖8.

理論方面, 1999年Williams和 Holland[90]展示了在BEC中選擇性地產生具有不同角動量超流渦旋的方法, 包括求解具有強耦合原子態的雙組分凝聚體的時間相關運動方程.2002年Battye等[91]證實了在兩分量BEC中存在穩定的skyrmion結構.同年Martikainen等[92]理論研究了在兩分量BEC中產生磁單極子的方法, 并證明磁單極子的產生并不局限于反鐵磁自旋凝聚, 同時研究了這種磁單極子的膨脹探測, 以及勢阱中位移磁單極子的動力學.2004年Kasamatsu和 Tsubota[93]通過數值積分耦合的Gross-Pitaevskii方程, 研究了雙組分BEC在軸對稱勢阱中由調制不穩定性引起的多疇壁形成動力學.2010年Wang等[94]在無外勢的自旋-軌道耦合兩分量BEC中發現了平面波相和條紋相, 在考慮外勢的情況下, 體系將出現新的量子態, 如分數渦旋和渦旋格子[95]以及skyrmion格子[96].

接著, 人們研究了旋轉勢下自旋-軌道耦合兩分量BEC的基態性質.2011年Xu和Han[97]在旋轉勢下自旋-軌道耦合兩分量BEC體系中發現了對稱排列的渦旋列和中心伴有巨skyrmion的三角渦旋格子.2011年Zhou等[98]探討了具有旋轉和自旋-軌道耦合兩分量BEC的基態性質, 發現了半量子數渦旋格子結構.2012年Liu等[99]總結了skyrmions的類型, 并通過研究自旋-軌道耦合的兩分量BEC的隨機投影Gross-Pitaevskii方程, 發現自旋-軌道耦合能夠誘導系統產生具有兩個Sz極值的環形-雙曲狀的 skyrmions.圖9為總結的skyrmions類型.

圖8 扭結孤子的結構及其產生方法[89] (a)和(b)為扭結形成之前和形成過程中磁感應線的示意圖, 綠色橢圓為對應的凝聚體;(c)和(d)顯示扭結形成時, 最初的z方向的向列相矢量(黑色箭頭)沿著局部磁場(青色線)的方向進動, 以實現最終的結構(彩色箭頭).灰色虛線表示 dz = 0, 白線表示孤子核 (dz = –1), 深灰色線表示體積 V (dz = 1) 的邊界; (e)表示實空間中扭結孤子的構型及其與S2中向列矢量的關系Fig.8.Structure of the knot soliton and the method of its creation: Schematic magnetic field lines before (a) and during (b) the knot formation, with respect to the condensate (green ellipse); (c), (d) as the knot is tied, the initially z-pointing nematic vector(black arrows) precesses about the direction of the local magnetic field (cyan lines) to achieve the final configuration (coloured arrows); the dashed grey line shows where dz = 0, the white line indicates the soliton core (dz = –1), and the dark grey line defines the boundary of the volume V (dz= 1); (e) the knot soliton configuration in real space and its relation to the nematic vector in S2(inset).

2014年Wang等[100]研究了準二維旋轉雙分量BEC在改變自旋-軌道耦合和旋轉頻率強度的情況下呈現出的各種豐富的基態結構, 表明各向異性自旋-軌道耦合引起的不同基態相之間的轉變明顯不同于各向同性的情況.Fetter[101]用時間相關的拉格朗日形式和變分函數研究了自旋-軌道耦合的BEC中雙組分渦旋的動力學.2016年Sakaguchi和Umeda[102]通過數值模擬和變分方法, 研究了Rashba型自旋-軌道耦合的雙組分BEC的Gross-Pitaevskii方程.發現當不存在相互作用時, 多量子渦旋態成為諧波勢中的基態.當引力相互作用較強時, 多量子渦旋態在方位角方向呈現調制不穩定性, 出現孤子態.當排斥相互作用較強時, 形成中心為多量子渦旋的渦旋晶格態, 且渦旋晶格態近似于多量子渦旋態的線性組合.

2017年Sakaguchi[103]通過數值分析研究了雙組分BEC中自旋-軌道耦合條紋和半渦旋物質波孤子在組分間線性混合(Rabi耦合)作用下, 以耦合結構振蕩和穿梭運動形式產生宏觀量子效應的可能性.研究得到在一維系統中, 本征振蕩表現為條紋孤子在空間上的偶數分量和奇數分量之間的翻轉, 而在二維系統中則表現為半渦旋孤子的零渦旋和渦旋分量之間的周期性躍遷.同年, Wang等[104]研究了環形勢阱中自旋-軌道耦合兩分量BEC的旋渦態和自旋紋理, 系統地討論了旋轉、自旋-軌道耦合和原子間相互作用對系統基態渦旋結構和自旋紋理的影響.特別是當旋轉頻率固定在臨界值以上時, 各向同性自旋-軌道耦合的增強使每個分量中有一個可見的渦旋鏈, 在中心區域伴隨著一個隱藏的巨渦旋和一個(或幾個)隱藏的渦旋鏈.Kato等[105]研究了具有Rashba自旋-軌道耦合雙組分BEC中渦旋-反渦旋對的動力學性質, 并且發現旋渦-反渦旋對的速度遠小于無自旋-軌道耦合的速度且存在穩態, 而兩個具有相同環流的渦旋相互移動或聯合會形成一個靜止狀態.

2018年Shi等[106]研究了旋轉非對稱勢阱中具有Dreselhaus自旋-軌道耦合(DSOC)的兩分量BEC中的拓撲缺陷和自旋紋理.結果表明, 對于不含自旋-軌道耦合的初始混合凝聚體, 旋轉頻率的增強可導致系統的結構相變.在各向同性DSOC存在的情況下, 該系統維持渦流對、Anderson-Toulouse無核渦流、圓形渦旋片和組合渦旋結構.特別地, 當旋轉頻率固定在徑向勢阱頻率之上時,強DSOC導致了由多層可見渦旋鏈、隱藏渦旋鏈和隱藏巨渦旋流組成的特殊拓撲結構.Li和Liu[107]利用Gross-Pitaevskii方程研究了自旋-軌道耦合作用和梯度磁場對旋轉兩分量BEC基態的影響.研究結果表明, 在梯度磁場中, 隨著自旋-軌道耦合強度增大, 基態結構由skyrmion格子逐漸過渡為沿著對角線方向排列的skyrmion列.當自旋-軌道耦合強度和旋轉頻率都小的情況, 磁場梯度的增強可導致基態由平面波相轉變為halfskyrmion; 當自旋-軌道耦合強度和旋轉頻率都大的情況, 梯度磁場可誘導hidden渦旋的產生.圖10為不同自旋-軌道耦合強度下梯度磁場中兩分量87RbBEC基態粒子數密度分布和相位分布.

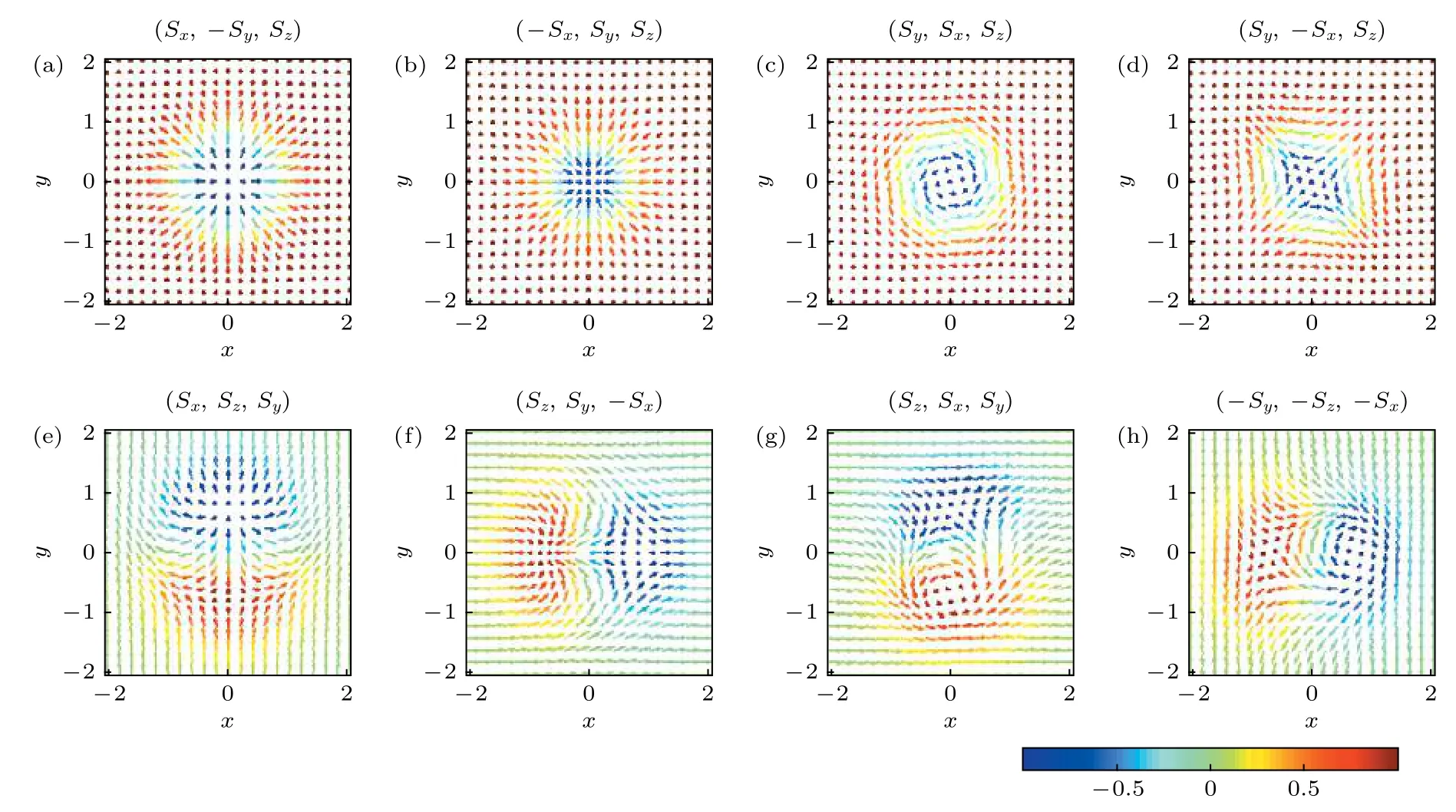
圖9 Skyrmions 的類型 (l = 0.5)[99] (a)?(h)表示自旋矢量的模式: (a)徑向-向外 skyrmion, (b)徑向-向內 skyrmion, (c)環形skyrmion, (d) 雙曲 skyrmion, (e)雙曲-徑向向外 skyrmion, (f)雙曲-徑向向內 skyrmion, (g) 環形-雙曲 skyrmion-I, (h)環形-雙曲skyrmion-IIFig.9.Configuration of the skyrmion where l = 0.5: The (a)?(h) figures indicate the mode of the spin vectors: (a) radial-out skyrmion, (b) radial-in skyrmion, (c) circular skyrmion, (d) hyperbolic skyrmion, (e) hyperbolic-radial(out) skyrmion, (f) hyperbolicradial (in) skyrmion, (g) circular-hyperbolic skyrmion-I, and (h) circular-hyperbolic skyrmion-II[99].

4.2 三分量旋量玻色-愛因斯坦凝聚體中的拓撲缺陷研究

對于自旋F= 1的旋量三分量 BEC, 原子可能占據的塞曼態有三種, 體系內會出現兩種類型基態相——磁相和晶列相, 依賴于自旋無關相互作用和自旋相關相互作用.

實驗上2001年Raghavan等[108]通過靜態直流磁場在三分量旋量BEC中產生了暗孤子和渦旋結構.2002年Ogawa等[109]采用四極磁場將自旋1BEC限制在Ioffe-Pritchard勢阱中, 發現在凝聚體中產生了渦旋.2006年Itin等[110]研究了自旋1BEC在一對載流線和偏置磁場控制的雙磁阱中產生渦旋的幾種機制, 圖11為凝聚體快速分裂過程中渦旋的動力學形成, 顯示動態渦旋存在于凝聚體的所有分量中, 在y–1分量中占 99%以上, 在y0分量中動態渦旋和拓撲渦旋共存.2014年,Ray等[80,81]在自旋1BEC中借助梯度磁場, 觀察到了狄拉克磁單極子, 圖12為狄拉克磁單極子的實驗產生過程, 顯示了凝聚體中不同自旋組分中的粒子密度隨BZ, f的減小而減小.

理論上2002年Isoshima和Machida[111]在旋轉外勢下, 采用推廣的Bogoliubov理論研究了自旋1BEC中各種軸對稱渦旋的穩定結構.同年Mizushima等[112]通過求解廣義Gross-Pitaevskii方程研究了旋轉條件下鐵磁自旋1BEC中的Mermin-Ho 和 Anderson-Toulouse無核渦旋, 得到在鐵磁情況下, Mermin-Ho渦旋是穩定的.2006年Saito等[113,114], 以及 2009年Turner[115]研究了鐵磁自旋1BEC中的極核渦旋, 發現系統核心由mF= 0 原子填充, 圍繞渦旋有mF= 1 分量的質量流, 以及mF= –1分量的相等但自旋相反的質量流, 這就產生了凈自旋流, 但沒有凈質量流.2007年Mottonen等[116]研究了非旋轉條件下在三維拋物勢與Ioffe-Pritchard場中的自旋1鐵磁態旋量BEC中無核渦旋的能量和動力學穩定性.

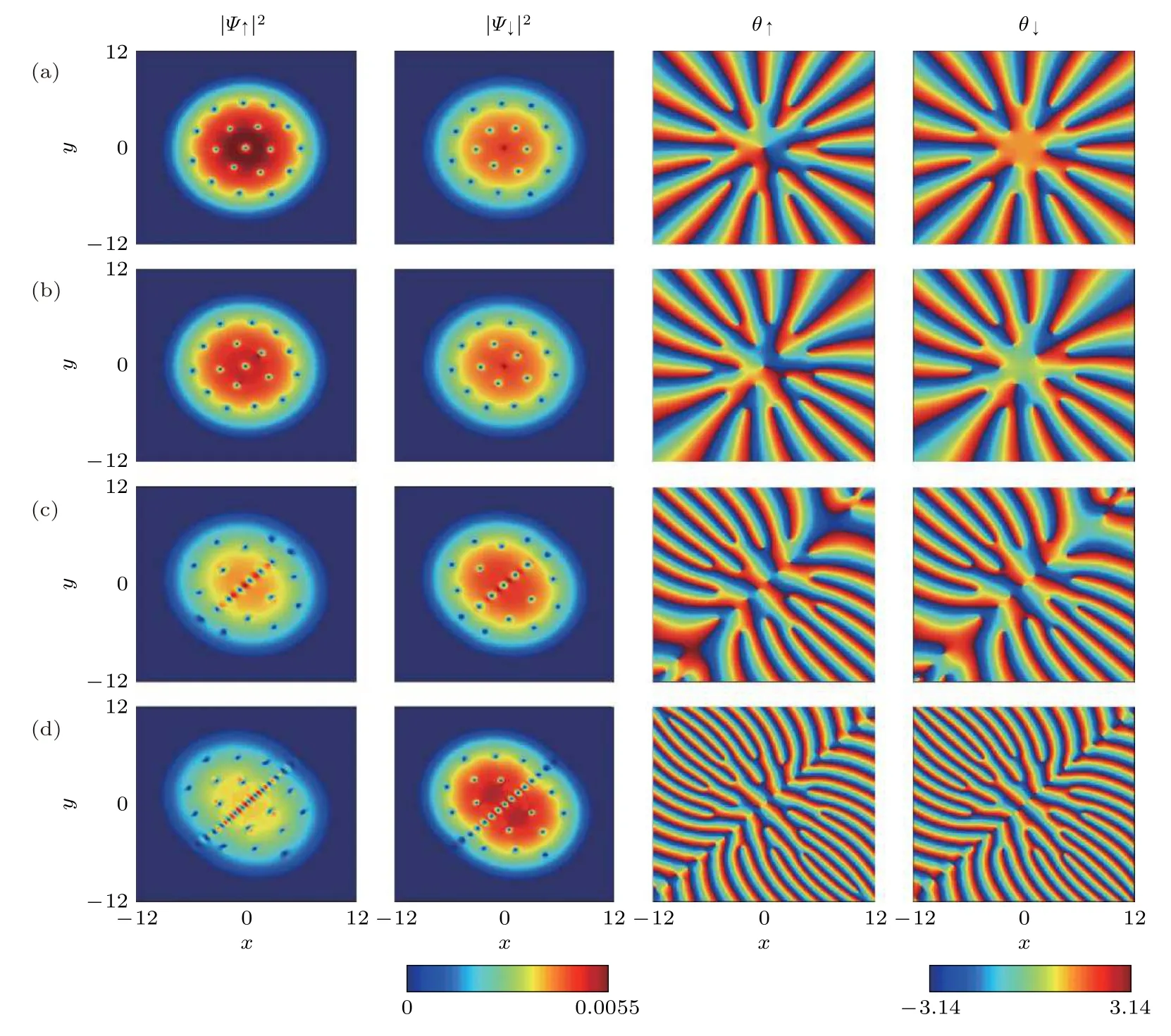
圖10 不同自旋-軌道耦合強度下梯度磁場中兩分量87RbBEC基態粒子數密度分布(第1、2列)和相位分布(第3、4列)[107](a)?(d) 的值分別為 0, 0.2, 0.8, 2Fig.10.Particle number densities (the first and second columns) and phase distributions (the third and fourth columns) of ground state of the two-component BEC of 87Rb for the different spin-orbit coupling strengths: the parameters of in (a)?(d) are 0, 0.2,0.8, 2, respectively[107].

圖11 渦旋的動力學形成[110].渦旋形成于凝聚體的所有分量中, 在y–1分量中占99%以上, 在y0分量中動態渦旋和拓撲渦旋共存Fig.11.Dynamical formation of vortices: vortices are formed in all components, more than 99% of total population is in y–1 component.In the y0 component, dynamical and topological vortices coexist[110].

2008年Ji等[117]研究了自旋1鈉原子BEC中半量子渦旋的動態生成.模擬結果表明, 在外加脈沖磁捕獲勢的情況下, 旋轉光勢阱中可以同時產生獨立的半量子渦旋和渦旋晶格, 同時還發現, 一個明顯的周期調制的自旋密度波空間結構總是嵌入在方形半量子渦旋晶格中.2012年Liu和Liu[118]研究了旋轉和快速淬火的自旋1BEC中由自旋-軌道耦合引起的半skyrmion激發, 給出了描述半skyrmion自旋矢量的三個表達式.結果表明,半skyrmion激發依賴于自旋-軌道耦合和旋轉的結合, 當自旋-軌道耦合強度和旋轉頻率均大于某些臨界值時, 半skyrmion由一個或幾個圓包圍中心, 形成徑向晶格, 即使在強鐵磁(或反鐵磁)凝聚體中也會發生.圖13為旋轉頻率對23Na旋量BEC自旋紋理的影響.

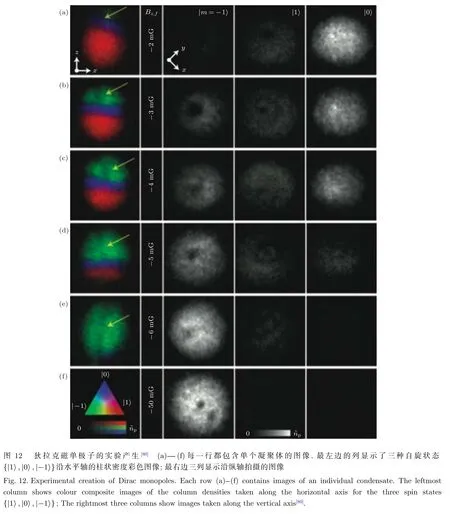
圖13 旋轉頻率對 23Na 旋量 BEC 的影響 [118], 其中 μ j,0(j=0,±1)=3.6 ?ω , μ =25?ω , kx = ky = kz = 1, a0=50aB , and a2 = 55 aB (a) W = 0; (b) W = 0.2 w; (c) W = 0.5 w.第四列顯示了相應的自旋紋理和渦旋的位置Fig.13.The effect of rotation frequency for spinor BEC of 23Na with μ j,0(j=0,±1)=3.6 ?ω , μ =25?ω , kx = ky = kz = 1,a0=50aB, and a2 = 55 aB: (a) W = 0; (b) W = 0.2 w; (c) W = 0.5 w.The fourth column shows the corresponding spin textures and the positions of the vortices[118].

2013年Liu等[119]利用 阻尼映射 Gross-Pitaevkii方程, 研究了二維體系中自旋-軌道耦合的23Na自旋1BEC中的渦旋斑圖, 研究發現較弱的自旋-軌道耦合可以完全破壞不考慮自旋-軌道耦合情況下出現的周期性渦旋晶格; 在自旋-軌道耦合較強的情況下, 各自旋態的渦旋易形成渦旋組,并繞凝聚體中心形成花瓣狀渦旋斑圖.2014年Song等[120]利用精確對角化和平均場理論研究了弱相互作用的自旋-軌道耦合自旋1玻色氣體在外諧波勢阱中的碎裂問題, 研究發現這種碎裂傾向源于總角動量守恒, 且受自旋-軌道耦合強度和自旋相關相互作用的影響.Lovegrove等[121]將鐵磁態無核渦旋通過相位植入法, 在極化態凝聚體中得到了混合態下穩定的無核渦旋.2015年Zhao等[122]在自旋1BEC中解析得到了兩種不均勻的自旋疇構型, 它們分別由正二次塞曼效應和負二次塞曼效應所致.分析表明, 二次塞曼效應可以誘導自旋疇的動態相變, 其符號可以影響自旋模式的拓撲結構.2016年, Gautam 和 Adhikari[123]對零磁化強度的自旋1和自旋2旋量BEC中的分數渦旋進行分類, 并利用精確的數值解和拉格朗日變分近似研究了準二維旋量BEC中渦旋的靜力學和動力學性質.

2017年Liu等[124]通過虛實演化方法研究了具有面內四極磁場自旋1的旋量BEC的基態結構.研究發現, 面內四極磁場和旋轉雙重作用可導致中央Mermin-Ho渦旋的產生; 隨著磁場梯度增強, Mermin-Ho渦旋周圍環繞的渦旋趨向對稱化排布; 在四極磁場下, 密度相互作用和自旋交換相互作用作為體系的調控參數, 可以控制Mermin-Ho渦旋周圍的渦旋數目.Li等[125]研究了鐵磁自旋1BEC中由自旋-軌道耦合引起具有極核旋渦的狄拉克磁單極子, 隨著自旋-軌道耦合強度的增加,具有極核渦旋的狄拉克磁單極子可以轉化為正方形晶格.在自旋-軌道耦合確定的情況下, 增大相互作用強度可引起從具有極核渦旋的狄拉克磁單極子向具有Mermin-Ho渦旋的循環相變.圖14顯示了具有Mermin-Ho渦旋的磁單極子的形成.

5 總結與展望

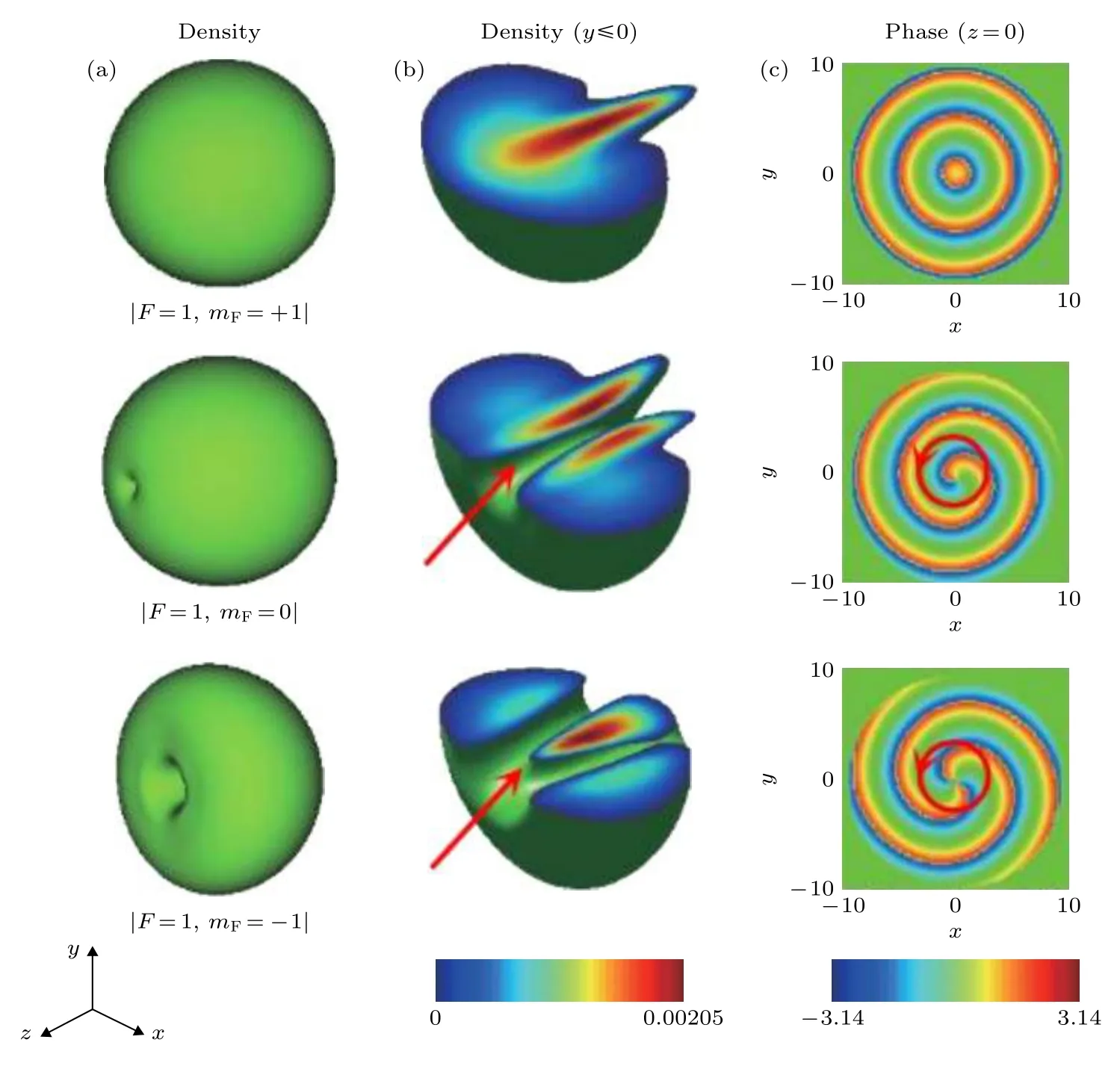
圖14 具有 Mermin-Ho 渦旋的磁單極子[125] (a)等值面的粒子數密度; (b)粒子數密度等深線段 (y ≤ 0), 節點線 (Dirac 線)的位置用紅色箭頭突出顯示; (c) z=0 平面上的位相分布.單渦旋 (mF = 0)和雙渦旋 (mF = –1)具有相同的環流, 由紅圈突出顯示Fig.14.The monopoles with the Mermin-Ho vortex: (a) Isosurface of particle densities; (b) segments of isosurface of particle densities (y ≤ 0).the position of the nodal line (Dirac string) is highlighted by the red arrow; (c) phase distributions in the z = 0 planes.the single vortex (mF = 0) and double vortex (mF = –1) have the same circulations, as highlighted by the red circles[125].

1998年Ketterle研究組首次在自旋為 1的23Na原子系統中實現了BEC, 為冷原子物理開辟了旋量BEC的研究領域.尤其是在超冷原子氣體中人造自旋-軌道耦合的實驗實現, 為研究拓撲量子態提供了一個理想的實驗平臺.本文綜述了旋量BEC的實驗和理論研究, 旋量BEC中產生的拓撲缺陷的種類, 如自旋疇壁、渦旋、磁單極子、skymion、扭結, 著重介紹了兩分量和三分量旋量BEC中拓撲缺陷的研究進展.今后的工作可以推廣到具有高自旋BEC體系, 以及不同自旋-軌道耦合形式的玻色氣體等, 如Rashba自旋-軌道耦合和旋轉勢作用下的鐵磁自旋2BEC中新奇的拓撲結構研究.此外, 在冷原子平臺上研究具有長程相互作用的拓撲缺陷也是未來的一個方向, 以及通過研究自旋-軌道耦合旋量BEC的動力學行為, 并從非平衡過程中來觀察一些拓撲結構, 如馮卡門渦街和量子扭結, 也是非常有意義的工作.