基于Fluent的中間擺臂注射成型工藝參數優化

，，，，

(南京理工大學機械工程學院，江蘇 南京 210094)

0 引言

金屬粉末注射成形( MIM)是一種新型粉末冶金近凈成形技術，它從塑料注射成形行業中引申而來。是將混合料(金屬粉末與非金屬粘結劑的混合物)作為原料，經過注射成形、燒結及后序加工工序，制取金屬材料、復合材料以及各種類型制品的加工制造技術[1]。相比于傳統工藝，MIM技術組織均勻，可制造結構復雜的產品，大大降低了生產成本。

但是MIM的工藝過程復雜，其中最關鍵的一道工序就是注射成型過程，注射成形參數直接影響到產品的開裂、分層、表面塌陷、欠注和內部縮孔等缺陷。在傳統制造過程中往往采用經驗公式和反復實驗來消除缺陷，得到最優的注射工藝參數，這種方法不但成本高昂，而且無法將結果精確量化。隨著有限元法、有限差分法等計算技術和計算機科學的進步，MIM的數值成型模擬研究在近年來受到了更多關注。通過充模過程的數值模擬，不僅可以動態地顯示流體在模具型腔流動過程的溫度、壓力和速度的分布情況，還能預測可能產生缺陷的部位[2]。進而基于分析結果，對工藝參數進行優化，指導實際生產。在此，基于流體力學的基本控制方程，利用Fluent流體計算軟件，對汽車發動機中間擺臂的充模過程進行數值模擬。

1 金屬粉末注射成型多相流控制方程

考慮到MIM充模過程中，注射料通常為金屬粉末和粘結劑的熔體，其一般被視作混合均勻的連續介質，是一種非穩態、非等溫的非牛頓流體。在此，把金屬粉末充模的過程看成是空氣、金屬粉末和粘結劑多相相互作用的過程。混合喂料中，粘結劑的體積分數占比相對更大，是混合料流動的主體，因此主要流體是熔融狀的粘結劑，即為主相，第2相是金屬粉末；除粘結劑和金屬粉末兩相之外，還需要考慮型腔內的空氣的作用，它會隨著喂料的流動而向型腔外部流動[3]，故而將空氣視為第3相。根據流體力學理論，可建立以下方程。

a.質量守恒方程。

(1)

b.動量守恒方程。

(2)

c.能量守恒方程。

(3)

等式的左邊表示單位質量單元的能量與時間的比例關系；右邊分別代表熱傳導，壓力對單位質量流體所做的功、粘性耗散項和重力做功[4]。

2 中間擺臂模型建立和正交試驗設計

2.1 幾何模型及網格劃分

模擬實驗的對象是汽車發動機中間擺臂，其實物如圖1所示。采用ICEM網格劃分軟件，對擺臂的3D模型進行區塊化，生成非結構六面體網格，得到如圖2所示的網格模型。對網格質量進行檢查，六面體單元總數達到38 951個，節點總數達到25 310個。

圖1 汽車中間擺臂注射成形坯 圖2 汽車中間擺臂網格劃分

2.2 喂料物性參數

在此，粘結劑主要由70%的石蠟、25%的聚乙烯和5%的硬脂酸組成；粉末注射成形喂料各組成成分的物性參數如表1所示[5]。

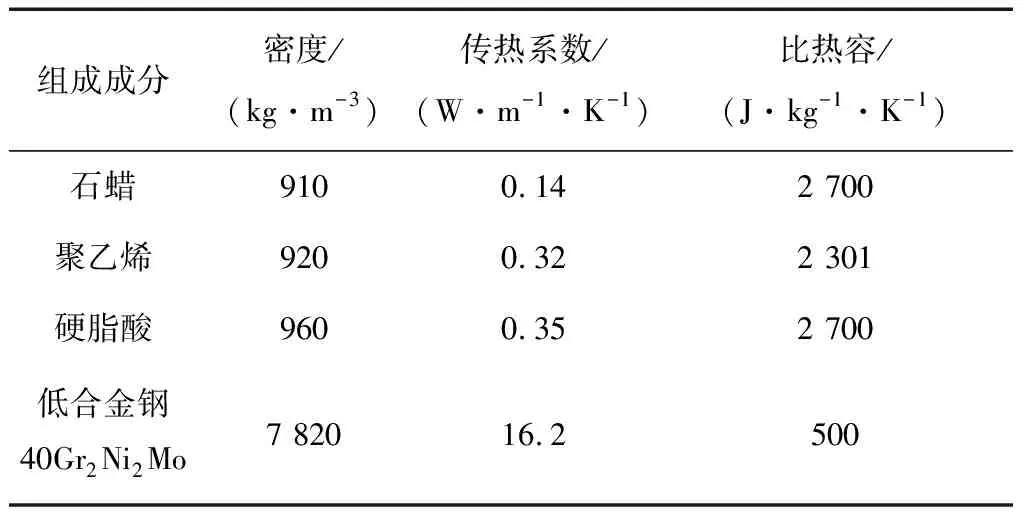
表1 喂料物性參數

根據各組元所占的比例，按體積分數加權計算得到：粘結劑密度ρb=915 kg·m-3;導熱系數λ=0.195 5 W/(m·K);粘度n=0.45;比熱容Cp=2 550.25 J/(kg·K)。

2.3 正交試驗設計

試驗因素水平如表2所示、表頭設計如表3所示、正交實驗因素安排如表4所示。

表2 實驗因素、水平表

選擇在注射成型過程中，充模階段的射膠速度百分率(螺桿最大推進百分率)、熔體溫度和注射壓力作為研究對象。實驗的目的是利用Fluent進行數值模擬，根據Fluent的分析結果，得到最佳工藝參數組合，對實際生產進行指導。實驗以射膠速度百分率、熔體溫度和注射壓力作為3個因素A,B和C，每個因素根據注塑模具的相關經驗公式選取3個水平，且同時研究各因子間的交互作用，故本文采用L27(313)正交表[6]。

表3 實驗表頭

注：AB表示注射速度百分率和熔體溫度之間的交互作用；AC與BC同理。

表4 正交實驗因素安排表

表4(續)

3 邊界條件的設置

3.1 熱傳導邊界條件

考慮到在設計注射模具時，模具具有冷卻系統以保證型腔溫度的穩定，故此處假設模具溫度恒定為25 ℃，即流場外部溫度恒定為25 ℃。已知邊界對流換熱系數α，根據熱傳導控制方程為

(4)

ρ，λ，Cp分別表示模具材料的密度、熱傳導系數和比熱容；Q為熱源相[7]。

3.2 運動邊界條件

在入口邊界上，速度邊界條件根據注射速度計算公式為[8]

(5)

va為螺桿速度百分率(最大螺桿速度的百分率)為a時澆口的注射速度；l為加工該樣件時，螺桿的射出行程；L為螺桿的最大射出行程；C為注射機注射量；S為澆口截面積。計算可得v45%=1.97 m/s，v35%=1.53 m/s，v25%=1.09 m/s。

壓力邊界條件：入口壓力由注射機的實際注射壓力確定；出口處未施加額外壓力，故為標準大氣壓。

4 模擬結果分析

4.1 數值計算結果

根據Fluent模擬結果，可以直觀地看到固相粉末的體積分數。下面主要分析在正交試驗設定工藝參數條件下固相粉末體積分數的分布情況。同時結合實際生產，檢查在各工藝參數條件下生產實驗品的外觀狀況。

固相粉末的分布情況是影響成形坯料密度分布的重要因素，其直接決定制品的力學性能。表5為數值模擬仿真結果和各工藝參數條件下，制品的外觀狀況。

表5 實驗結果 %

4.2 結果分析

由表5中制品的外觀狀況可知，第4、第5、第7、第8、第10、第11、第13、第14、第19、第20和第22組工藝參數組合能得到合格的制品外觀，對比以上11組實驗參數與其他缺陷組，可知：當注射壓力和熔體溫度分別與混合料的流動性成正比，制品容易出現飛邊現象；當注射速度偏低，則制品容易在充模完成前冷卻凝固，從而產生凹坑現象。

基于以上外觀正常的11組試樣，對其固相含量作極差分析。極差的大小與其對應因素對試驗結果的影響程度成正比。直觀分析結果如表6所示，表6中ki(i=1，2，3)是因素的各個水平的平均指標，按ki=∑di/m(m為包含水平i的實驗次數,但未射出的實驗排除在外)計算；di為水平i對應的固相含量；R為各項的極差(R=kmax-kmin)[9]。

表6 實驗結果-極差分析

對比表6中極差分析結果，可知各因子及其相互作用對固相含量W的影響大小：B>A>BC=AB>C>AC。Ai,Bi,Ci(i=l，2，3)表示各因素下，i水平時對應的實驗條件(詳情參照表2)。故優先選擇因素A和因素B，對比因素A和B的3個水平數據，可知應選擇A1B1，但該參數組合外觀上存在缺陷，故因素A取A2，即A2B1。由于BC>C，所以分別對比B1C1,B1C2和B1C3結果，可知固相含量：WB1C3>WB1C2>WB1C1，雖然WB1C3最優，但其存在外觀缺陷，且WB1C1低于WB1C2，故此取B1C2。因此A2B1C2為最優參數組合。此時注射速度百分率為35%，熔體溫度為180 ℃，注射壓力為145 MPa。

5 結束語

將金屬粉末注射成形數值模擬技術和正交試驗設計方法結合，作為優化粉末注射成形工藝參數的有效工具，從而避免單純依靠經驗公式得到工藝參數的盲目性與不可靠性。 對中間擺臂中固相合金粉末的體積分數進行了分析，并基于數值模擬結果，對各實驗參數下，制品各部位固相的體積分數作了對比，得到最優工藝參數組合。 當工藝參數設置為注射速度百分率為35%、注射溫度180 ℃、注射壓力145 MPa時，得到的固相體積分數最高，達到57.56%。