自由活塞斯特林發電機空載磁場模擬及分析

陳 曦， 崔 浩

（上海理工大學 能源與動力工程學院， 上海 200093）

自由活塞斯特林發電機是將自由活塞斯特林發動機和直線發電機耦合在一起構成的，具有熱電效率高、壽命長等優點，能滿足能源高效利用和環境安全的需求。其中，直線發電機與旋轉電機相比，結構簡單、靈敏度高、定位精度高、反應速度快[1]。由于斯特林發動機與直線發電機沒有中間傳動環節，從而減小了機械損耗，提升了機械效率。

按驅動方式，直線電機可分為動圈式、動鐵式和動磁式。動磁式直線電機相對于動圈式和動鐵式，具有結構緊湊、體積小、比推力大、效率高、可靠性高等優點，所以動磁式直線電機更適用于自由活塞斯特林發電機中[2]。在動磁式直線電機中，依據繞組相數可分為單相和三相動磁式直線電機。本文基于復雜性和成本考慮，采用單相動磁式直線電機。

對動磁式直線電機的數學模型進行分析的方法主要有兩種：磁路分析法和有限元法。由于實際磁路結構、邊界和材料等的復雜性和非線性，需要對實際磁路進行一系列的假設和簡化，因此想要通過磁路分析法進行精確解析非常困難，分析結果誤差較大，這種方法多用于直線電機的初步設計。而有限元數值解析法可以借助電磁場軟件對材料的非線性、結構的復雜性進行精確處理，計算結果精確，因此有限元數值分析方法主要用于直線電機的優化設計。

Thales 公司的Benschop 等[3]利用Opera 電磁分析軟件對一臺單磁鋼雙線圈電動機進行了電磁模擬與結構優化。英國Sheffield 大學的Clark 等[4]設計了一臺雙線圈雙磁鋼動磁式直線電動機，應用等效電路法對銅損、線圈匝數、電感等電磁參數進行了初步設計，然后將系統等效為一個非線性變壓器模型，通過有限元分析進行了電動機參數的精確設計。日本的Takahashi 等[5]在未進行解析模型建立與計算的基礎上，直接通過有限元分析對一臺直流線性電動機進行了優化設計，這一方法可以滿足一定的準確性要求。上海交通大學陳楠[6]采用Ansoft Maxwell 電磁場分析軟件對直線電動機的動態和靜態電磁特性進行了數值模擬，揭示了動磁式直線電動機電磁力產生的機理。浙江大學周文杰[7]使用Ansys 電磁場分析軟件對其設計的動圈式直線電動機進行了結構分析和優化，得出了結構尺寸和氣隙厚度對電動機推力的影響。華中科技大學張春平等[8]運用等效磁路原理推導了電動機線圈磁匝鏈的表達式，然后根據電磁能守恒原理，將電動機系統簡化為一個無損的磁儲能系統，通過解析方法，推導了線圈靜態感性阻抗和推力系數的表達式，從能量角度解釋了電學部分與機械部分的耦合原理。趙鏡紅等[9]針對徑向充磁圓筒永磁直線同步電機，介紹了一種基于圓柱坐標標量磁位的分離變量法的磁場解析計算方法，并對大氣隙無槽電機的氣隙磁場分布進行了理論分析，得出氣隙磁場軸向和徑向磁場分布的解析結果。黃克峰等[10]針對軸向充磁圓筒型永磁直線電機的磁場分布和氣隙磁場的計算與徑向充磁問題，提出了一種基于基本氣隙磁場計算軸向充磁圓筒型永磁直線電機磁場的解析計算法。

本文對動磁式直線發電機其磁路結構進行了研究，設計了一種直線發電機磁路結構，采用Ansys/Maxwell 建立了動磁式直線發電機的電磁場仿真模型，模擬得到了直線發電機空載運行時的磁感線分布和磁感應強度分布，并計算了直線發電機的空載感應電動勢。

1 模擬過程

動磁式直線發電機主要包括：動力活塞、托架、永磁體、繞組線圈、發電機初級（即外軛鐵）和發電機次級（即內軛鐵）等，如圖1 所示。永磁體貼在托架上，并與動力活塞固定，共同組成直線發電機的運動部件。工作時，直線發電機初級和次級靜止不動，動力活塞帶動直線發電機的運動部件往復運動，從而實現機械能向電能的轉化。以動力活塞為紐帶，自由活塞斯特林發動機和直線發電機相耦合，最終實現熱能-機械能-電能的轉化。

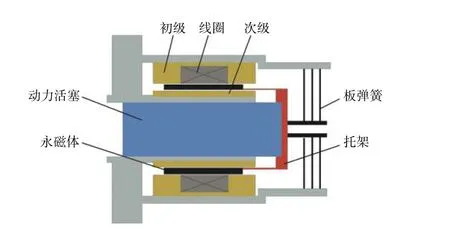
圖 1 直線發電機示意圖Fig.1 Schematic diagram of linear generator

采用Ansys/Maxwell 進行模擬，Ansys/Maxwell是基于有限元法的電磁場分析軟件。所謂有限元法，即將整個區域劃分成很多很小的子區域，這些子區域一般叫做“單元”或“有限元”，把求解邊界問題的原理應用到這些子區域中，求解每個子區域，再把各個子區域的結果綜合起來以得到整個區域的解[11]。

1.1 結構參數

本文所研究的直線發電機的磁路結構為：初級結構采用半閉口平行單槽結構；次級結構采用傳統的圓環式結構；發電機動子由永磁體和兩個輔助極組成，永磁體和輔助極無間隙；永磁體采用徑向沖磁方式。具體結構參數見表1。在永磁體兩端增加輔助極，采用齒尖向內的初級形狀有助于提高繞組磁鏈和感應電動勢。

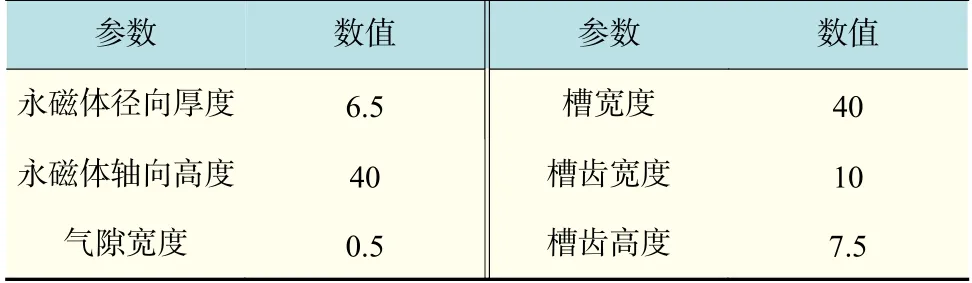
表 1 動磁式直線電機結構參數Tab.1 Structural parameters of moving magnet linear motor mm

1.2 電磁場仿真模型

動磁式直線發電機的二維模型如圖2 所示。整個外部區域均為求解區域，Band 域的作用是將模型中運動部分和靜止部分分開，Band 域內為運動部分。外軛鐵即初級，內軛鐵即次級。

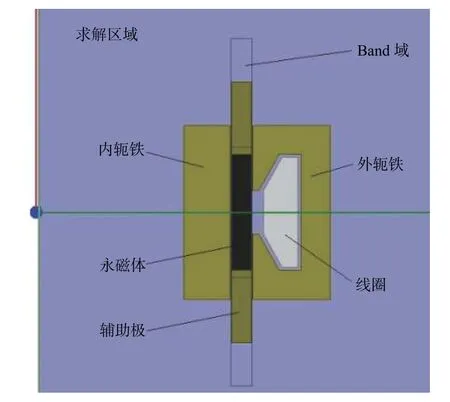
圖 2 發電機二維模型Fig.2 2D model of the generator

1.3 有限元計算

Ansys/Maxwell 有限元求解步驟為：首先確定電磁場求解器，本模型是在Transient 場求解器下建立的。其次確定幾何模型坐標系，根據直線發電機的幾何結構，選擇Cylindrical about Z 坐標系，即關于Z 軸旋轉對稱。之后定義電機結構的材料，氣隙及直線發電機周圍為空氣，相對磁導率μr=1。初級、次級和輔助極用50W470 硅鋼片。線圈繞組材料為銅。永磁體材料為NdFe35，相對磁導率μr=1.099 8，剩磁為1.23 T，矯頑力為890 kA/m。最后設定相應邊界條件，劃分網格，由Maxwell方程組[12]和有關控制方程進行求解。

在有限元求解中，永磁體工作點位于回復線上，回復線是一直線。當永磁體回復線和退磁線重合時，永磁體工作點的磁感應強度B 和磁場強度H 關系為

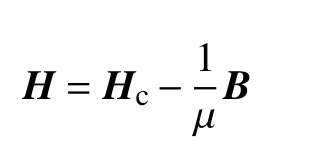
式中：Hc為計算矯頑力；μ 為磁導率，μ=μ0μr，μ0為真空磁導率。

以矢量磁位A 作為求解函數，根據Maxwell方程，直線發電機電磁場的邊值問題可描述為

式中：Js為電流源區電流密度；Ω1 為非永磁區域；Ω2 為永磁區域。

此邊值問題的等價變分問題轉化為求F（A）的最小值，其表達式為

在二維場中，矢量A，Js只有軸向分量。Hc可表示為

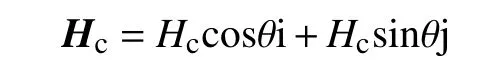
式中，θ 為磁化方向和x 軸的夾角。這就得到了關于永磁體的控制方程。

Maxwell 方程的微分形式表示為

式中，v 為運動物體的速度。

采用瞬態求解時，直線發電機模型一部分固定，這部分速度為零。運動部分處于自身坐標系，偏時間導數轉變為矢量磁位A 的全時間導數，所以運動方程變為

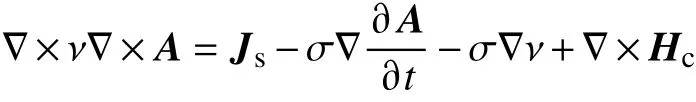
求解上述方程就可獲得直線發電機運動中任意時刻任意一點的矢量磁位，進而可推導電磁場中其他的場量。

2 空載磁場分布

直線發電機在空載運行時，發電機的線圈繞組開路，發電機處于空載狀態。自由活塞斯特林發動機驅動直線發電機動子作往復直線運動，永磁體產生的磁場與直線發電機線圈繞組之間有相對運動，所以直線發電機的線圈繞組中會產生感應電動勢，但無法形成電流，故沒有電流對永磁體產生主磁場的影響，即直線發電機的磁場完全由永磁體提供。

永磁體產生的空載磁場強度和永磁體運動中的磁場分布規律對直線發電機空載感應電動勢影響極大。因此，準確計算直線發電機的參數和性能首先要得到直線發電機的磁場分布。

2.1 磁感線分布

圖 3 磁感線分布Fig.3 Distributions of magnetic induction lines

圖3 所示為發電機動子運動時不同時刻t 永磁體產生的磁感線分布。從圖3 可以看出，0 s 時，動子處于初始平衡位置，磁感線主要集中在齒尖處，軛部和齒部基本沒有磁感線，此時主磁通基本為零；0.005 s 時，動子處于位移正向最大位置，主磁通達到最大，存在少量漏磁；0.01 s 時，動子回到平衡位置，這是磁感線分布與初始時刻基本相同；0.015 s 時，動子處于位移負向最大位置，磁感線分布與0.005 s 時磁感線分布相似，同樣存在少量漏磁。

2.2 磁感應強度分布

圖4 所示為直線發電機動子運動時不同時刻t 的磁感應強度分布云圖，紅色代表磁感應強度最大，藍色代表最小，其他顏色代表處在最大值與最小值之間。從圖4 可以看出，當動子處于平衡位置時，初級齒尖磁感應強度較大，而初級齒部和軛部磁感應強度較小；當直線發電機動子運動到位移正、負向最大位置時，初級齒尖的磁感應強度同樣較大，所以在進行磁感應強度分析時要重點關注初級齒尖的磁感應強度大小。

圖 4 磁感應強度分布Fig.4 Distributions of magnetic induction intensity

3 空載感應電動勢計算

準確計算出直線發電機的空載感應電動勢是有助于對其進行性能分析和深入優化設計的。本文采用Ansys/Maxwell 模擬計算直線發電機的空載感應電動勢。通過對直線發電機的有限元分析，可利用法拉第電磁感應定律來計算直線發電機空載感應電動勢。

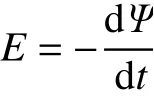
式中：Ψ 為總磁鏈；t 為時間。

首先，需要獲得動子在不同位置時定子繞組線圈中的磁鏈分布。動子速度為自由活塞斯特林發動機熱力學和動力學設計給出，速度2.513 cos(100 πt)，m/s，其中：f 為頻率；X 為振幅8 mm；t 為時間。

直線發電機動子運動到不同位置時，永磁體發出的磁通經過直線發電機的永磁體、氣隙、初級、輔助極和次級等匝鏈繞組線圈形成回路。對匝鏈繞組線圈截面的磁鏈進行積分求和，便可以得到繞組線圈中總磁鏈與時間的關系。再對總磁鏈進行求導便可得到直線發電機繞組線圈中產生的空載感應電動勢。直線發電機磁鏈和感應電動勢的一個周期變化如圖5 所示。從圖5 可以看出，直線發電機空載感應電動勢呈現正弦變化趨勢，在波峰波谷未發生明顯畸變。

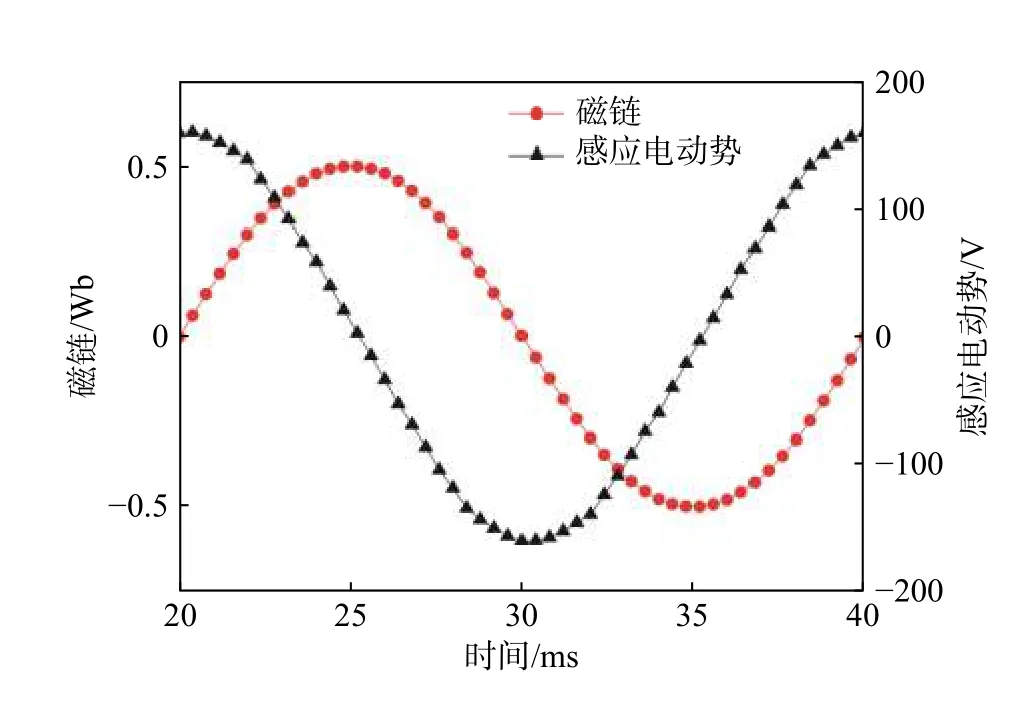
圖 5 磁鏈和感應電動勢隨時間變化圖Fig.5 Flux and induced electromotive force vs. time

空載感應電動勢的有效值U 表征了直線發電機輸出電壓的能力，可表示為

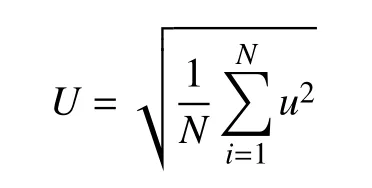
式中：N 為一個周期的取點個數，N 值越大，有效值計算越精確；u 為空載感應電動勢瞬時值。

根據上式可求得空載感應電動勢的有效值U 為111.22 V。

4 總 結

針對自由活塞斯特林發電機中的動磁式直線發電機，設計了一種磁路結構，即在永磁體兩端增加輔助極，采用齒尖向內的初級形狀，這種磁路結構減小了漏磁，有助于提高繞組磁鏈和感應電動勢。建立了此磁路的動磁式直線發電機電磁場仿真模型，采用Ansys/Maxwell 進行數值模擬，得到了空載運行時不同位置的磁感線分布和磁感應強度分布云圖，發現不論動子運行到任何位置，齒尖位置的磁感應強度總是最大，所以在進行磁感應強度分析時要重點關注初級齒尖的磁感應強度大小。