代數體函數與其k 階導數的唯一性
朱新瑤, 劉曉俊
(上海理工大學 理學院,上海 200093)
1 問題的提出
本文涉及的代數體函數值分布論的相關概念和記號參見文獻[1-2]。
對于具有公共值的亞純函數的唯一性問題國內外眾多專家學者進行了廣泛研究,得到了許多結果[3-11],其中一個有意義的方向是與其導數具有公共分擔值的亞純函數的唯一性問題。
1983 年,Gundersen[2]證明了定理A。
定理A設 f(z)為 非常數的亞純函數, a,b為兩個互異的有限復數,若 f(z)和 f′(z)C M 分擔 a,b,則f(z)= f′(z)。
1986 年,Frank 等[12]證明了定理B。
定理B設 f(z)為 非常數亞純函數, a,b為兩個互異的有限復數,若 f(z)和 f(k)(z)C M 分擔 a,b,則有f(z)= f(k)(z)。
自然地,我們會考慮如何將上述結果推廣到代數體函數。代數體函數是一種比亞純函數更為廣泛的多值函數,它由不可約方程
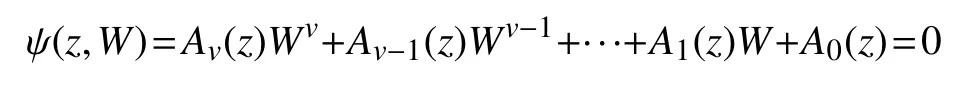
來確定,其中 Av(z),···,A0(z)是復平面上一組沒有公共零點的解析函數。特別地,當Av(z),···,A0(z)都為多項式時,W (z) 為 代數函數。本文假設Av(z),···,A0(z)中 至少有一個是超越整函數。當 v ≥2時,W(z) 為 多值函數;當 v=1時 , W(z)就是亞純函數。顯然, v值代數體函數是亞純函數的自然推廣。在本文中代數體函數 W(z) 的 一階導數記作 W′(z) , k階導數記作 W(k)(z),它 們都為 v值代數體函數。
關于代數體函數的唯一性問題,劉慧芳[13]將定理A 推廣到代數體函數,得到了定理C。
定理C設 W(z) 為 v(v≥2)值 代數體函數,a1,a2,···,a2v為 2v 個互 異 的有 限復 數,若 W(z) 與 W′(z)CM 分擔 a1,a2,···,a2v且 IM 分擔 ∞, 則 W(z)=W′(z)。
當 v=1時,定理C 即為定理A。
參照文獻[13]中的定義方法,現給出如下記號: W(z) 和 M(z)為 v 值 代數體函數, a為任意復數,且 W(z) 和 M(z)分 擔 值a。若 z0是 W(z)?a 的 u重零點時,也是 M(z)?a的 至少 u重零點,則記為:W(z)=a →M(z)=a。 特別地,W(z)=∞→M(z)=∞則 表 示 W(z) 的 u重 極 點 是 M(z)重 數 至 少 為 u的極點。
本文考慮將定理B 推廣到代數體函數,得到定理1。
定理1設W (z) 為 v (v ≥2)值 代數體函數,a1,a2,···,a2v為 2 v 個非零互異有限復數。若W(z)=ai→W(k)(z)=ai(i=1,2,···,2v), 且IM 分擔 ∞, 則 W (z)=W(k)(z)。
由此,可得推論。
推論設 W(z) 為 v(v ≥2)值 代數體函數,a1,a2,···a2v為 2v 個 互異 的 有 限復 數,若 W(z) 與 W(k)(z) CM 分擔a1,a2,···,a2v且 IM 分擔 ∞, 則 W (z)=W(k)(z)。
此外,通過對定理C 證明過程的分析可以看出,當v ≥3時 ,定理中分擔值的個數可以減為(2v?1)個,即得到定理2。
定 理2設 W(z) 為 v(v ≥3)值 代 數 體 函 數,若W(z) 與 W′(z) C M 分擔包括0 在內的 2v?1個有限復數且IM 分擔 ∞, 則 W (z)=W′(z)。
2 相關引理及其證明
引理1設 W(z)為 v 值 代數體函數,若 W(z)與W(k)(z) IM 分擔 ∞,則有:

證明設
所以
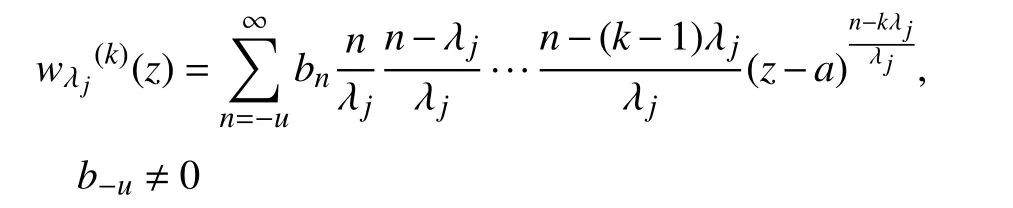
若W(z)與W(k)(z)IM分擔∞,則有
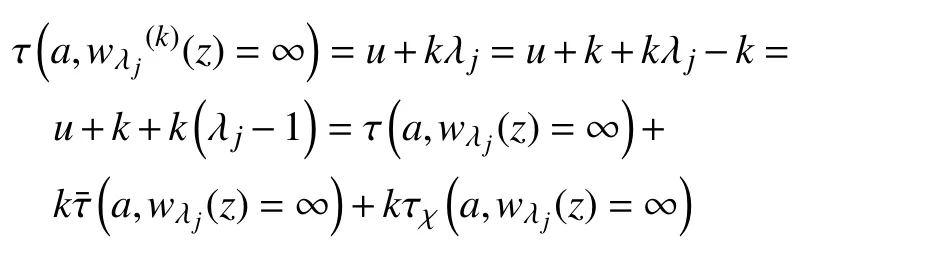
所以
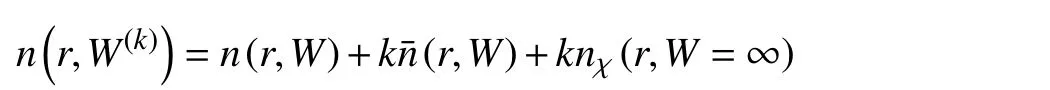
因此,結論a 成立。

因此,結論b 成立。
引理2[14]設 W (z) 為 v 值代數體函數,則
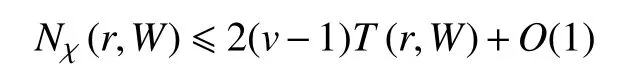
引 理3[14]設 W(z) 為 v 值 代 數 體 函 數,且a1,a2,···,aq為 擴充復平面上 q個互異復數,則
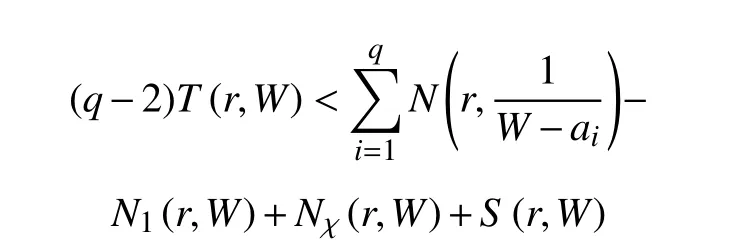
其中, N1(r,W)是 W (z) 重 值點的密指量, τ重值點計算 τ ?1重。
引理4[15]設 W(z) 為 v 值 代數體函數,且a1,a2,···,aq為 q個互異復數,則
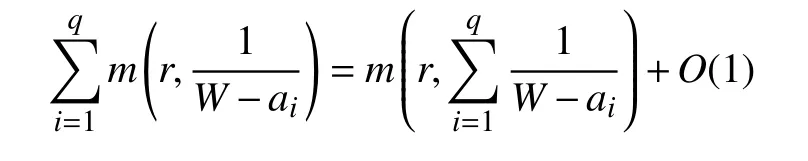
引 理5設 W(z) 為 v 值 代 數 體 函 數,且a1,a2,···,a2v為復平面上 2v個互異非零有限復數。若W(z)=ai→W(k)(z)=ai,i=1,2,···,2v,則有
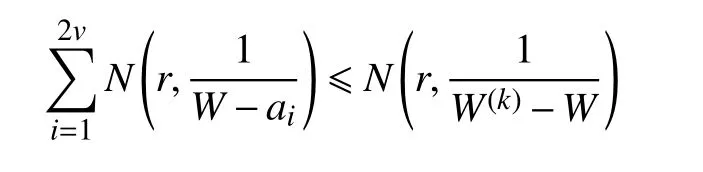
證 明) 設 2v 個 非(零 有 限 復 數)為 a1,a2,···,a2v,
則
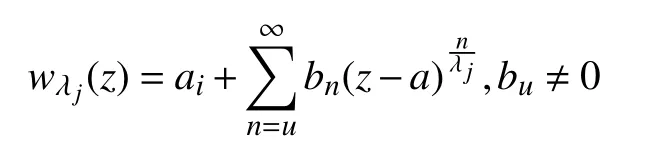
k次求導后有
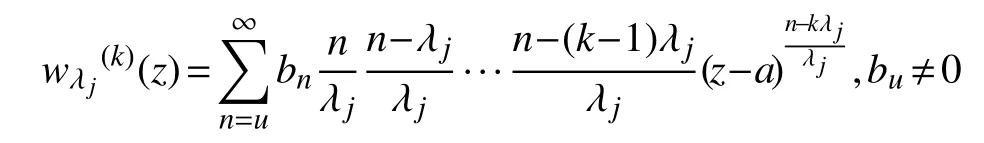
設
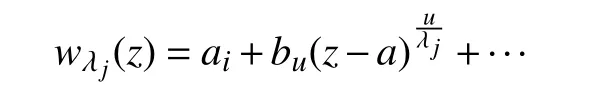
由引理5 條件可得
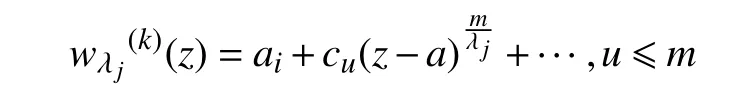
由以上討論可得

因此有
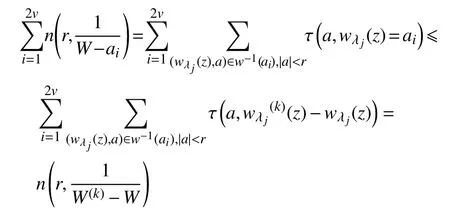
所以
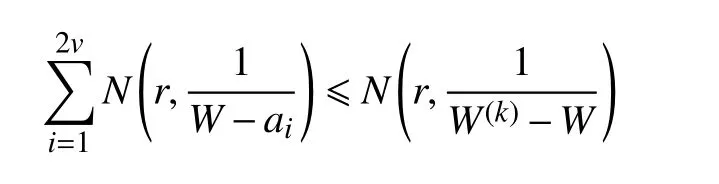
證畢。
3 定理證明
3.1 定理1 的證明
證明設 2v 個 非零有限復數為 a1,a2,···,a2v。反證法,倘若 W(z)≠W(k)(z) , 令 q=2v+1,a2v+1=∞,則由引理3 可得

又由引理2 可得
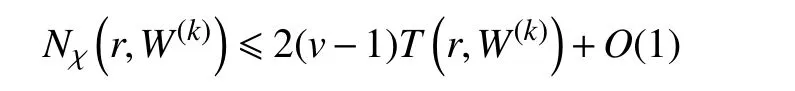
所以,式 (1)可整理為
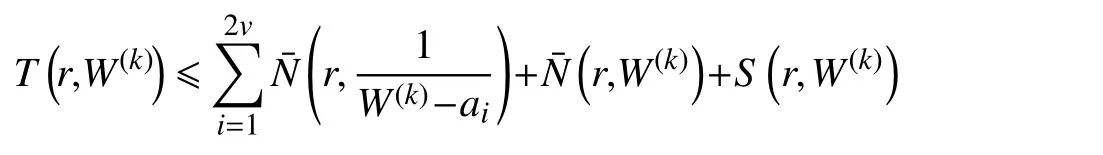
由定理1 條件可得
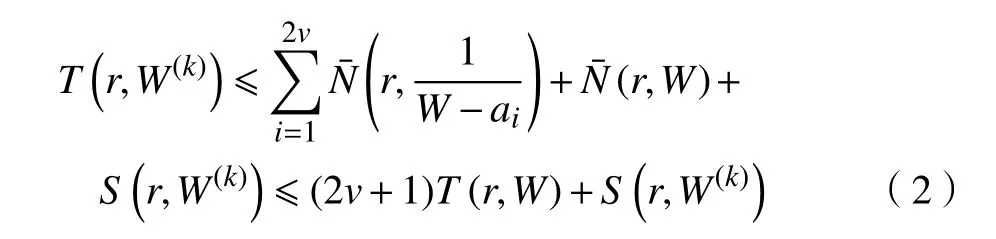
由式(2)可得S(r,W(k))=S(r,W)。
又
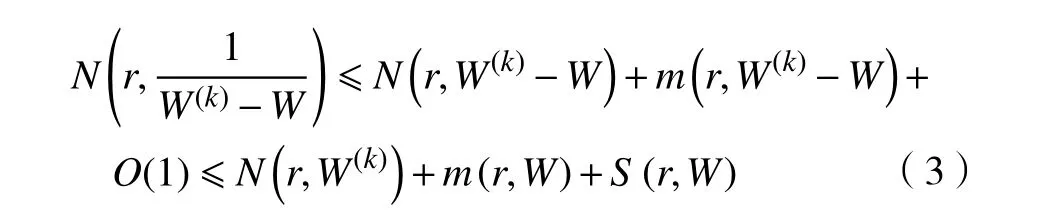
由引理1 的結論a,式(3)可整理為
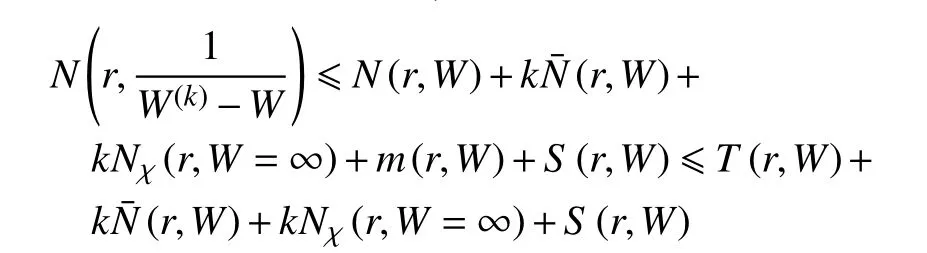
又W(z)=ai→W(k)(z)=ai,i=1,2,···,2v,由引理5 可得
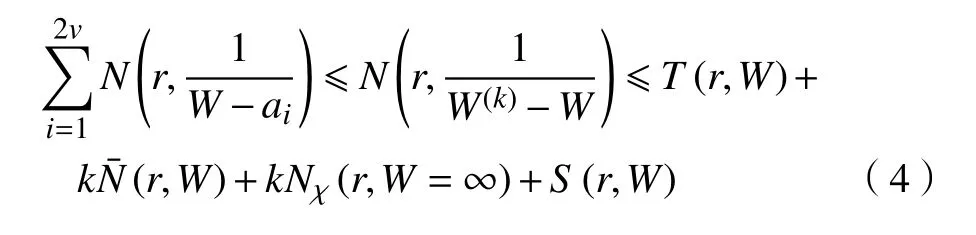
由引理4 可得
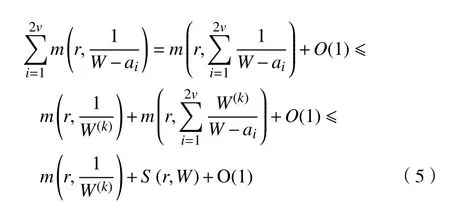
結合式(4)和式(5)可得
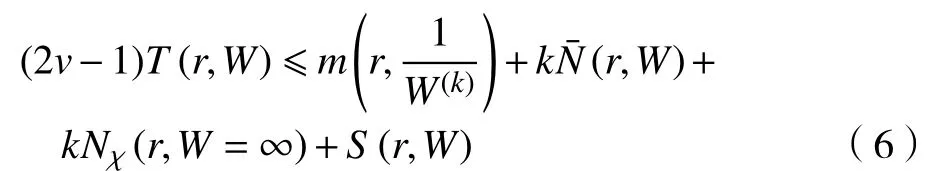

結合式(6)和式(7)可得

3.2 定理2 的證明
證 明倘 若 W(z)≠W′(z), 設 W(z) 與 W′(z) CM 分擔a1,a2,···,a2v?1, 且不妨設 a2v?1=0,a2v=∞。因為W(z) 與 W′(z) CM 分 擔0,則0 為 W(z) 與 W′(z)的Picard 例外值,則有所以
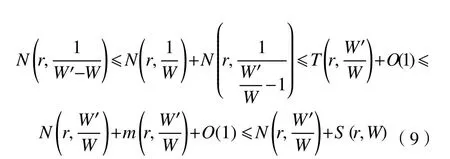
由參考文獻[4]中的引理2.3 將式(9)整理為
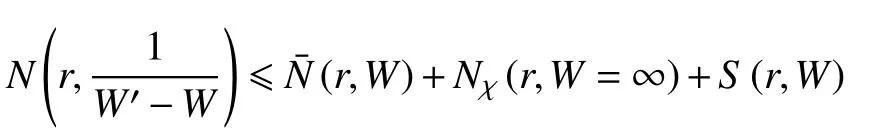
與定理1 的證明類似,由 W(z) 與 W′(z) CM 分擔a1,a2,···,a2v?1,可得
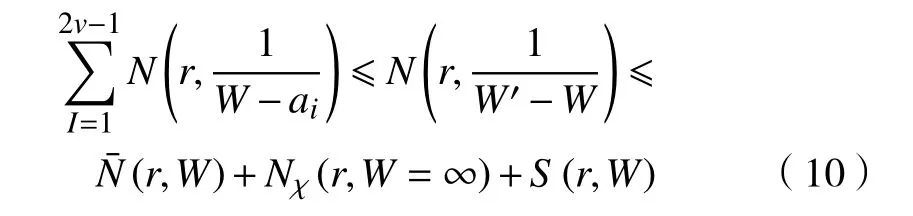
又

結合式(10)和式(11)可得
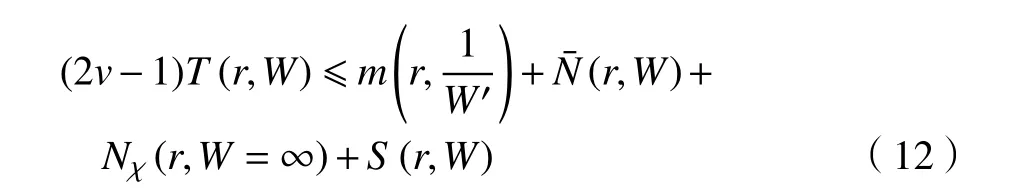
由引理3 和分擔條件可得
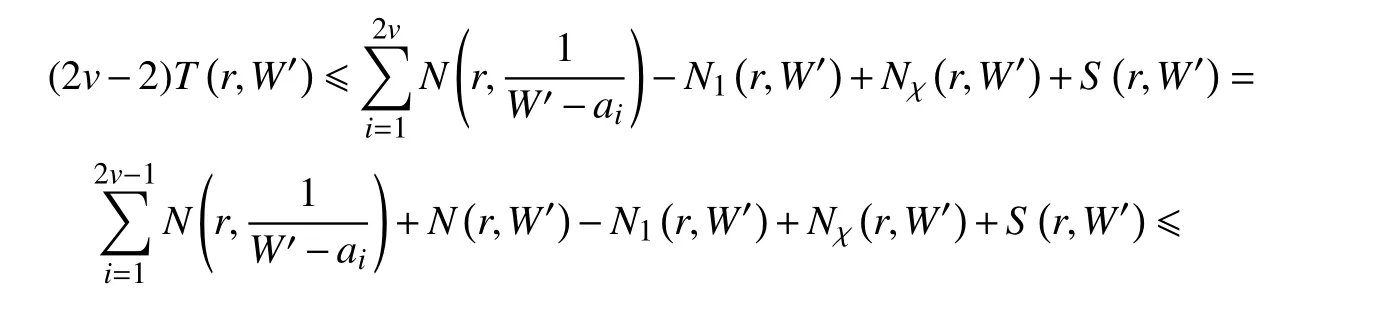
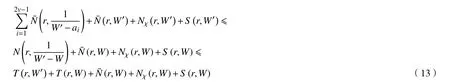
結合式(12)和式(13)可得
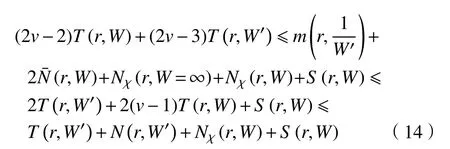
整理式(14)可得(2v?5)T(r,W′)≤S(r,W),v ≥3,矛盾。證畢。

