基于動態軸荷的電動汽車再生制動策略研究

李佳偉 敖銀輝

（廣東工業大學，廣州 511400）

主題詞：再生制動 制動力分配 模糊邏輯估算 動態軸荷

1 前言

電動汽車再生制動系統主要由機械摩擦制動與電機再生制動兩部分組成[1]。電機再生制動是根據電機的電動機/發電機可逆性原理將車輛部分動能轉化為電能儲存在能量儲存裝置中。傳統的制動力分配策略是使前輪與后輪同時抱死或前輪先抱死，以避免發生后軸側滑。對于后輪驅動的車輛，由于采用傳統制動力分配策略時后輪制動力相對較小，制動中可回收的能量相比于前輪驅動更少。Zhang Junzhi等人[2]修改了傳統的β曲線，使其更好地逼近理想的制動力分配曲線，為后驅車輛提供更強的能量再生能力。Mehrdad Ehsani[3]進行了再生制動系統與ABS之間協調工作的研究。Hayashida等[4]將動力電池和超級電容組合為能量供給及回收系統，更有效地回收制動能量。Gao Yimin[5-6]和Hoon Yeo[7]分別提出了各自的前、后輪制動力分配模型，并進行了再生制動系統的設計。Panagiotidis與Delagrammatikas等以并聯式混合動力電動汽車為研究對象建立了再生制動系統模型,并進行了仿真分析,對再生制動系統的制動作用以及能量回收的影響因素進行了系統分析[8]。

在上述方法中，研究者所提出的制動力分配策略都是按固定的前、后軸荷比例分配制動力，沒有考慮在實際制動或加速過程中懸架的非線性變形造成前、后軸載荷的轉移。為此，本文提出一種基于動態軸荷的制動力分配策略，建立以制動強度、車速和電池荷電狀態（State Of Charge，SOC）作為輸入變量，期望的再生制動力作為輸出變量的模糊邏輯控制模型，并在ADVISOR中進行仿真驗證。

2 車輛動力學分析

本文從再生制動效率的角度考慮了懸架非線性變形對再生制動系統的影響，建立了7自由度整車模型，如圖1所示。

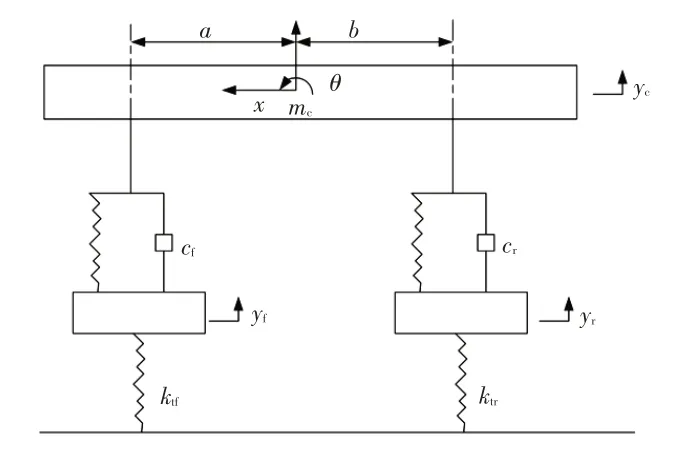
圖1 7自由度汽車懸架非線性幾何簡化模型

非線性彈簧的彈性-位移方程為：

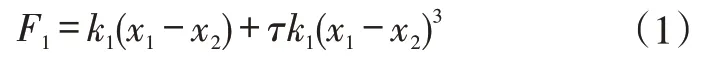
式中，F1為彈簧彈力；k1為彈簧剛度系數；τ為彈簧的非線性系數；xi(i=1,2)為彈簧第i段位移。

根據式（1），車輛行駛時的懸架力為：

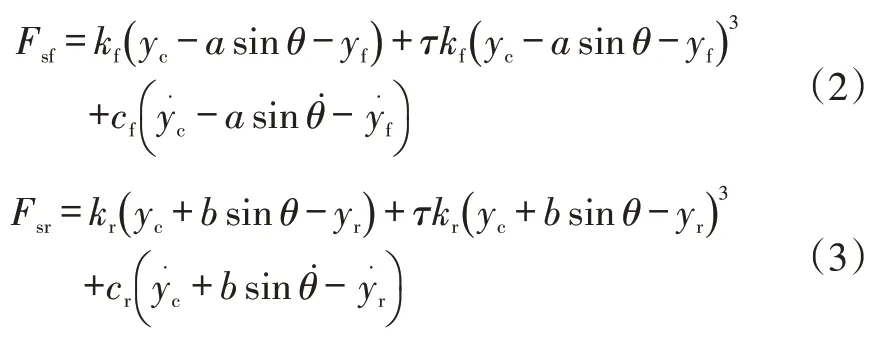
式中，Fsf、Fsr分別為前、后軸的懸架力；yc為簧載質量位移；a、b分別為汽車質心到前、后軸中心線的距離；θ為制動時的俯仰角；kf、kr分別為前、后懸架的彈簧剛度；yf、yr分別為前、后懸架的非簧載質量位移；cf、cr分別為前、后懸架的阻尼系數。

簧載質量運動方程為：

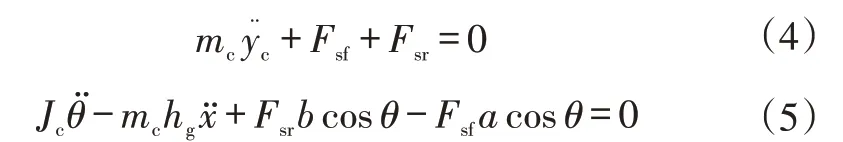
式中，mc為簧載質量；Jc為簧載質量的俯仰轉動慣量；hg為汽車質心高度。

非簧載質量運動方程為：

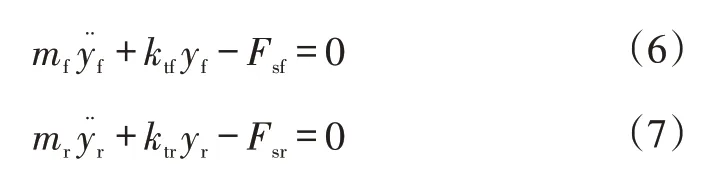
式中，mf、mr分別為前、后懸架非簧載質量；ktf、ktr分別為前、后輪的垂直剛度。

圖2所示為車輪受力情況，車輪的運動方程為：

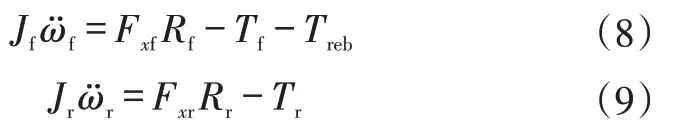
式中，Jf、Jr分別為前、后輪的轉動慣量；ωf、ωr分別為前、后輪的角速度；Fxf、Fxr分別為來自地面的前輪和后輪的制動力；Rf、Rr分別為前、后輪的滾動半徑；Tf、Tr分別為制動時前、后輪上的制動力矩；Treb為電機提供的轉矩。

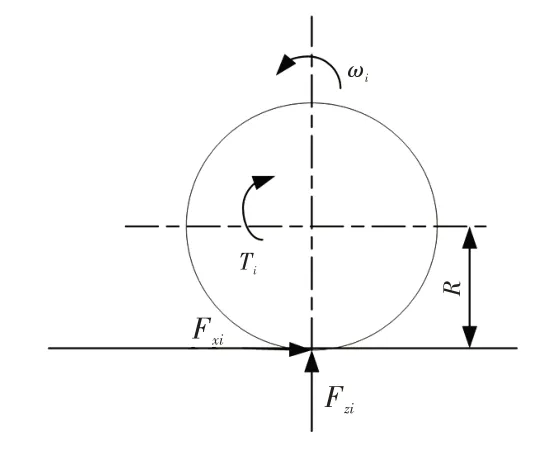
圖2 車輪受力分析

車輪在地面上的垂直載荷為：

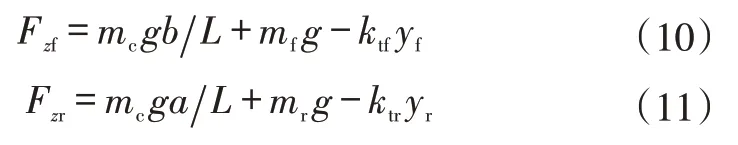
式中，Fzf、Fzr分別為前、后軸地面法向反作用力；L為軸距；g為重力加速度。

汽車的縱向動力學方程為：

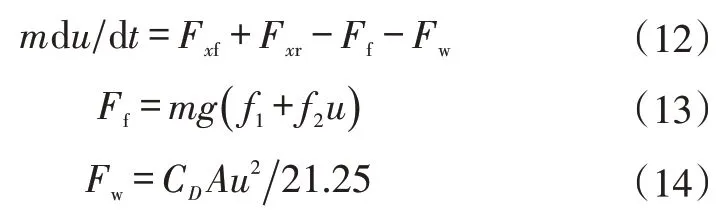
式中，Ff為輪胎滾動阻力；Fw為空氣阻力；f1、f2為滾動阻力系數；m為汽車總質量；CD為空氣阻力系數；A為車輛的迎風面積；u為車速。

3 再生制動策略

3.1 理想制動力分配策略

再生制動系統的結構可依據電動機和摩擦制動系統協調工作的方式分為串聯和并聯兩類。本文的研究對象采用串聯結構，電動機和摩擦制動力可以單獨控制。針對不同情況，傳統再生制動分配策略主要包括理想制動力分配策略、并行制動力分配策略和最佳能量回收分配策略等。

理想再生制動力分配策略基于線性車輛模型，不考慮懸架變形：

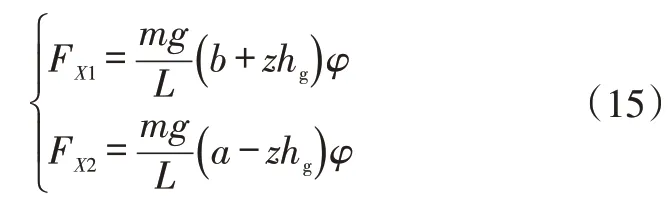
式中，FX1、FX2分別為前、后車輪制動力；z為制動強度；φ為輪胎與路面間的附著系數。

實際制動或加速過程中，懸架的非線性變形會造成前、后軸載荷的轉移，其程度受制動強度的影響。由于理想制動力分配策略依據前、后軸荷比例分配制動力，因此軸荷變化時前、后制動力分配也會發生變化：

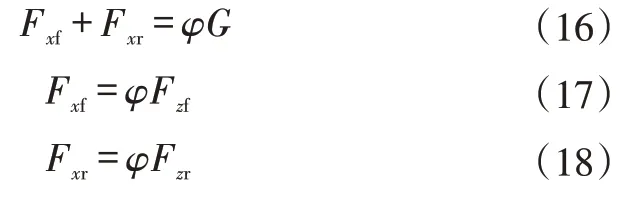
式中，G為整車重力。

3.2 基于動態軸荷的制動力分配策略

本文采用基于動態軸荷的制動力分配策略：通過位移傳感器測量前、后懸架的非簧載質量位移yf、yr，由式（10）、式（11）計算出前、后軸載荷，然后根據實時的前、后軸載荷Fzf、Fzr與模糊邏輯估計的附著系數φ來確定前、后輪制動力分配系數。

車輛在行駛時有加速、勻速、減速（制動）3種工況，而加速與減速都會引起懸架的變形，當且僅當車輛處在制動工況下，位移傳感器檢測的前、后懸架非簧載質量位移是有效的。

為了在保證安全的情況下盡可能多地回收能量，將制動按強度分為3種，即緊急制動、中等制動和輕制動。當車輛處于緊急制動工況時，制動強度很快達到甚至超過0.8，此時制動力完全由機械制動力提供；當制動強度小于0.1時，車輛處于輕制動工況，制動力完全由驅動輪（前輪）提供，后輪制動力為零，此時制動回收能量最多。當制動強度大于0.1時，前、后輪制動力按式（17）、式（18）進行分配。制動力計算分配過程如圖3所示。

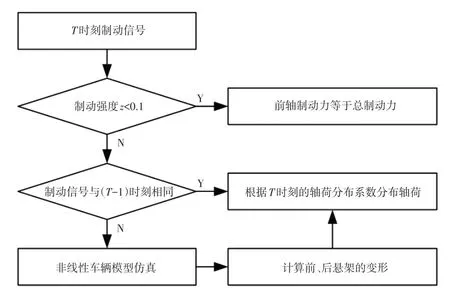
圖3 基于動態軸荷的制動力分配流程

4 基于動態軸荷的制動力模糊控制策略

4.1 模糊控制結構

電動車再生制動時的制動力分配受很多因素影響，且很多參數實時變化。由于模糊控制策略適用于被控對象的數學模型不精確的情況且具有魯棒性強等優點，因此將模糊控制理論應用于純電動汽車再生制動系統制動力分配中。

本文采用雙模糊控制結構，如圖4所示，其中Fbf、Fbr分別為前、后軸制動力，K為再生制動力系數，Fmf為前軸機械制動力，由摩擦制動器提供，Freg為前軸再生制動力，由電機提供。

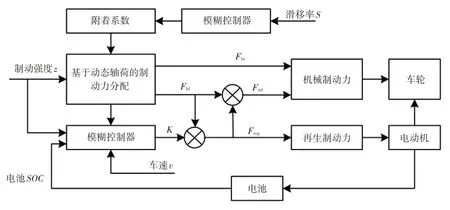
圖4 模糊控制結構

4.2 基于模糊邏輯的附著系數估算

輪胎與路面間附著系數的估算中，基于輪胎模型的估算方法一直占據主導地位。其對車輛動態運動狀態進行測量，例如車輪轉速和車輛加速度。由于輪胎模型法所需要測量的數據較多，計算相對復雜，要實現實時的φ值估算較為困難。因此，本文提出一種基于模糊邏輯的附著系數估計方法，不依賴于任何具體的輪胎模型，只需要對車輪滑移率進行估計。

車輛制動時，車輪中心速度vw大于車輪輪邊線速度vb，輪胎與地面會產生相對滑動。隨著制動強度的增加，滑動成分占比越來越大。一般用滑動率S表示滑動成分的占比：

式中，Re為車輪滾動半徑；ωw為車輪角速度。

由式（19）可知，汽車的滑移率由車速和輪速決定。本文使用卡爾曼濾波算法估算車輛的滑移率，該算法是使用車輛系統模型當前時刻的狀態測量信息以及前一時刻的車輛狀態估計信息，通過遞推公式獲得目前時刻所估計狀態的值，可以極大地提高計算效率，在實際應用中更加方便、簡單，易于實現。

車輪在車輛空載時半徑為R0，在實際運動過程中，受路面和環境因素影響，Re不斷變化。對于兩驅車，從動輪的滑移率較小，因此以由從動輪處獲取的車身速度為研究對象，用車輪變形系數?來表示從動輪滾動時的受壓情況：

則車速為：

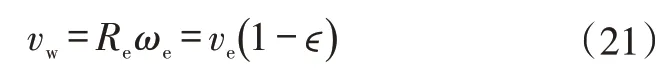
式中，ωe為從動輪角速度；ve為從動輪輪速。

根據卡爾曼濾波算法，可得：

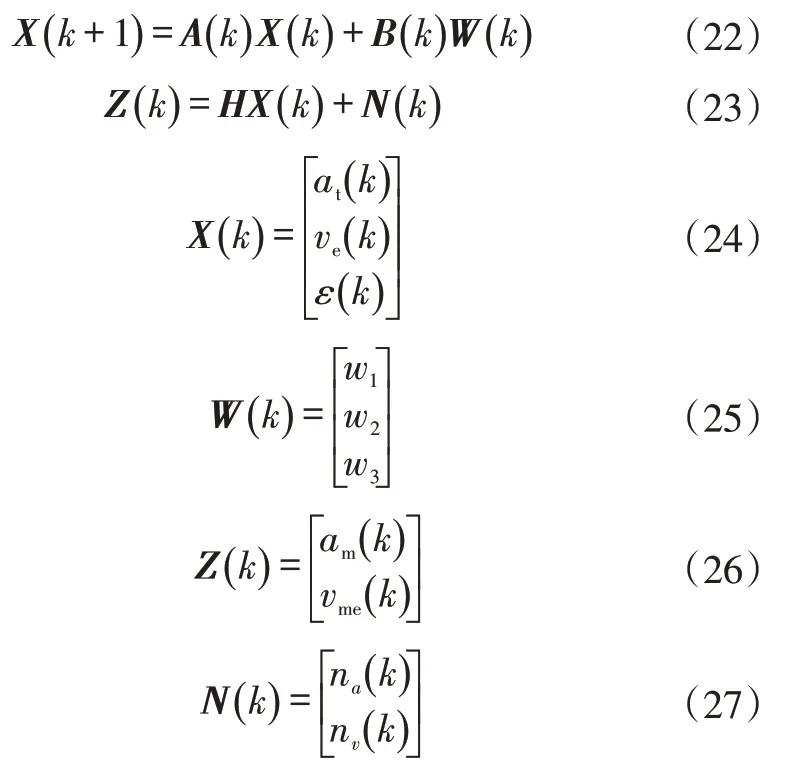
式中，A、B、H為系數矩陣；at為車輛的加速度；am為測量加速度；na為加速度測量噪聲；vme為車速測量值；nv為車速測量噪聲；w1、w2、w3為系統噪聲。

經過卡爾曼濾波后，得到車輪速度ve和車輪變形系數?。由式（21）得出車速vw，車輪角速度ωw可測量獲得，再通過式（19）便可實時估算車輪的滑移率。

附著系數φ與滑移率S的關系曲線如圖5所示，從圖5中可以看出，當滑移率位于ε段時，附著系數達到最大值，之后隨著滑移率的增大，附著系數逐漸減小。

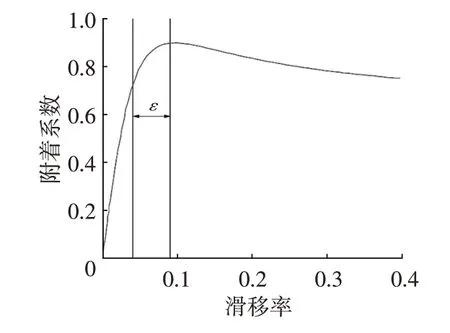
圖5 附著系數-滑移率曲線

本文所提出的最佳附著系數估算方法是為了最大限度地利用路面-輪胎附著力，使前輪或后輪制動力接近抱死極限。

本文以車輪滑移率S為輸入變量，采用Mamdani型模糊控制器實現附著系數的變化量Δφ的控制。

滑移率S、附著系數變化量Δφ的模糊子集均為{L（低）,M（中）,H（高）}，域范圍分別為[0,0.3]、[-0.2,0.2]，隸屬函數如圖6、圖7所示。

將一段時間內的減速需求離散化，并將其劃分為固定持續時間的n個時間步長，φ的估計值為：

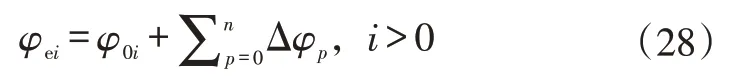
式中，p為時間樣本；φei為當前時間步長的估計值；φ0i為前一時間步長的估計值；Δφp為當前時間步長中的估計值的變化；i為在連續的時間步驟中連續要求減速的次數。

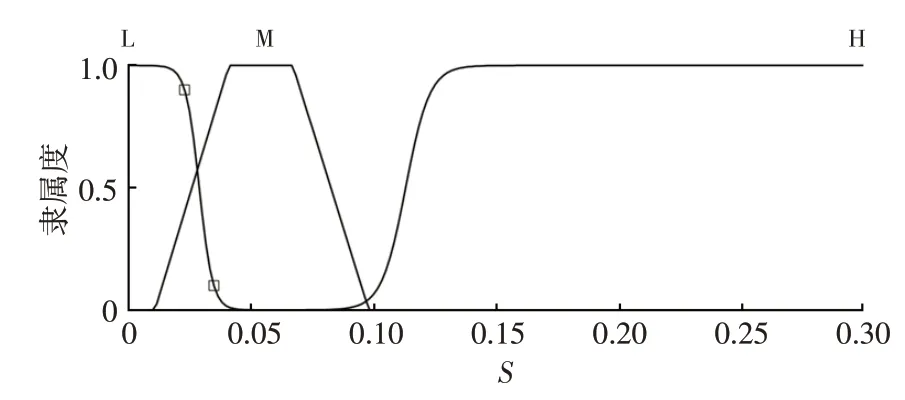
圖6 滑移率S的隸屬函數

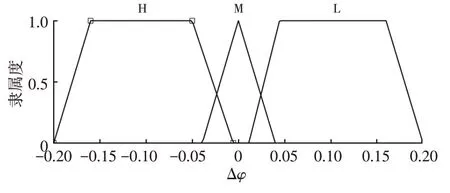
圖7 附著系數變化量Δφ隸屬函數

在制動過程中，先前的減速樣本的估計值φe,i-1保留為初始的φ估計，并將其作為后續制動期間的φ估計。在每個制動事件結束時，φ估計都將停止。

4.3 基于模糊邏輯的再生制動系數估算

再生制動系數模糊控制器采用三輸入單輸出的結構，輸入變量分別為電池SOC、車速v和制動強度z，輸出為前軸再生制動力占前軸總制動力的比例K。

該模糊控制器的輸入量模糊子集為：車速E(v)={L,M,H}，域范圍為[0,100]km/h，制動強度E(z)={L,M,H}，域范圍為[0,1]，荷電狀態E(SOC)={L,M,H}，域范圍為[0,100%]。輸出變量再生制動系數的模糊子集E(k)={L,M,H}，域范圍為[0,1]，隸屬函數如圖8所示。

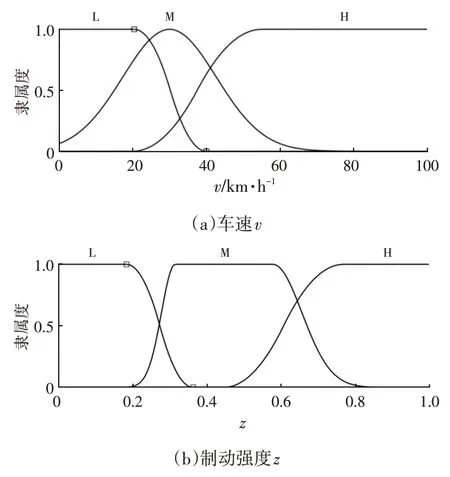
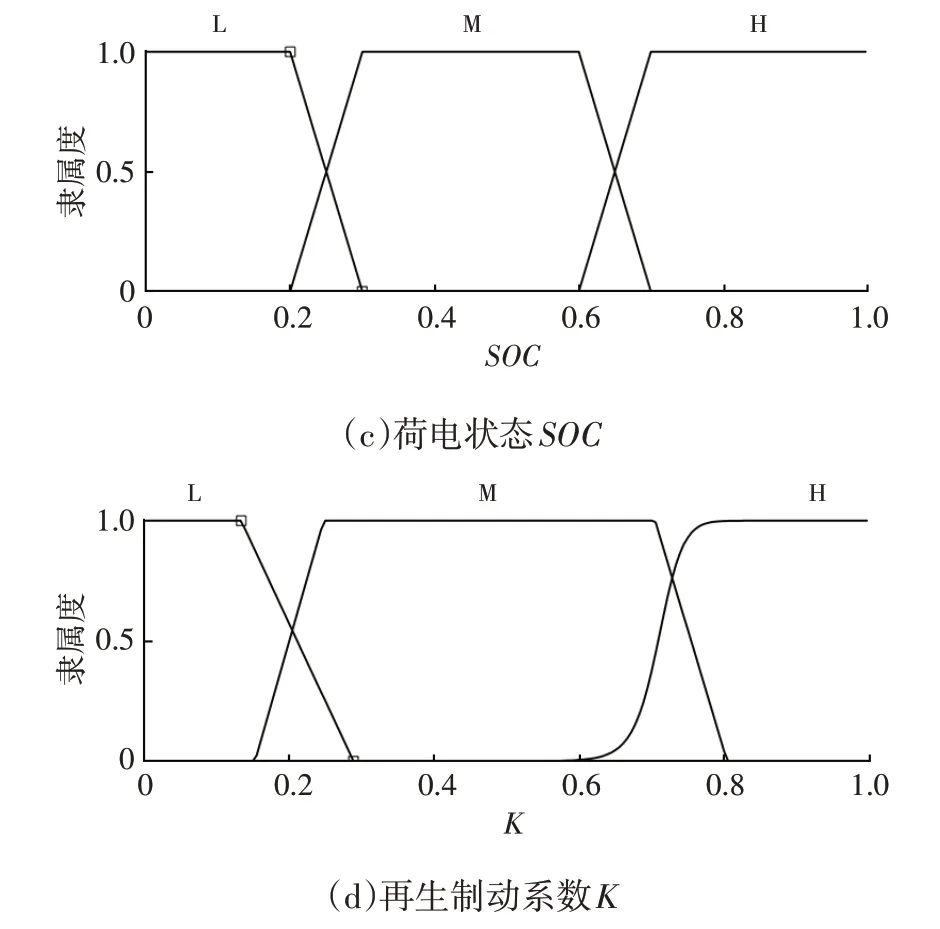
圖8 隸屬函數

通過模糊控制器得到車速v、制動強度z、電池SOC以及再生制動系數K之間的關系如圖9所示。

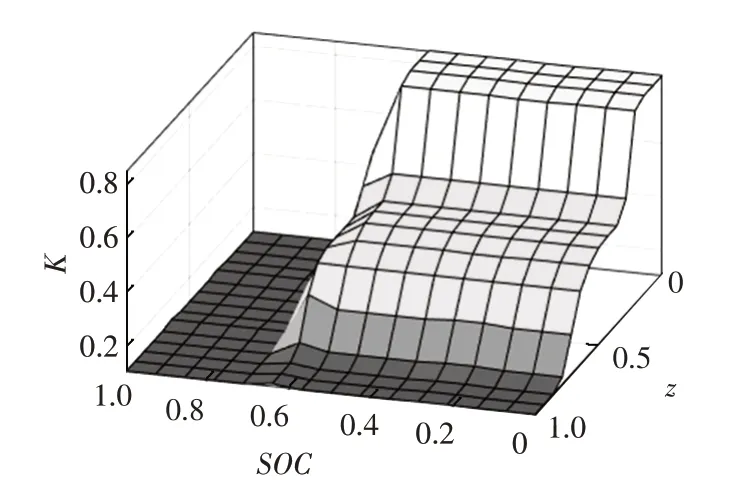
圖9 再生制動系數隨速度、制動強度、SOC的變化曲線

5 仿真結果與分析

5.1 仿真模型的搭建

根據本文所提出的再生制動控制策略，在MATLAB/Simulink環境下搭建基于模糊控制的再生制動模型。為了確保仿真結果的準確性，本文搭建了前向仿真模型和后向仿真模型，如圖10、圖11所示。而在進行電動汽車的仿真計算時，采用ADVISOR中的混合仿真方法，即以后向仿真為主，前向仿真為輔。

圖10和圖11中的模糊邏輯控制策略模型如圖12所示，前、后軸制動力分配子模塊模型如圖13所示。

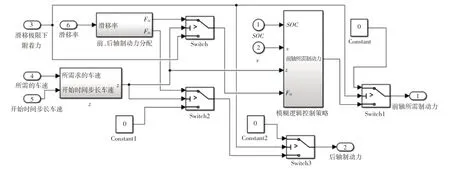
圖11 后向路徑模糊控制制動力分配模型

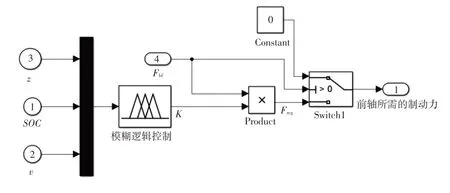
圖12 模糊邏輯控制策略模型

5.2 仿真參數和工況的設置

本文仿真中的純電動汽車相關參數如表1所示。仿真中采用美國城市道路循環工況CYC_UDDS，循環工況基本參數如表2所示。

5.3 仿真結果與分析

把該模型嵌入到ADVISOR2002仿真環境中，并在CYC_UDDS循環工況下驗證模型在電動汽車再生制動系統中的效果。運行ADVISOR2002后，將自帶的控制策略與本文提出的改進策略進行對比，結果如圖14所示。在CYC_UDDS循環工況下汽車制動過程中前、后懸架非簧載質量位移如圖15所示。由圖14可以看出，在CYC_UDDS循環工況結束時，采用本文提出的基于動態軸荷的純電動車再生制動策略時電池SOC減少26%，采用ADVISOR自帶控制策略時電池SOC減少28%，對比SOC提高7.1%，且改進的控制策略電池SOC下降相對緩慢，提高了純電動汽車的續航里程。

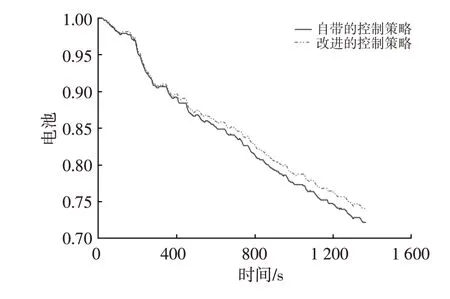
圖14 SOC對比曲線模型

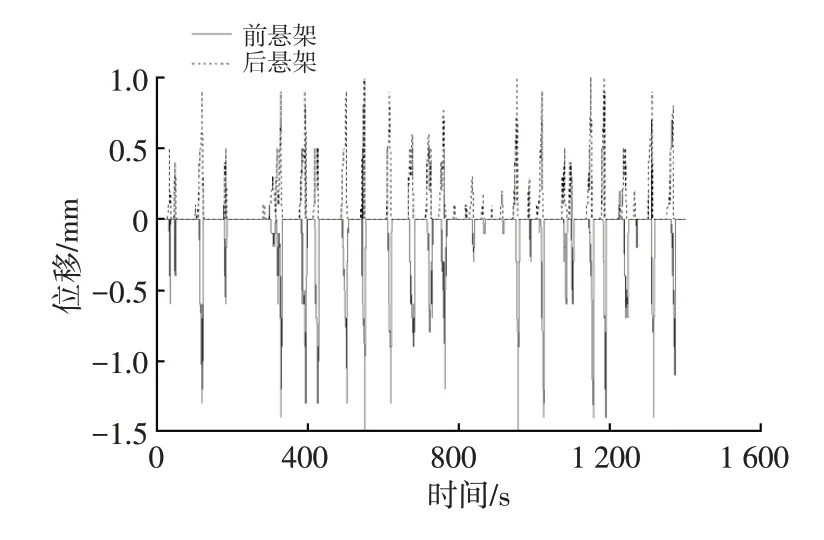
圖15 前、后懸架非簧載質量位移

6 結束語

本文通過對再生制動的研究，針對現有制動策略的不足，考慮到汽車制動時懸架非線性位移造成的軸荷轉移，結合模糊邏輯控制提出一種基于動態軸荷的純電動汽車再生制動策略。利用ADVISOR仿真軟件將軟件自帶的控制策略與本文所提出的控制策略進行對比分析，結果表明，在CYC_UDDS循環工況下，本文提出的基于動態軸荷的純電動車再生制動策略SOC較ADVISOR自帶的控制策略剩余SOC提高7.1%，表明本文提出的控制策略能夠有效提高續駛里程。