三階導及其幾何意義及在高考中的應用

謝朝

【摘要】三階及以上的導數稱為高階導，高階求導在資料中很常見，最明顯的就是泰勒級數.眾所周知，一階導的幾何意義是斜率，可以表示增減，二階導的幾何意義是一階導的斜率，可以表示凹凸，對于三階導的幾何意義，本文將做一些直觀說明，并進一步得出偏移不等式結論，以及本結論在高考中的巨大作用.

【關鍵詞】二階導;琴生不等式;三階導;幾何意義;偏移不等式;對數平均;高考

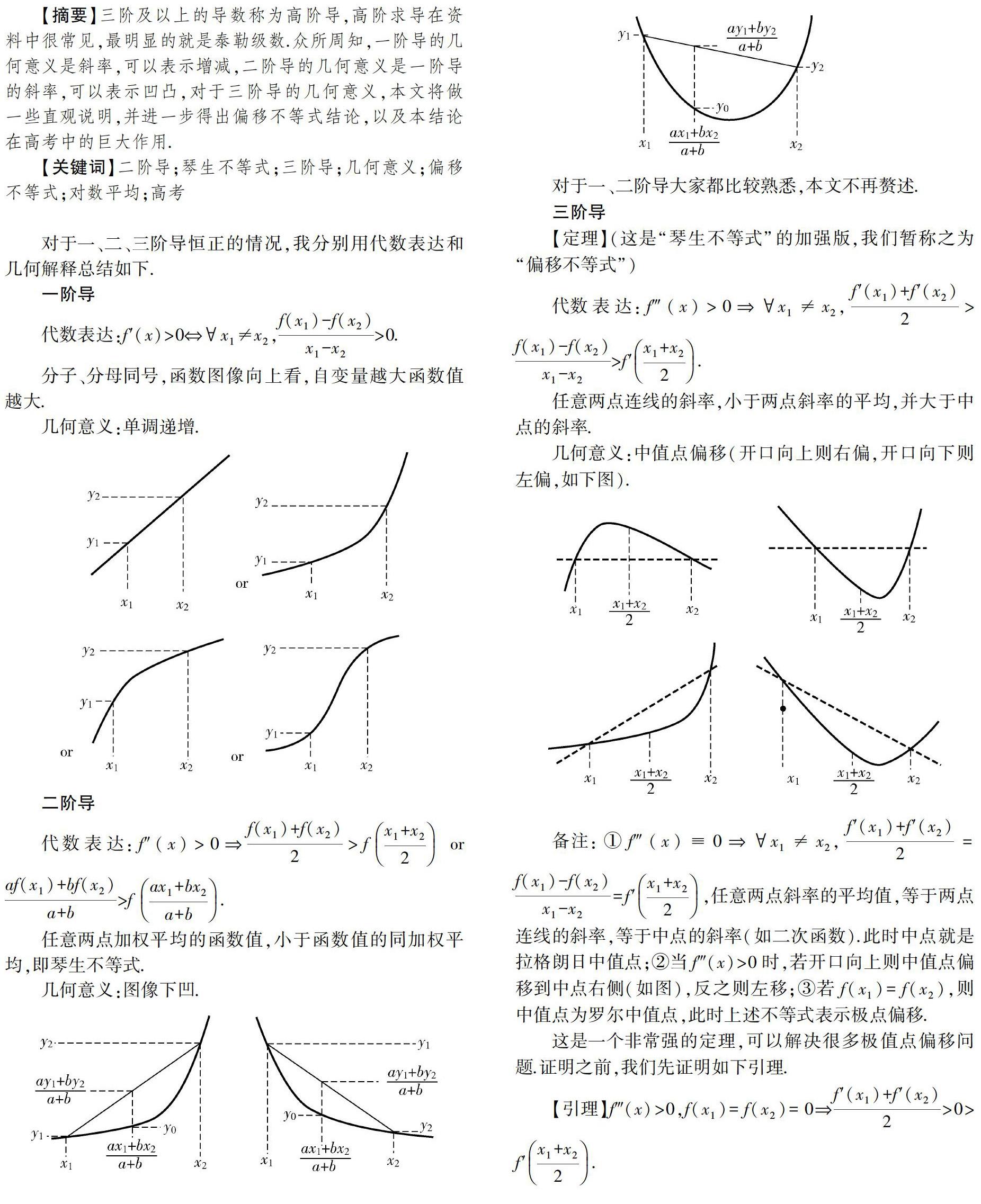
對于一、二、三階導恒正的情況，我分別用代數表達和幾何解釋總結如下.

以上問題除例3都是高考中的壓軸題，但都可用“偏移不等式”秒殺，類似的題目很多，由于篇幅問題，本文就不一一講解.另外，本定理用泰勒展開也很容易證明.留給讀者繼續研究.

【參考文獻】

[1]蔡德華.淺談高考導數壓軸題中的優化運算技巧[J].數學通訊，2019（1）：39-43.

[2]尤新建.巧妙構造輔助函數發展數學核心素養“導數的應用”微專題教學設計[J].數學通訊，2018（12）：31-33.

[3]李寧.與極值點有關的多元最值問題的解題策略[J].數學通訊，2019（2）：1-4.

[4]柏慶昆，李思念.一道導數壓軸題的“溯源”與“深延”改編[J].數學通訊，2019（16）：42-44.