葉片疲勞壽命神經(jīng)網(wǎng)絡(luò)近似計算模型數(shù)值實驗

王 雷, 陸金桂, 李樂為

(1.南京工業(yè)大學(xué)機械與動力工程學(xué)院,南京211800;2.南瑞集團有限公司,南京210061)

風(fēng)力機葉片是風(fēng)力發(fā)電設(shè)備的關(guān)鍵部件,不僅直接影響風(fēng)力發(fā)電設(shè)備的效率,還影響風(fēng)力發(fā)電設(shè)備的成本.開展風(fēng)力機葉片優(yōu)化設(shè)計研究[1]對于促進風(fēng)力發(fā)電設(shè)備的發(fā)展具有十分重要的意義.風(fēng)力機葉片的使用壽命很大程度上取決于疲勞壽命.風(fēng)力機葉片的疲勞研究包含環(huán)境、載荷、材料、結(jié)構(gòu)等方面,涉及動力學(xué)、結(jié)構(gòu)力學(xué)、材料力學(xué)、疲勞理論等多學(xué)科.我國缺少大型風(fēng)力機葉片疲勞壽命實測疲勞應(yīng)力譜.國內(nèi)外針對風(fēng)力機葉片的疲勞壽命等性能分析提出了較多估算方法[2-6],不過估算結(jié)果和實際還存在一定的差異,這需要進一步研究損傷機理和計算模型.目前,復(fù)合材料的計算理論主要有疲勞損傷累積理論和S-N曲線[7-8].李德源等[9]介紹了玻璃鋼材料的疲勞破壞過程、破壞準(zhǔn)則,運用片條理論分析了影響風(fēng)力機葉片疲勞壽命的氣動載荷分布,采用有限元模態(tài)疊加法計算了葉片應(yīng)力,運用線性疲勞損傷累積法則提出了一種玻璃鋼葉片安全壽命估計方法.研究表明,線性疲勞損傷理論對于采用復(fù)合材料的風(fēng)力機葉片疲勞壽命的預(yù)測效果不理想.米良等[10]提出一種將非齊次泊松隨機過程函數(shù)與伴隨損傷理論相結(jié)合來估算零部件疲勞壽命的方法,此方法為風(fēng)力機葉片疲勞壽命計算提供新的思路.

風(fēng)力機葉片疲勞壽命利用有限元分析計算獲得時,優(yōu)化迭代過程需要反復(fù)進行計算,計算量巨大.在風(fēng)力機葉片性能計算研究上,已有文獻借助神經(jīng)網(wǎng)絡(luò)建立近似計算模型.多層神經(jīng)網(wǎng)絡(luò)通過自我學(xué)習(xí)調(diào)節(jié)網(wǎng)絡(luò)模型參數(shù),對于解決復(fù)雜、非線性計算分析具有優(yōu)勢[11].Wang等[12]將神經(jīng)網(wǎng)絡(luò)應(yīng)用于風(fēng)力機葉片結(jié)構(gòu)近似分析模型的建立,并運用粒子群算法進行優(yōu)化模型參數(shù),通過實例驗證了基于粒子群優(yōu)化算法的神經(jīng)網(wǎng)絡(luò)模型風(fēng)力機葉片結(jié)構(gòu)近似分析方法的可行性.

本工作借鑒結(jié)構(gòu)優(yōu)化設(shè)計領(lǐng)域的結(jié)構(gòu)近似分析技術(shù)的思路[13],探討風(fēng)力機葉片疲勞壽命近似計算方法,建立葉片疲勞壽命神經(jīng)網(wǎng)絡(luò)近似計算模型,進行葉片疲勞壽命性能計算,進一步開展風(fēng)力機葉片疲勞壽命神經(jīng)網(wǎng)絡(luò)近似計算模型的數(shù)值實驗,探討提高計算值精度的因素.本工作研究的風(fēng)力機葉片疲勞壽命性能近似計算方法計算過程相對簡單,計算結(jié)果相對可靠,為風(fēng)力機葉片疲勞壽命性能計算提供了一種新的計算手段.

1 模型

陸金桂等[14]對多層神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)近似進行了理論分析,從理論上證明基于多層神經(jīng)網(wǎng)絡(luò)的風(fēng)力機葉片性能近似計算的可行性.通過運用Kolmogorov多層神經(jīng)網(wǎng)絡(luò)映射存在定理從理論上證明了三層神經(jīng)網(wǎng)絡(luò)可用來描述任一彈性結(jié)構(gòu)的應(yīng)力、位移等量和結(jié)構(gòu)設(shè)計變量之間的映射關(guān)系,即假設(shè)X是任一彈性結(jié)構(gòu)的n個設(shè)計變量集,Y是該結(jié)構(gòu)的m個應(yīng)力等性能集,則必定存在一個輸入層(輸入量為X,有n個神經(jīng)元)、隱含層(有2n+1個神經(jīng)元)和輸出層(輸出量為Y,有m個神經(jīng)元)的三層神經(jīng)網(wǎng)絡(luò),該神經(jīng)網(wǎng)絡(luò)可用來精確表達結(jié)構(gòu)的Y與X之間的映射關(guān)系.基于以上神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)近似理論,對于風(fēng)力機葉片結(jié)構(gòu)近似分析問題,我們提出將風(fēng)力機葉片作為彈性結(jié)構(gòu)的特例,風(fēng)力機葉片設(shè)計參數(shù)作為結(jié)構(gòu)設(shè)計變量,風(fēng)力機葉片疲勞壽命性能作為結(jié)構(gòu)的性能,進行有關(guān)風(fēng)力機葉片疲勞壽命性能神經(jīng)網(wǎng)絡(luò)近似計算的推論.

推論假設(shè)X是風(fēng)力機葉片的n個設(shè)計變量集,Y是該風(fēng)力機葉片的m個應(yīng)力等性能集,則必定存在一個輸入層(輸入量為X,有n個神經(jīng)元)、隱含層(有2n+1個神經(jīng)元)、輸出層(輸出量為Y,有m個神經(jīng)元)的三層神經(jīng)網(wǎng)絡(luò),該神經(jīng)網(wǎng)絡(luò)可用來精確表達風(fēng)力機葉片的Y與X之間的映射關(guān)系.

根據(jù)上述推論只要利用三層神經(jīng)網(wǎng)絡(luò)來描述風(fēng)力機葉片的疲勞壽命性能和風(fēng)力機葉片設(shè)計變量之間復(fù)雜的映射關(guān)系,就可利用該三層神經(jīng)網(wǎng)絡(luò)建立風(fēng)力機葉片疲勞壽命性能的近似計算模型.

多層神經(jīng)網(wǎng)絡(luò)具有較強的自學(xué)習(xí)、自適應(yīng)的能力和并行處理能力,對解決大規(guī)模、復(fù)雜問題效果比較好.多層神經(jīng)網(wǎng)絡(luò)使用誤差逆?zhèn)鞑ニ惴ㄟM行數(shù)據(jù)鍛煉,其最小使用基元為神經(jīng)元.神經(jīng)元的特性及差異化神經(jīng)元之間的特有的相接方式?jīng)Q定了神經(jīng)網(wǎng)絡(luò)的特性.神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)中除了輸入、輸出層,還包括隱含層,每層次之間用權(quán)值連接且無任何耦合.

在神經(jīng)網(wǎng)絡(luò)的風(fēng)力機葉片疲勞壽命的近似計算中,關(guān)鍵是建立風(fēng)力機葉片疲勞壽命和風(fēng)力機葉片設(shè)計變量之間的全局性映射的神經(jīng)網(wǎng)絡(luò)模型.確定葉片疲勞壽命近似計算的神經(jīng)網(wǎng)絡(luò)的輸入和輸出參數(shù)后,就可確定風(fēng)力機葉片疲勞壽命近似計算的神經(jīng)網(wǎng)絡(luò)模型結(jié)構(gòu).在風(fēng)力機葉片的設(shè)計參數(shù)中,選擇對風(fēng)力機疲勞壽命性能影響比較大的設(shè)計參數(shù)作為神經(jīng)網(wǎng)絡(luò)的輸入,疲勞壽命性能作為神經(jīng)網(wǎng)絡(luò)的輸出.利用神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)算法對由風(fēng)力機葉片疲勞壽命性能和風(fēng)力機葉片設(shè)計變量參數(shù)構(gòu)成的樣本集進行學(xué)習(xí).由于風(fēng)力機葉片樣本集蘊涵了風(fēng)力機葉片疲勞壽命性能和風(fēng)力機葉片設(shè)計變量參數(shù)映射關(guān)系,通過神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)算法學(xué)習(xí)后就可以建立風(fēng)力機葉片疲勞壽命性能和風(fēng)力機葉片設(shè)計變量之間的全局性模型.

本工作建立的風(fēng)力機葉片疲勞壽命神經(jīng)網(wǎng)絡(luò)近似計算模型如圖1所示.其中輸入層神經(jīng)單元取n個,隱含層數(shù)為1,隱含層神經(jīng)元取2n+1個,輸出層是風(fēng)力機葉片的疲勞壽命.

圖1 風(fēng)力機葉片疲勞壽命近似計算的神經(jīng)網(wǎng)絡(luò)模型Fig.1 Neural network model for approximate calculation of fatigue life of wind turbine blades

2 近似計算應(yīng)用

根據(jù)圖1建立風(fēng)力機葉片疲勞壽命近似計算神經(jīng)網(wǎng)絡(luò)模型進行風(fēng)力機葉片疲勞壽命計算,選擇風(fēng)機葉片的弦長、厚度及載荷作為神經(jīng)網(wǎng)絡(luò)的輸入變量,取值范圍見表1.選出21組數(shù)據(jù),利用有限元分析軟件ANSYS計算數(shù)據(jù)對應(yīng)的風(fēng)力機葉片疲勞壽命性能數(shù)據(jù),構(gòu)造計算實例中風(fēng)力機葉片疲勞壽命近似計算神經(jīng)網(wǎng)絡(luò)模型建立需要的樣本數(shù)據(jù).在風(fēng)力機葉片疲勞壽命性能近似計算實例中,選取其中15個樣本建立風(fēng)力機葉片疲勞壽命近似計算的神經(jīng)網(wǎng)絡(luò)模型,其余的6組數(shù)據(jù)用來進行葉片疲勞壽命的近似計算結(jié)果的對比.

表1 變量取值范圍Table 1 Range of variables

風(fēng)力機葉片疲勞壽命近似計算的神經(jīng)網(wǎng)絡(luò)模型的輸入層單元數(shù)目為3,輸出層單元為1,隱含層神經(jīng)網(wǎng)絡(luò)單元數(shù)目為8.風(fēng)力機葉片疲勞壽命神經(jīng)網(wǎng)絡(luò)模型的學(xué)習(xí)過程采用反向傳播學(xué)習(xí)算法.神經(jīng)網(wǎng)絡(luò)模型學(xué)習(xí)過程中學(xué)習(xí)率參數(shù)為0.9,經(jīng)過4 500次學(xué)習(xí),獲得了風(fēng)力機葉片疲勞壽命,結(jié)果如表2所示.表2中的準(zhǔn)確值是利用有限元分析在設(shè)計參數(shù)條件下計算獲得的葉片疲勞壽命.

表2 葉片疲勞壽命的近似計算結(jié)果Table 2 Approximate results of fatigue life for blade

由表2可知,疲勞壽命的最大相對誤差為14.83%,最小相對誤差僅為0.65%,平均相對誤差為5.72%.除1個設(shè)計點數(shù)據(jù)的近似計算相對誤差較大外,其他設(shè)計的相對誤差都在7.3%以內(nèi).計算結(jié)果初步驗證了基于神經(jīng)網(wǎng)絡(luò)的風(fēng)力機葉片疲勞壽命近似計算模型對于計算葉片疲勞壽命具有一定的可行性.

3 數(shù)值實驗

風(fēng)力機葉片疲勞壽命近似計算的神經(jīng)網(wǎng)絡(luò)模型直接影響風(fēng)力機葉片疲勞壽命近似計算方法的準(zhǔn)確性.考慮到風(fēng)力機葉片疲勞壽命近似計算的神經(jīng)網(wǎng)絡(luò)模型與反映風(fēng)力機葉片性能的樣本[15]、神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)、樣本學(xué)習(xí)有關(guān),本工作從學(xué)習(xí)樣本數(shù)、神經(jīng)網(wǎng)絡(luò)隱含層節(jié)點數(shù)、學(xué)習(xí)精度等方面進行數(shù)值實驗研究.采用有限元計算出風(fēng)力機葉片的疲勞壽命的實際值,利用風(fēng)力機葉片設(shè)計參數(shù)和計算獲得風(fēng)力機疲勞壽命的構(gòu)造樣本.

3.1 學(xué)習(xí)樣本

本工作選取了7種不同數(shù)目的樣本進行實驗.實驗1至實驗7選取的樣本數(shù)依次為5,8,10,12,14,16,18,同時,選擇其他6組數(shù)據(jù)進行對比.實驗結(jié)果如表3～6所示,其中實際值是利用有限元分析在設(shè)計參數(shù)條件下計算獲得的葉片疲勞壽命.

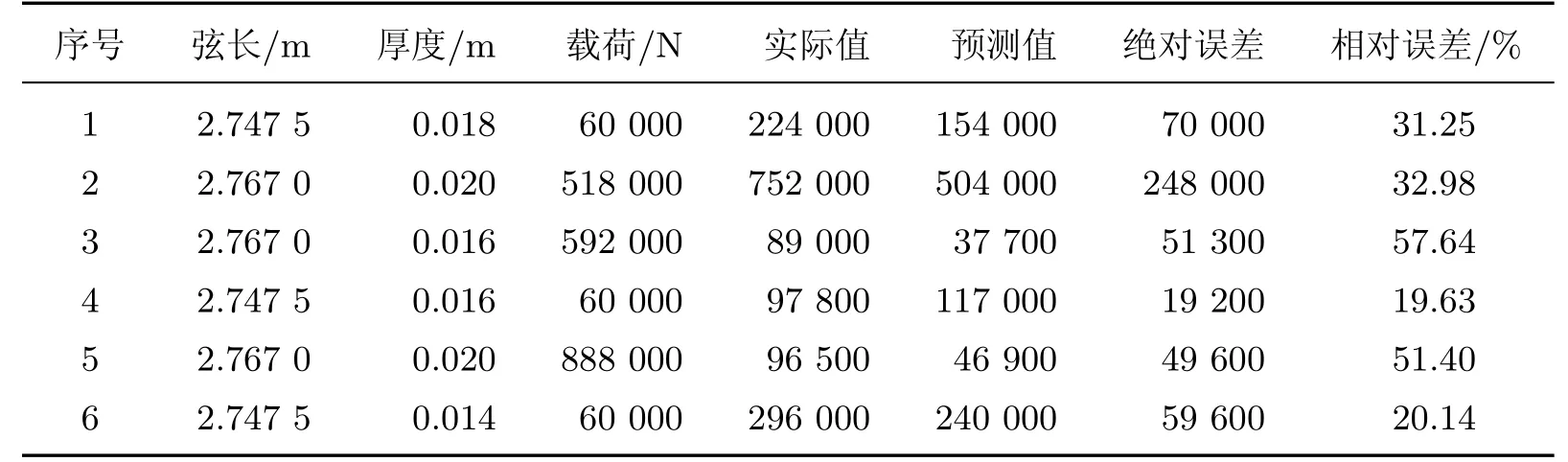
表3 疲勞壽命實驗1結(jié)果Table 3 Results of fatigue life for experiment 1

表4 疲勞壽命實驗2和3結(jié)果Table 4 Results of fatigue life for experiments 2 and 3

表5 風(fēng)力機葉片疲勞壽命實驗4和5結(jié)果Table 5 Results of fatigue life for experiments 4 and 5

表6 疲勞壽命實驗6和7結(jié)果Table 6 Results of fatigue life for experiments 6 and 7

根據(jù)風(fēng)力機葉片疲勞壽命性能近似計算的7個實驗數(shù)據(jù),可以得到學(xué)習(xí)樣本數(shù)量與近似計算結(jié)果誤差關(guān)系,如圖2(a)所示.從圖中可以發(fā)現(xiàn),隨著學(xué)習(xí)樣本數(shù)的增加,葉片疲勞壽命平均相對誤差均呈遞減趨勢.因此,在風(fēng)力機葉片疲勞壽命性能近似計算時,應(yīng)適當(dāng)增加神經(jīng)網(wǎng)絡(luò)模型的學(xué)習(xí)樣本數(shù).

3.2 神經(jīng)網(wǎng)絡(luò)隱含層節(jié)點

本工作選取了7種不同的隱含層節(jié)點數(shù)進行實驗.實驗1至實驗7選取的隱含層節(jié)點數(shù)依次為3,4,5,6,7,8,9,同時選擇其他6組數(shù)據(jù)進行對比,結(jié)果如表7～10所示,其中實際值是利用有限元分析在設(shè)計參數(shù)條件下計算獲得的葉片疲勞壽命.

根據(jù)7個實驗數(shù)據(jù)得到神經(jīng)網(wǎng)絡(luò)模型隱含層節(jié)點數(shù)與疲勞壽命近似計算結(jié)果誤差關(guān)系,結(jié)果如圖2(b)所示.從圖中可以發(fā)現(xiàn),隱含層節(jié)點數(shù)為7時,近似計算誤差最小,近似計算精度最高.

圖2 疲勞壽命近似計算誤差結(jié)果Fig.2 Error results of approximate fatigue life

表7 疲勞壽命實驗1結(jié)果Table 7 Results of fatigue life for experiment 1

表8 疲勞壽命實驗2和3結(jié)果Table 8 Results of fatigue life for experiments 2 and 3

表9 疲勞壽命實驗4和5結(jié)果Table 9 Results of fatigue life for experiments 4 and 5

表10 疲勞壽命實驗6和7結(jié)果Table 10 Results of fatigue life for experiments 6 and 7

3.3 學(xué)習(xí)精度

選取7種不同的神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)精度進行實驗.實驗1至實驗7選取的學(xué)習(xí)精度依次為0.1,0.01,0.005,0.001,0.000 5,0.000 1,0.000 01,同時選擇其他6組數(shù)據(jù)進行對比.7個實驗結(jié)果如表11～14所示,其中實際值是利用有限元分析在設(shè)計參數(shù)條件下計算獲得的葉片疲勞壽命.

表11 疲勞壽命實驗1結(jié)果Table 11 Results of fatigue life for experiment 1

根據(jù)7個實驗數(shù)據(jù)得到神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)精度與疲勞壽命近似計算結(jié)果誤差關(guān)系,結(jié)果如圖2(c)所示.從圖中可以發(fā)現(xiàn),隨著神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)精度的增加,葉片疲勞壽命平均相對誤差總體上均呈大致遞減趨勢.在第7個實驗中,學(xué)習(xí)精度繼續(xù)增加時,葉片疲勞壽命平均相對誤差略有增加.本實驗中,學(xué)習(xí)精度為0.000 1時,建立的風(fēng)力機葉片性能近似計算模型的近似計算誤差最小,近似計算精度最高.

表12 疲勞壽命實驗2和3結(jié)果Table 12 Results of fatigue life for experiments 2 and 3

表13 疲勞壽命實驗4和5結(jié)果Table 13 Results of fatigue life for experiments 4 and 5

表14 疲勞壽命實驗6和7結(jié)果Table 14 Results of fatigue life for experiments 6 and 7

4 結(jié)束語

本工作建立了風(fēng)力機葉片疲勞壽命神經(jīng)網(wǎng)絡(luò)近似計算模型,并對風(fēng)力機葉片的疲勞壽命進行了計算.計算結(jié)果表明,基于神經(jīng)網(wǎng)絡(luò)的風(fēng)力機葉片疲勞壽命近似計算模型對于風(fēng)力機葉片疲勞壽命計算具有可行性,為風(fēng)力機葉片疲勞壽命計算提供了一種新的計算手段.

葉片疲勞壽命近似計算模型數(shù)值實驗結(jié)果表明:①隨著學(xué)習(xí)樣本數(shù)的增加,葉片疲勞壽命平均相對誤差均呈遞減趨勢;②隨著神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)精度的增加,葉片疲勞壽命平均相對誤差呈遞減趨勢;③神經(jīng)網(wǎng)絡(luò)模型的隱含層節(jié)點數(shù)一般取2n+1(n表示輸入單元數(shù)),本工作中隱含層單元數(shù)取7時,計算誤差最小.因此,進行風(fēng)力機葉片神經(jīng)網(wǎng)絡(luò)疲勞壽命近似計算時,應(yīng)適當(dāng)?shù)卦黾訉W(xué)習(xí)樣本數(shù),當(dāng)學(xué)習(xí)精度取0.000 1,隱含層單元數(shù)取2n+1(n表示輸入單元數(shù))時,計算結(jié)果較為理想.