基于平行因子分析的欠定混合矩陣估計算法
王少波,郭 英,眭 萍,李紅光,楊 鑫
(空軍工程大學信息與導航學院, 陜西 西安 710077)
0 引言
盲源分離是指從觀測到的多源混合信號中分離并恢復出相對獨立的源信號的過程[1]。盲源分離是現代信號處理的重要前沿研究領域之一,已經在通信、語音處理、機械故障分析、圖像處理、生物醫學、雷達及經濟數據分析等領域得到廣泛應用[2-4]。
盲源信號分離技術根據源信號數目和混合信號數目之間的關系可以分為:超定、正定和欠定。超定即觀測信號數目大于源信號數目,正定即觀測信號數目等于源信號數目,欠定即觀測信號數目小于源信號數目,其分別對應著不同的解決方法,目前解決超定、正定盲源分離的方法[5]已經相當成熟,而欠定盲分離問題的解決方法還有待進一步的研究。“兩步法”是近年來解決欠定盲源分離問題的一個有效方法,即首先估計混合矩陣,然后在混合矩陣已知的基礎上恢復源信號。估計混合矩陣的精度將直接影響分離信號的質量,因此混合矩陣估計算法非常關鍵。
欠定條件下混合矩陣的估計,主要采用稀疏聚類方法[6-8]和張量分解法[9-13]。文獻[8]選擇時頻域做為稀疏變換域,通過計算接收混合信號時頻比的方差來檢測單源區域,再利用k-均值聚類來完成混合矩陣的估計。基于稀疏聚類的混合矩陣估計方法,計算相對簡單,估計精度較高,但是需要滿足一定的稀疏條件,這限制了該方法的應用范圍。文獻[9]將壓縮感知理論與平行因子分析相結合,實現了欠定盲源分離及DOA估計,但其只適用于具有特殊表示形式的源信號。文獻[10]和文獻[12]將平行因子分析應用到盲源分離問題中,將混合矩陣的估計問題轉化為張量分解問題,該方法提高了估計的準確性和魯棒性,但是進行CP分解的ALS算法對初值敏感且容易陷入局部極值,運算時間較長。文獻[13]引入塔克分解先把張量壓縮為較低維的核張量,然后運用交替最小二乘對核張量進行標準分解,得到混合矩陣的估計,減少了運算時間,但是初值敏感問題依然存在。基于張量分解的估計算法,克服了稀疏聚類算法稀疏性要求,通常需要利用信號的高階統計量構造張量,將混合矩陣的估計問題轉化為張量分解問題,適用于信源相互獨立并且非高斯分布的情況,精度較高,但是算法的計算量較大,運算時間長,且對初值敏感,容易陷入局部收斂。目前研究一種有效的欠定條件下混合矩陣估計方法仍是一個技術難點。
針對現有算法在解決非稀疏信號的欠定混合矩陣估計中,存在的計算時間長、初值敏感且容易陷入局部收斂的問題,提出了基于平行因子分析的欠定混合矩陣估計算法。
1 欠定盲源分離模型及張量理論基礎
1.1 欠定盲源分離模型
欠定盲源分離是指在觀測數目小于源信號數目的條件下,從觀測到的多源混合信號中分離并恢復出相對獨立的源信號的過程。圖1為欠定盲源分離系統原理圖。
設M個相互獨立且非高斯分布觀測信號是來自于N個源信號的線性混合,則欠定盲源分離信號模型描述為:
X(t)=AS(t)+N(t)
(1)
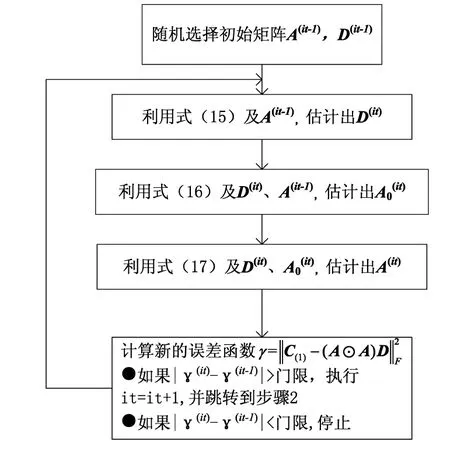
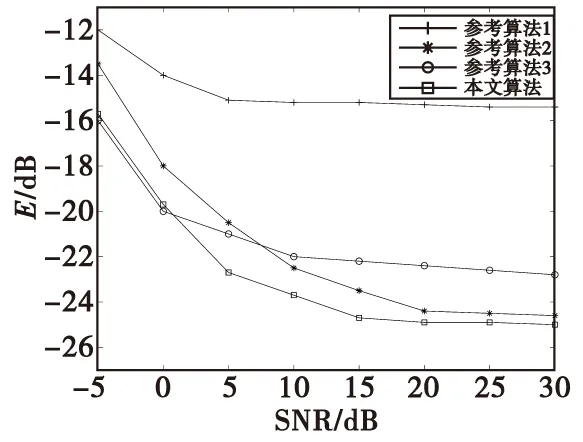
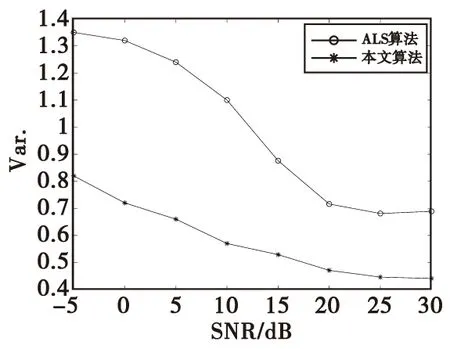
式(1)中,X(t)=[x1(t),x2(t),…,xM(t)]T表示接收的M個觀測信號,S(t)=[s1(t),s2(t),…,sN(t)]T表示輸入的N個未知源信號,M 圖1 欠定盲源分離系統模型Fig.1 Blind source separation system model 一維數組,我們稱之為向量;二維數組,我們稱之為矩陣;三維數組以及多維數組,我們稱之為張量[12]。張量由于其強大的數據分析能力,近年來在數據挖掘、機器學習等領域得到廣泛應用。 下面介紹與張量有關的定義與定理。 定義1(向量的外積)[14]:向量a∈RI1×1與b∈RI2×1的外積是一個I1×I2維的矩陣C,定義為: C=a·b=abT (2) 定義2(秩1張量)[14]:如果三階張量χ等于三個向量的外積,則它的秩為1。 定義3(CP分解)[14]:任何張量χ都允許分解為秩-1張量的總和。在三階張量的情況下,CP分解定義為: (3) 式(3)中,a∈RI1×1,b∈RI2×1,c∈RI3×1,F為張量χ的秩。 定義4(Kronecker積)[14]:I1×I2維矩陣A=[a1,…,aI2]與I3×I4維矩陣B的Kronecker積是一個維的矩陣,并有如下表達式: (4) 定義5(Khatri-Ra積)[12]:I1×I0維矩陣A=[a1,a2,…,aI0] 和I2×I0維矩陣B=[b1,b2,…,bI0]的Khatri-Rao積A⊙B是一個I1I2×I0維的矩陣,并有如下表達式: A⊙B=[a1?b1,…,aI0?bI0] (5) 平行因子分析(PARAFAC)最重要的一個特征就是CP分解是具有唯一性的。它是采用平行因子模型進行數據分析的首要條件。下面給出PARAFAC模型分解唯一性的一個重要定理。 定理1(PARAFAC模型的分解唯一性)[13]:若χ∈RI1×I2×I3是一個具有如式的CP分解張量,其中A∈RI1×F、B∈RI2×F和C∈RI3×F,如果滿足: k(A)+k(B)+k(C)≥2F+2 (6) 則矩陣A,B和C在存在尺度模糊和列模糊的條件下是唯一的(也稱為本質唯一)。 本文利用通信信號的協方差矩陣構造三階張量,將混合矩陣估計問題轉化為了張量分解問題,重點針對現有張量分解算法存在的局部收斂和初始矩陣選擇的問題提出改進,采用非迭代的方法確定交替最小二乘算法的初始迭代矩陣,為了減少運算時間,在迭代過程中采用標準線搜索加速收斂。 本文采用文獻[10]中的方法來構造三階張量,具體方法如下: 對于零均值且互不相關的非平穩實信號,源信號在t時刻的協方差矩陣可表示為: (7) 式(7)中,Dk=E{stst+tk}是對角矩陣,k=1,…,K。為了簡化,先忽略噪聲的影響。解決的問題是在M 可以將矩陣C1,…,Ck按如下方式壓縮為張量C∈M×M×K:(C)ijk=(Ck)ij,i=1,…,M,j=1,…,M,k=1,…,K。通過(D)kf=(Dk)ff定義一個矩陣Dkf,得到: (8) 將其改寫為: (9) 式(9)中,af和df分別代表矩陣A和D的列向量。 張量沿三個方向的切片展開為矩陣,C(1)∈M2×K,C(2)∈KM×M,C(3)∈MK×M: (C(1))(i-1)M+j,k=(C(2))(k-1)K+i,j=(C(3))(j-1)M+k,i=Cijk (10) 根據式(10),張量的三個切片展開矩陣可以寫為 C(1)=(A⊙A)·DT (11) C(2)=(D⊙A)·AT (12) C(3)=(A⊙D)·AT (13) 由定理1知,滿足一定條件,張量的CP分解唯一存在。文獻[10]給出了傳感器數目和源信號數目使CP分解唯一的關系,如表 1所示。 表1 觀測數M與所允許的源信號最大數目Nmax的關系Tab.1 The relationship between the number of observations M and the maximum number Nmaxof source signals 至此,將欠定混合矩陣的估計問題轉化為三階張量的CP分解問題。 作為解決PARAFAC模型的經典算法,ALS算法算法步驟如圖 2所示。 圖2 ALS算法流程Fig.2 The ALS algorithm flowchart 算法通過交替最小二乘誤差γ,來獲得混合矩陣。 (14) 式(14)中,‖·‖F代表F-范數,當矩陣A固定,D的估計值可以由最小二乘結果得到: (15) 式(15)中,(·)+表示廣義逆矩陣。 同理,分別利用式(12)與式(13),通過同樣的方式可得 (16) (17) 由于初始矩陣的選擇對ALS算法的準確性及收斂路徑有比較大的影響,本文采用非迭代的直接三線性分解法確定ALS算法初始矩陣。 直接三線性分解[16]算法是一種非迭代的求解平行因子模型的三維分解方法,但是其精度和可靠性比ALS算法要差,可以作為ALS算法的初始矩陣。 第一步 根據式(11)、式(12)和式(13),分別對C(1)、C(2)和C(3)進行奇異值分解,其中U、V取前F個奇異值矢量,W取前兩個左奇異值矢量。 C(1)=UISIVIU=UI(I×R) (18) C(2)=UJSJVJV=UJ(J×R) (19) C(3)=UKSKVKW=UK(K×2) (20) 第二步 利用式(21)、式(22)構造為樣本矩陣G1、G2。 (21) (22) 式中,wki為矩陣W中的元素,Ck∈RM×M為張量C的第k個切片矩陣。 第三步 使用QZ分解陣G1、G2組成的特征方程,L、M分別為方程的特征向量,可證明矩陣A和D分別可由式(23)、式(24)得到[14]。 G1Lλ2r=G2Lλ1rA0=UL-1 (23) G1Mλ2r=G2Mλ1rA0=VM-1 (24) 至此,通過直接三線性分解得到了粗估的加載矩陣,將其作為ALS算法的初始矩陣,開始迭代。 ALS算法運算時間較長,本文使用標準線搜索加速收斂。 本文采用直接三線性分解粗估混合矩陣,將其作為ALS算法初始矩陣,迭代過程中采用標準的線搜索加速收斂。 線搜索方法首先找到使目標函數減少的反向,然后計算沿著下降方向移動的步長。下降方向可以由各種不同的方法計算,如梯度下降法。 例如在t次迭代,根據算法預測一定的迭代步長ρ,對矩陣A進行更新,可以表示為:A=A+ρΔA。 本文采用的線加速方案為只對矩陣D進行線搜索: D(new)=D(it-2)+RLS(D(it-1)-D(it-2)) (25) 針對矩陣A,利用式(17)采用最小二乘進一步估計。 算法步長的計算應該十分簡單,如果它比相應的迭代需要更多的時間則沒有意義。最簡單的情況是,RLS被賦予固定值(在1.2~1.3之間)[17],或者被設置為(it)1/3[18]。本文的RLS設置為(it)1/3。 具體算法流程: 步驟1 根據直接三線性分解算法粗估加載矩陣A0,D0; 步驟2 利用式(15)和A0估計出D1,利用式(16)和A0及D1估計出A1,令it=2,則A(it-2)=A0,D(it-2)=D0,A(it-1)=A1,D(it-1)=D1; 步驟3 根據線加速公式(25)計算D(new),利用式(17)及A(it-1)D(it-1)計算A(new); 步驟4 分別利用A(new)、D(new)和A(it-1),D(it-1)及式(14)計算誤差函數γ(new)和γ(it-1); 步驟5 若γ(new)<γ(it-1),A(it-1)=A(new),D(it-1)=D(new),γ(it-1)=γ(new);否則,直接執行步驟6; 步驟6 利用式(15)和式(16)及A(it-1),D(it-1);計算得A(it)和D(it): (26) (27) 為說明算法的性能,算法的效果評估采用混合矩陣估計誤差和迭代次數作為指標。 本節通過采用不同調制方式信號來完成欠定條件下混合矩陣估計實驗。 實驗采用4路不同調制方式的輻射源信號:s1為跳頻信號;s2為LFM信號;s3為QPSK信號;s4為FM信號。觀測信號數目設為3,信號采樣點數為4 096,信噪比變化范圍為-5~30 dB,步進為5 dB,每個信噪比處蒙特卡洛仿真實驗100次。 評價混合矩陣估計性能采用歸一化均方誤差: (28) 實驗仿真結果如圖3所示,橫坐標為信噪比,縱坐標為歸一化均方誤差。參考算法1采用K均值聚類算法[19],直接進行迭代估計出混合矩陣。參考算法2采用ALS算法[10],受初始值的選擇及局部收斂的影響,在低信噪比條件下混合矩陣估計性能一般。參考文獻[3]采用的AP聚類方法[20],將每個樣本都視為潛在的聚類中心,通過迭代確定聚類中心。本文算法先用非迭代的方法確定初始矩陣,再進行迭代確定混合矩陣。從圖 3可以看出,直接采用K均值聚類算法,接收陣元信噪比達到5 dB時, 就已達到極限,約為-15.5 dB,信噪比大于5 dB時,信噪比的增加無法提升混合矩陣的估計準確性;采用本文算法、參考算法2以及參考算法3,混合矩陣估計的準確性隨著信噪比的增加而增加,在低信噪比條件下,本文算法估計準確性較參考算法2提升約3 dB,與參考算法3性能接近,在信噪比較高的條件下,本文算法的性能要明顯優于參考算法3,略優于參考算法2。對100次蒙特卡洛實驗得到的歸一化均方誤差求方差,得到仿真結果,如圖4所示,橫坐標為信噪比,縱坐標為100次實驗得到的均方誤差的方差。從圖中可以看出,本文算法均方誤差的方差位于ALS算法減小了約0.5,說明本文算法在估計的穩定性上有了較大的提升。 圖3 均方誤差隨信噪比變化曲線Fig.3 Mean square error with SNR curve 本節通過設定不同的觀測數目與信源數來完成算法迭代次數估計實驗。實驗首先設置觀測數目及信源數,然后隨機生成A和D,進行蒙特卡洛仿真實驗100次,記錄歸一化均方誤差ENMSE達到10 dB時,所需的平均迭代次數。 圖4 均方誤差的方差隨信噪比變化曲線Fig.4 The variance of the mean square error varies with SNR curve 表2列出了兩種算法運行一次的平均迭代次數,從表中可以看出在(M,N)取不同值條件下,本文算法迭代次數上較ALS算法減少約41.4%~84.3%,且混合矩形規模越小,減少幅度越大。 表2 (M,N)取不同值時算法的迭代次數Tab.2 Number of iterations of the algorithm when (M,N) take different values 本文提出了基于平行因子分析的欠定混合矩陣估計算法。該算法利用信號的協方差矩陣構造三階張量,采用直接三線性分解確定交替最小二乘算法的初始迭代矩陣,然后在迭代過程中采用標準線搜索加速收斂,最終實現張量分解得到混合矩陣。仿真實驗表明,該方法不要求信源的稀疏性,較ALS算法估計精度可以提高約3 dB,迭代次數可以減少約41.4%~84.3%,是一種有效的欠定混合矩陣估計算法。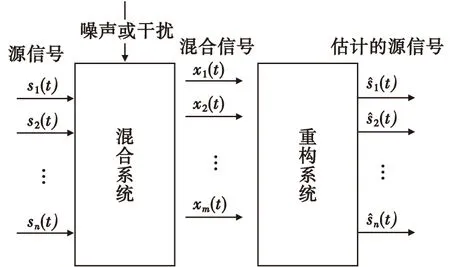
1.2 張量理論基礎
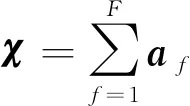
2 基于平行因子分析的欠定混合矩陣估計
2.1 構造張量
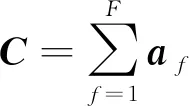

2.2 ALS算法
2.3 直接三線性分解
2.4 算法流程
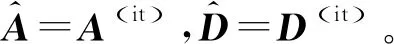
3 仿真實驗與分析
3.1 混合矩陣估計誤差
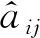
3.2 迭代次數

4 結論

