基于ANM的寬帶非相干子空間DOA估計方法
石 娟,張群飛,毛琳琳,史文濤,王偉東
(1.西北工業大學航海學院,陜西 西安 710072;2.中國科學院聲學研究所,北京 100190)
0 引言
波達方位(Direction of Arrival,DOA)估計是陣列信號處理重要的研究內容之一,其應用涉及雷達、通信、聲納、勘探等眾多工程領域[1-2]。DOA估計方法主要包括子空間分類方法和子空間擬合方法。目前,比較成熟、穩定的DOA估計方法大都是基于陣列的空間譜估計方法,如多重信號分類方法(Multiple Signal Classification,MUSIC)和旋轉不變子空間方法(Estimation of Signal Parameters via Rotational Invariance Techniques,ESPRIT)等,以它們為代表的空間譜方法突破了瑞利限,使測向定位技術實現了飛躍[3]。但這些方法的實現需要大量獨立同分布的測量數據(大快拍數據)。在實際環境中,獲取大快拍數據受到時間的制約,如高速運轉的目標對系統實時性要求很高,尤其在處理超寬帶窄脈沖等短時突發數據時,接收信號經過相干累積后只有小快拍數據乃至單快拍數據,無法直接用常規的DOA估計方法進行方位估計。因此,研究小快拍乃至單快拍的DOA估計便是一種有效解決方案。文獻[4]提出了單快拍下基于匹配跟蹤的ESPRIT的方位估計方法。文獻[5]中提出了單快拍及多快拍下聯合Matrix Pencil 和 ESPRIT的方位估計方法。隨著壓縮感知技術的發展,稀疏重構的思想被用于DOA估計中[6],然而,稀疏重構方法對網格劃分比較敏感,容易造成信號基失配。為了解決信號失配問題, Tang. 等人提出了基于最小原子范數(Atomic Norm Minimization,ANM)的無網格壓縮感知理論[7]。ANM是一種結構優化方法,其基于陣列流型矩陣的范德蒙結構,通過半正定規劃(Semidefinite Programming,SDP)可以構造恢復出所需的Toeplitz矩陣。目前,國內外已有不少基于ANM 的DOA估計的研究,如文獻[8—9],這些方法都是基于窄帶信號DOA估計的研究。
眾所周知,在實際應用中,寬帶信號源大量存在,并且它能夠提供比窄帶更多的信息,有利于目標信號檢測、參數估計和特征提取[10]。目前,寬帶信號處理方法的研究主要基于兩大類[10]:一類是基于非相干合成的寬帶處理方法(Incoherent Signal Subspace Method,ISM),如文獻[11]提出了基于歸一化的克拉美羅界(Cramer-Rao bound, CRB)加權非相干寬帶DOA估計方法;另一類是基于相干合成的寬帶處理方法(Coherent Signal Subspace Method,CSM),如文獻[12]提出了一種基于加權擬合的相干處理的子空間寬帶信號DOA估計方法。然而,這兩種寬帶處理的子空間DOA估計方法的實現都依賴于大快拍數據,無法直接有效的處理小塊拍數據。
本文為了解決寬帶信號在單快拍下的DOA估計失效問題,提出了基于ANM的寬帶非相干子空間DOA估計方法(Atomic Norm Minimization Incoherent Subspace Method,A-ISM)。該方法利用子帶陣列流型矩陣的范德蒙結構,對每個子帶分別進行ANM結構優化,再利用Root-Music算法來估計角度,最后將子帶估計結果的均值作為方位估計結果。
文中(·)T、(·)H分別表示轉置和共軛轉置運算、tr(·)表示矩陣求跡運算、‖·‖為范數運算、‖a‖2表示a的2范數、‖A‖F代表矩陣A的Frobenius范數,E[·]表示期望運算。
1 寬帶信號模型和非相干子空間方法
1.1 寬帶信號模型
假設觀測空間存在K個遠場寬帶信號(θ1,θ2,…,θK)入射到M元均勻線陣(M>K),其中,θk表示第個k信號的入射角,如圖1所示。假設陣列接收的信號不存在相關性,各陣元間噪聲相互獨立,且為平穩、零均值的高斯空間白噪聲,其方差為σ2。
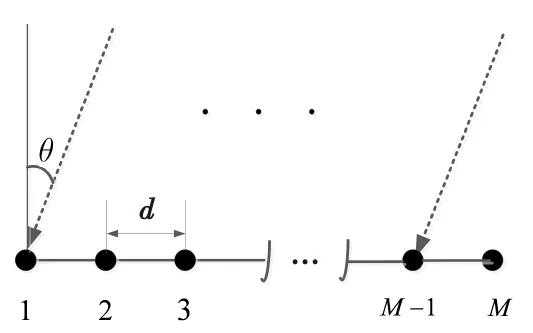
圖1 陣列結構Fig.1 Array structure
文中假設信號源的個數已知,且寬帶信號的工作頻率在[fl,fh]之間,則第m個陣元在第t時刻接收到的數據可以表示為:
(1)
式(1)中,sk和wm分別表示第m陣元接收到來自第k個信號源的信號和噪聲,τm(θk)表示位于θk的目標入射到第m陣元和相對于參考陣元的時延,L代表快拍數。
寬帶信號帶寬為B=fh-fl,將其劃分為N個子頻帶(窄帶),各子頻帶的頻率分別為f0,f1,…,fN-1,則第n個子帶的接收數據為:
Yn=A(fn,θ)Sn+Wn
n=1,2,…,N
(2)
式(2)中,Sn=[s1s2…sK]T∈K×L,Wn∈M×L。為了簡化表示,在下面的章節中A(fn,θ)用An(θ)表示,且An(θ)∈M×K是范德蒙矩陣。第n個子帶的導向矢量矩陣表示為:
An(θ)=[a(fn,θ1)a(fn,θ2) …a(fn,θK)]
(3)
其中,第k個信號在第n頻帶上的導向矢量為:
(4)
式(4)中,d表示陣列陣元間距,c為信號的傳播速度。因此,寬帶信號的的模型可以寫成:
(5)
1.2 非相干子空間方法
基于非相干信號ISM方法是最早出現的寬帶DOA估計方法,主要思路是將寬帶信號劃分為多個子帶,對每個子帶利用信號子空間或噪聲子空間, 求出空間譜或真實信號的根來估計方位角度,最后將各子帶所得結果平均作為最終方位估計結果。
根據寬帶信號的模型,第n個子帶的協方差矩陣為:
(6)
(7)
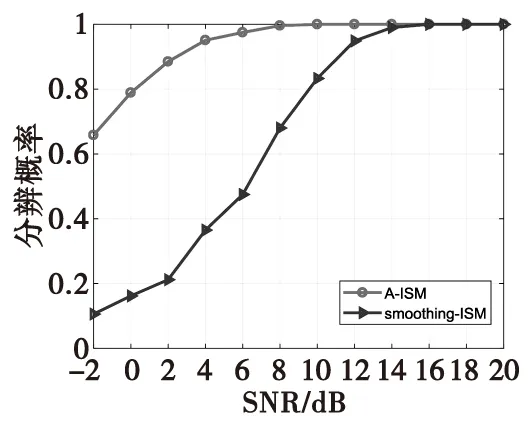
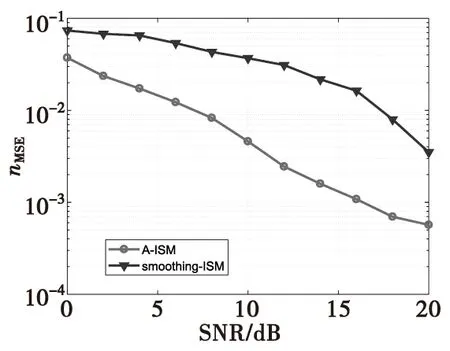
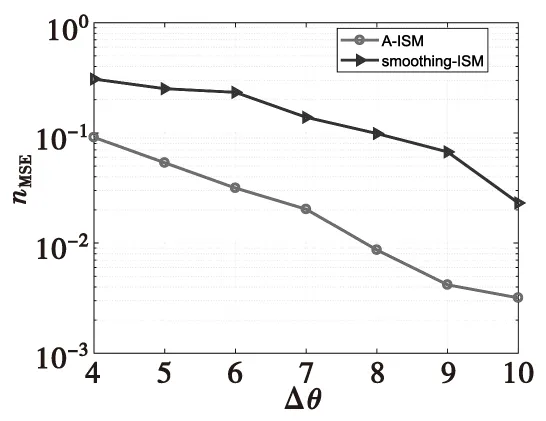
式(7)中,ynl表示第n子帶的第l次快拍數據。當L 圖2 平滑方法原理圖Fig.2 Smoothing method principle structure M元均勻線陣分成相互交錯的P個子陣(P=1+M/2),每個子陣的個數為M/2,第n子帶平滑后的數據可以表示為: (8) 平滑后協方差矩陣表示為: (9) (10) 其中,特征值λi?λg,vi和vg分別代表特征值λi和λg對應特征向量,且信號子空間Us和噪聲子空間Uw可描述為: (11) 在得到噪聲子空間Uw后,將其應用到Root-Music方法中進行DOA估計。首先,Root-Music方法定義為如下一個多項式[13]: (12) 其中 Q(z)=[1z…zM-1]T (13) 由式(12)求出K個接近單位圓的根z1,z2,…,zK。 然后, 根據下式得到第n個子帶的DOA估計角度 (14) 隨后,對N個子帶估計出來的角度求均值,得到最終DOA估計: (15) ISM方法在處理寬帶信號時,應用了窄帶平均思想,并且要求各子帶數據的快拍數必須大于陣元個數,即L>M,否則不能滿足子空間類方法對空間協方差矩陣滿秩的要求。當數據有限,尤其快拍數L=1時,直接應用傳統的ISM方法進行DOA估計時,系統完全不能工作。雖然平滑ISM方法可以估計方位,但是必須以犧牲目標分辨率為代價[14]。針對單快拍下的方位估計,本文提出了基于最小原子范數的寬帶非相干子空間DOA估計方法(A-ISM)。該方法可以直接用單快拍數據,通過ANM構造并會恢復出Toeplitz 矩陣進行DOA估計。 在單快拍L=1條件下,第n子帶接收的數據可表示為: yn=xn+wn= (16) 式(16)中,yn為M×1的向量,xn∈M×1和wn∈M×1分別表示信號向量和噪聲向量。首先考慮無噪聲條件,即式(16)中只包含了與角度有關的信號信息,其可寫成: yn=xn=An(θ)snn=1,2,…,N (17) 原子核定義為: (18) 式(17)表明,xn是An(θ)的線性組合,因此,xn的原子范數可表示成: (19) 根據文獻和式(4)可知,如果信號源是稀疏的,則xn中的sin(θ)就是稀疏的,式(17)就能夠進行稀疏原子分解。求解原子范數最小化是一個NP(Non-Deterministic Polynormial)問題,很難直接求解。而原子范數具有半正定規劃性質(SDP),采取線性半正定規劃方法就能在多項式時間內求解原子范數;同時,由Caratheodory-Toeplitz引理可知,任何半正定Toeplitz矩陣都能進行范德蒙分解[8]。因此,可以將原子范數最小化問題轉化為半正定規劃問題,其可以描述為[8]: (20) 由式(20)可以解出一個最優的向量un=[un1un2…unM]T,用以構造最優的Toeplitz矩陣[7] (21) 式(20)中的半正定的約束,根據舒爾補(Schur Complement)條件,其可等價于[14]: (22) (23) 實際應用中,噪聲總是伴隨著信號存在,因此,式(20)中必須考慮對噪聲作用進行約束。噪聲存在時,ANM的SDP可以重新描述為: (24) 式(24)中,ρ是一個正則化參數,用來調節T(un)的Toeplitz結構與yn中噪聲方差。給定了噪聲方差σ2,ρ可以根據下式計算[6]: (25) 本章以水下被動探測系統為背景,在單快拍下,利用計算機仿真分別從分辨概率、方位估計歸一化均方誤差對A-ISM方法和平滑ISM方法的DOA估計性能進行比較分析。 仿真實驗中均采用16元均勻線陣,目標源個數K=2,工作頻率為3 000~3 100 Hz,子頻帶個數N=3,快拍數L=1。陣元分布均滿足陣元間距為寬帶信號最低頻率fl對應波長的半波長,水聲傳播速度c=1 500 m/s。仿真中利用CVX包解決式(20)和式(24)中的SDP問題。 首先,圖3比較了目標源位于(30° 36°)時,本文所提的A-ISM方法和平滑ISM方法的分辨概率。本次仿真實驗的分辨概率是指在若干次蒙特卡羅實驗中,能夠正確分辨兩個或多個目標的概率。正確分辨需滿足以下條件: (26) 式(26)中,B=arcsin(0.44λ/Md) 。由圖3可以得出,分辨概率為95%時,A-ISM方法需要的信噪比為4 dB,而平滑ISM方法需要的信噪比為12 dB,A-ISM方法相較平滑ISM方法,信噪比提高了8 dB。 圖3 分辨概率與信噪比的關系,L=1,θ=(30° 36°)Fig.3 Probability of resolution versus SNRs,L=1, θ=(30° 36°) 圖4中依然假設目標源位于(30° 36°),給出了A-ISM方法和平滑ISM的方位估計性能隨信噪比的變化情況,且本節的仿真實驗中,方位估計選取歸一化均方誤差(nMSE)作為衡量方位估計誤差的標準,定義為: (27) 圖4 歸一化均方根誤差與信噪比的關系,L=1,θ=(30° 36°)Fig.4 nMSE of DOA versus SNRs,L=1, θ=(30° 36°) 圖5和圖6比較了兩種方法在不同信噪比下,歸一化均方誤差隨著兩目標夾角Δθ的變化情況,以此來衡量方法的方位估計性能。從圖中可以看出,平滑ISM方法與A-ISM方法的歸一化均方誤差曲線存在一定的差距,后者估計性能更優。再比較圖5和圖6,隨著信噪比的提高,兩種方法的歸一化均方誤差均有減小,但相較平滑ISM方法,A-ISM方法的歸一化均方誤差依舊較小,表現出較優的估計性能。 圖5 歸一化均方誤差與的目標夾角關系,SNR=10 dB,L=1Fig.5 nMSE of DOA versus the DOA separation,L=1 圖6 歸一化均方誤差與的目標夾角關系, SNR=15 dB,L=1Fig.6 nMSE of DOA versus the DOA separation,SNR=15dB,L=1 本文提出了基于ANM的寬帶非相干子空間DOA估計方法(A-ISM)。該方法通過各子帶進行ANM優化處理,恢復出最優的Toeplitz矩陣,該矩陣經過特征分解能準確區分信號子空間和噪聲子空間,再結合Root-Music算法,最終得到誤差較小的估計角度。該方法不僅解決了單快拍下經典寬帶信號DOA估計方法失效問題,而且提高了方位估計性能。仿真結果驗證了所提DOA估計方法的正確性和有效性。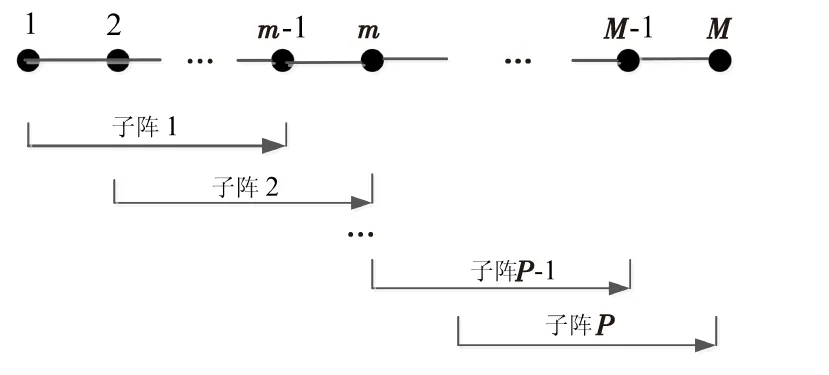
2 基于ANM的寬帶非相干子空間方位估計方法
An(θ)sn+wnn=1,2,…,N
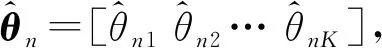
3 仿真與分析

4 結論

