MEMS陀螺儀加速參數退化的可靠度評估

劉 吉，于麗霞,武錦輝

(1.中北大學信息與通信工程學院，山西 太原030051；2.中北大學儀器與電子學院 ，山西 太原030051)

0 引言

MEMS陀螺儀廣泛應用于航空、航天、國防等領域，其在應用過程中的質量和可靠性要求越來越高，而衡量器件可靠性重要指標的可靠度評估問題備受關注，尤其是如何采用高效準確的可靠性試驗與評估方法得到符合MEMS陀螺儀原理、敏感結構尺寸、加工工藝及工作規律的可靠度指標[1-3]。

以失效時間為依據的可靠度評估方法只利用了樣本的正常和失效兩種狀態，忽視了退化過程的微觀變化；基于性能退化的可靠度評估方法試驗時間足夠長，試驗樣本數量足夠多，否則對樣本可靠度做統計推斷的精度較差[4-5]。針對此問題，本文提出了MEMS陀螺儀加速參數退化的可靠度評估方法。

1 MEMS陀螺儀結構及退化評估方法

本文研究的MEMS陀螺儀基于靜電驅動、電容檢測原理，結構如圖1所示，其中角速率敏感元件是核心部分，主要由驅動模塊、微結構和檢測模塊組成。描述MEMS陀螺儀特性的參數有很多，其中零偏易于穩定測量又能客觀反映樣本的工作狀態，是應用領域關注的最基本參數，因此選擇零偏作為加速退化試驗的特征參數[6]。

圖1 MEMS陀螺儀組成結構框圖Fig.1 Principle diagram of MEMS gyroscope

MEMS陀螺儀在實際應用環境中常伴隨高溫、溫變、瞬態高溫等惡劣環境，而制作芯片的硅材料受溫度變化影響顯著, 不但結構尺寸發生變化，而且彈性模量、殘余應力等性能也會變化，從而導致器件失效，造成測試彈體信息的精確度下降。為快速得到樣本失效敏感參數退化量與溫度的關系，采用加速恒定步進應力的加載方式，最高應力不能大于該樣本結構材料、制造工藝所能承受的極限應力，且保證不同應力下退化失效機理一致。依據阿倫尼斯模型，確定尺度參數與應力的關系，利用試驗數據計算加速參數，從而得到可靠度指標[7-8]。

2 加速參數退化的可靠度評估方法

加速參數退化可靠度評估的核心是合理建立參數退化模型和相關參數的加速模型。建立參數退化模型包括基于退化軌跡擬合和基于退化量分布擬合，其流程如圖2和圖3所示[9-10]。

圖2 加速退化軌跡評估流程Fig.2 Assessment process accelerated degradation distribution

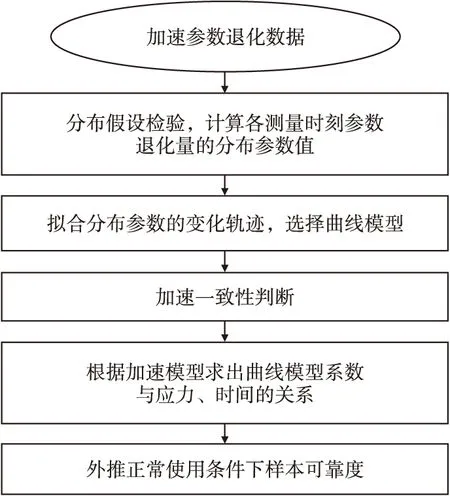
圖3 加速退化量分布評估流程Fig.3 Assessment process accelerated degradation distribution

基于退化軌跡擬合的方法根據各樣本的加速參數退化趨勢，選擇適當的退化軌跡模型；根據應用需求，選擇退化失效閾值，確定偽失效時間；對偽失效時間分布假設檢驗，選擇最恰當的分布形式，估計分布參數；通過加速一致性判斷，選擇加速模型求出分布參數與應力的關系；外推正常使用條件下樣本的總體參數及可靠度參量函數。

基于退化量分布擬合的方法是對多個樣本在不同測量時刻的退化量分布規律進行建模，能夠反映出參數退化量的統計特征隨時間的變化規律。其主要思路是對各個測量時刻的退化數據分布假設檢驗，計算各個時刻參數退化量的分布參數估計值；擬合分布參數隨時間的變化規律，選擇曲線模型，求出各應力水平下曲線模型系數；通過加速一致性判斷，選擇加速模型，求出曲線模型與應力水平的關系；根據加速方程，求正常應力下滿足退化失效閾值時樣本的分布參數隨時間的函數關系，從而得到可靠度函數。

3 MEMS陀螺儀加速參數退化可靠度評估驗證實驗

本文對15個MEMS陀螺儀樣本開展了加速參數退化試驗，圖4是根據樣本在三組高溫應力(T=70 ℃,100 ℃,120 ℃)下加速退化試驗中零偏值變化情況繪制的退化軌跡，結合應用背景，假設該樣本的退化失效閾值是增加3% (即Df=3)，正常工作溫度為T0=25 ℃。應用上述加速參數退化的可靠度評估方法對其進行可靠度評估。

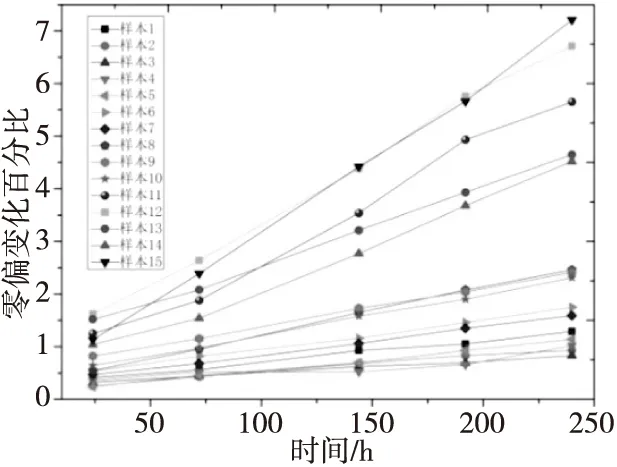
圖4 不同應力下樣本的參數退化軌跡Fig.4 Parameter degradation traces of samples under different stresses

3.1 基于退化軌跡的擬合方法

根據圖4估計所有應力水平下所有樣本的退化軌跡模型參數，外推每個樣本到達退化失效閾值的時間，并分布假設檢驗，結果如圖5所示。三個應力下假設檢驗AD統計量值分別為2.48，2.683，2.4(Weibull分布)，2.357，2.511，2.332(正態分布)。Weibull分布適應性較好，正態分布計算相對簡單。因此應用兩種分布形式的統計分析方法對所得到的退化偽失效時間分析。

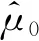
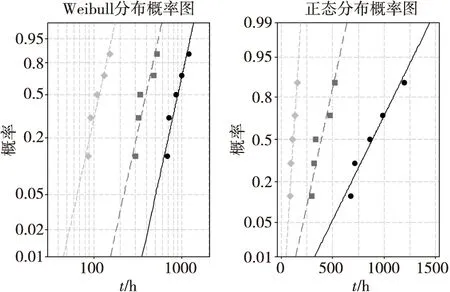
圖5 不同應力下退化偽失效時間的分布假設檢驗Fig.5 Distribution hypothesis test of degenerate pseudo-failure time under different stresses

3.2 基于退化量分布的擬合方法

對不同溫度應力，不同測量時刻的參數退化量分布假設檢驗，結果如圖6所示，不同時刻樣本退化量基本服從正態分布和Weibull分布，且不同時刻所服從的Weibull分布形狀參數m近似相等。

服從正態分布時，均值與均方差隨時間的變化曲線如圖7所示，在不同溫度應力下參數退化量的均值與均方差是時間的線性函數，且求得的方程系數隨應力增加而增加。

假設樣本參數退化量均值與均方差方程系數與溫度的關系滿足Arrhenius加速模型，分布參數與時間、溫度的關系為：

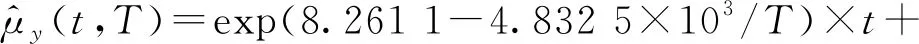
圖6 不同溫度應力，不同測量時刻參數退化量分布假設檢驗圖Fig.6 Hypothesis test chart of parameter degradationdistribution under different temperature stress and measurement time

圖7 不同溫度應力下參數退化量均值與均方差曲線Fig.7 Mean and mean square error of parameter degradation under different temperature stresses

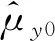
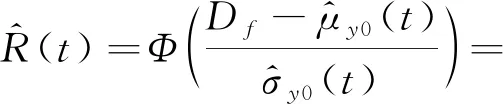
服從Weibull分布時，尺度參數與形狀參數隨時間的變化曲線如圖8所示。尺度參數是時間的線性函數，且方程系數隨應力增加而增加，形狀參數隨應力增加而減少。

假設樣本參數退化量尺度參數方程系數及形狀參數與溫度的關系滿足Arrhenius加速模型，建立相應的加速方程，并求得分布參數與時間、溫度的關系：

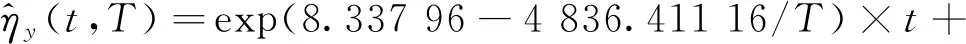
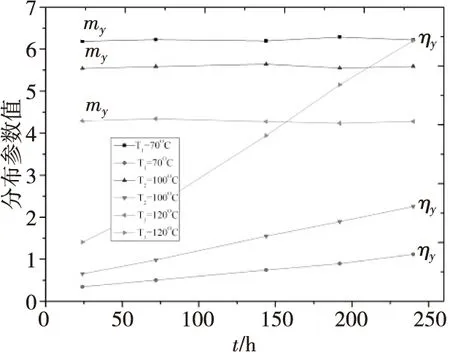
圖8 不同溫度應力下尺度參數與形狀參數曲線(m：形狀參數；η：尺度參數)Fig.8 The parameter of scale and shape under different temperature stress

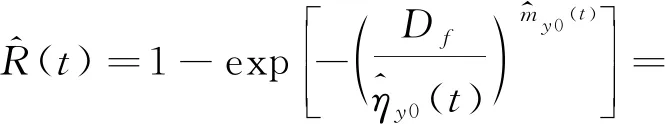
圖9是可靠度評估曲線，基于退化軌跡的擬合方法過程簡潔易懂，兩條曲線形狀接近，服從正態分布的評估結果較保守(曲線偏左)，與假設檢驗結果中正態分布統計量值較小一致。基于退化量分布擬合的方法反映了退化參數所服從分布形式的參數隨時間與溫度應力的變化情況，能夠更準確的反映樣本的實際退化情況。

圖9 不同評估方法得到的MEMS陀螺儀可靠度曲線Fig.9 MEMS gyroscope reliability curve obtained by different evaluation methods

4 結論

本文提出了MEMS陀螺儀加速參數退化的可靠度評估方法。該方法首先對樣本的結構特點和表征性能退化的特征參數、敏感應力及加載方式進行了理論分析，然后形成了基于退化軌跡擬合和退化量分布擬合兩種方式的加速參數退化可靠度評估方法，應用其流程對15個MEMS陀螺儀樣本開展了加速退化試驗，通過對試驗數據分布假設檢驗，選擇恰當的分布形式計算分布參數并驗證退化失效機理的一致性，最后利用建立的加速模型評估樣本在正常使用環境中的可靠度。通過對比實驗結果表明，退化軌跡擬合方法過程簡潔易懂，退化量分布擬合方法建立了分布參數與時間和應力的關系，體現了樣本參數退化之間的差異性，能夠反映MEMS陀螺儀在溫度應力下退化的實際情況，其結果相對退化軌跡的擬合方法準確度更高，因此可促進可靠度指標對樣本實際研制工作的指導。