洪水頻率分析中目標函數的統計試驗研究

康 有，夏傳清，馬順剛

(中國電建集團成都勘測設計研究院有限公司，四川成都610072)

1 研究背景

洪水頻率分析(Flood Frequency Analysis，FFA)是把洪水作為隨機事件，采用頻率分析途徑預測洪水極值事件發生的量級和頻率，以確定水利水電工程在設計標準下工程規模的核心技術[1]。常根據實測洪水、歷史洪水或古洪水等資料估計洪水理論總體分布參數，為水利水電工程提供給定重現期下合理的洪水設計值，其實質是根據設計流域內某水文站的洪水資料進行統計分析，利用實測或調查洪水數據擬合理論總體分布曲線，并作大幅度外延[2-3]。

洪水頻率分析計算過程主要包括樣本抽樣、線型選擇、參數估計、抽樣誤差和區域分析等。參數估計是其最關鍵的技術環節，其計算精度直接影響洪水設計值的可靠性[4]。國內外水文學者對參數估計方法進行了大量研究，并取得了系列重要成果。我國設計洪水計算規范推薦采用適線法(Curve Fit，CF)估計參數值，以P-Ⅲ型分布作為理論總體分布，適線準則(即目標函數)采用離差平方和準則或離差絕對值準則，繪點位置采用頻率期望值公式[5]。研究表明，適線法中目標函數的選擇對確定洪水設計值至關重要，不同的目標函數會得到完全不同的頻率設計值。

由于實測樣本點據在洪水頻率曲線擬合過程中的重要程度不同，水文工作者又提出了加權適線法，采用權重函數確定各個實測洪水樣本點據在目標函數中權重，盡量照顧頻率曲線的中上部點據[6]。影響各樣本點據的權重級別的因素主要包括資料精度、誤差分布、適線目的等。一般假定各樣本點據偏離最優頻率曲線的離散程度服從正態分布，權重函數采用模糊隸屬度函數、高斯函數等[7]。而各種權重函如何選取及其參數取值往往取決于水文工作者的經驗，難以進行定量分析，存在較大的不確定性。

文獻[8]對比分析了基于數值次序統計量的期望值、中值、眾值和頻率次序統計量的期望值等共計4種繪點位置的優化適線法的統計特性，結果表明基于數值次序統計量期望值的洪水頻率分析方法(以下簡稱“NOES”)具有優良的統計特性，并構造一種加權離差絕對值和作為目標函數，其權重函數采用給定頻率P設計值的標準差倒數。NOES方法沒有綜合對比分析基于各種目標函數的洪水頻率分析方法的優劣，其目標函數的選取缺乏一定的依據。

本文采用P-Ⅲ型分布作為洪水理論概率分布，系統闡述了洪水頻率分析中各類目標函數和權重函數，采用統計試驗途徑研究基于各種目標函數和權重函數的NOES方法的優劣，優選出精度高且穩健性優良的目標函數。以雅礱江流域甘孜水文站設計洪水為例，計算不同目標函數和權重函數組合下的洪水設計值，以期為雅礱江流域水利水電工程規劃設計提供更加合理可靠的設計洪水依據。

2 目標函數計算方法

2.1 基本原理

NOES方法假定所研究的洪水隨機變量X服從P-Ⅲ型分布，記作X～Γ(x;a，α，β)，其統計參數為Ex、Cv、Cs。假設洪水隨機變量X的簡單隨機樣本為(X1，X2，…，Xn)，則第m項數值次序統計量X(m)為(x1，x2，…，xn)中從大到小進行排列后(x(1)≥x(2)≥…≥x(n))的第m項。即，X(m)=x(m)；其概率密度函數f(m)(x)、期望值E(X(m)) 、標準差Std(X(m))、信息熵Ent(X(m))計算公式分別為

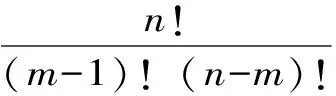
[1-F(x)]m-1f(x)

(1)

(2)

Std(X(m))=E[(X(m))2]-[E(X(m))]2

(3)

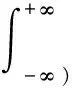
(4)

統計參數為目標函數達到最小值時所對應的優化變量值。洪水頻率分析中目標函數為

(5)

式中，θ為統計參數(即Ex，Cv及Cs)；x(m)為經從大到小排序后第m個洪水樣本(m=1，2，…，n)；E(X(m)，θ)為第m項數值次序統計量X(m)的期望值，即理論頻率曲線上繪點位置的縱坐標值；Wm為權重函數；m為經從大到小排列后的樣本次序；n為洪水樣本序列容量。

2.2 無權目標函數

洪水頻率分析本質上屬于回歸分析，其目標函數(Objective Function)即為統計學中回歸分析的損失函數(Loss Function)，是一種衡量系統在不同參數組合下的損失和錯誤程度的函數。目標函數是用來衡量模型的預測值與真實值的不一致程度，它是一個非負實值函數，其值越小，表示該方法的精度越高。本文結合回歸分析中各類損失函數，構建了以下8種無權目標函數(見表1)：

(1)平均絕對誤差(Mean Absolute Error，MAE)是預測值與真實值之間誤差絕對值的平均值。

(2)平均絕對根誤差(Root Mean Absolute Error，RMAE)是預測值與真實值之間誤差絕對值的平均值的平方根。

(3)平滑平均絕對誤差(Smooth Mean Absolute Error，SMAE)為了增強平方誤差，提高對離群點的魯棒性而提出的；當誤差很小時，SMAE是平方形式的；當誤差很大時，SMAE是絕對值形式的；SAME計算公式中含有一參數δ。當δ→0時，SAME接近MAE，當δ→∞時，SAME接近MSE。

(4)兩權平均絕對誤差(Two Weight Mean Square Error，TWMAE)是分配預測值小于真實值的點據和預測值大于真實值的點據這兩部分點據不同的權重，再計算誤差絕對值的平均值。

(5)四權平均絕對誤差(Four Weight Mean Square Error，FWMAE)是分配預測值小于真實值且頻率小于90%的點據、預測值小于真實值且頻率大于90%的點據、預測值大于真實值且頻率小于90%的點據、預測值大于真實值且頻率大于90%的點據這四部分點據不同的權重，再計算誤差絕對值的平均值。

(6)均方誤差(Mean Square Error，MSE)是預測值與真實值之間誤差平方的平均值。

表1 洪水頻率分析中目標函數計算公式

(7)均方根誤差(Root Mean Square Error，RMSE)預測值與真實值之間誤差平方的平均值的平方根。

(8)對數雙曲余弦誤差(Log Cosh Error，LCE)是預測值與真實值之間誤差的雙曲余弦的對數。

當預測值等于實測值時，損失函數達到其最小值0，取值范圍為0至∞。圖1給出了7種目標函數的變化情況(除FWMAE之外)，其中實測值為100，預測值在-80～120之間。

圖1 各目標函數變化規律示意

2.3 加權目標函數

洪水頻率分析的目的是計算稀遇頻率洪水設計值。在實際工作中，經驗適線法往往照顧頻率曲線上端部分的點據，相當于增加大洪水點據在目標函數中的權重；也就是次序越小，其點據的權重越大[9]。另一方面，大洪水點據的離散程度也會增大，帶來了更多的不確定性；也就是次序越小，其點據的權重越小。本文構建了四類加權目標函數(見表2)。

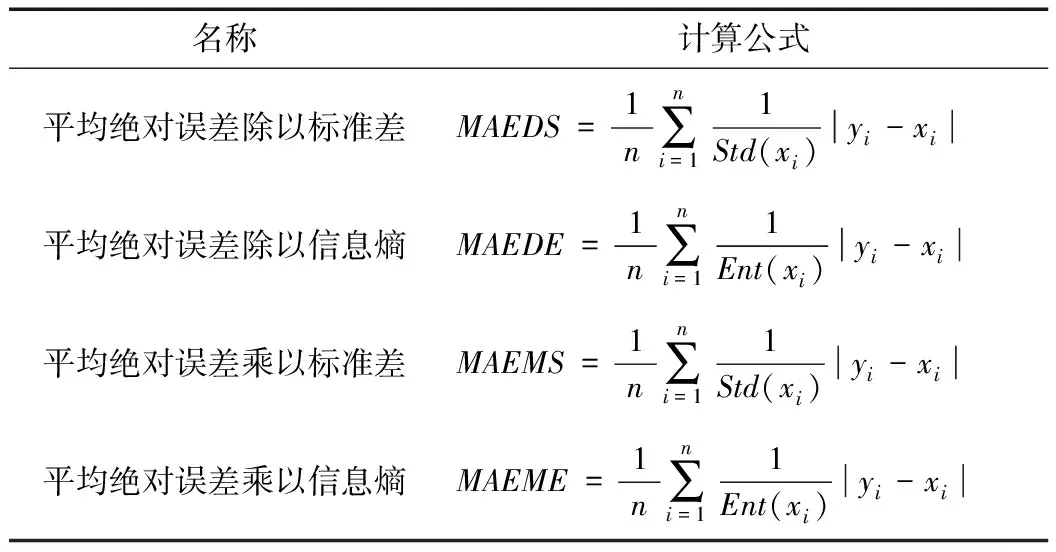
表2 洪水頻率分析中加權目標函數統計

設P-Ⅲ型分布的參數Ex=100、Cv=0.5、Cs=1.5，洪水隨機變量X的簡單隨機樣本為(X1，X2，…，Xn)，計算第m項數值次序統計量X(m)的期望值E(X(m))、標準差Std(X(m))、信息熵Ent(X(m))，并繪制樣本系列的經驗概率密度函數和理論概率密度函數，以及次序統計量X(m)的概率密度函數f(m)(x)，見圖2。

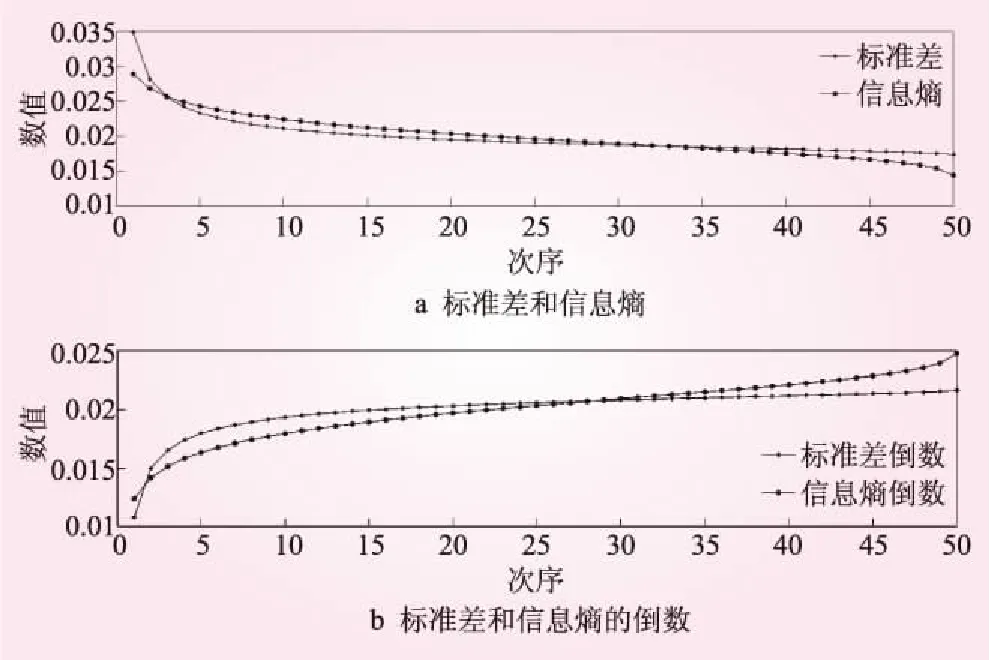
圖2 數值次序統計量標準差和信息熵變化規律示意

由圖2可知，隨著次序m的增大，標準差和信息熵均減小；且在次序m較小時，減小趨勢的梯度更大。圖3給出了在給定總體分布參數的情況下前5個次序統計量的X(m)的概率密度函數，隨著次序m的增大，期望值E(X(m))和實測值x(m)的絕對誤差越來越大。

圖3 數值次序統計量概率密度函數示意

表3 參數估計方法優劣評價指標及其含義

注：Ns表示統計試驗的次數；x表示理論值；yi表示第i次的預測值。

3 目標函數統計試驗

3.1 統計試驗方法

構造一種基于拉丁超立方抽樣、隨機抽樣的統計試驗方法(即Latin Hypercube Sampling & Monte Carlo Statistical Test，簡稱“LM”)，在一定頻率范圍內生成服從指定分布(如P-Ⅲ型分布)的在有限頻率區間內的洪水模擬序列，計算各種統計參數值和頻率設計值，以檢驗不同參數估計方法的優劣[10～11]。LM統計試驗方法計算步驟如下：

(1)將區間[Pmin，Pmax]等間隔分成10×n等份，并假設頻率P在每一個小區間上服從均勻分布，其中Pmin=1/(n×1.5+1)，Pmax=1-Pmin。

(2)在每一個小區間上利用“乘同余法”產生10個服從均勻分布[Pmin，Pmax]的隨機數Mt。

(3)從生成的10×10×n個均勻隨機數Mt中隨機選取n個隨機數ut，并將其順序隨機打亂。

(4)利用“反函數插值法”轉換為指定洪水頻率分布函數F(x)的隨機數xt=F-1(ut)；即根據洪水頻率理論分布的總體參數Cs和均勻隨機數ut(相當于頻率P)計算P-Ⅲ型分布對應的ΦtΦt值。

(5)經算式xt=Ex×(1+Φt×Cv)，即可生成給定統計參數的P-Ⅲ型分布的連序洪水隨機模擬系列(長度為n)，作為實測洪水樣本系列。

(6)參數估計首先采用線性矩法初估參數值，然后采用NOES方法計算其最終值。其中，優化變量選取Ex、Cv與Cs/Cv，適線準則采用相應的目標函數，優化算法采用SCE-UA優化算法。

3.2 優劣評價標準

以參數值和設計值的無偏性及有效性為依據綜合評價各種參數估計方法的優劣[12]。無偏性指標采用標準平均絕對誤差(NMAE)，NMAE為正值表示設計值偏大；反之則偏小；其絕對值越小，則表示該方法的無偏性越好。有效性指標采用標準均方根誤差(NRME)，NRME值越小，則表示該方法的有效性越好，具體見表3。

3.3 統計試驗方案

根據大量流域水文站的實測洪水序列的統計參數規律和統計試驗的實際需求，設定P-Ⅲ型分布統計參數方案編號依次為A、B、C、D、E，總體分布參數的取值分別為Ex=100，Cv=0.3、0.4、0.5，Cs=2.5×Cv、3.0×Cv、3.75×Cv、4×Cv、5×Cv，具體見表4。各組方案的統計試驗次數Ns取500次，樣本容量n取50，設計頻率P取1%，0.5%，0.2%，0.1%。

表4 統計試驗選用的洪水頻率分布統計參數

3.4 無權目標函數試驗結果分析

采用基于MAE、RMAE、SMAE、TWMAE、FWMAE、MSE、RMSE、LCE共8種目標函數的NOES方法，分別計算基于5種統計參數方案共計30種統計試驗方案的統計參數值(包括Ex、Cv與Cs)和洪水設計值XP(P取1%，0.5%，0.2%，0.1%)，以檢驗基于不同目標函數的NOES方法的無偏性和有效性。

(1)參數值統計試驗結果。采用LM統計試驗方法計算基于8種目標函數的NOES方法的參數值統計特性，見圖4。從統計參數值的無偏性來講，RMAE目標函數最優；且偏態系數Cs的NRMSE的絕對值最大，其無偏性最差。從統計參數值的有效性來講，TWMAE目標函數最優；且偏態系數Cs的NRMSE的絕對值最大，其有效性最差。

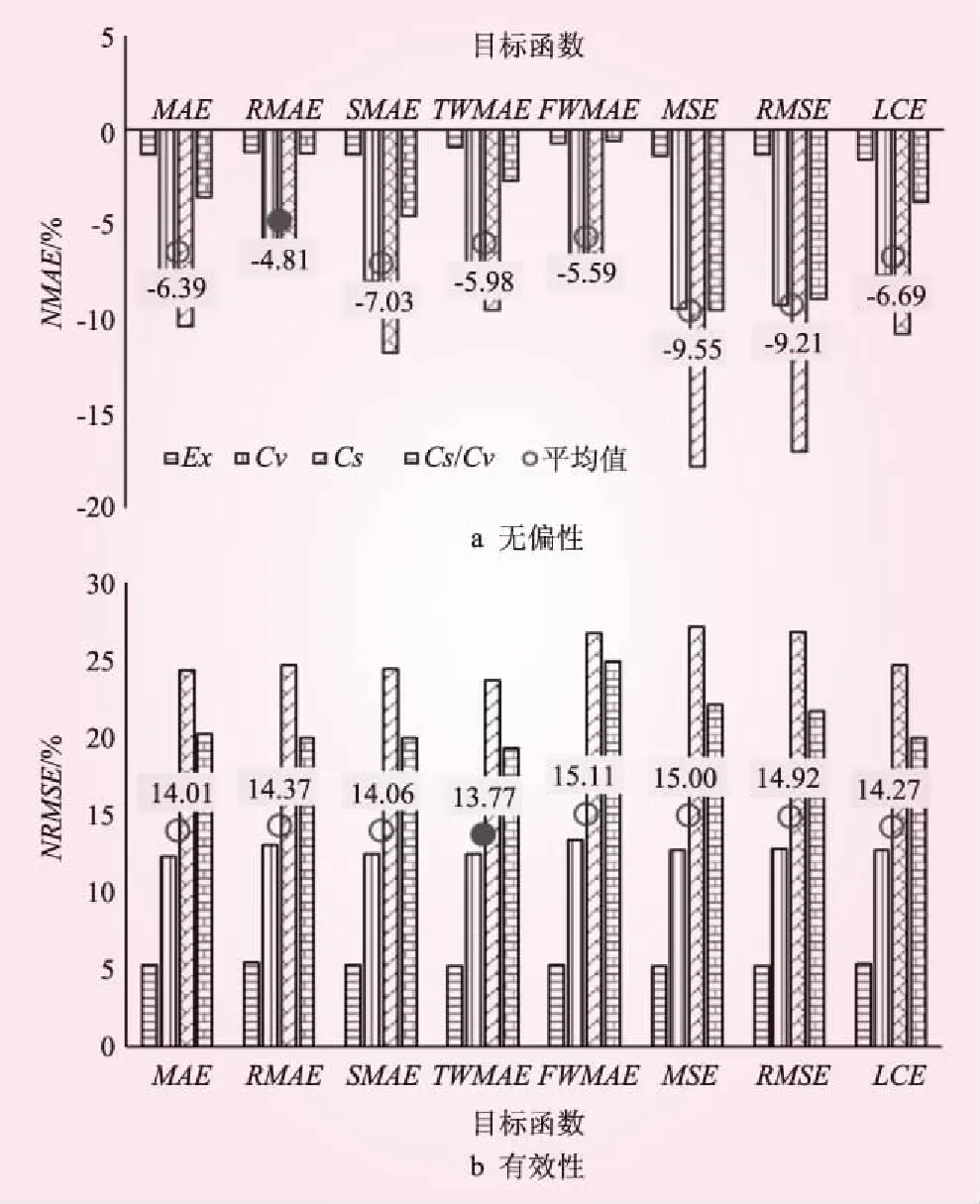
圖4 NOES方法的統計參數值無偏性和有效性

(2)設計值統計試驗結果。采用LM統計試驗方法計算基于8種目標函數的NOES方法的設計值統計特性，見圖5。

圖5 NOES方法的頻率設計值無偏性和有效性

從頻率設計值的無偏性來講，RMAE目標函數最優；且隨著頻率P的減小，NMAE的絕對值增大，頻率設計值的無偏性逐漸變差。從頻率設計值的有效性來講，TWMAE目標函數最優；且隨著頻率P的減小，NRMSE的絕對值增大，頻率設計值的有效性逐漸變差。

3.5 加權目標函數試驗結果分析

采用基于MAE、MAEDS、MAEDE、MAEMS、MAEME共5種目標函數的NOES方法，分別計算基于5種統計參數方案共計30種統計試驗方案的統計參數值(包括Ex、Cv與Cs)和洪水設計值XP(P取1%，0.5%，0.2%，0.1%)，以檢驗基于不同加權目標函數的NOES方法的無偏性和有效性。

(1)參數值統計試驗結果。采用LM統計試驗方法計算基于4種加權目標函數的NOES方法的參數值統計特性，見圖6。從統計參數值的無偏性來講，MAEDS目標函數最優；且偏態系數Cs的NMAE的絕對值最大，其無偏性最差。從統計參數值的有效性來講，MAEDE目標函數最優；且偏態系數Cs的NRMSE的絕對值最大，其有效性最差。

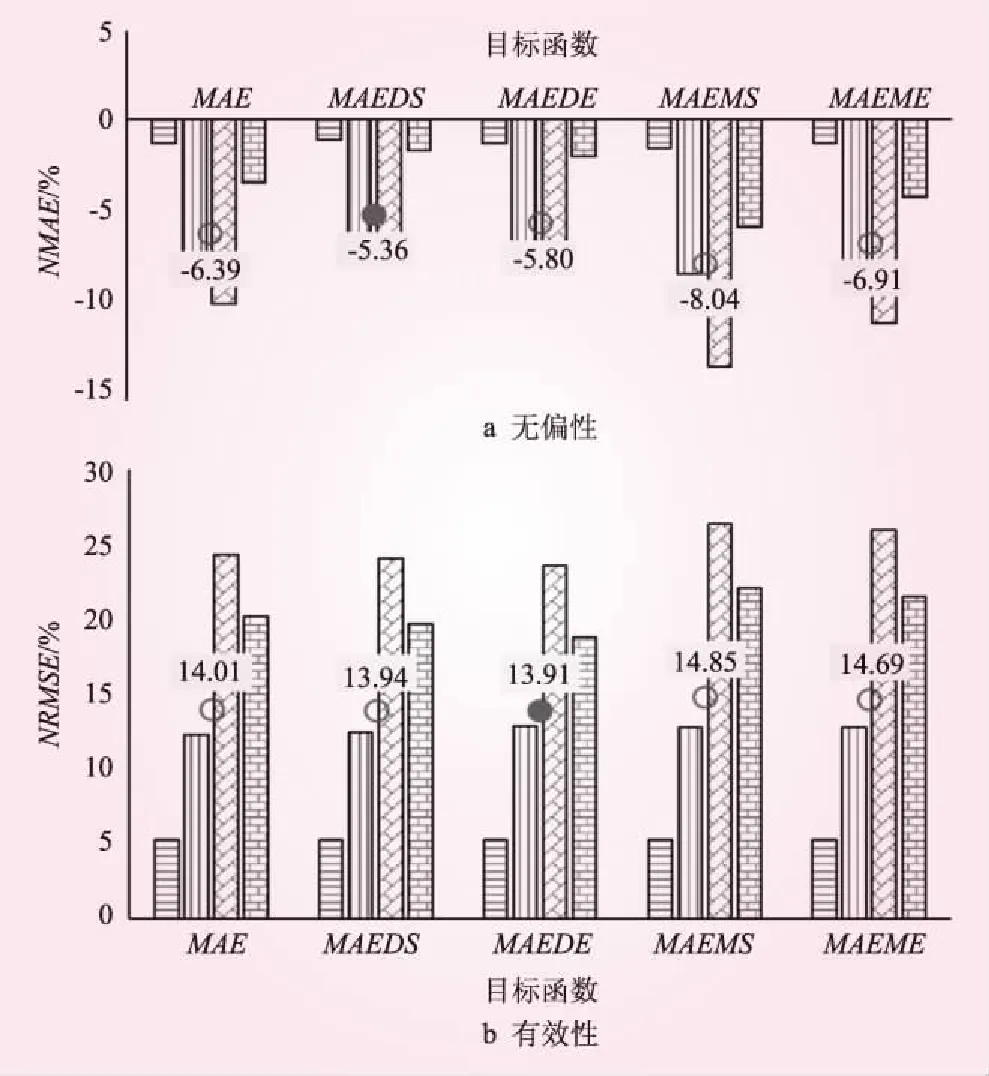
圖6 基于不同加權目標函數的NOES方法的統計參數值無偏性和有效性

(2)設計值統計試驗結果。采用LM統計試驗方法計算基于5種加權目標函數的NOES方法的設計值統計特性，見圖7。從頻率設計值的無偏性來講，MAEDS目標函數最優；且隨著頻率P的減小，NMAE的絕對值增大，頻率設計值的無偏性逐漸變差。從頻率設計值的有效性來講，MAEDS目標函數最優；且隨著頻率P的減小，NRMSE的絕對值增大，頻率設計值的有效性逐漸變差。

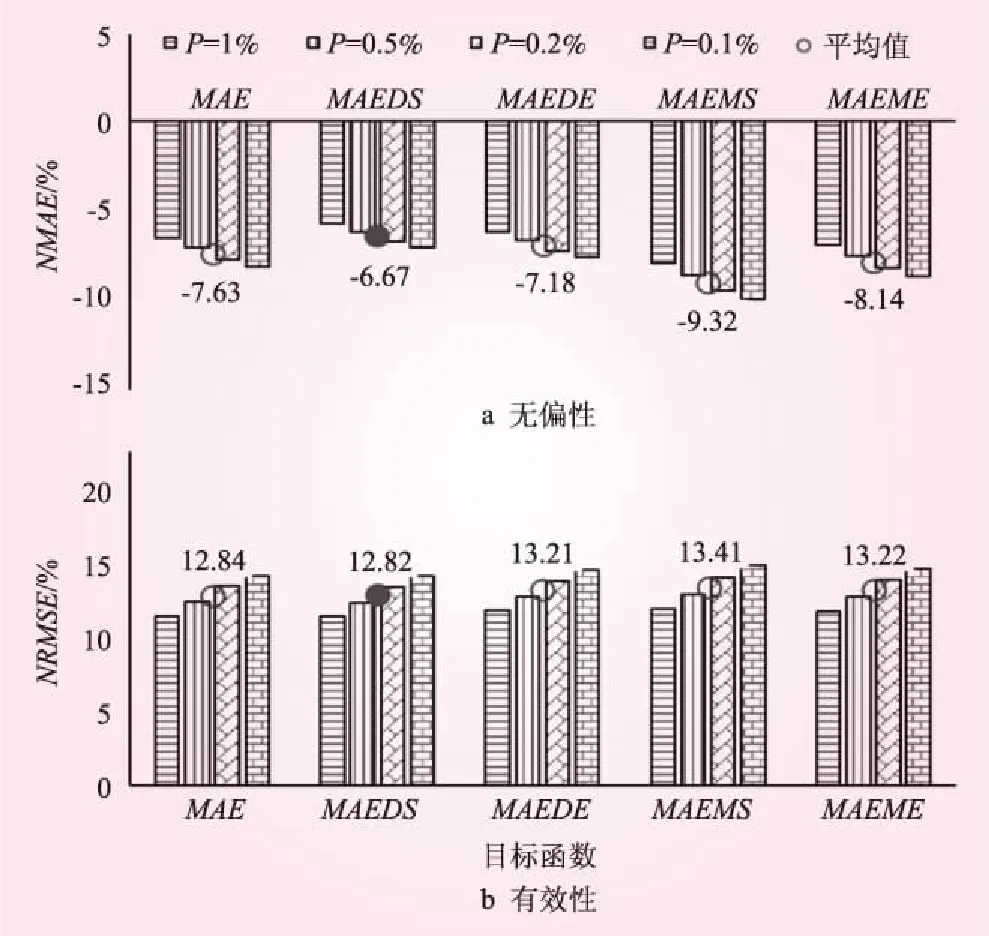
圖7 基于不同加權目標函數的NOES方法的頻率設計值無偏性和有效性

3.6 對比分析

從圖4、5可知，從統計參數值和頻率設計值的無偏性和有效性來講，采用平均絕對根誤差RMAE作為洪水頻率分析的目標函數，可以有效減少洪水設計值的無偏性。從圖6、7可知，從統計參數值和頻率設計值的無偏性和有效性來講，采用平均絕對誤差除以標準差MAEDS作為洪水頻率分析的目標函數，可以有效提高洪水設計值的有效性。在洪水頻率分析目標函數的合理選取中，目標函數的選擇取決于許多因素，包括是否有離群點、參數估計方法、誤差分布規律等，沒有一個通用的目標函數可以適用于所有統計參數的求解。綜合分析，從統計參數值、頻率設計值的無偏性和有效性整體上來講，采用平均絕對根誤RMAE為目標函數的NOES方法整體上精度高且穩健性優良，尤其在設計值無偏性上的優勢更為明顯。

4 實例分析

4.1 基本資料

雅礱江流域位于青藏高原東部，為金沙江第一大支流，干流河道全長1 535 km，流域面積12.8萬km2。雅礱江流域甘孜水文站控制流面積為3.3萬km2，自1952年4月設站至今。經插補延長后，采用年最大值抽樣法(Annual Maximum Sampling，AMS)獲得甘孜站1952年～2015年共計64 a的洪水年最大值系列(見圖8)。

4.2 設計洪水

根據甘孜站1952年～2015年共計64 a的洪水年最大值系列，以P-Ⅲ型分布作為理論總體分布，首先采用線性矩法計算統計參數初始值；然后采用NOES方法分析計算統計參數值，優化變量選取Ex、Cv與Cs/Cv，適線準則采用MAE和RMAE目標函數，優化算法采用SCE-UA算法；計算給定頻率P(1%、0.5%、0.2%和0.1%)的設計洪水XP，具體見圖9、10。

圖8 雅礱江流域甘孜站洪水樣本系列示意

圖9 甘孜站洪水頻率曲線優化適線成果

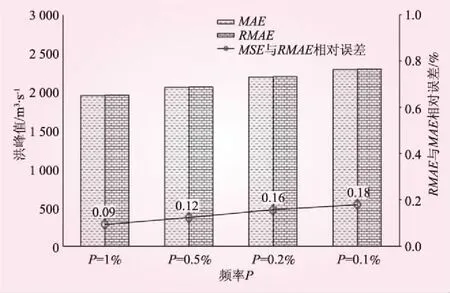
圖10 甘孜站基于不同目標函數的設計洪水對比示意

由圖10可知，采用RMAE為目標函數的NOES方法計算的洪水設計值要比采用MAE為目標函數的NOES方法計算的洪水設計值偏大0.09%～0.18%，其平均值為0.14%；隨著頻率P的減小，兩者的絕對誤差逐漸增大。

5 結 論

結合洪水頻率分析適線法的計算目的和洪水樣本誤差規律，構建了一種新的目標函數——平均絕對根誤差RMAE，為采用NOES方法計算洪水設計值時合理選取目標函數提供了試驗依據，其研究結論如下：

(1)從統計參數值、頻率設計值的無偏性和有效性整體上來講，采用平均絕對根誤差RMAE為目標函數的NOES方法整體上精度高且穩健性優良，尤其在設計值無偏性上的優勢更為明顯。

(2)由于實測洪水樣本序列的隨機性和復雜性，各個樣本點據在目標函數中的作用尚無統一的規律；基于傳統水利水電工程水文設計經驗，一般設計中考慮大洪水點距具有更大的權重，構建一種隨著次序增大權重減小的權函數；或者基于誤差規律，考慮大洪水點距具有更大的方差或信息熵，構建一種隨著次序增大權重增大的權函數；經統計試驗表明，兩者均不能有效提高洪水設計值的統計特性，反而會增大洪水設計值的不確定性。