基于模糊預測的INS/視覺無人機自主著陸導航算法*

洪 亮,章 政,2,3*,李亞貴,李宇峰,張艦棟

(1.武漢科技大學信息科學與工程學院,武漢 430081;2.武漢科技大學機器人與智能系統研究院,武漢 430081;3.武漢科技大學冶金自動化與檢測技術教育部工程研究中心,武漢 430081)

自主著陸是無人機自主飛行系統中的重要環節,通過機載導航設備獲取實時、精確的位姿信息是實現無人機安全、有效著陸的前提和基礎[1]。相比于GPS導航方式[2],基于視覺的無人機著陸導航方式可全覆蓋、獨立獲取著陸點周圍高精度的三維空間反饋信息,對環境要求較低,具有抗干擾能力強、精度高和功耗低等特點[3]。目前,慣性導航系統INS(Inertial Navigation System)與視覺傳感器構成INS/視覺組合導航系統已成為無人機自主著陸導航系統設計的主要趨勢[4-5]。

對于基于INS/視覺的無人機自主著陸導航系統,常采用卡爾曼濾波KF(Kalman Filter)實現INS與視覺傳感器的數據融合。文獻[6]由視覺位姿估計系統得出飛行器的位姿信息,通過卡爾曼濾波實現位置、姿態匹配;文獻[7]構建了一種非線性濾波器實現了慣導誤差估計,在提高算法效率的同時有效地避免了無跡卡爾曼濾波中由于矩陣開方運算導致的濾波失效問題;文獻[8]提出了一種基于圖像輔助慣導的擴展卡爾曼濾波方法,使得基于視覺輔助慣導的組合導航系統逐漸成為一種新的導航模式;文獻[9]通過多估計中心的加權并將擴展卡爾曼濾波與單目視覺位姿估計相結合,提高了無人機的位姿估計精度。上述研究主要是利用視覺傳感器的觀測數據修正INS的估計誤差,再結合卡爾曼濾波實現無人機的位姿估計,由此避免INS定位誤差隨時間累積的缺陷。

然而,在無人機實際著陸過程中,機載攝像頭獲取著陸點附近圖像信息是一個動態測量過程,其視覺觀測數據會隨著時間和空間而變化且包含了飛行環境中的各種干擾信息。因此,通過透視投影模型解算出的視覺觀測數據存在觀測噪聲與解算誤差[10],直接融合INS和視覺的數據易導致系統額外誤差[11]、位姿狀態估計不收斂[12-13]等問題。此外,由于受到機載傳感器低主頻、無硬件浮點運算等限制,視覺觀測數據的更新周期長,從而影響無人機位姿估計的實時性。

基于上述分析,考慮到模糊邏輯[14]可有效處理機載攝像頭獲取觀測數據的時變性和不確定性,本文設計了一種基于模糊預測的INS/視覺無人機自主著陸導航算法。首先,采用模糊數描述機載攝像頭解算所得的觀測數據,在INS數據更新的同時,構造基于歷史觀測數據的模糊預測模型,由此預測機載攝像頭當前時刻的觀測數據;然后,設計基于狀態量同步更新的卡爾曼濾波器,對INS產生的誤差進行修正,得到無人機的位姿估計,從而避免直接融合INS與視覺數據導致系統額外誤差的問題,提高了無人機的位姿估計精度;最后,通過基于四旋翼無人機平臺的實測實驗驗證了本文算法的有效性和實時性。

1 基于INS/視覺的無人機自主著陸導航系統設計

1.1 自主著陸導航系統的坐標系定義

本文所設計的INS/視覺無人機自主著陸導航系統主要包括:四旋翼無人機、機載攝像頭和著陸地標,其位姿關系如圖1所示。

圖1 坐標系對應關系

Oc-XcYcZc為四旋翼無人機和機載攝像頭的坐標系,坐標系原點Oc為無人機的機體重心。X軸和Y軸位于無人機機體平面內,Y軸指向無人機前進方向,X軸指向無人機左側方向,Z軸指向無人機上升方向。

Op-XpYp為圖像坐標系,平行于無人機機體平面,Y軸指向無人機前進方向,X軸指向無人機左側方向。

Ow-XwYwZw為著陸地標坐標系,坐標系原點Ow為著陸地標的幾何中心。X軸和Y軸位于著陸地標平面內,Y軸指向地理正北方向,X軸指向地理正西方向,Z軸垂直于著陸地標平面向上。

1.2 基于INS/視覺的無人機自主著陸導航算法

針對INS/視覺的無人機自主著陸系統的特點,將模糊預測用于導航算法中,算法結構圖如圖2所示。

圖2 基于INS/視覺的無人機自主著陸導航算法

首先,對圖像中的著陸地標進行特征點提取,通過視覺解算得到無人機在地標坐標系下的位置觀測數據。針對視覺觀測數據存在不確定性問題,采用三角模糊處理視覺解算得到的觀測數據。然后,針對無人機非線性、強耦合和靜態不穩定的特性,考慮到機載計算機的處理能力有限,在慣導數據更新的同時,利用模糊預測的方法預測視覺傳感器的位置觀測數據。最后,在得到視覺觀測數據的一步預測值后,通過卡爾曼濾波器修正慣導的加速度零偏、速度誤差和位置累計誤差,得到用于無人機位置反饋控制的最優估計值,達到無人機自主著陸中對位姿估計實時性的要求。

2 基于模糊預測的INS/視覺無人機位姿估計算法

2.1 視覺觀測數據解算

對機載攝像頭拍攝的圖像進行Harris特征點檢測,提取著陸地標的特征點。根據透視投影模型和剛體旋轉平移的坐標變換原理,結合圖1所示的坐標系對應關系,著陸坐標系中的特征點(xw,yw,zw)與其對應圖像坐標中像素點(u,v)的關系如下:

(1)

式(1)中zc為特征點(xw,yw,zw)在相機坐標系的坐標,K為相機參數,R,T為無人機相對于地標的旋轉矩陣和偏移矩陣,分別為:

R=

(2)

(3)

式(2)中,θ,φ,ψ分別為俯仰角、橫滾角和偏航角,式(3)中,Tz為無人機相對于地標的高度,Tx和Ty為無人機相對地標的水平偏移量。

由于zc和攝像頭參數K為已知量,因此根據若干組地標中特征點(xw,yw,zw)在圖像中的像素(u,v),就可以求得旋轉矩陣R和偏移矩陣T,獲取無人機相對于地標的姿態和位置信息。

圖3 觀測量預測及狀態同步更新

2.2 基于模糊預測的視覺觀測數據分析及處理

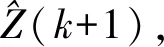
以X軸位置的觀測數據為例,考慮到二次函數可以表征大部分目標的運動軌跡,在短時間內攝像頭的位置觀測數據Tx(t)采用式(4)所示的模糊序列模型描述:

Tx(t)=r0+r1t+r2t2+ε

(4)

(5)

(6)

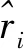
取k+1時刻以前的L個時刻的攝像頭歷史位置觀測數據Tx1,Tx2,…,TxL,令mt=max{Txt-1,Txt,Txt+1},nt=min{Txt-1,Txt,Txt+1}(t=2,3,…,L-1),m1=max{Tx1,Tx2},n1=min{Tx1,Tx2},mL=max{TxL-1,TxL},nL=max{TxL-1,TxL}。將這L個數據進行模糊處理,構成如式(7)所示的一組三角模糊數st(x)。

(7)

(8)

(9)

式(9)中,權重ω={ω0,ω1,ω2}由普通線性回歸給出:

(10)

(11)

2.3 基于卡爾曼濾波器的狀態量同步更新

以Ow-XwYwZw著陸地標坐標系為導航坐標系,在INS更新時,利用攝像頭觀測數據對無人機INS估計出的位置狀態進行誤差修正。

無人機在降落階段需要獲取OwXw、OwYw、OwZw方向上的3個位置與3個速度狀態量,選取無人機的狀態量為:

(12)

(13)

由勻加速直線運動方程,得到系統狀態方程在k時刻離散化為:

X(k)=AX(k-1)+BU(k)+Γω

(14)

式(14)中系統狀態轉移矩陣A、驅動矩陣B、過程噪聲分布矩陣為Γ為:

(15)

(16)

(17)

其中DT為攝像頭觀測數據的更新周期。

Zk=HXk+Vkν

(18)

式中的系統狀態量為全觀測,故狀態觀測矩陣H=I6×6。

系統過程噪聲協方差矩陣Qk與靜態觀測噪聲矩陣Rk需要根據實際使用來整定:

(19)

(20)

先驗協方差矩陣與卡爾曼濾波增益更新的更新表達式為:

P(k+1|k)=AP(k|k)AT+ΓQΓT

(21)

K(k+1)=P(k+1|k)HT[HP(k+1|k)HT+R]-1

(22)

(23)

(24)

式(24)中,ΔT為當前INS的更新時刻k+1與最近一次觀測傳感器的更新時刻ko的時間間隔。ΔT和ko均來自計算機系統的測量時間。

后驗協方差矩陣更新如下:

P(k+1|k+1)=[I6×6-K(k+1)H]P(k+1|k)

(25)

根據上述分析,本文設計的基于模糊預測的INS/視覺無人機位姿估計算法框圖如圖4所示。

在無人機INS/視覺組合導航降落系統中,針對攝像頭觀測傳感器數據滯后特性引起的狀態估計誤差甚至發散問題,本文利用模糊預測的方法,同步預測滯后的觀測傳感器數據。考慮到低成本微處理器的實際處理能力有限,利用卡爾曼濾波對INS的累計誤差進行修正,減小了計算量,保證了融合算法的實時性。

3 組合導航系統設計與實驗

本文自主設計了無人機自主著陸導航實驗平臺并設計了三組實驗,驗證了本文算法的實時性、有效性和實用性。

3.1 實驗配置介紹

無人機自主著陸導航實驗平臺包括四旋翼無人機和著陸地標,如圖5所示。四旋翼無人機由飛行控制器、電子調速器、無刷電機、螺旋槳、機架、電池、低壓報警器、遙控器和視覺模塊等部分組成。四旋翼無人機的總重量0.865 kg,機體對角線軸距為33 cm,高12 cm。

四旋翼無人機的系統硬件結構如圖6所示,飛行控制器采用32位微處理器STM32F103RCT6,主頻為72 MHz。姿態傳感器采用六軸陀螺儀加速度計傳感器MPU6050,磁力計采用IST8310,氣壓計為SPL06-001。視覺模塊由OV5647攝像頭模組和“樹莓派”微型計算機組成。微型計算機的CPU采用Broadcom BCM2837,內存1G,安裝了Raspbian操作系統和OpenCV 3.4.1視覺開發庫。

圖6 飛控系統結構示意圖

本文在每幀圖像中選取8個特征點,求解無人機的偏移矩陣T,然后通過串口實時發送給飛行控制器。飛行控制器中INS更新頻率為200 Hz,根據實際調試,選取過程噪聲矩陣Qk與觀測噪聲矩陣Rk中參數a、b、c、d分別為2.0×10-6、0.015、0.075、2.5,貼近度h0取0.7。

3.2 實驗及結果分析

①實時性對比實驗

在實時性對比實驗中,以高度方向位置融合為例,大約1 s左右將無人機快速拉至降落引導地標正上方約90 cm高度位置,得到同一實驗條件下本文組合導航算法和常規卡爾曼算法的實驗數據如圖7所示,算法的收斂時間和均方根誤差如表1所示。

表1 實時性對比實驗的數據分析

從圖7(a)和表1的實驗數據可以看出,本文設計的無人機組合導航算法得到的高度位置估計值相比于常規卡爾曼濾波算法,能一次性快速地跟蹤視覺傳感器解算出的高度變化過程,并且迅速收斂。結合圖7(b)的實驗數據,在動態過程中,由于觀測傳感器更新周期長,短時間內原始觀測高度更新不及時,而經模糊預測得到的觀測數據能夠較為準確地描述觀測數據的變化。使得圖7(a)中組合導航得到的高度估計值相位超前于視覺傳感器觀測的高度,提高了位置估計的實時性。

圖7 實時性對比實驗

②無人機實際飛行實驗

在無人機實際飛行實驗中,無人機初始狀態為定點懸停狀態,位于(10,-10,40),3 s后利用遙控器依次飛行至(10,10,40)、(-10,10,40)、(0,0,40)。懸停3 s后,控制遙控器油門動作位,讓無人機在高度方向做快速機動動作,最后,懸停在(0,0,22)處。無人機實際飛行實驗結果如圖8所示,X、Y、Z三方向的均方根誤差和誤差最大值如表2所示。

圖8 實際飛行融合實驗數據

方向誤差最大值/cm常規算法本文算法均方根誤差常規算法本文算法XYZ4.75.96.24.65.34.10.160.190.150.110.130.09

表2的數據表明本文組合導航算法相比于常規算法融合得到的位置估計精度更高,由圖8的位置融合實驗結果可知,靜態時慣導估計狀態和攝像頭的觀測狀態基本吻合,經過融合得到的估計狀態數據會更加平滑,受觀測傳感器自身噪聲影響,融合得到的估計狀態數據會有一定的波動,其波動范圍遠小于觀測狀態數據自身的波動。觀察由靜止到運動的過程,攝像頭得到的觀測狀態存在一定的滯后現象,動態過程中融合得到的估計狀態相位始終超前于攝像頭的觀測狀態。觀察動態到靜止的運動過程可知,融合得到的位置估計會迅速收斂到位置觀測量。本文設計的組合導航算法提高了位姿估計的實時性,同時位姿估計數據能保證長時間收斂。

③自主著陸實驗

在自主降落實驗中,降落地標安裝在移動平臺上,利用遙控器控制無人機飛行在平臺上方1.5 m后,將自主降落對應通道打到高位,無人機自動完成著陸控制。經過多次實驗,著陸后無人機與地標中心的平均偏移誤差如表3所示。

表3 不同速度下降落誤差對比

表3的實驗數據表明了本文INS/視覺組合導航算法相比于常規算法能夠為無人機的自主降落控制提供更為實時、準確的反饋數據,滿足四旋翼無人機的自主著陸要求。

4 結束語

在INS/視覺導航無人機自主著陸導航系統中,由于視覺觀測數據存在不確定性噪聲、更新慢等問題,導致組合導航算法的精度和實時性受到限制。鑒于此,本文設計了一種基于模糊預測的INS/視覺無人機自主著陸導航算法。考慮到機載處理器的硬件限制,本文從卡爾曼濾波模型出發,采用三角模糊數處理視覺觀測數據,減小了觀測噪聲和解算誤差帶來的濾波估計誤差。在INS數據更新時,利用模糊預測的方法同步預測滯后的視覺觀測傳感器數據,相比于常規卡爾曼濾波算法,提高了無人機位姿估計的實時性。實測實驗結果表明利用本文設計的組合導航算法能實時、準確地估計無人機相對于地標的位姿信息,滿足無人機自主著陸所需數據的實時性與動態跟蹤精度要求,為基于INS/視覺的無人機自主著陸系統提供了一種簡單可靠的組合導航算法。