基于GA-BP神經網絡溫漂補償的十字正交型熱溫差式測風儀*

劉 洋,行鴻彥*,侯天浩

(1.南京信息工程大學,氣象災害預報預警與評估協同創新中心,南京 210044;2.南京信息工程大學,江蘇省氣象探測與信息處理重點實驗室,南京 210044)

風速風向的測量對我們的生活有著重大意義,在航空領域、農業領域、工業領域、環境監測領域等都發揮著重要作用。目前常用的測量方法有機械測量法、超聲波測量法以及熱式測量法等。機械測量法因存在旋轉結構,易受惡劣環境的影響,旋轉軸因磨損需定期維護[1],超聲波測量法雖對環境影響的敏感度較低且沒有機械磨損結構,但如何消除其測風時的陰影效應是現在超聲波測風領域的一大難點[2]。熱式測量法利用熱力學原理,設計出來的風速儀因成本低、體積小、精度高而被逐漸廣泛應用于各個領域。

早在1902年Shakepear在伯明翰就開始了熱線風速儀的原理性實驗,1929年,Drydew和Planiol發展了熱滯后的電子補償原理,將熱式風速測量推動到脈動速度和湍流度的測量。到了20世紀60年代,國外已對熱式風速測量法有了較為成熟的研究。與國外相比,我國對熱式風速測量法的研究起步較晚,因此很多熱式風速儀都是從國外購入,其價格高、質量低[3]。為了不依賴進口,國內越來越多的研究者開始投入這方面的研究,但目前市場上銷售的熱式風速儀普遍還不能測量風向,因此,設計出一款體積小、成本低、精度高、既能測量風速又能測量風向的熱式風速儀具有重要意義[4]。

本文結合FLUENT流體仿真提出了一種十字正交型熱溫差式測風儀的設計方法,根據十字型導管內上下游溫度差求得風速,且該設計可通過正交分解得到二維空間內任意方向的風速以及風向角。為降低環境溫度對測量精度的影響,本文提出遺傳算法優化BP神經網絡算法補償溫漂誤差,實驗結果表明,該補償算法對測風儀的溫度漂移有較好的抑制效果。

1 基于GA-BP熱溫差型測風儀的測風原理

1.1 熱溫差式測風原理

熱式測風儀是在熱場和風場直接作用下進行工作的,其工作原理是一個涉及熱學、流體力學等多種學科的綜合性理論。因此,熱式測風儀的結構中需包括加熱元件——提供高于環境溫度的熱場,和測溫元件——檢測氣體流動所導致的熱場溫度變化,通過加熱元件提供熱量,測溫元件測量風吹過時帶來的熱量差來獲取風速的信息。熱式測風儀檢測原理又可主要分為熱損失型、熱脈沖型和熱溫差型三種類型,熱損失型和熱脈沖型因不能測量風向,本文不予考慮,僅重點介紹熱溫差型測風原理。

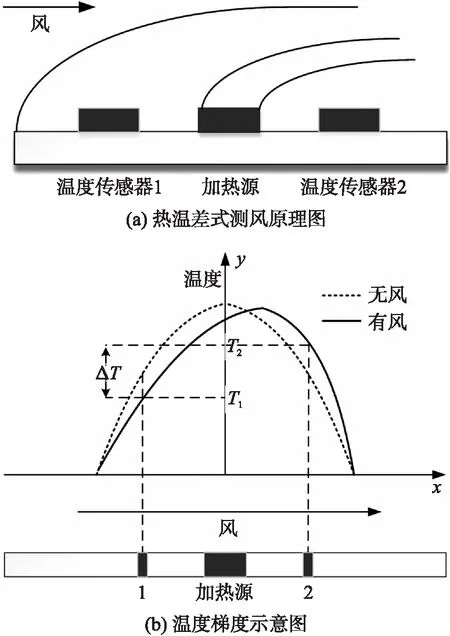
圖1 測風原理圖及溫度場分布圖

熱溫差式測風原理圖如圖1(a)所示。測風儀中間為一恒溫加熱源,兩溫度傳感器在該加熱源兩側成對稱分布。溫度梯度示意圖如圖1(b)所示,無風吹過時,溫度場對稱分布,兩溫度傳感器值恒定不變;有風吹過時,流體帶走加熱棒的熱量,正對風的上游熱源損失熱量必定大于下游損失熱量,溫度場偏離對稱分布,上下游測溫點則會產生溫差ΔT=T2-T1,此溫差是風速大小的函數,當風速較小時測風儀會有較大的靈敏度,即產生的溫差較大;而隨風速的增加,靈敏度會逐漸降低,直到風速很大時達到飽和值。因此只要通過檢測上下游溫度傳感器差值便可得相應風速[5-6]。

1.2 正交式熱溫差測風原理

為在測量風速的同時測出風向,本文基于正交分解法設計了十字型熱溫差式測風儀,將溫度傳感器與恒溫熱源分別置于兩交疊的圓管(導風管)中。其結構俯視圖如圖2所示。

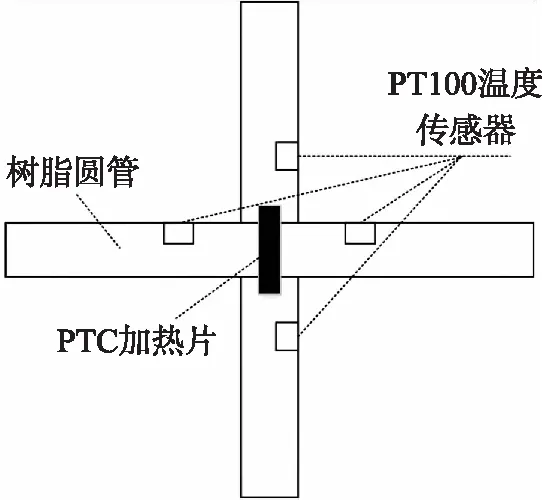
圖2 測風儀俯視圖

十字型熱溫差式測風儀在任意時刻,都會有一個或者兩個導風管的管口處于來流中,只要建立好合適的坐標系(坐標系的軸沿著導風管入口方向),便可對風速進行正交合成與分解。因此,通過測量每一個導風管的風速分量即可反演出實時風速從而還原出實時風向。以平面直角坐標系為例,當十字型熱溫差式測風儀所處平面與風速V平行時,其位置關系如圖3 所示(AB與Y軸重合,CD與X軸重合)。

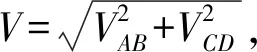
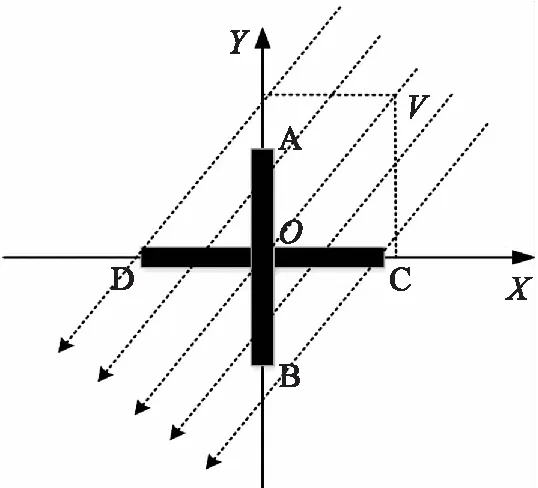
圖3 風速風向測量原理示意圖

設風速與X軸成θ角,則:

(1)

(2)

即:

(3)

1.3 基于GA-BP的測風優化算法

在實際測風中,環境溫度的變化會對風速測量精度造成影響,因此本文提出了一種利用遺傳算法(GA)優化BP神經網絡算法來補償溫度漂移的測風優化算法。

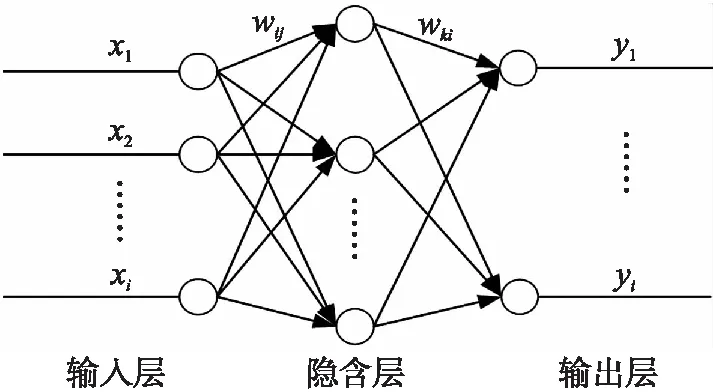
圖4 BP神經網絡結構圖

BP神經網絡結構圖如圖4所示,它是一種多層前饋網絡,其特點為信號前向傳播,誤差反向傳播,由輸入層、隱含層、輸出層三部分組成,且每一層的神經元狀態只影響下一層的神經元狀態。樣本由輸入層輸入,經隱含層處理后發送至輸出層,若輸出層得到的值與目標值存在誤差,則執行誤差反向傳播操作,根據誤差不斷調整網絡權值和閾值,從而達到最佳效果[7-9]。

遺傳算法(Genetic Algorithm)是一種引入生物界自然選擇和自然遺傳機制的全局尋優搜索算法。某一初始種群中的個體通過遺傳算法中的選擇、交叉和變異篩選后,適應性好的個體被保留,反之被淘汰,這樣新一代群體永遠優于上一代,反復循環,直至尋得全局最優。

由于BP神經網絡存在易陷入局部極小值和收斂速度慢的缺點,因此將GA與BP神經網絡相結合。先利用GA優化BP神經網絡所需要的權值和閾值,再利用BP神經網絡求解,以達到全局尋優和提高收斂速度的目的[10-11]。

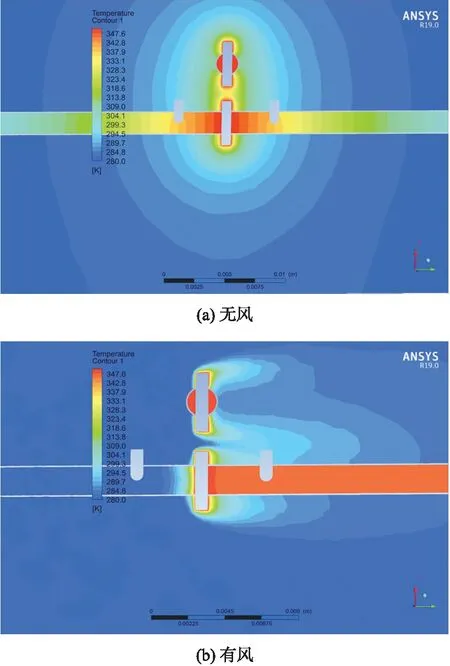
圖5 溫度場分布圖

2 流場仿真分析

為驗證溫差測風理論的可行性,在實際測量前搭建模型進行仿真實驗:首先用SpaceClaim建立十字型熱溫差式測風儀的模型,其次用ANSYS Meshing軟件規劃四面體網格,最后再導入FLUENT軟件,選用k-e模型并開啟能量交換選項,開始測風流體仿真。其仿真的溫度場分布云圖如圖5所示:在無風狀態下,導風管內的溫度場以熱源為中心呈對稱分布,即上下游溫度傳感器周圍的溫度相同;在有風狀態下,風流入導風管內,風因熱交換效應將導風管內上游經加熱片加熱的熱空氣帶至下游,在此期間,風依舊被不斷加熱,當風流經下游時,下游溫度將明顯高于上游,溫度場偏離對稱分布,因此上下游傳感器所測得數值存在溫差。

設定環境溫度分別為-10 ℃、0 ℃、10 ℃、20 ℃、30 ℃、40 ℃,風速分別為1 m/s、2 m/s、3 m/s、4 m/s、5 m/s、6 m/s、7 m/s、8 m/s,進行不同環境溫度、不同風速下的流體仿真。仿真得的溫度差值擬合曲線如圖6所示。由圖6可知,隨著環境溫度的升高,因風速來流而產生上下游溫差呈現略微下降趨勢,風速和溫差有強相關性,不同風速所對應的溫差不同。實驗結果與1.1節理論整體相符,故熱溫差法測風可行。

圖6 仿真數據擬合曲線圖

3 實測數據采集與分析

3.1 熱溫差測風儀測量電路設計

熱溫差式測風儀硬件系統框圖如圖7所示,由STM32F103RCT6單片機、AD7794模數轉換模塊、PT100鉑電阻式溫度傳感器以及PTC恒溫加熱片組成十字正交型熱溫差式測風儀。其采集數據由RS232串口發送至上位機。

圖7 硬件系統框圖

3.2 實驗平臺搭建

利用十字正交型熱溫差式測風儀搭建如圖8所示的實驗平臺。該平臺由測風儀、高低溫實驗箱、可調速鼓風機、上位機等組成。高低溫試驗箱的可調溫度范圍為-60 ℃至120 ℃,用于模擬環境溫度;可調速鼓風機用于改變來流大小;正交十字型熱溫差式測風儀用支架支撐并插入塑料泡沫中。

圖8 實驗裝置圖

3.3 數據擬合分析

在環境溫度分別為-10 ℃、0 ℃、10 ℃、20 ℃、30 ℃、40 ℃,風速分別為1 m/s、2 m/s、3 m/s、4 m/s、5 m/s、6 m/s、7 m/s、8 m/s下,經144次試驗所測得的上下游溫度差值擬合曲線如圖9所示。記環境溫度為x,上下游溫度差值為y,風速為z,若不采用補償算法,其擬合函數為:

z=(p1+p2x+p3x2+p4y+p5y2+p6y3)/

(1+p7x+p8y+p9y2+p10y3)

(4)

式中:p1=14.210 8,p2=-0.011 5,p3=6.497 4,p4=-10.888 8,p5=2.814 9,p6=-0.229 7,p7=0.002 9,p8=-0.187 0,p9=-0.128 4,p10=0.036 9。

圖9 實測數據擬合曲線圖

比較圖9與圖6曲線可知,兩者趨勢大致相同,在同一風速下,環境溫度越高,上下游溫度差值越小;同一環境溫度下,風速越低,上下游溫度差值越大,但由于實際測量中各部件間無法預測的傳熱等因素的影響,環境溫度與上下游溫度差并非呈嚴格的線性關系。如2 m/s的風速,當環境溫度從-10 ℃逐漸變化至40 ℃時,上下游溫差從4.24 ℃降為3.11 ℃,若忽略環境溫度的影響,溫漂誤差可達27%,因此本文利用遺傳算法優化BP神經網絡的算法對測量的數據進行擬合[12],便可得到環境溫度、上下游溫差與風速的關系式。

由于環境溫度、上下游溫差這兩個變量的變化范圍和單位都不同,會造成神經網絡收斂速度慢,訓練時間長等問題,因此將兩個輸入變量的范圍歸一化,映射至[-1,1]范圍內。

4 算法處理結果分析與實際測量效果

4.1 算法處理結果分析

圖10 預測值與期望值對比圖

記錄訓練好的BP神經網絡各層權值和閾值,由此得出擬合公式:

V=purelin{tansig(TWi1+ΔTWi2+ai)Wki+bk}

(5)

式中:Wi1、Wi2分別為環境溫度T和上下游溫度差ΔT對應的由輸入層到隱含層的權值,Wki為隱含層到輸出層的權值,ai、bk分別為隱含層和輸出層的閾值。因本文設定BP神經網絡為2-5-1結構,故i=1、2、…、5,j=2,k=1。Wij、Wki、ai、bk的具體值如下:

(6)

Wki=

(-1.831 2 -1.221 7 1.810 7 1.345 9 -0.857 4)

(7)

(8)

bk=-0.162 8

(9)

4.2 實際測量效果

為驗證該測風儀的性能,將該測風儀置于不同時間、不同環境溫度、不同風速下進行實際測量,且采用未經補償(式(4))與經GA—BP神經網絡補償(式(5))的兩種函數關系式測量風速。在利用該十字正交型熱溫差式測風儀測風時,主要測量參數為風速值V和風向角θ;測試時間分別選取2019年6月20日至23日的幾個不同時間點,測試地點位于南京市浦口區南京信息工程大學氣象站,標準數據由距地面5 m處的風速傳感器(EL15-1型杯式風速傳感器)和風向傳感器(EL15-2型風向傳感器)采集。

實測結果如表1和表2所示。

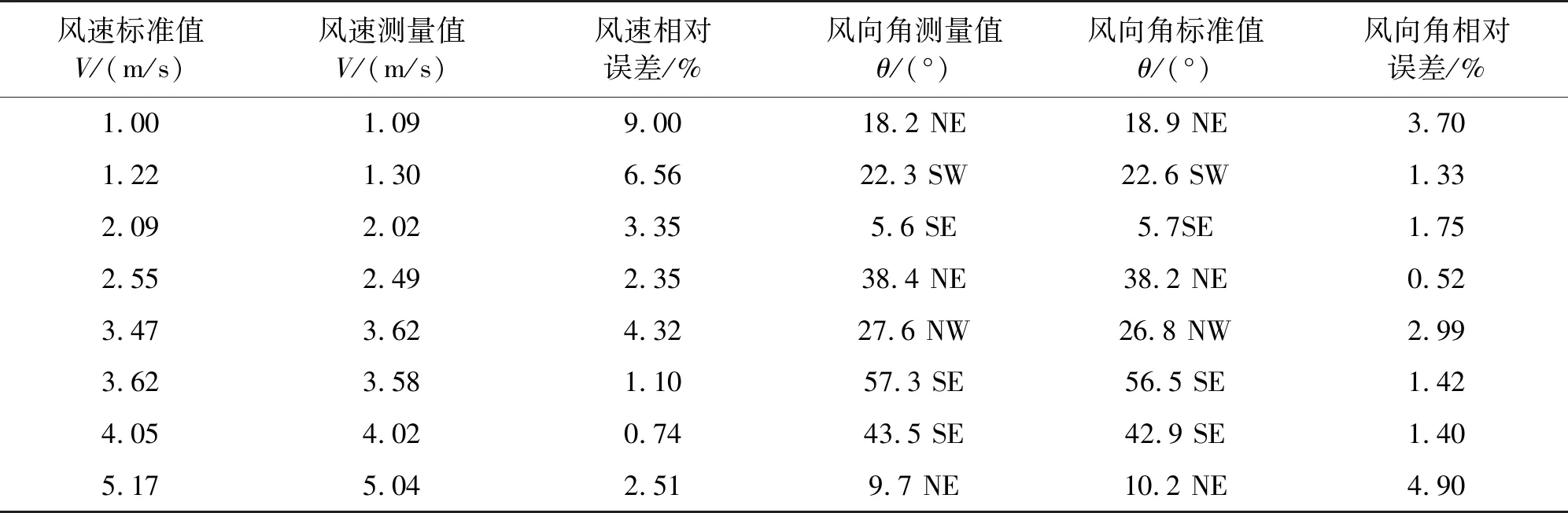
表1 風速風向實測值與標準值對比結果

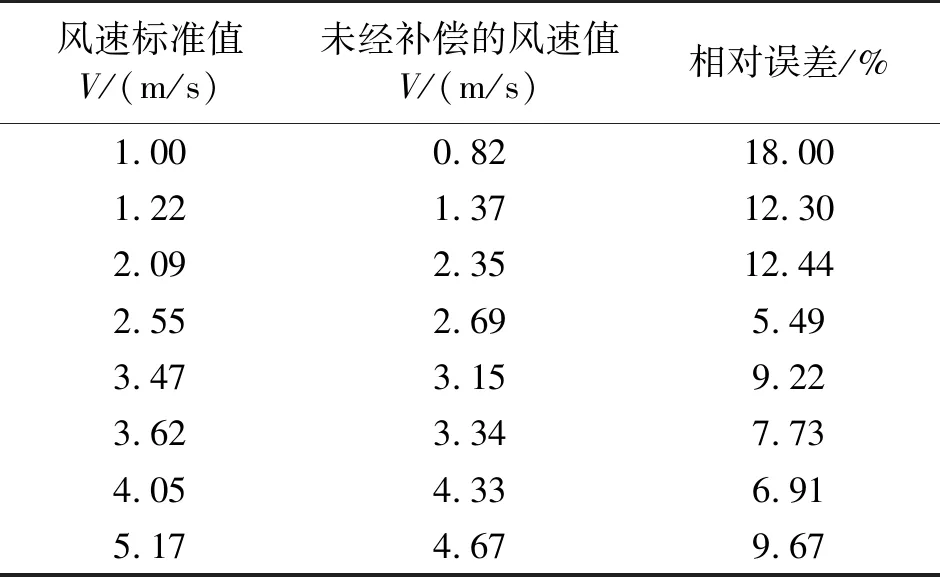
表2 未經補償的風速值與標準值對比結果

根據表1可知,十字正交型熱溫差式測風儀的實測數據和標準數據相比,雖然有所偏差,但仍在可控范圍之內,故所得的實測數據較為可靠。由于環境溫度、導管導熱以及自然界空氣中介質等的影響,導致測量值與標準值存在一定偏差,相對誤差在10%以內。實測風向角與標準風向角相比,相對誤差較小,可控制在5%以內。表2為未經補償的風速值與標準值的對比結果,其測量結果明顯劣于表1。綜上所述,十字正交型熱溫差式測風儀在實際測量中與標準值較為接近,測量效果較好,是一種可采取的新型測量風速風向的方法。

5 結論

針對目前常用測風設備存在的弊端,本文提出了一種成本低、體積小、原理簡單的風速風向測量方法,該方法根據兩根互呈90°交疊分布的導管內上下游溫度差求得風速:當有風吹過時,上游風帶走中間加熱片的熱量至下游,導致下游溫度高于上游,根據上下游溫差與風速的關系可得風速,且該設計可通過正交分解得到二維空間內任意方向的風速以及風向角。由于環境溫度對風速傳感器的影響最大可達27%,本文提出遺傳算法優化BP神經網絡算法對環境溫度造成的誤差進行補償,得到的擬合曲線函數精度較高。最終在南京信息工程大學氣象站通過實際測量驗證了該方法的有效性。

十字正交型熱溫差式測風儀還有很大的提升空間。本文設計的測風儀為十字型陣列,采用四個對稱分布的PT100溫度傳感器,在今后的研究中,可探索正方形、圓形等其他形狀陣列的測風儀,測量的效果可能更佳。另外,本文提出遺傳算法優化BP神經網絡算法對環境溫度造成的誤差進行補償,可嘗試其他算法對誤差補償,進一步提高測量精度。