大型楔形建筑風載荷數值模擬及模型尺度效應研究

孫學儒,孫 勇,吳文杰,段 峰,宋鵬超

山東農業大學 水利土木工程學院,山東 泰安271018

近年來由于全球極端氣候現象不斷增加，大風天氣往往會對大型建筑結構帶來較為嚴重的威脅，以至于大型建筑的風載荷及抗風研究一直備受關注，特別對于設計階段的分析校核上，如何快速評估建筑風載荷是否滿足設計規范的研究顯得十分重要。對于這些問題，國內外學者進行了大量研究，KIM[1]、王振華[2]等人采用基于雷諾時均方程的標準k-ε、RNGk-ε、Realizablek-ε和雷諾應力模型四種湍流模型對大跨屋蓋表面平均風壓分布進行了數值模擬，結果表明四種湍流模型的模擬結果之間差異較小；何連華[3]等人通過風洞試驗和數值模擬，對成都來福士廣場建筑群分別進行了表面風壓測試試驗及行人高度風環境的模擬研究，為主體結構設計和幕墻設計提供依據，并結合研究成果提出了改善建議；何星星[4]等人基于CFD 數值模擬方法，利用RNGk-ε湍流模型對階梯型大跨屋蓋風荷載進行了研究，并與風洞試驗結果進行對比分析，得出階梯型大跨屋蓋結構表面的風壓分布及變化規律，為同類復雜體型的大跨結構抗風研究提供依據。

建筑外形是決定氣動荷載的關鍵因素，通過合理改變建筑外形，對建筑外形進行優化設計，可以顯著改變作用于建筑結構的風荷載。余遠林[5]、謝壯寧[6]等人對不同錐度的楔形建筑模型進行風效應研究，表明適當錐度的體形可以有效消減作用于結構上的橫風向氣動荷載；鄧挺[7]等人通過試驗表明，對楔形建筑的中間層角區進行敞開處理(局部氣動措施)后，建筑結構風致荷載的消減效果明顯。雖然CFD 方法具有分析周期短，成本低且可以獲得極為豐富的流動細節等顯著優點，但是相教于模型風洞試驗可以獲得較為穩定的試驗結果不同，CFD 方法計算結果受使用不同軟件、不同湍流模型及不同網格等因素影響較為劇烈；因此使用CFD 方法分析實際問題需要很多的實際計算經驗和必要的計算驗證；在實際工作中一般選擇已有試驗結果作為CFD 驗證的數值基準，通過比較CFD 計算結果同試驗的差距來判定數值計算方法是否可靠及適用。對于超大型建筑，風洞試驗往往只能在模型尺度下完成，而直接將模型試驗的結果應用在實際尺度上是否恰當有待商榷，而CFD 方法可以在滿足計算機計算能力的基礎上分析不同模型尺度的計算結果。

1 試驗及數值分析模型

1.1 試驗概況

本文的研究對象為泰山文化藝術中心，主體建筑高31 m，屋頂最高點40.9 m，總占地38558 m2，屋頂結構可以分為A 區、B 區屋頂和C 區頂棚，如圖1。風洞試驗在中國建筑科學研究院風洞實驗室完成，該風洞為直流下吹式風洞，全長96.5 m，包含兩個試驗段。試驗在高速試驗段進行，試驗段尺寸為4 m 寬、3 m 高、22 m 長，風速在2 m/s 到30 m/s 連續可調。風洞外觀如圖1；根據風洞阻塞度要求、轉盤尺寸及原型尺寸，試驗模型縮尺比確定為1:150，試驗在B 類地貌下進行，取風剖面指數α=0.16；參考高度取350 m，試驗風速為16 m/s。在風洞中采用尖劈配合粗糙元的方法模擬得到的風速剖面。模型根據建筑圖紙準確模擬了建筑外形，以反映建筑外形對表面風壓分布的影響。

圖1 風洞試驗模型Fig.1 Model of wind tunnel test

圖2 CFD 分析模型Fig.2 Model of CFD analysis

1.2 數值計算模型及邊界條件

為了準確模擬實際模型試驗場景，CFD 驗證分析所采用的幾何模型同試驗模型尺度相同、幾何相似，具體模型如圖2。入口邊界條件同試驗保持一致，CFD 模型的邊界條件設置見表1；計算域寬度和高度同風洞試驗尺寸相同，長度為模型前方2H 為速度入口，模型后方5H 為壓力出口(H 為建筑高度)。

入口速度分布采用了一般速度入口邊界條件，平均風速剖面和湍流風剖面通過編寫場函數定義，風洞試驗及CFD 分析入口平均風剖面分布如圖3（a）；CFD 分析一般入口湍動強度分布如圖3(b)。

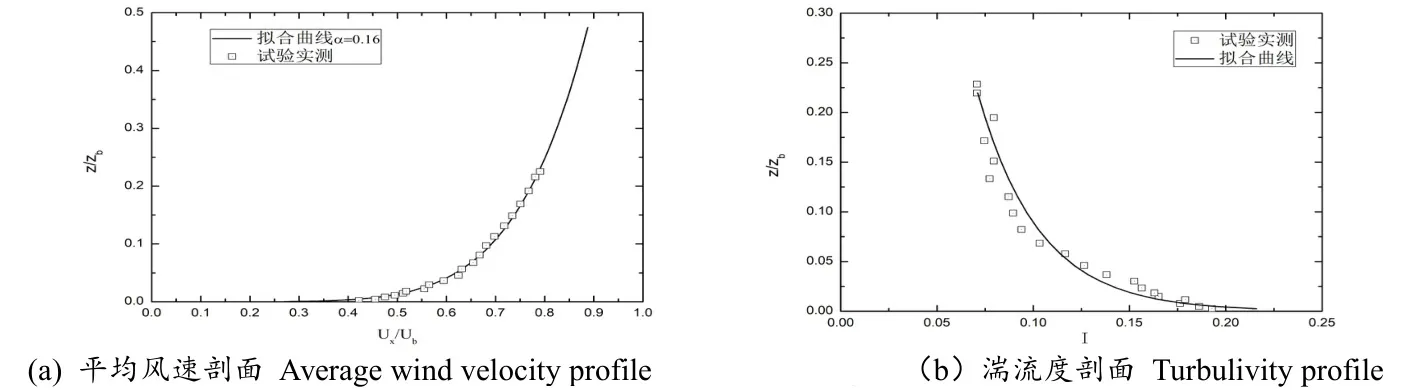
圖3 平均風速及湍流度剖面Fig.3 Profiles of mean wind velocity and turbulivity

表1 邊界名稱及邊界條件Table 1 Boundary names and conditions

1.3 網格劃分及湍流模型的選取

CFD 計算中空間離散如圖4，為了精確模擬幾何周圍流場，對模型周圍及尾流5 度范圍加密。

計算選擇瞬態的SST（Menter）k-ω湍流模型[9]，建筑壁面選擇生成6 層邊界層，以使棱柱層網格同六面體網格之間過度均勻，通過調整邊界層內層厚度，控制建筑壁面邊界層處Y+值處于80～300范圍[10]。計算域空間離散網格數量達到了350 萬。

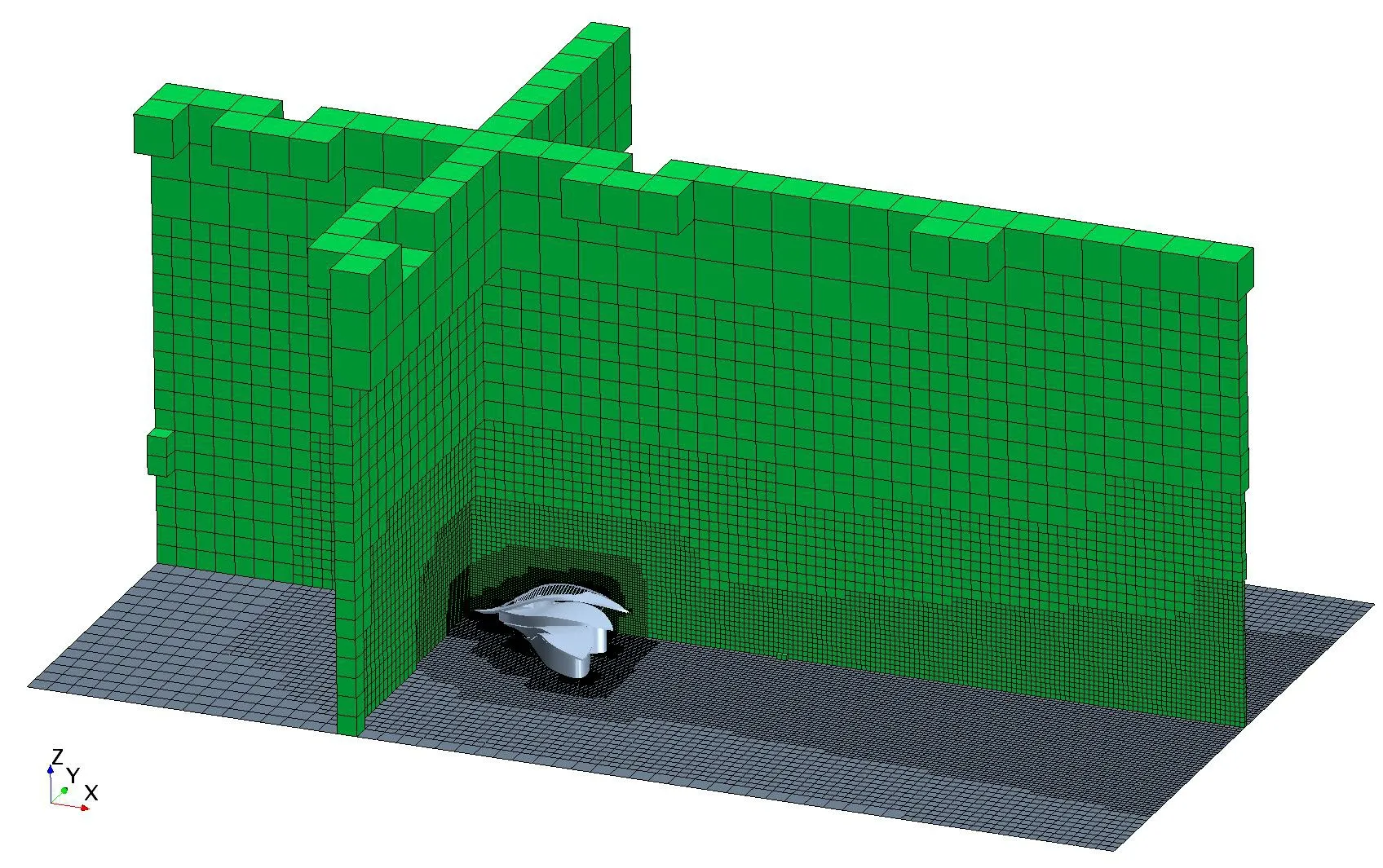
圖4 CFD 分析網格及網格加密方式Fig.4 CFD analysis grid and encryption

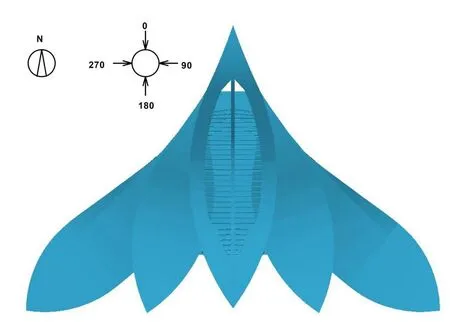
圖5 風向角定義Fig.5 Definition of wind direction angle

1.4 風向角定義

風向角的定義如圖5 所示；風洞試驗一共完成了36 個風向角（每隔10 度）的試驗測試；CFD分析為了驗證數值計算方法的可靠性，對不同風向角工況進行了相應的數值模擬。為了驗證CFD 計算所得建筑表面平均壓力系數結果是否準確，在建筑表面上選取了6 個關鍵點，通過將試驗結果同CFD 計算結果所得6 個關鍵點的平均壓力值進行比較，驗證CFD 方法的計算精度，為后文分析尺度效應尋找一個合適的數值計算方法。這6 個觀測點的具體位置如圖6，建筑外表面左右對稱，監測點均分布在東部建筑表面，其中P1～P3 分布在建筑C 區頂棚上，P1 為頂棚的最北位置，P2 為頂棚最高位置，P3 為頂棚的最南位置；P4 為B 區屋頂上表面最南位置；P5 為A 區屋頂上表面最南位置，P6 為幕墻中間高度位置（曲面曲率最大位置）。

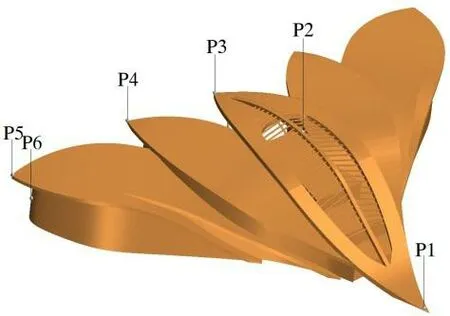
圖6 平均壓力系數觀測點分布Fig.6 Observation point distribution of mean pressure coefficients

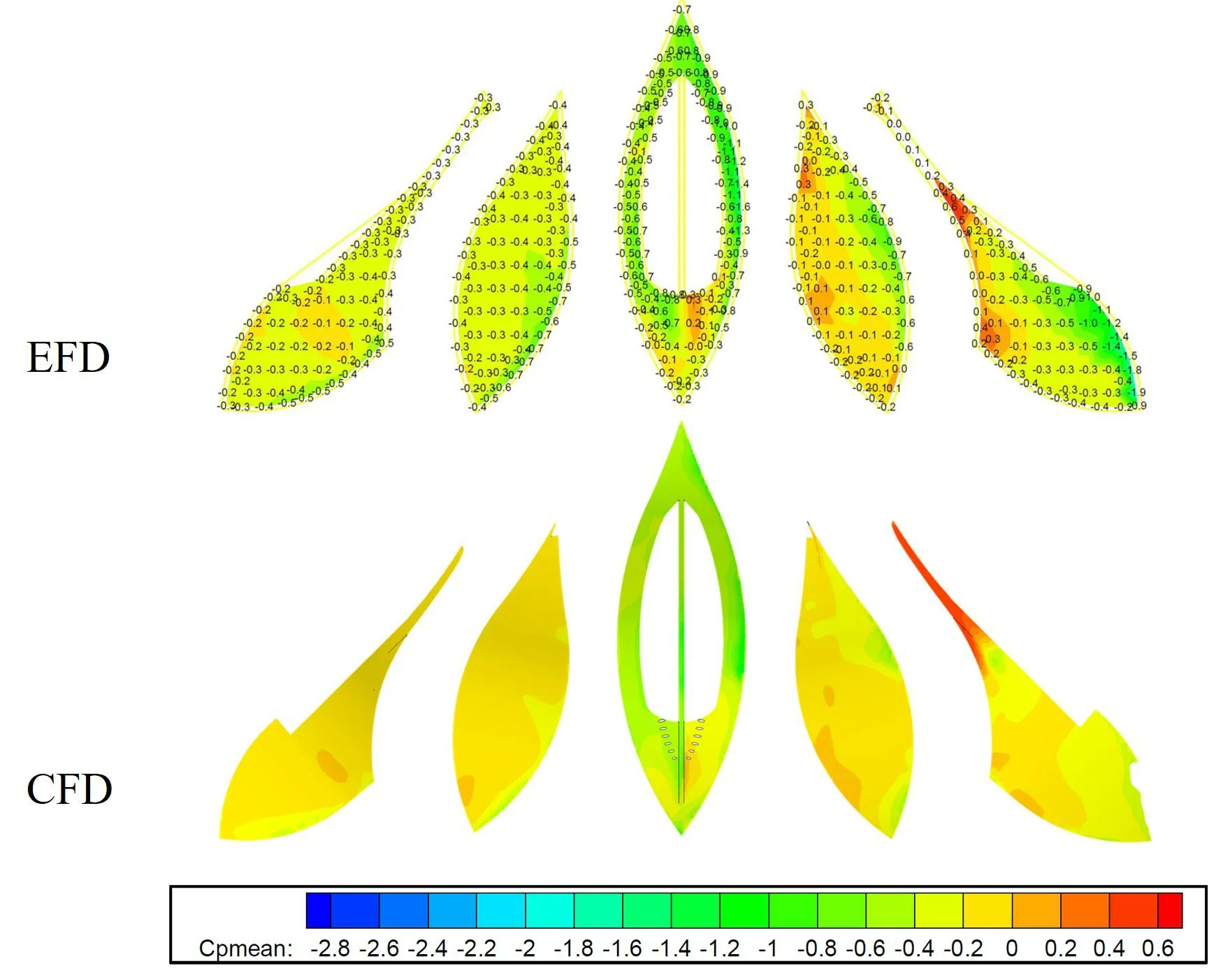
圖7 建筑表面的壓力分布云圖（90 度風向角）Fig.7 Pressure distribution cloud picture on the surface of the building(Wind direction angle at 90°)

1.5 風壓結果分析

圖7 是90 度建筑表面的壓力分布圖；上部分EFD 表示風洞試驗結果，下部分為CFD 計算結果。圖8 是0 度級及180 度風向角建筑表面的壓力分布圖；其中左邊為風洞試驗結果，右邊為CFD 計算結果；如果僅分析壓力分布圖，有以下結論：1）在四個不同的風向角下，風洞試驗結果及CFD 分析結果建筑表面壓力分布趨勢比較接近；2）四個不同風向角下，風洞試驗及CFD 分析結果的平均壓力系數極值大小比較接近，圖9（a）中壓力最大值出現在正北方，大小接近0.8，模型試驗及CFD計算吻合良好；3）一些表面壓力變化劇烈位置模型試驗同CFD 計算結果壓力大小及分布存在一定偏差，如圖8 西測A 區屋頂，CFD 計算結果同模型試驗結果存在一定偏差。在本文中，平均壓力系數Cp的定義見式：

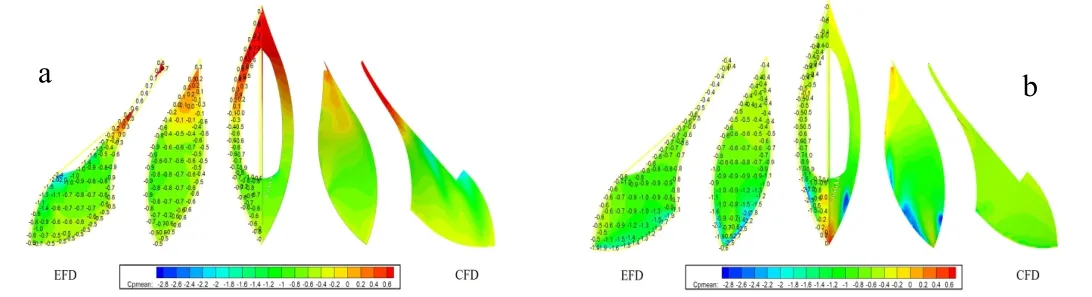
圖8 建筑表面的壓力分布云圖Fig.8 Pressure distribution cloud picture on the surface of the building

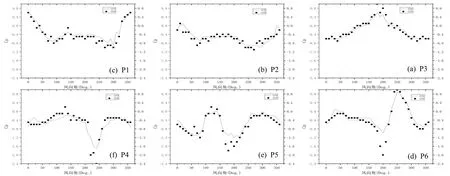
圖9 監控點平均壓力同風向角的函數曲線Fig.9 Function curve of average pressure and wind direction angle at the monitoring point

監控點平均壓力系數隨不同風向角的變化曲線如圖9 所示。其中的P1～P3 點屬于頂棚上的三點，實際風洞試驗及CFD 計算結果均比較穩定且兩者吻合良好；而P4～P5 點由于屬于下層屋頂，流場受到建筑本身干擾較大，且測量監控點位于屋頂邊緣位置，這樣給測量及計算帶來了不穩定性，導致測量及CFD 分析結果極值存在較大偏差，P4 點在240 度風向角平均壓力系數誤差值達到0.8，P5 點在180 度風向角平均壓力系數誤差值達到0.7；P6 點位于流動分離位置，受到風向角的影響較為劇烈，同時P6 點處于流動分離位置，存在較大的速度梯度，這樣也容易導致測量及CFD 計算誤差。

但是從圖8 及圖9 中可以看出，雖然建筑表面的某些位置CFD 計算的壓力系數同試驗結果的壓力系數在數值上存在一定的差異，但是從分布趨勢看，總體吻合良好。

總結以上分析，認為本文所采用的數值計算方法是較準確的，可以用于后續分析。

2 尺度效應模擬及分析

2.1 計算模型及縮尺比

本部分采用前文通過驗證的數值計算方法，完成對大型楔形建筑風載荷尺度效應的研究。計算模型同前文采用的數值模型主尺度相同，但是考慮到不必要的建筑細節會導致計算網格的激增且還會帶來不必要的流場擾動，因此對前文計算模型進行了一定簡化；如圖10 所示，風向角的定義同前文相同，由于本部分僅分析尺度效應作用，故除去了風向角的影響，僅分析了風向角為零的情況，并且在計算過程中，由于建筑和邊界條件左右對稱（從零度風向角方向上看），故CFD 分析僅計算半個模型，中間采用對稱面邊界條件處理。

計算采用的縮尺比及具體網格數量見表2；本部分一共分析了6 個不同的縮尺比。

表2 尺度效應分析模型編號及網格數量Table 2 Scale effect analysis model number and grid number

圖10 尺度效應分析計算模型Fig.10 Scale-effect analysis and calculation model

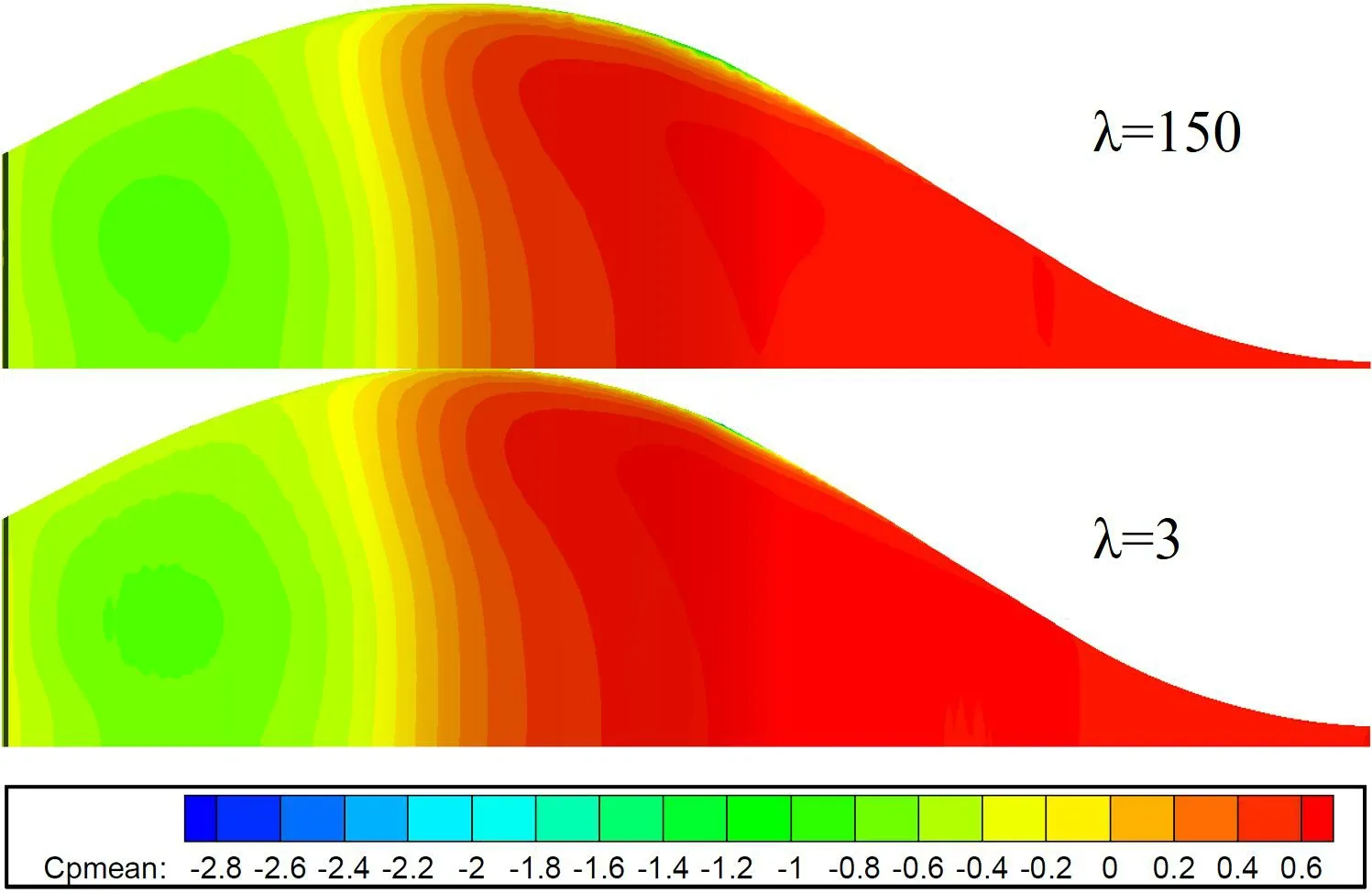
圖11 不同縮尺比建筑表面壓力分布Fig.11 Surface pressure distribution at different scale ratios

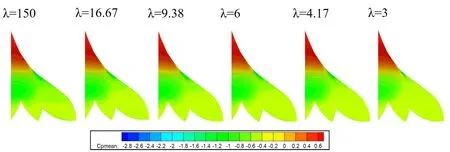
圖12 不同縮尺比建筑表面壓力分布Fig.12 Surface pressure distribution at different scale ratios

2.2 尺度效應結果分析

圖11 表示縮尺比分別為150 及3 時正東方向視圖建筑表面壓力分布，圖12 為分析的六個不同縮尺比情況下屋頂表面平均壓力分布。比較圖11 及圖12 中不同縮尺比情況，分析發現建筑表面平均壓力分布及大小均十分相似；初步結論認為建筑表面的平均壓力系數受尺度效應的影響比較微弱。

圖13 表示建筑中剖面（從來流方向上看）流場來流方向的速度分布，圖14 為建筑后方x/L=1.1平面（平面與遠場來流速度方向垂直）速度分布云圖。圖13 中，觀察速度小于3 m/s 的流場分布區域，發現縮尺比為150 時速度小于3 m/s 的區域從建筑尾部一直延伸到x/L=1.4 位置；縮尺比為6 時速度小于3 m/s 的區域從建筑尾部延伸到x/L=1.3 位置，而縮尺比為3 時速度小于3 m/s 的區域從建筑尾部延伸到x/L=1.2 位置。從建筑對尾部流場的尾流范圍的影響上看，尺度效應十分明顯。圖14同樣佐證了這一點，在圖14 中，尾流速度分布范圍存在較大區別，同時，尾流速度在相同位置大小也存在較大區別，圖14 中紅色箭頭標記位置，在縮尺比為150 時，流速最小值為-2 m/s 左右，縮尺比為6 時，流速最小值為-2.6 m/s 左右，縮尺比為3 時，流速最小值為-4 m/s 左右。可見，尺度效應對建筑尾部流場的流場分布及流場流速大小分布均具有較大作用。

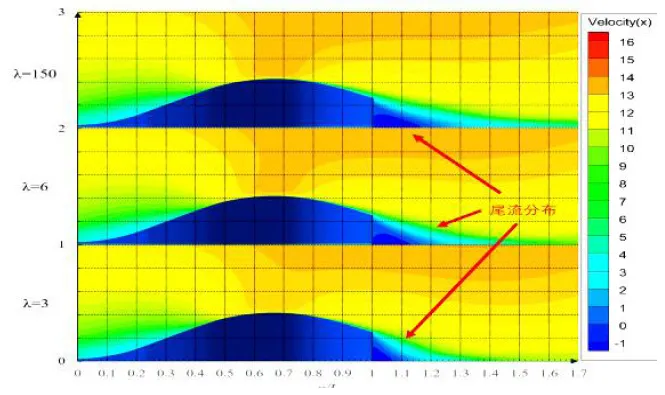
圖13 建筑尾流分布（縱中剖面）Fig.13 Building wake distribution(longitudinal section)

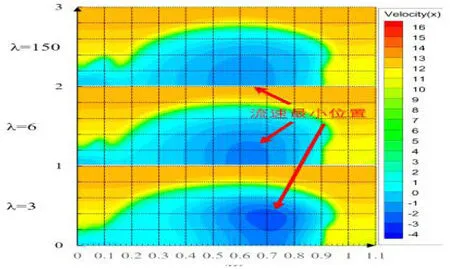
圖14 建筑尾流分布（橫剖面）Fig.14 Building wake distribution(transverse section)

3 結語

（1）CFD 數值分析方法作為當前流行的設計及分析工具，越來越受到科技工作者的重視。其優勢眾多，如低設計成本、較高分析精度，并且可以提供完整的流場分布結果。如本文風洞試驗一般盡可測量某些固定點位置的瞬時壓力，但是測量點的數量受到傳感器數量的限制，并且風洞試驗較難得到流場完整的速度分布結果，而采用CFD 分析方法可以較精確的獲取整個流場的壓力及速度分布結果；并且目前常規電腦工作站的計算性能已經能夠處理上千萬的CFD 計算網格，這對CFD 在結構風工程的應用奠定了硬件基礎。本文的第一部分驗證了CFD 計算方法的準確性，通過本文使用的CFD 分析方法可以較精確的求解建筑表面壓力分布。

（2）通過本文CFD 分析發現，尺度效應對建筑物表面的壓力系數的影響有限，如果僅考慮建筑表面壓力分布，尺度效應或者雷諾數的影響可以忽略，即對于大型建筑，僅僅分析較小的模型尺度也具有較高的分析精度。但是，如果需要考慮建筑尾流壓力及速度分布，尺度效應或者雷諾數則對建筑尾流速度和壓力分布影響較大。本文僅分析單體建筑，如果考慮群體建筑，或者分析建筑之間相互影響，則需要重點考慮尺度效應或者雷洛數的具體影響。