引風機電機改造變頻運行時軸系系統扭振的分析及處理

張 菁

(上海電氣集團上海電機廠有限公司，上海 200240)

0 引言

引風機是電廠的三大風機之一，在運行中若出現問題，會造成機組風量不夠，影響電廠發電的穩定運行。某電廠3#機組兩臺引風機希望進行變頻節能運行改造：利用原YKK900-8 5 100 kW 6 kV工頻運行過的電機和變頻器及相應的傳感器形成閉合回路，根據發電量所需風量調整引風機轉速。該廠直接將普通工頻電機、變頻器、引風機相連運行，未做軸系上的匹配分析，存在不確定風險因素。這種沒有從系統性角度去考慮，直接將各單元設備裝配使用的改造情況在行業內時有發生，主要原因是業主對轉動部件的軸系系統了解不夠。因此，針對該情況，我公司為引風機電機變頻節能運行改造的軸系中扭振問題做了系統分析。

1 引風機改造系統各設備參數情況

電機參數為

異步電動機額定功率：5 100 kW

額定電壓：6 kV

額定轉速：745 r/min

轉子轉動慣量：910 kg·m2

額定轉矩：66 kN·m

電機極數：8極

引風機轉動慣量：5 400 kg·m2

變頻器參數為

變頻器容量：6 200 kVA

額定電壓：6 kV

額定電流：596 A

開關頻率：800 Hz

升速時間：0～20 Hz(60 s)，20～50 Hz(60 s)

降速時間：0～20 Hz(60 s)，20～50 Hz(100 s)

2 分析和計算

引風機與電機、變頻器、傳感器設備，形成一個閉環系統，如圖1所示。

圖1 風機節能系統功能圖

該軸系系統可能存在一些影響軸系扭轉振動的因素：第一，變頻器根據計算器輸入的數據進行變頻調整，從發電量側檢測數據若停留在某個波動范圍內，則變頻器容易出現頻繁的在某一頻率范圍內細微波動，頻率時上時下，此時容易形成交變應力，因此調速系統需有一定的延遲性；第二，當整個系統軸系和變頻器中電能輸入電頻率產生共振，則會出現機電諧振現象，這種情況我們也要分析，并且避免此類現象出現；第三，該系統軸系中縱向振動也存在一定的可能，此文不做分析。

2.1 電動機軸分析計算

2.1.1 電機軸疲勞強度安全系數極核

該電機原為工頻運行下的引風機電機，功率5 100 KW、電壓6 KV、轉速745 r/min、轉子重量7 000 kg。軸材料采用16 Mn，抗拉強度σb：500 MPa，屈服強度σs：295 MPa。根據軸系圖和受力分析繪制的彎矩圖和扭矩圖，如圖2所示。

圖2 彎矩和扭矩圖

圖2可看出軸伸段的扭矩最大。鐵心段的彎矩最大，抗彎矩斷面模量在鐵心段最大，所以此段彎矩應力較小。通常電機驅動端軸承檔處軸徑較小，兩側軸肩導圓角過渡，則此處斷面模量較小和應力集中。根據材料力學和經驗可以得出該軸危險斷面處可能在驅動端軸承檔靠近鐵心側。下面計算該斷面處設計強度是否滿足電機運轉要求，此時：

F1=33 946 N；F2=33 954 N；軸伸軸承檔中心與軸軸肩間距L=110 mm；軸承檔直徑d=220 mm；圓導角r=4 mm。

彎矩M=F1×L=3 734 060 N·mm；

相對交變應力下的彎矩疲勞限值σ-1=0.27(σb+σs)=214.65 MPa

相對交變應力下的扭轉疲勞限值τ-1=0.156(σb+σs)=124.02 MPa

查尋相關系數表：

圓導角處有效應力集中系數kσ=1.95；kτ=1.61

絕對尺寸干涉系數εσ=0.6；ετ=0.6

軸承檔軸段表質量系數β=1

彎矩和扭轉時的類比系數ψσ=0.1；ψτ=0.05

則，安全系數計算如下：

(1)

(2)

加工軸時圓導角r=2 mm，此時查相應的圓導角處應力集中系數表有：kσ1=2.13；kτ1=2.19

計算安全系數得：

(4)

(5)

綜上所述，上述電機軸的軸承檔處軸段疲勞強度安全可靠。

2.1.2 YKK900-8電機轉子固有頻率分析

采用ANSYS13.0有限元計算軟件轉子動力學模塊對轉子系統進行模態分析。

YKK900-8電機轉子為剛性轉子，一階臨界轉速遠遠偏離于電機工頻運行轉速，工頻運行時沒問題，但是該電機若做變頻運行時應避開34.4 Hz和39.2 Hz。

2.2 變頻器

引起交變應力的原因主要有兩個：第一，由于系統的調速需要，DCS不斷調整變頻器的運行頻率引起電動機和風機的轉速交變，使電動機與風機的軸系受到交變應力；第二，由于變頻器輸出的電壓中含有少量的高次諧波，諧波電壓會引起電動機產生諧波電流從而在軸系上產生脈動轉矩。

2.2.1 升降速時的轉矩變化

首先來計算頻繁調速時，軸系承受的轉矩情況，根據電機拖動的運動方程：

(7)

根據以上計算，在變頻調速過程中，變頻器控制電動機提供的電磁轉矩變化量及交變轉矩僅僅為0.7%和0.46%，調節的頻度跟DCS給變頻器的指令有關。

圖3是電動機自由墮走和變頻器拖動降速時的曲線。由于風機屬于平方轉矩負載，在轉速高的時候，負載的阻力大，降速比較陡，轉速比較低的時候降速比較緩，而變頻器降速時按照固定斜率的直線降速。圖中t0是開始降速的時刻，兩條線的交點是在t1時刻，在t0到t1之間，風機自由降速的速率比變頻器拖動降速時快，所以變頻器是托著風機在降速，此時變頻器處于拖動狀態，在t1到t2這段，風機降速較慢，變頻器是拖著風機降速，此時變頻器處于輕微制動狀態，電動機由于轉子磁場轉速高于定子磁場轉速，變成了發電機，向變頻器充電[1]。但變頻器是只能工作在一三象限，不能向電網回饋能量，所以如果制動太快，變頻器會被充電至過壓保護。一般在調試時，降速曲線是按照變頻器不報故障設計，所以變頻器對負載的制動作用非常小。

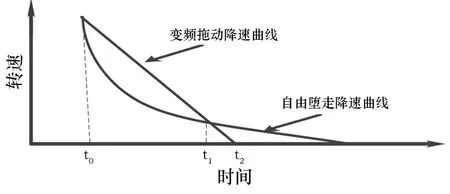
圖3 自由墮走和變頻拖動的降速曲線

2.2.2 結論

根據上述分析可知，在按照變頻器設定升降速曲線的運行方式下，有以下結果：

(1)在升速的全階段，電磁轉矩始終大于負載轉矩約500 N·m，與實際計算的結果較為符合；

(2)在降速的全階段，電磁轉矩始終小于負載轉矩約283 N·m，與實際計算的結果同樣較為符合；

(3)在運行到279 s即降速149 s時，電磁轉矩過零，此后的11 s降速時間內電磁轉矩為負值，最大達到-390 N·m。

(4)電磁轉矩過零的時刻電機轉速已下降到3.7 Hz，而真實運行工況一般不會在此頻率點來回頻繁調速，故可得出結論為：按照一般工況的常用調速區間(20～40 Hz)內，不會出現電磁轉矩為負的情況。

2.2.3 變頻器的諧波分析

由出廠試驗波形可以看出，變頻器輸出AB電壓諧波THD最大為2.09%，其中主要諧波次數和最大值見表1：

表1 AB電壓諧波THD

由出廠試驗波形可以看出，變頻器輸出BC電壓諧波THD最大為2.11%，其中主要諧波次數和最大值見表2：

表2 BC電壓諧波THD

注：由于變頻器出廠試驗僅測試兩個線電壓，所以沒有AC線電壓的波形和數據。

在變頻器拖動電動機空載時，主要諧波次數為5次，約1%。

2.2.4 變頻器諧波引起的脈動轉矩分析

由于變頻器輸出的諧波在電動機上產生的脈動轉矩計算較復雜，此處采用仿真的方法，按照變頻器輸出的實際波形(含諧波)加到電動機模型上，觀察脈動轉矩的情況，仿真模型如圖4所示[3]。

圖4 基于matlab的脈動轉矩仿真模型

輸出線電壓為6 KV，相電壓峰值約5 000 V；

空載相電流有效值約為157 A；

滿載相電流有效值約為580 A；

理想空載電磁轉矩約為0，且無任何脈動。

按照該模型，將電壓波形按照實際變頻器的諧波含量，進行仿真，輸出線電壓基波有效值約6 kV。

理想空載電磁轉矩在0上下波動，峰值為+910 N·m和-900 N·m

額定負載時電磁轉矩在65 000 N·m上下波動，峰值為+65 970 N·m和-64 260 N·m，即脈動轉矩的峰值為970 N·m和-740 N·m，脈動轉矩的有效值為60 N·m和-46 N·m。

2.2.5 結論

根據上述分析可知，在完美無諧波條件下，無論空載、滿載，電壓電流波形均正常，電磁轉矩無脈動。而根據變頻器出廠試驗波形中的諧波含量表設置的仿真條件下，則有：電機及風機系統存在轉矩脈動，但波動的峰值不超過±60 N·m，為額定轉矩的0.092%；加載前后，電磁轉矩脈動幅值基本相同，說明脈動轉矩只與電壓諧波的幅值有關，與負載無關；電磁轉矩脈動的諧波頻率為基波的4、6、8、12、14、16次。

2.3 風機計算

該電廠5#爐引風機改造計劃中的電機及風機軸系扭振固有頻率計算結果如下：

一階機械轉速頻率14.66 Hz，對應4次諧波電頻率為58.64 Hz；

二階機械轉速頻率29.29 Hz，對應4次諧波電頻率為117.16 Hz；

三階機械轉速頻率220.92 Hz，對應4次諧波電頻率為883.68 Hz。

2.3.1 扭轉振動的特性

根據有阻尼作用的扭轉振動[4]，有以下公式：

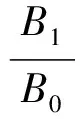
(1)軸系固有頻率fn與軸系的慣量和軸系柔度有關，柔度增大則固有頻率減小；

(2)當扭轉振動在激振源的作用下，不論軸系阻尼系數強弱，扭轉振動頻率與激振源頻率一致時，扭轉振動激振力矩會不斷疊加，進而產生很大的振動幅值，這個振動幅值會使軸的材料出現疲勞，使軸的柔度變大，進一步對軸造成損傷；

(3)激振力矩是產生扭轉振動的源頭，它的數值與扭轉振動幅值相關；

(4)軸系阻尼系數起減弱振動幅值的作用，阻尼系數變大，振動幅值變小；

(5)當扭轉振動受幾個不同振動幅值和頻率的振動力矩時，用矢量相加原理進行分析。

2.3.2 扭轉振動建模

電動機與引風機的連接示意如圖5所示[5]。

圖5 電動機與引風機連接示意圖

將電機轉子與風機連軸運行等效為雙體系統的振動模型。雙體軸系振動模型在無阻尼振動中，兩個旋轉體都在進行簡諧振動，它們的振動頻率和相位都相同。

扭轉振動中有兩種振動方式：第一，類似于連接軸為剛性，兩個物體的扭轉振動幅值相同。第二，兩個物體的扭轉振動幅值比等于轉動慣量的反比，根據物體的質量越大則慣量越大，那么慣量大的那個物體振動幅值小，此時兩個物體振動幅值方向相反，因此軸系上必然存在一節點的振動幅值為零，此處應力最大，軸系損傷通常出現在該節點上。這就是為什么軸系共振發生斷軸時多出在軸承檔處，因為軸承檔處軸段是整個軸系最薄弱的地方。

3 結果分析

根據以上計算情況，有以下結論：

(1)根據電機軸疲勞強度安全系數的計算，安全系數滿足要求。

(2)電機的水平方向一階固有頻率為34.4 Hz，垂直方向一階固有頻率為39.2 Hz(這在工頻50 Hz運行的條件下可以避開，但當變頻運行時就需注意避開這兩個固有頻率)。

(3)變頻器輸出電壓諧波主要為5～17次的奇次諧波，總的THD約為2.1%，滿足國標4%的要求。

(4)按變頻器設置的升降速時間，升速時軸上的動轉矩為503 N·m，降速時動轉矩為302 N·m，分別為電動機軸額定轉矩的0.7%和0.46%，符合要求。

(5)根據變頻器的諧波結果，使用仿真的方法，得到在脈動轉矩的幅值最大為：有效值±60 N·m，約為額定轉矩的0.1%，電磁轉矩脈動的主要諧波頻率為基波的4、6、8、12、14、16次。

風機與電動機軸系的固有頻率為：

一階機械轉速頻率14.66 Hz，對應4次電頻率為58.64 Hz；

二階機械轉速頻率29.29 Hz，對應4次電頻率為117.16 Hz；

三階機械轉速頻率220.92 Hz，對應4次電頻率為883.68 Hz。

綜上所述，該改造計劃中，工頻電機與風機連接的軸系，在設定運行工況下存在一定運行風險，根據計算結果，初步判斷為軸系的二階固有頻率117.16 Hz與變頻器運行頻率(25 Hz左右)的五次諧波(約125 Hz)接近，會出現軸系的扭振共振風險，出現很強的交變應力快速使軸系達到疲勞壽命而損壞風險。根據雙體系統的振動模型，軸系危險處應該電機驅動端軸承檔處或者風機側軸承檔處，此處需做加固處理，此處的軸徑也需加強。

4 處理措施

(1)根據計算結果，變頻器不適合長期運行在20～30 Hz頻率段，變頻器設置參數跳過該頻段和25 Hz、34.4 Hz、39.2 Hz。

(2)采用儀器測量的方法測量軸系的扭振情況，找出扭振的固有頻率點，與計算結果進行驗證。

(3)為了減小升降速對軸系帶來的交變應力，在DCS上只允許變頻器運行在30 Hz、42 Hz、45 Hz、50 Hz幾個點，同時由風機靜葉配合調節負壓。

(4)在3#引風機變頻節能改造計劃中，電機最好使用變頻電機，特別是提高軸的剛度，減小軸系柔度，另外根據雙體系統的振動模型，應將電機軸和風機軸，軸承檔處的軸徑和軸肩倒角增大處理，避免應力集中，且軸徑也需相應增大。

(5)在條件允許情況下，在軸系上安裝扭振監控設備，實施對扭振大小進行監控，在出現扭振幅值偏大時自動調整運行頻率。

5 結語

在工業電機驅動系統中，像上述情況進行風機改造變頻運行時，應注意核算軸系的固有頻率，而不是簡單將變頻器、工頻運行電機、風機連接形成閉環調速系統即可。在調速系統上或許沒問題，但是軸系在變頻運行上存在共振、扭振的風險。需對整個軸系進行分析，一般至少分析整個軸系1、3、5階臨界轉速，如果調速范圍比較寬，電機變頻范圍廣的，需計算更多階的臨界轉速。同時，變速系統中所使用的電機需特殊設計，軸的材料提高剛度。然后再按軸系臨界轉速的范圍設置調速范圍，將共振點避開運行。