高空長航時無人機螺旋槳后掠槳葉氣動研究

馬成宇,何國毅,王 琦

(南昌航空大學 飛行器工程學院,南昌 330063)

0 引 言

螺旋槳是指通過槳葉旋轉推動氣流加速運動從而產生推力的動力裝置。在噴氣動力之前,螺旋槳是航空飛行器的主要動力系統(tǒng),即便在世界航空史進入噴氣動力時代之后,螺旋槳以其高效、經濟的優(yōu)勢依然是部分航空飛行器首選的動力裝置[1-2]。但由于螺旋槳槳尖馬赫數的限制,傳統(tǒng)的螺旋槳無法在高亞音速范圍內高效工作,因此對于螺旋槳的應用及設計很長時間只停留在低速范圍內。為提高螺旋槳的槳尖臨界馬赫數,早在20世紀50年代,槳尖后掠的螺旋槳槳葉就已出現[3],20世紀70年代美國率先開展了先進螺旋槳計劃,從氣動、結構、噪聲等方面對后掠槳葉進行設計和計算[4-6],法國,英國等歐洲各國相繼開展高速螺旋槳的研究,前蘇聯也取得顯著的成果,烏克蘭D-27發(fā)動機上所安裝的槳葉是后掠槳葉實際應用的典范[7-8]。到目前為止,多數投入使用的螺旋槳都考慮到了后掠設計,但由于對飛行速度沒有過高要求,所設計的螺旋槳槳葉只是輕微的后掠,同時由于當前使用渦扇發(fā)動機執(zhí)行高速飛行任務所用成本在可接受范圍之內,因此對螺旋槳高速性能的研究鮮有報道。

近年來,隨著人類對空域的不斷探索,高空長航時無人機逐漸成為各國研究熱點。高空長航時無人機是指飛行高度不低于18 km,飛行時間不少于24h的戰(zhàn)術或戰(zhàn)略無人機[9],相對于軌道衛(wèi)星,其成本較低,可隨時更改航線,機動性強,且飛行高度較低,偵察圖像分辨率高,可廣泛應用于空中預警、通信中繼、電子干擾、攔截戰(zhàn)區(qū)彈道導彈、海岸與邊界巡邏、大氣環(huán)境研究和空中交通管制等,被人們稱為“大氣層人造衛(wèi)星”[10-11]。根據其任務要求,高空長航時無人機對能量來源和推進系統(tǒng)有較高要求:首先,長航時的設計要求,使得無人機的供能系統(tǒng)必須能夠長時間地供應能量,同時推進系統(tǒng)必須具有較高的經濟性以減少能量消耗;其次,無人機要爬升到一定高度執(zhí)行任務,要求推進系統(tǒng)能夠保證無人機具有良好的爬升能力[12],盡量縮短爬升時間;此外,由于無人機的任務航線可隨時更改,這就要求無人機具有較好的機動能力,可以很快到達指定的任務區(qū)域,到達指定區(qū)域后又能以較低的飛行速度執(zhí)行偵察、監(jiān)視等任務,因此推進系統(tǒng)還需具備寬工況的特性。高空長航時無人機按照能量來源的不同可以分為:常規(guī)動力無人機、太陽能動力無人機、氫動力無人機和混合動力無人機。其中常規(guī)動力無人機通常選用燃油動力或者化學電池電動系統(tǒng),難以滿足長航時的設計要求;而太陽能動力無人機通常采用超大展弦比輕質結構[13-14],同時受限于天陽能轉化率低的限制,只能夠低速續(xù)航,無法滿足快速機動的設計要求;氫動力無人機因航空用燃料電池具有轉化率高、功重比高和能量密度大等特點[15-17],同時在結構設計方面與太陽能動力無人機相比不需要超大展弦比設計,使得無人機結構較強,可以達到較高的飛行速度[18];此外,采用氫能/太陽能混合動力作為供能系統(tǒng),綜合兩者供能方式的長處,是最有潛力滿足長航時和寬工況設計要求的供能系統(tǒng)[19-20]。對于推進系統(tǒng)的選擇,螺旋槳因其在低速范圍內的高效性可作為高空長航時無人機的推進系統(tǒng),以滿足高空長航時無人機慢速飛行對某一特定目標進行監(jiān)視和細節(jié)辨認的要求,同時由于螺旋槳的經濟性,易于無人機長航時飛行。唯一不足的是螺旋槳高速性能不佳,同時考慮到高空空氣稀薄,不利于散熱,高空無人機一般采用傳動結構較為簡單的定距螺旋槳[21],當飛行速度在偏離設計點之后螺旋槳效率下降很快。

目前國內外的專家學者對高空無人機螺旋槳的研究主要集中在抑制槳葉氣流分離[22-25]、螺旋槳與機翼氣動干擾[26-27]以及在設計飛行速度下螺旋槳槳葉設計[28-29]三個方面,而對如何加寬螺旋槳的有效工作范圍,增強快速爬升和機動能力研究甚少,因此針對這一問題,本文將槳葉后掠的設計思想應用到高空長航時無人機螺旋槳的改進設計上,探究槳葉后掠角對螺旋槳氣動性能的影響規(guī)律,研究結論同樣對工作于傳統(tǒng)高度內的螺旋槳提高其高速性能具有借鑒和指導意義。

1 槳葉物理模型說明

1.1 槳葉建模方法說明

本文所用無后掠槳葉數據取自文獻[11],螺旋槳半徑2.3 m,設計巡航馬赫數為0.4,基本葉素翼型為Eppler387。以笛卡爾坐標系的z軸為葉素積疊線,沿展向分布10個葉素,不同展長處葉素的弦長中點布置在z軸上,葉素弦長分布和扭轉角分布見文獻[11],最終形成的無后掠槳葉見圖1。

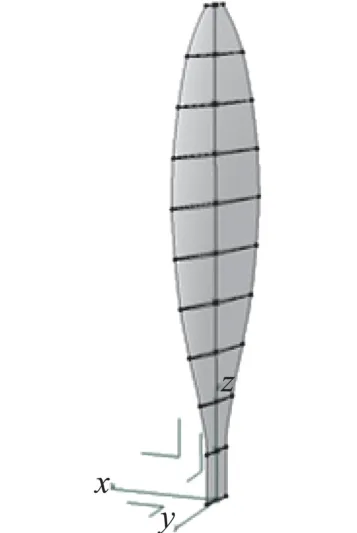
圖1 無后掠槳葉示意圖Fig.1 Unswept-blade model

后掠槳葉在無后掠槳葉的基礎上進行改動,見圖2:首先將無后掠槳葉各個葉素的弦線前后延長形成和槳葉扭轉角一致的扭轉面,其次在無后掠槳葉積疊線的一半處將積疊線分成上下兩部分,上半部分積疊線沿著y方向后掠β角度,并延長上半部分積疊線使得后掠后的頂點z坐標和無后掠槳葉積疊線頂點z坐標相同,形成后掠積疊折線,再將后掠積疊折現繞z軸旋轉任意角度使得旋轉面和扭轉面相交,然后通過相交線的頂點、無后掠積疊線中點和起點形成一條樣條曲線,將此樣條曲線投影到扭轉面上即形成后掠積疊曲線,最后按照無后掠槳葉的弦長分布和扭轉角分布在后掠積疊曲線上平均分布10個葉素形成后掠角為β的后掠槳葉。為保證后掠槳葉和無后掠槳葉的表面積近似相等,建模時近似認為槳葉在扭轉面上的投影相等則槳葉表面積相等。無后掠槳葉和后掠槳葉在扭轉平面上的投影可近似看成梯形,梯形的上底和下底相同(半展長處和槳尖處葉素弦長相同),要保證梯形面積不變,則要求梯形的高相同,因此要求后掠槳葉積疊線頂點z坐標和無后掠槳葉積疊線頂點z坐標相同。最終形成的無后掠槳葉表面積為1.47 m2,最大后掠50°時槳葉表面積1.491 m2,誤差為1.42%,在可接受的范圍。

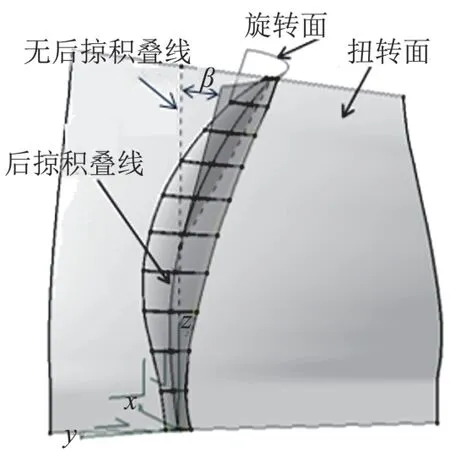
圖2 后掠槳葉建模示意圖Fig.2 Swept-blade model

1.2 螺旋槳半徑及轉速確定方法說明

半徑是螺旋槳設計的重要參數,直接影響到螺旋槳轉速的確定。無后掠槳葉的半徑為葉素積疊線的長度,后掠槳葉的半徑為后掠積疊線起點和頂點所連空間線段在垂直于平飛方向的平面上的投影,因為無后掠槳葉的積疊線起點和終點所連空間線段在垂直于平飛方向的平面上的投影就是積疊線本身,可見無后掠槳葉是后掠槳葉的特殊情況。為避免螺旋槳槳尖激波阻力的影響,本文要求所有后掠槳葉在相同的前飛速度時槳尖馬赫數相等,即所有槳葉的槳尖切向速度(2πNsR,Ns表示螺旋槳轉速,R為螺旋槳半徑)相同,因此根據無后掠槳葉螺旋槳的半徑(2.3 m)和轉速(860 r/min)以及各個后掠槳葉螺旋槳的半徑即可確定后掠槳葉螺旋槳的轉速,所有后掠槳葉螺旋槳的轉速和半徑均列于表1。

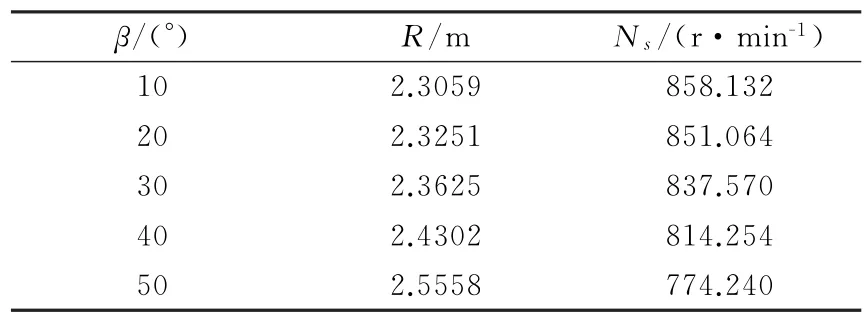
表1 后掠槳葉旋轉半徑和轉速Table 1 Rotation speed and radius of different propellers

2 數值方法與驗證

2.1 數值模擬方法與網格無關性驗證

本文所用螺旋槳的工作高度為25.9 km,此高度的大氣物理屬性如下:大氣壓強p＝2549.2 Pa,大氣密度ρ＝0.034 75 kg/m3,黏度μ＝1.46×10-5kg/(m·s),溫度T＝221.5 K,導熱系數λ＝1013 J/(kg·k)。數值模擬采用商用CFD軟件STAR-CCM＋完成,基于笛卡爾網格和周期性邊界條件僅對單個槳葉進行計算。計算域分為旋轉區(qū)域和靜止區(qū)域兩部分(圖3),考慮到槳尖空氣壓縮性影響,對槳尖區(qū)域局部加密,槳葉附近網格見圖4。采用多重參考系模型定常求解雷諾時均N-S方程和Realizable k-ε湍流模型,空間離散方法采用二階迎風插值的Roe格式。對無后掠槳葉進行網格無關性驗證,此時螺旋槳的工作狀態(tài)為:轉速Ns＝860 r/min,來流速度v0＝112.13 m/s,分別改變槳葉表面面網格尺寸為10 mm、7 mm、5 mm、3 mm,對應的體網格數量為:1075萬、1100萬、1324萬、1390萬。圖5為螺旋槳拉力T和力矩M的網格無關性曲線圖,當槳葉面網格尺寸小于5 mm(體網格1324萬)之后,計算所得拉力和力矩的波動已經很小,故對無后掠槳葉和后掠槳葉的計算均采用5 mm的槳葉面網格。

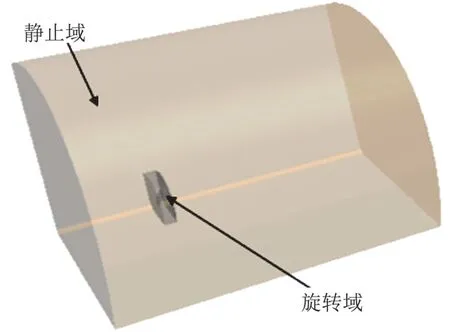
圖3 計算域示意圖Fig.3 Computational domain

圖4 槳葉附近網格Fig.4 Mesh around the blade

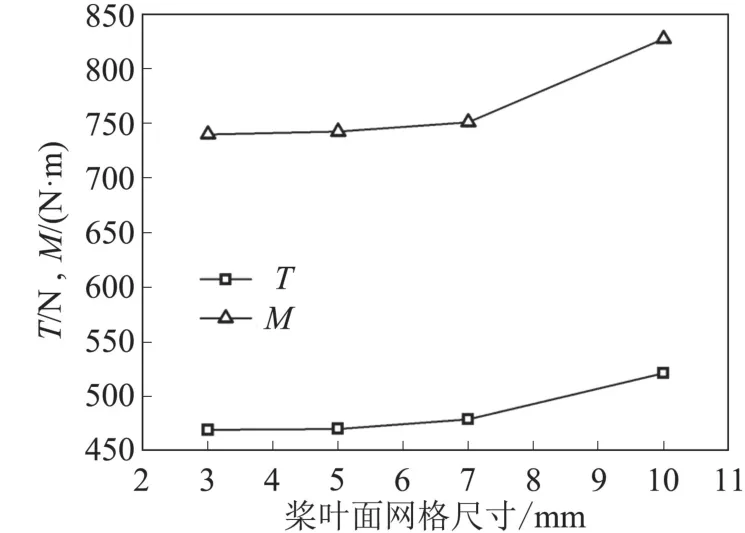
圖5 網格無關性驗證Fig.5 Mesh independency study

2.2 無后掠槳葉螺旋槳計算結果校核

工程上除采用數值模擬方法計算螺旋槳氣動性能外,也常采用片條理論計算螺旋槳氣動性能。因此采用第2節(jié)所述數值方法,計算了無后掠槳葉從設計點(進距比J＝1.7,對應的巡航速度為112.13 m/s)到進距比為2.3(巡航速度151.71 m/s)的拉力系數Ct和力矩系數Cm,在圖6中與文獻[11]中片條理論計算結果進行了對比,可見兩種方法得到的拉力系數和力矩系數隨進距比增大的變化趨勢吻合,其中數值模擬方法計算結果比片條理論計算結果略大。在文獻[30]中也有類似的結論。因此可以認為本文所用的數值模擬方法滿足當前階段的計算精度和要求,可用于初步探究后掠槳葉的氣動變化規(guī)律。

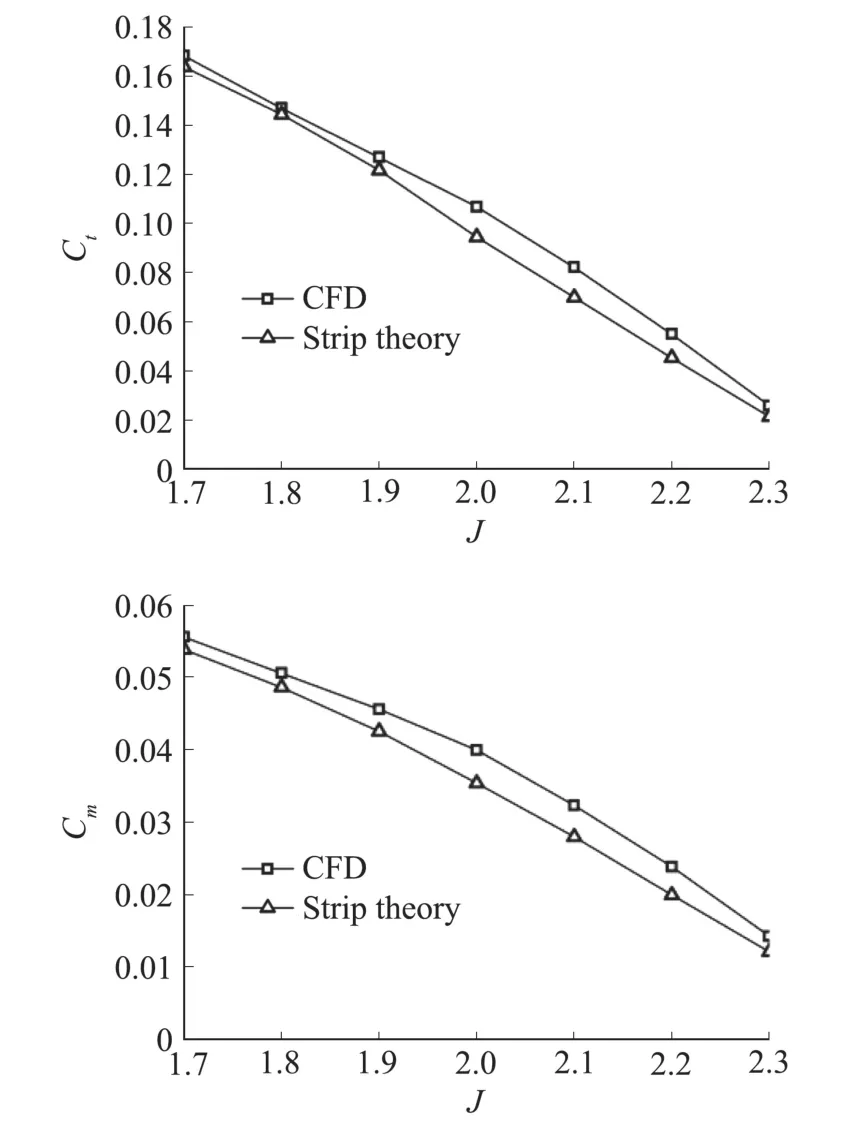
圖6 無后掠槳葉片條理論與數值計算結果對比Fig.6 Comparison between strip theory method and CFD method

3 無后掠槳葉螺旋槳氣動性能分析

圖7為進距比從1.7到2.3范圍內無后掠螺旋槳性能曲線。隨著進距比增大,拉力系數和功率系數CW均下降,效率η經過一段緩慢增加之后急劇下降。圖8為進距比在1.7、2.0、2.3時槳葉0.9倍展長處的壓力系數Cp曲線。隨著進距比的增大,翼型吸力面的負壓區(qū)范圍逐漸縮小,從前緣開始正壓區(qū)范圍逐漸擴大,而翼型的壓力面則從前緣開始負壓區(qū)逐漸擴大。圖9為進距比1.7、2.0、2.3時0.9倍槳葉展長截面的壓力云圖。可見隨著平飛速度的增大,駐點位置逐漸由下翼面轉移到上翼面。當駐點位置在上翼面時,氣流繞過前緣,速度逐漸增大,壓強隨之降低,因此進距比為2.0、2.3時,下翼面前緣附近形成負壓區(qū)。由圖9可見,平飛速度越大,駐點位置相對靠后,則氣流繞過前緣需要經過更長的路程,氣流速度更快,因此下翼面前緣區(qū)域壓強更小。而在上翼面,由于駐點位置的影響,隨著平飛速度增大,上翼面正壓區(qū)逐漸增大,從而負壓區(qū)縮小。槳葉駐點位置取決于槳葉前來流方向,槳葉前來流方向則由飛行速度和螺旋槳旋轉速度構成的速度三角形決定。由于高空長航時無人機螺旋槳多為定槳距螺旋槳,結合圖7、圖8所呈現的趨勢,根據速度三角形可知,螺旋槳轉速不變,平飛速度增大,各個葉素的迎角變小甚至會變?yōu)樨撚?導致螺旋槳拉力和功率需求降低。當平飛速度超過某一值后,螺旋槳幾乎不提供拉力,因此效率急劇下降。針對這一問題,一般采用調整螺旋槳轉速的方法來解決。但是,由圖8還可以看出,三個進距比工況下,槳尖均受到明顯的壓縮效應影響,這說明即便通過調整螺旋槳轉速和飛行速度進行匹配以避免槳葉迎角的減小,但是槳尖壓縮效應對螺旋槳氣動性能的影響始終存在,因此,如何消除槳尖壓縮效應是提高螺旋槳氣動性能的關鍵。

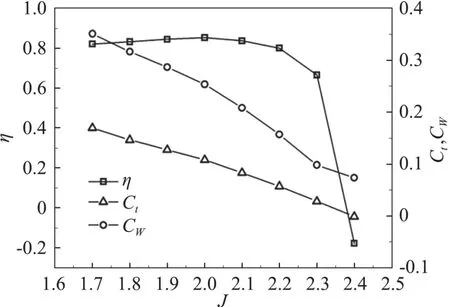
圖7 無后掠槳葉性能曲線Fig.7 Performance curve of unswept-blade propeller

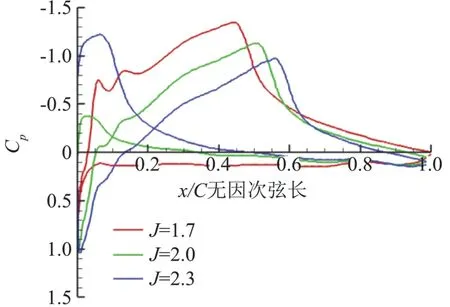
圖8 隨進距比增大壓力系數曲線圖變化對比Fig.8 Comparison of pressure coefficient curve with increasing of advance ratio

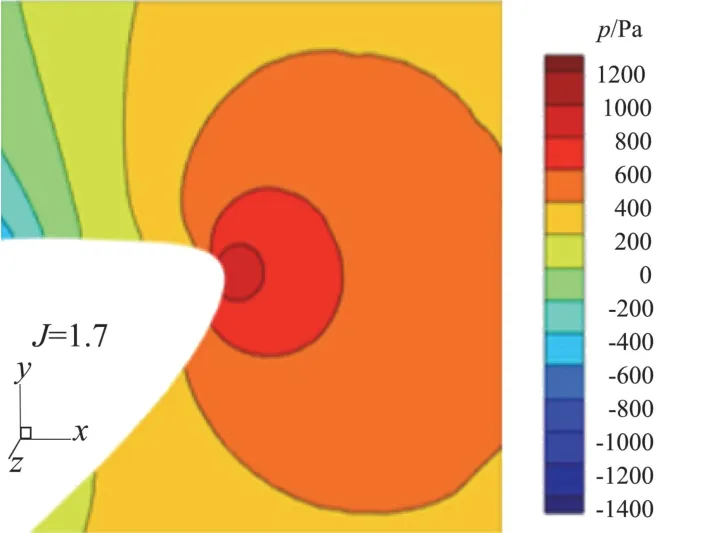
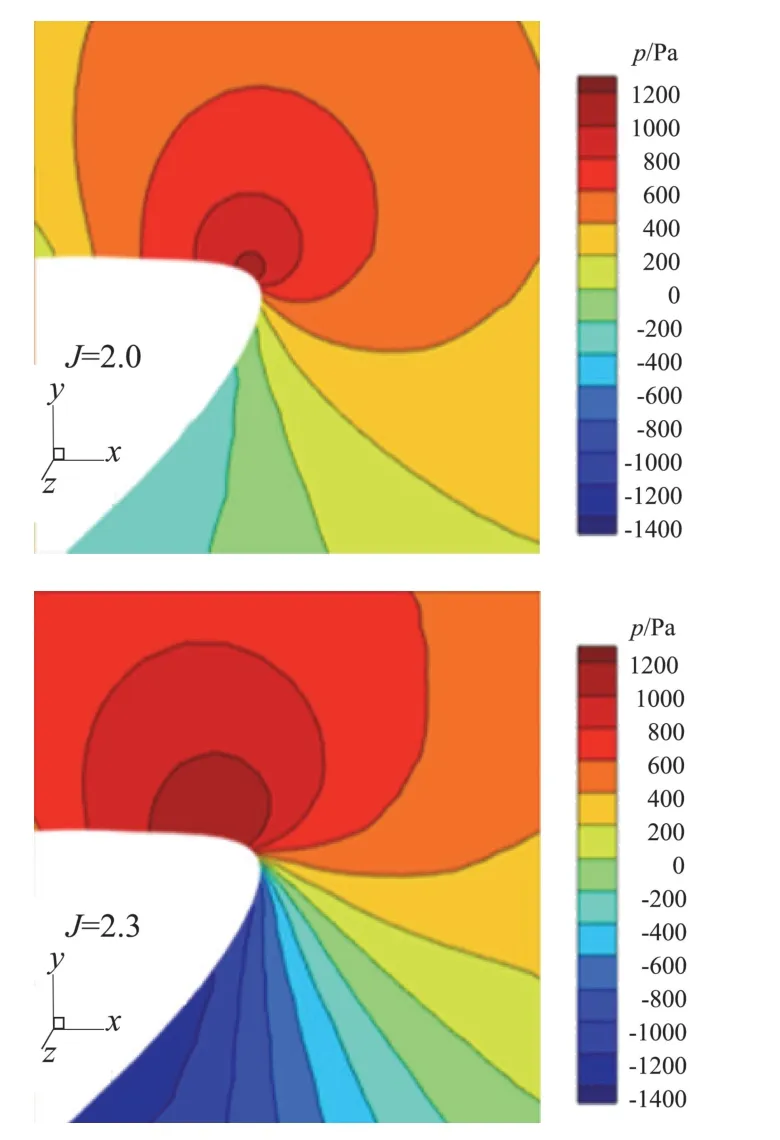
圖9 不同進距比0.9倍展長壓力云圖Fig.9 Pressure distribution at 0.9 spanwise length location with different advance ratio

4 后掠槳葉計算結果及分析

根據第1.2節(jié)提到的不同后掠槳葉要保證槳尖切向速度相同的要求,可知不同后掠螺旋槳直徑D和轉速的乘積是一定值。又根據進距比的定義式:J＝v0/(Ns·D),可知不同后掠角的螺旋槳進距比和平飛速度一一對應,因此不同后掠角的螺旋槳氣動性能可以放在同一段進距比的范圍內進行比較。這樣既可以表示各個螺旋槳自身的氣動性能又可以進行不同后掠槳葉之間的性能對比。采用與無后掠槳葉相同的計算方法分別對各個后掠槳葉進行計算,結果分析如下。

圖10~圖12分別為不同后掠角螺旋槳的拉力、功率和效率對比圖。由拉力對比曲線圖可知,在平飛速度較低時(進距比1.7、1.8),隨著槳葉后掠角的增大,拉力先增大然后降低,在此范圍內槳葉后掠角為40°時拉力最大,進距比超過1.8之后,螺旋槳拉力隨著槳葉后掠角的增大而增大,整體來看后掠槳葉螺旋槳都能提供比無后掠槳葉螺旋槳更大的拉力。由功率對比曲線可知,隨著槳葉后掠角的增大,螺旋槳的功率需求也隨之增大,且在較高平飛速度時對功率的需求更高。由效率對比曲線可知,槳葉后掠可以使螺旋槳在較高的平飛速度維持較為理想的效率,且后掠角越大,螺旋槳可在更高的平飛速度下高效工作。后掠角從10°增大到40°時,螺旋槳的峰值效率隨著后掠角的增大而增大;當槳葉后掠角達到50°時,螺旋槳的峰值效率下降,且在較低的速度范圍內,螺旋槳效率下降明顯,不利于無人機低速巡航飛行。本文的計算結果還顯示,當后掠角在30°時,螺旋槳在高速工作時的效率開始明顯提高,最佳的后掠角應該在30°和50°之間,此時,螺旋槳在較低速度范圍內效率變化不大,在較高速度范圍內能夠明顯提高螺旋槳效率,有效加寬螺旋槳的工作范圍。

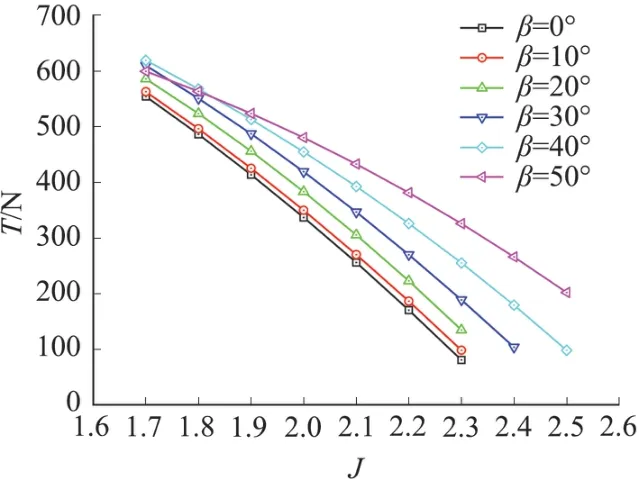
圖10 不同后掠角螺旋槳拉力對比Fig.10 Thrust comparison for different sweep angles

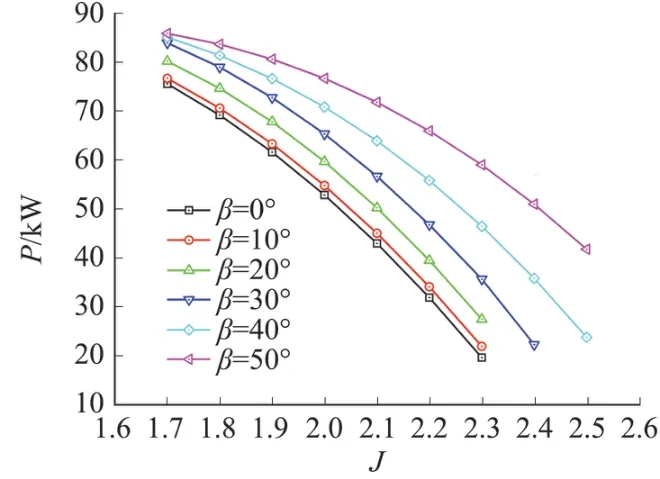
圖11 不同后掠角螺旋槳功率對比Fig.11 Power comparison for different sweep angles

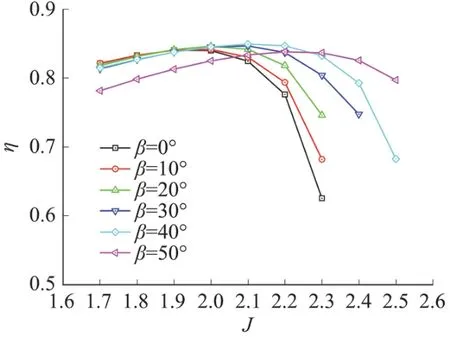
圖12 不同后掠角螺旋槳效率對比Fig.12 Efficient comparison for different sweep angles

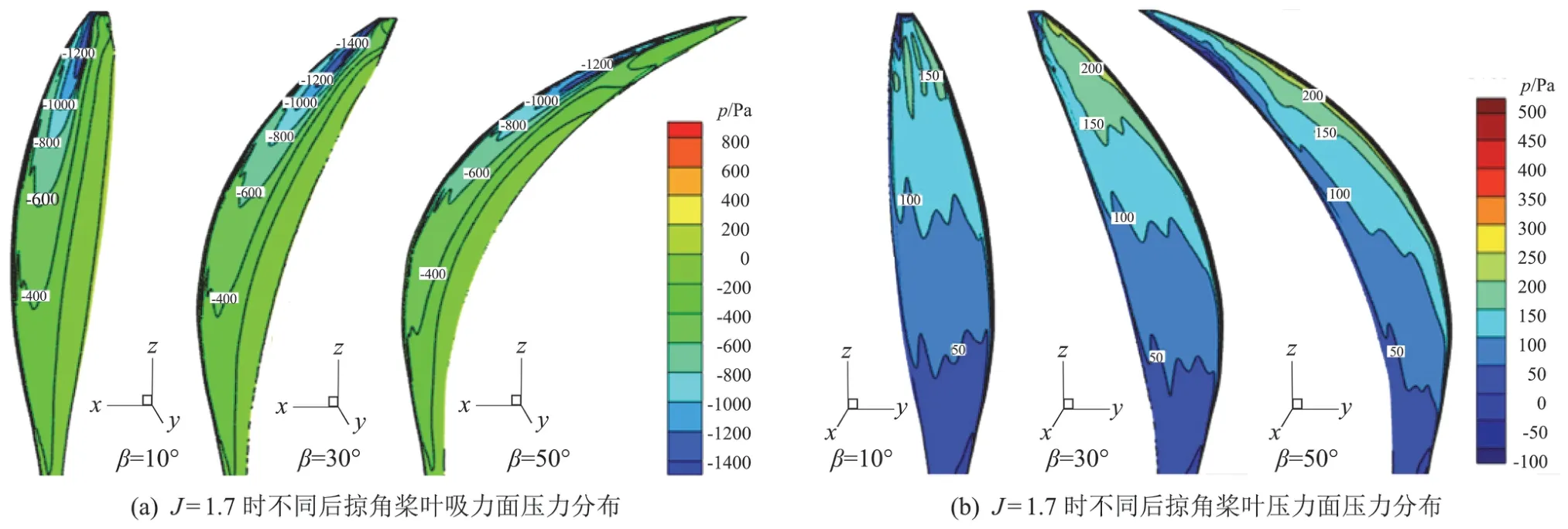
圖13 J＝1.7時不同后掠角槳葉壓力分布對比Fig.13 Comparison of pressure distribution on blade for different sweep angles at J＝1.7

現分析J＝1.7時,后掠角分別為10°、30°、50°槳葉吸力面和壓力面的壓力云圖(圖13),探究槳葉上壓力分布隨后掠角的變化規(guī)律。從圖13(a)吸力面的壓力值來看,隨著后掠角的增大,負壓值先增大后降低。從壓力分布來看,當后掠角為10°、30°時,最大負壓區(qū)都在槳尖處;當后掠角為50°時,最大負壓區(qū)由槳尖向槳葉中部移動。從圖13(b)壓力面的壓力云圖來看,后掠角為10°、30°時,壓力面的最大正壓區(qū)在槳尖處,從槳尖到槳根壓強逐漸減小;后掠角為50°時,壓力面的最大正壓區(qū)從槳尖下移到槳葉中上部。

圖14為進距比1.7時、不同后掠角槳葉0.7倍展向截面的前緣壓力云圖。從圖中可以看出后掠會導致駐點位置下移。圖15為后掠槳葉葉素分布位置(紅色方點)和無后掠槳葉葉素分布位置(藍色點)對比,可以看出在各個展向位置,后掠槳葉的迎角都大于無后掠槳葉。正是因為后掠使得槳葉的平均迎角增大,后掠槳葉的功率需求更大,這一點也可以從圖11功率對比圖中得出。因為后掠會使得槳葉平均迎角變大,且隨著后掠角增大,這種趨勢更加明顯,所以在圖13(b)中后掠角為30°、50°時最大正壓區(qū)域比后掠角為10°時大,而后掠角為50°時由于槳尖三維效應的緣故,在槳尖處的最大正壓區(qū)域消失。同樣由于迎角增大的原因,在圖13(a)中,后掠角30°時的最大負壓高于后掠角10°時的最大負壓,但是后掠角為50°時由于三維效應的緣故最大負壓值又低于后掠角為30°的槳葉,因此在三維效應和迎角增大的共同影響下,使得三種槳葉中,后掠30°的槳葉能提供最大的拉力。

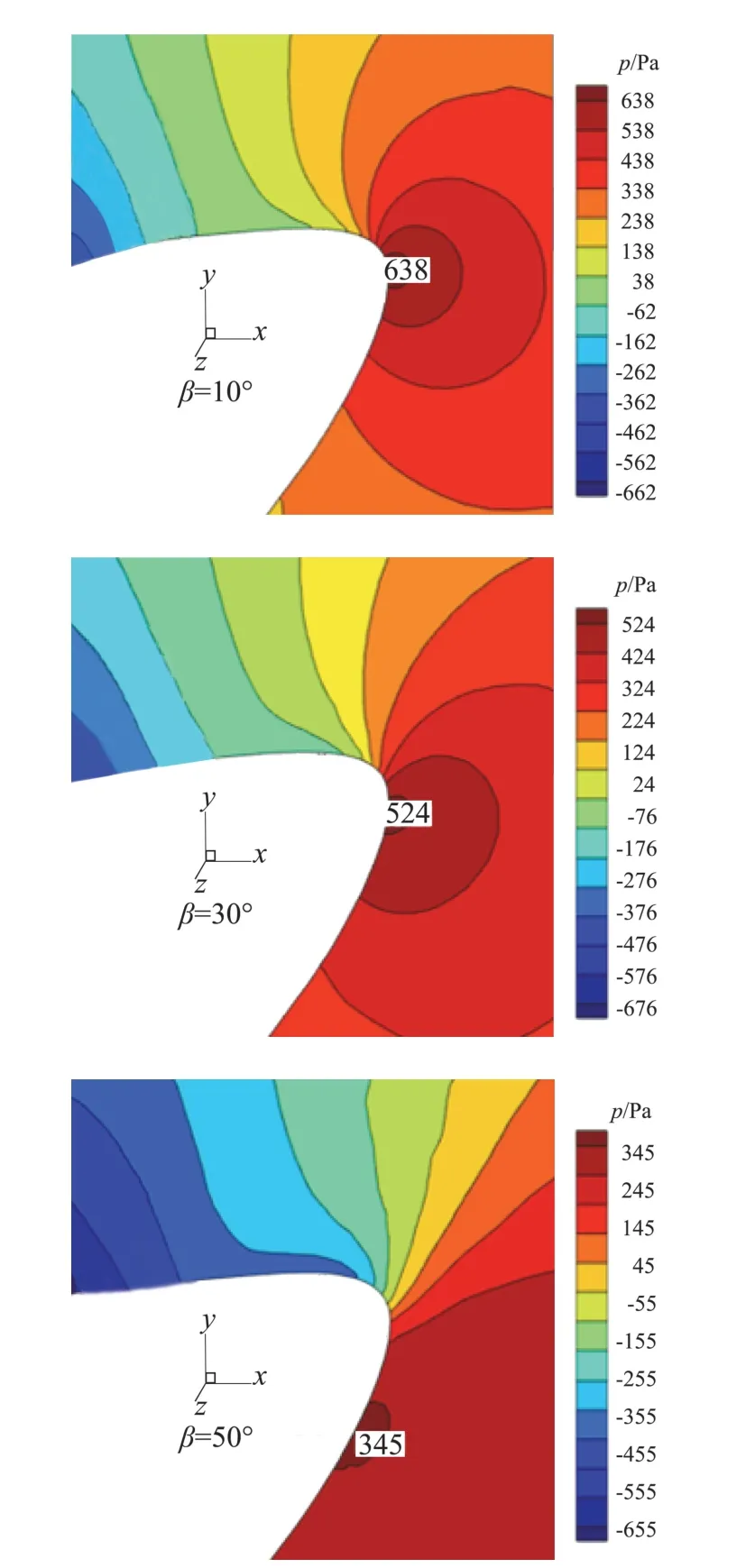
圖14 不同后掠角前緣駐點c位置對比Fig.14 Comparison of leading edge stagnation point location for different sweep angles

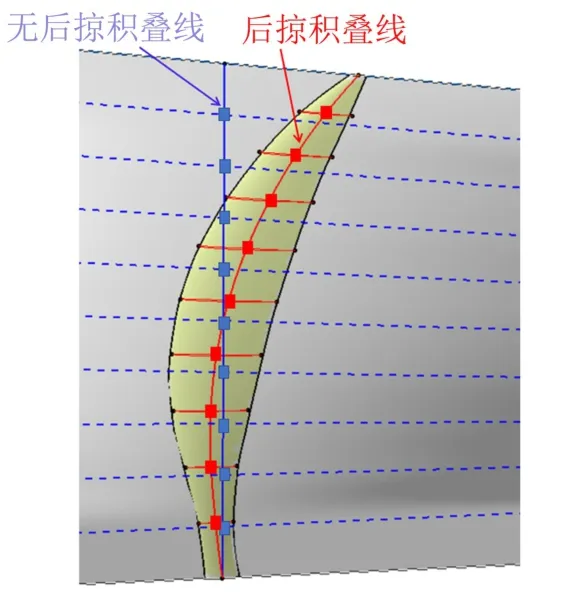
圖15 后掠和無后掠槳葉葉素分布位置對比Fig.15 Comparison of blade elements position of swept and unswept blade

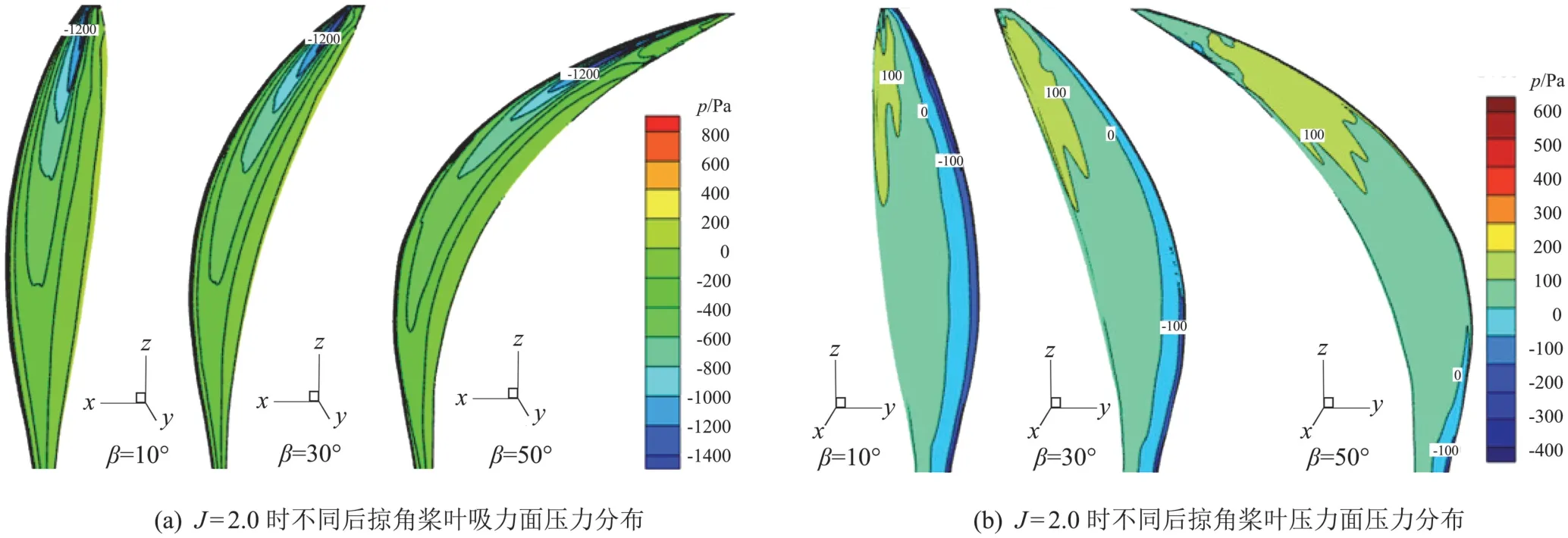
圖16 J＝2.0時不同后掠角槳葉壓力分布對比Fig.16 Comparison of pressure distribution on blade for different sweep angles at J＝2.0

圖16為進距比2.0時,后掠角分別為10°、30°、50°時槳葉吸力面和壓力面的壓力云圖。吸力面的壓力變化情況和進距比為1.7時有相同之處也有所區(qū)別:后掠角為10°、30°時最大負壓區(qū)在槳尖處,后掠角為50°時同樣由于槳尖三維效應的緣故,使得最大負壓區(qū)向槳葉中部移動。壓力面和吸力面的壓力值變化情況與進距比為1.7時有所不同,由圖9可知進距比為2.0時,槳葉處在負迎角的工作狀態(tài),因此在壓力面能夠看到明顯的負壓區(qū)域,因為后掠使得槳葉的迎角變大,從而在進距比2.0時,后掠50°的槳葉迎角大于后掠10°、30°的槳葉,即后掠50°的槳葉更接近于正迎角的工作狀態(tài),氣流從上翼面繞過前緣到達下翼面的過程中,壓降不及后掠角為10°、30°時劇烈,因此在圖16(b)中可以看到,后掠角為50°時,在壓力面前緣附近形成的負壓區(qū)域小于另外兩種情況,從吸力面壓力分布可見,三個槳葉的最大負壓值相同,這是由于迎角為負及迎角隨后掠角的變化導致,后掠50°時更接近正迎角,因此氣流在前緣處可以更加充分的加速,使得其最大負壓值能夠相等于其余兩個后掠槳葉。這正是圖10中當進距比在1.9之后,后掠角為50°的槳葉所產生的拉力最大的原因。

圖17為進距比1.7時,后掠角分別為0°、30°時0.95倍展長處切面的壓力云圖,由圖可見在槳尖處有明顯的壓縮效應,后掠角0°時,槳尖處形成了激波,激波后與激波前絕對靜壓比為1.45,當后掠角為30°時,激波減弱,波后、波前絕對靜壓比為1.41,可見槳葉后掠可以減弱槳尖激波強度,這也是后掠槳葉比無后掠槳葉能夠提供更大拉力的原因。由于本文所用螺旋槳工作高度較高,大氣密度低導致雷諾數較低,附面層較厚,氣流在上翼面易發(fā)生分離,由圖可見在上翼面存在激波-附面層干擾現象,并且后掠角越大激波-附面層干擾現象越明顯,這是因為后掠會使得槳尖附面層變厚,本文認為激波-附面層干擾一定程度上減弱了槳葉上表面的激波強度,這可以從圖17壓力云圖及圖18壓力系數曲線對比圖中看出。由壓力系數曲線對比(圖18)可見,由于后掠角30°時的當地迎角大于后掠角0°時的當地迎角,因此在激波前,后掠角30°時吸力更大,在激波之后,一方面由于后掠減弱了激波強度,另一方面由于激波-附面層干擾的作用使得后掠角30°時的吸力更大。

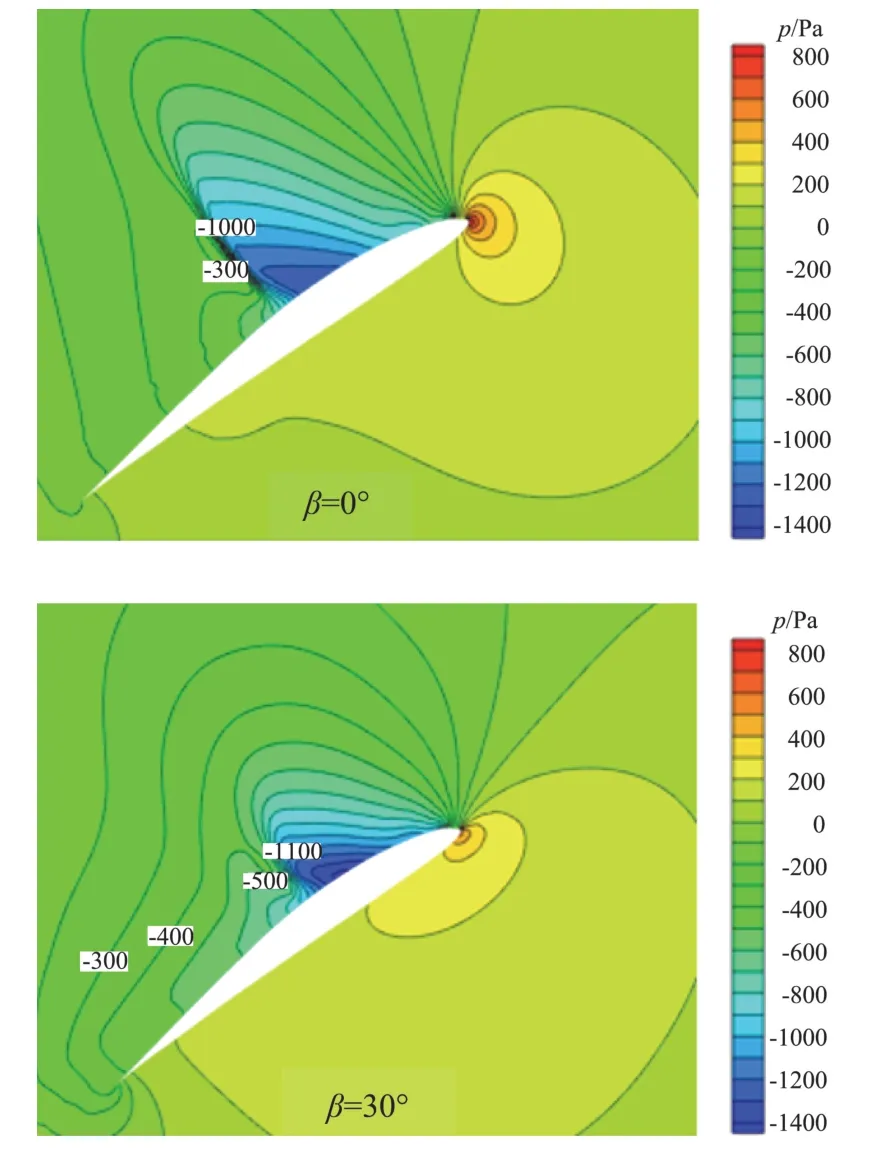
圖17 J＝1.7時后掠與不后掠槳葉槳尖激波比較Fig.17 Comparison ofshock wave at blade tip between swept and unswept blade

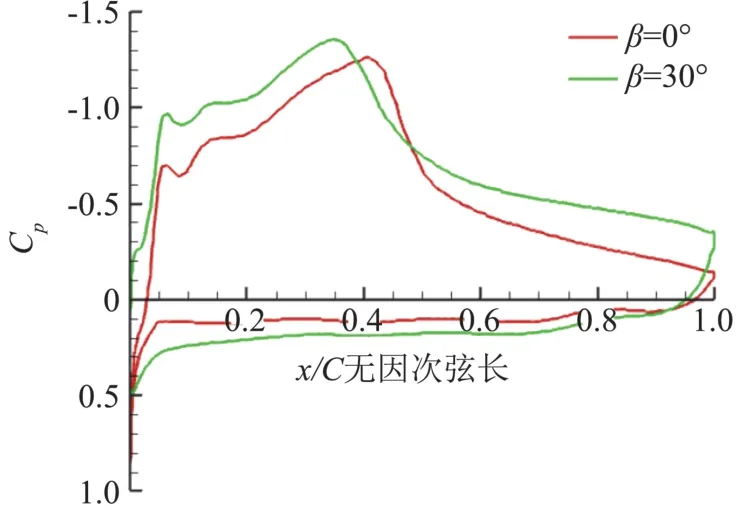
圖18 J＝1.7時后掠與不后掠槳葉槳尖壓力系數比較Fig.18 Comparison of pressure coefficient at blade tip between sweptand unswept blade

5 結 論

本文將槳葉后掠的設計思想應用于高空長航時無人機螺旋槳槳葉設計上,在無后掠槳葉的基礎上,分別設計了五個后掠槳葉,應用數值計算方法,分析了高空長航時無人機螺旋槳在高速工況時效率下降的原因,對比了不同后掠角螺旋槳拉力、功率和效率的變化趨勢,分析了后掠對槳葉氣動性能影響的原因,得出如下結論:

提高螺旋槳高速性能的關鍵在于減弱槳尖壓縮效應,后掠槳葉能夠達到這一目的,但是后掠槳葉的氣動性能受迎角變化、槳尖三維效應、槳尖激波強度、激波-附面層干擾綜合影響。當槳葉后掠角在30°和50°之間時,可使螺旋槳能夠在原設計點之后加寬螺旋槳的高效工作范圍,提高高空長航時無人機的高速性能,滿足無人機快速爬升和快速機動的設計要求。