基于動理學模型的多尺度隨機粒子方法

費 飛,張 俊,柳朝暉

(1.華中科技大學 航空航天學院,武漢 430074;2.北京航空航天大學 航空科學與工程學院,北京 100191;3.華中科技大學 能源與動力工程學院 煤燃燒國家重點實驗室,武漢 430074)

0 引 言

跨流域流動廣泛存在于航空航天工程問題中,如航天器微噴管中的流動[1-2]和航天飛行器的再入過程[3]。流動的跨流域特性可以由克努森數(Kn)表述,其為分子平均自由程和流動特征尺度的比值,因此分子平均自由程和流動特征尺度的變化均會使流動呈現多尺度的特點。前者如,在高空真空環境下,噴管中的流動由連續流過渡到自由分子流;而在海拔100~50 km飛行的再入飛行器,由于鈍頭體背風面氣流急劇膨脹產生低壓低密度區,其流動也具有稀薄/連續流共存的跨流域特點。后者如,在臨近空間飛行器的前緣、表面微結構以及激波附近[4],特征尺度小于平均自由程,流動在局部是非平衡的,這一多尺度的流動特性顯著影響著臨近空間飛行器的氣動力、熱[5-6]。除航空航天工程以外,在微納尺度的機電器件(MEMS)中,由于微納器件特征尺度的變化,跨流域流動問題同樣廣泛存在,如微納器件壁面附近的流動和催化反應往往也都具有典型的多尺度非平衡流動[7]特點。

當流動的特征尺度相當于氣體分子平均自由程量級時,流動處于稀薄流區域,此時分子的間斷效應變得顯著,Navier-Stokes(N-S)方程的連續性假設失效,因此基于N-S方程的CFD方法無法模擬包含稀薄氣體效應的跨流域流動。發展CFD和稀薄氣體求解格式的混合方法是一種有效的解決途徑[8-10]。但由于兩種格式基于不同形式和尺度的控制方程,它們的耦合界面處會遇到數值和物理的困難[11]。其一,是耦合界面位置的選取,物理上要求兩種方法的分界面位于近平衡態區域。其二,是微觀和宏觀計算信息在耦合界面處的傳遞。特別當稀薄氣體求解格式選取隨機粒子方法時(如DSMC方法),還需要額外處理粒子方法統計噪聲的影響。這些問題在混合算法的發展過程中雖已有改善,但對算法實現仍然提出了較高要求。

如直接從介觀統計物理出發,各尺度的氣體流動均滿足基于氣體分子幾率密度分布函數的Boltzmann方程。相比于N-S方程,Boltzmann方程對氣體流動適用范圍更寬泛,從形式上看,其與N-S方程有兩點差別:

其一,該方程不僅描述了流場的時空分布,還包含了氣體分子速度在速度空間的分布。因此,對高維速度分布函數(VDF)的求解使動理學方法的計算量遠大于傳統的CFD格式[12]。具體來說,速度分布函數可以在速度空間中直接離散,通過速度離散坐標點確定性的表示;也可以對速度空間隨機采樣,通過隨機的模擬粒子概率性的表示。前者如離散速度法[13]、Boltzmann方程譜方法[14-15]、離散Galerkin方法[16]、有限差分法[17]等,后者如蒙特卡洛直接模擬方法(DSMC)[18]。相比概率性的隨機粒子模擬方法,確定性方法,沒有統計漲落,因此對低速的非平衡流動,以及非定常問題具有很好的適用性。但對于高速流動,隨著速度相空間增大,確定性方法需要的計算內存急劇增加,需要發展速度空間自適應[19]、無存儲[20]、大規模并行計算[21-22]等技術提高計算效率。相反,對概率性的隨機粒子方法,隨著流動速度增加,統計漲落的影響逐漸減小,計算效率將大大提高。特別的,在包含化學反應、氣體離解等復雜物理化學過程的高超聲速稀薄氣體流動模擬中,以DSMC為代表的隨機粒子方法具有顯著優勢。

其二,Boltzmann方程中除了流動特征尺度外,還包括分子碰撞尺度(如分子平均自由程和平均碰撞時間),氣體分子所具有的碰撞松弛演化特性決定了Boltzmann方程碰撞項的剛性較強。因此,對確定性方法,Boltzmann方程顯式離散求解的時間步長受到格式穩定性條件的限制,例如對于大尺度非規則尖前緣飛行器繞流,由物形的非規則性網格確定的格式穩定條件時間步長甚至小于氣體分子平均碰撞時間[23-24];而對概率性的隨機粒子模擬方法,雖然不存在穩定性問題,但由于計算中將分子運動和碰撞解耦求解,當時間步長大于分子平均碰撞時間時,將會引入較大的數值黏性。對Kn數遠小于1的連續流動而言,時空步長的限制使直接模擬Boltzmann方程的計算量變得非常巨大。因此,Boltzmann方程計算格式雖然理論上可以模擬多尺度流動,但實際求解跨流域流動時的效率是極低的。

提高Boltzmann方程動理學格式對高超聲速復雜飛行器跨流域流動的計算效率有兩個主要途徑:

一是從碰撞項的物理模型出發,利用Boltzmann模型方程近似處理碰撞項,減小碰撞項的計算量,因為碰撞項是連續流動計算中占比最大的部分。如采用BGK和Fokker-Planck方程:

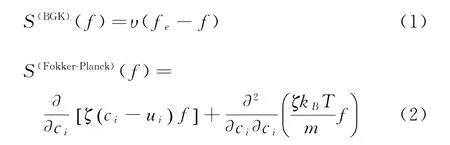
其中:f和fe分別是氣體的速度分布函數和平衡態分布,ci和ui分別是氣體分子運動速度和宏觀流動速度,T為溫度,m為分子質量,kB為玻爾茲曼常數,υ和ζ分別是BGK和Fokker-Planck模型的松弛系數。上述兩類Boltzmann模型方程利用速度分布函數的碰撞松弛演化特性來近似碰撞過程,對概率性粒子方法,近年來發展了一系列基于Fokker-Planck[25]或者BGK模型[26]的隨機粒子方法,并在高速氣體流動以及多組分流場的模擬中得到了成功的應用。

二是從碰撞項的求解格式出發,減少Boltzmann方程中碰撞松弛演化特性對數值上時空離散的限制,發展多尺度的動理學方程計算格式[27-28]。如基于隨機粒子的多尺度Fokker-Planck[29]、BGK[30]和DSMC[31]方法,和基于離散速度坐標法,對Boltzmann模型方程分別在位置空間、速度空間離散數值求解的GKUA[21-22,32-33]及利用上述方法離散速度坐標法與BGK型有限體積格式相耦合發展的統一格式UGKS[34-35]、DUGKS[36]等。

本文將從對隨機粒子方法模擬得到的氣體輸運系數離散誤差的分析出發,分別介紹基于BGK和Fokker-Planck模型的兩類多尺度隨機粒子方法。區別于傳統的BGK和Fokker-Planck隨機粒子方法,多尺度隨機粒子方法不僅在分子自由運動主導的稀薄流域,能夠模擬分子的間斷碰撞效應,反應流動的非平衡現象;在碰撞主導的連續流域,也能夠通過在分子運動中耦合連續碰撞作用,反應物理上正確的分布函數演化,滿足宏觀流體力學方程的輸運性質。如Chen等在文獻[37]中分析,無論從Kn數還是Ma數的角度,N-S方程主導的黏性流區域在跨流域流動中都是不可忽視的。因此,連續區滿足N-S方程的宏觀輸運性質,可以使氣體動理論方法在物理上滿足模擬跨流域流動的要求。最后,我們將給出幾種隨機粒子方法的數值比較分析。

1 隨機粒子方法模擬得到的輸運系數離散誤差

1.1 DSMC方法

澳大利亞科學家Bird在20世紀60年代提出的直接模擬Monte Carlo(DSMC)方法是目前解決稀薄氣體流動最有力的數值計算工具。DSMC方法采用拉格朗日方法跟蹤模擬分子,首先在網格中選取分子碰撞對,其次將分子運動和碰撞解耦處理,其模擬得到的輸運系數與網格大小和時間步長有關。利用統計物理的Green-Kubo理論[38],Garcia和Hadjiconstantinou等[39-40]分析了DSMC方法的時空離散誤差(Green-Kubo理論將流體的輸運系數與平衡態下的時空漲落關聯在一起,因此可以分析隨機粒子方法模擬得到的氣體輸運系數的時空離散誤差)。以黏性系數為例,當Δ/λ和Δt/τc在1附近,DSMC方法硬球模型的數值黏性與網格大小和時間步長的依賴關系分別為:

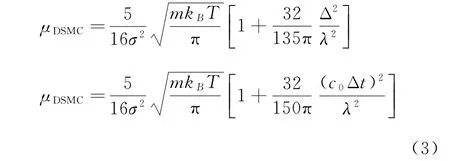
其與時間步長和網格大小的平方成正比。式(3)中,σ為碰撞截面,λ和τc分別為平均自由程和平均碰撞時間,Δ和Δt分別為網格大小和時間步長。當DSMC方法的時間步長和網格大小分別和分子平均碰撞時間和平均自由程相當時,數值黏性的相對誤差Δμ/μ分別約為5%和10%。因此,為了保證流動物理上的正確性,這就要求DSMC方法的時間步長要比分子平均碰撞時間小,選取碰撞對的距離也要小于分子平均自由程。

1.2 BGK模型隨機粒子方法

BGK模型的氣體輸運系數可以根據Chapman-Enskog展開得到[41],同樣以黏性系數為例,BGK模型的氣體黏性系數為:

其中p為壓強。不同于DSMC方法直接求解氣體分子的雙體碰撞,BGK模型通過分布函數的碰撞松弛演化特性來近似表征Boltzmann方程碰撞項(方程(1)),因此BGK模型方法得到的氣體輸運系數的空間離散誤差小于DSMC方法。但在傳統的BGK模型的數值求解中,因BGK模型將其碰撞頻率視為常數進行完全積分,假設首先自由對流Δt?τc的時間,然后以常數碰撞頻率松弛至當地平衡態,則BGK模型方法得到的氣體黏性正比于時間步長:

1.3 Fokker-Planck模型隨機粒子方法

Fokker-Planck模型也是采用松弛過程近似Boltzmann方程中的碰撞項。與BGK模型不同的是,Fokker-Planck模型中的松弛過程針對氣體分子的速度,而BGK模型針對的是速度分布函數整體。因此物理上,Fokker-Planck方程等價于單個分子運動的Uhlenbeck-Ornstein隨機過程[42],分子速度和位移由Langevin方程表征:

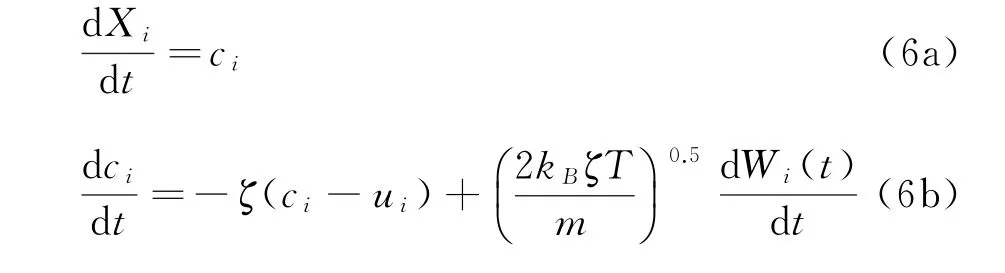
其中,ci和Xi分別代表分子速度和位置,Wi(t)代表Wiener過程。Fokker-Planck模型的氣體輸運系數同樣可以根據Chapman-Enskog展開求取[43],如黏性系數為:

Jenny等基于Langevin方程(6)構造了Fokker-Planck模型的積分格式(FPM)[25]。Langevin方程的演化包含了隨機粒子當地的宏觀平均速度和溫度,和其它隨機粒子方法一樣,FPM方法中假設模擬分子的宏觀平均速度和溫度為當前時刻值,并顯式求解分子運動過程。因此,當Δt＞τc時,Fokker-Planck模型積分格式得到的氣體黏性將會偏離方程(7)的理論值。通過分析Fokker-Planck方程動量和能量矩方程的積分形式,并利用Green-Kubo理論,可以給出FPM方法得到的氣體輸運系數與時間離散尺度的解析表達式[29],以黏性為例:

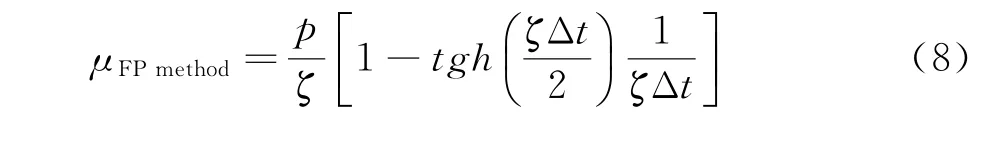
綜上,圖1給出了DSMC、BGK、FPM三種隨機粒子方法得到的氣體流動數值黏性(Δμ＝μBGK/FPmethod－μ0,μ0為動理學方程的物理黏性)隨時間步長變化的曲線。三種方法對應時間步長得到的氣體黏性系數分別通過Couette流動計算得到。可以看出,當Δt/τc?1時,DSMC和BGK方法得到的氣體數值黏性與Δt的一次方成正比;在Δt/τc＝1附近時,DSMC的結果與Δt的二次方成正比;數值結果與方程(3)和方程(5)的理論預測一致。FPM方法得到的氣體數值黏性與時間步長的依賴關系稍復雜,在大時間步長時收斂至2μ0,從圖1可以看出我們給出的解析結果(8)與數值實驗相符合。

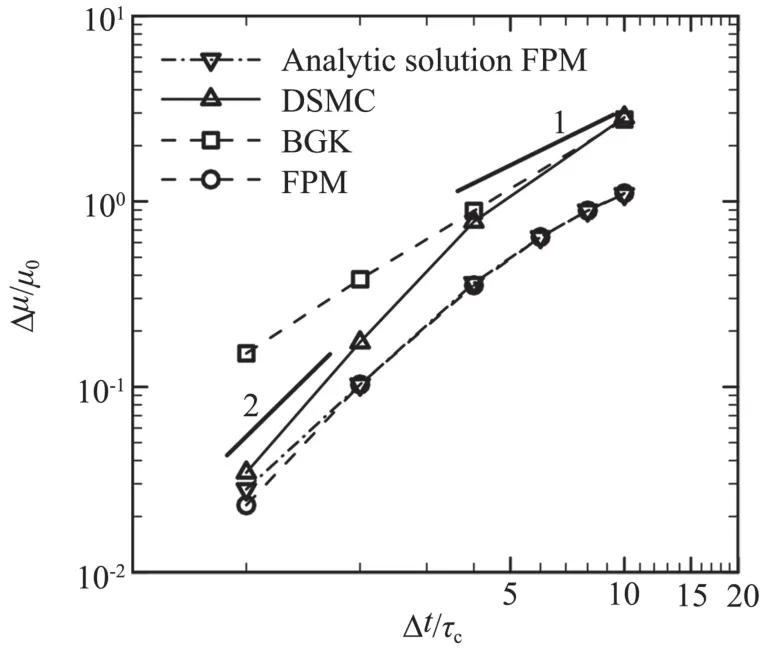
圖1 DSMC、BGK、FPM方法黏性系數與時間步長的關系Fig.1 Relation of the viscosity and time step for the DSMC,BGK and FPM method

2 多尺度隨機粒子方法

從上節隨機粒子方法模擬得到的氣體輸運系數的時空離散誤差的分析可以看出,DSMC、Fokker-Planck或BGK模型隨機粒子方法的黏性系數與時間步長相關,對連續流動,隨著時間步長的增加這些計算方法并不滿足N-S方程的輸運性質。造成較大時間離散尺度下數值黏性的主要原因是,這些隨機粒子方法求解中將分子運動和碰撞解耦處理。因此,隨著時間步長的增加,速度分布函數的演化過程存在顯著誤差,流場中的動量和能量輸運被大大高估了。在小Re數或中等Kn數的區域,跨流域流動中黏性和熱傳導的作用較為重要,直接采用傳統的隨機粒子方法顯然無法得到與物理流動一致的結果。為了克服隨機粒子方法這一困難,我們將分別介紹基于FPM和BGK方法發展的兩種適用與跨流域流動計算的多尺度隨機粒子方法。

2.1 多尺度Fokker-Planck模型隨機粒子方法

對連續流,為了構造大時間步長下仍滿足N-S方程輸運性質的隨機粒子方法,需要將分子運動和碰撞過程耦合計算[37]。在Fokker-Planck模型方法中,這一要求可以通過聯合求解Langevin方程(6)實現,解析得到Δt時間后分子速度和位移的聯合分布函數為:

則Δt時間步長后分子的速度和位移,通過取樣聯合分布函數(9)得到,這即是FPM積分格式的核心思想。當Δt/τc?1時,根據方程(9)和式(10),分子的速度分布滿足平衡態,而其位移分布滿足分子的擴散,滿足N-S方程的輸運特性。但由方程(8)可知,FPM方法模擬得到的氣體輸運系數在Δt/τc?1和Δt/τc?1兩個條件下是不一致的。以黏性系數為例,根據方程(8),兩個時間尺度極限下的黏性系數分別為p/(2ζ)和p/ζ。如將Langevin方程(6)中的阻力系數選為恒定值ζ＝p/(2μ),正如傳統FPM方法的做法,對較大的時間步長是不合適的。因此,多尺度Fokker-Planck模型隨機粒子方法(Particle Fokker-Planck Algorithm with Multiscale Temporal Discretization,MTD-FPM)在FPM積分格式基礎上,根據其黏性系數與時間步長的表達式(8),選取阻力系數為時間步長的函數ζ(μ,Δt),從而保證對任意的時間步長,隨機粒子方法模擬得到的氣體輸運系數與模型方程的物理值保持一致。類似FPM方法,對等溫流動,MTD-FPM方法的主要步驟如下:

(1)模擬分子速度和位置的初始化;

(2)根據流場宏觀量及式(8),計算阻力系數ζ(μ,Δt);

(3)根據聯合分布函數(9)取樣模擬分子Δt時間后分子速度和位移;

(4)計算補償壓力項對模擬分子速度的貢獻,并更新分子速度;

(5)統計流場宏觀量。如未計算結束,從步驟2繼續下個時間步循環。

步驟(4)中MTD-FPM方法額外的壓力項修正是因為在FPM積分格式中,壓力項也是時間步長的函數:

當Δt/τc?1,pFPM→0。假設壓力修正項對計算網格內的每個模擬粒子都是相同的,那么,模擬粒子的速度在步驟4后更新為:

其中壓力梯度?p/?xi由宏觀方程差分計算得到。對于非等溫流動,MTD-FPM方法的計算步驟也是相似的,具體介紹可以參考文獻[29]。

2.2 多尺度BGK模型隨機粒子方法

和Fokker-Planck模型類似,另一常見的模型方程——BGK模型為:

其中碰撞項J＝υ(fe－f)。BGK模型的普朗特數為1,為了得到正確的普朗特數,在計算中一般采用修正后的BGK模型,如Shakhov(SBGK)模型和Ellipsoidal Statistical BGK(ESBGK)模型。ESBGK模型由Holway[44]和Cercignani[45]提出,并滿足H定理[46]。本文將重點討論基于ESBGK模型的多尺度隨機粒子方法。

ESBGK模型的碰撞項可寫為:

其中υES＝Pr·υ,fG為各向異性的Gaussian分布函數:

R＝kB/m,σij為剪切應力。ESBGK模型的隨機粒子方法(SP-ESBGK)由Gallis、Torczynski[47]發 展。SP-ESBGK方法同樣將分子對流運動和碰撞解耦處理,由方程(13),SP-ESBGK方法分子對流運動和碰撞松弛步的控制方程可以分別寫為,

對流運動:

SP-ESBGK方法的算法實現與DSMC方法類似,唯一區別是碰撞項的處理。根據方程(17b),模擬分子自由運動一個時間步長后,網格中Ns＝int{ Nc[ 1－exp(－υESΔt)]}個粒子被隨機選中并重新根據Gaussian分布函數(15)取樣分子速度;剩余的模擬分子速度保持不變。Nc為網格中的模擬分子個數,“int”為取整操作。因為無需取樣雙體碰撞,所以對連續流動,SP-ESBGK方法的效率遠高于DSMC方法,其主要實現步驟可總結為:

(1)模擬分子速度和位置的初始化;

(2)模擬分子位置更新,分子對流,式17(a);

(3)模擬分子速度更新,分子碰撞,式17(b);

(4)統計流場宏觀量。如未計算結束,從步驟2繼續下個時間步循環。

雖然SP-ESBGK方法通過采用近似的碰撞項,提高了對連續流的計算效率,但由于分子運動和碰撞的解耦處理,隨著時間步長增加,其時間離散誤差將使模擬得到的輸運系數遠大于物理值(見圖1),因此對黏性和熱傳導不可忽略的流動區域是不準確的。為了減小時間離散誤差,構造滿足N-S方程輸運性質的ESBGK模型隨機粒子方法,我們在原對流運動和碰撞松弛步中分別考慮了它們之間的耦合作用,因此,控制方程(17)需改寫為:

在多尺度ESBGK隨機粒子方法(Unified stochastic particle method with ESBGK model,USP-ESBGK)[30]中我們假設對流步式(18a)的碰撞項為:

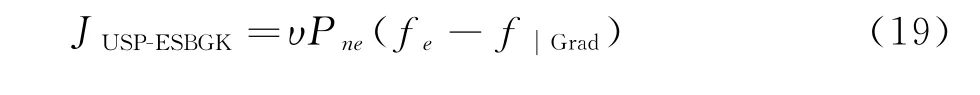
其中Pne＝e－KnGLL,MAX/Knc與當地流動的稀薄程度相關,Knc是Kn數的參考值,KnGLL,MAX是以梯度計算的當地Kn數的最大值[48]。碰撞項(19)中速度分布函數以Grad分布函數近似:

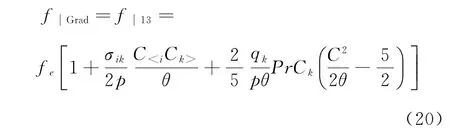
其中θ＝kBT/m,qk為熱流。

形式上看,方程(18)右端兩項將原ESBGK模型的碰撞項分解為兩部分,式(18a)的部分表示碰撞項對連續流動的貢獻,式(18b)的部分表示剩余對非平衡流動的貢獻,而模型方程(18)的多尺度特性可以由Pne表征。當KnGLL,MAX?1時,將JUSP-ESBGK做Chapman-Enskog展開可以發現其一階展開部分與連續流下的碰撞項一致:

因此,隨機粒子運動過程(18a)中分布函數的演化與BGK方程一致,其輸運性質收斂于N-S方程。反之當KnGLL,MAX?1時,JUSP-ESBGK→0,USP-ESBGK方法的控制方程退化到與傳統的SP-ESBGK方法一致,可以準確捕捉小尺度的非平衡流動。

綜上,相比于傳統的DSMC和SP-ESBGK方法,USP-ESBGK方法是一種適用于對跨流域流動問題的多尺度隨機粒子方法。

USP-ESBGK方法與SP-ESBGK方法算法實現的主要區別在對流項式(18a)的求解。數值實現上,USP-ESBGK方法通過引入輔助函數,

并按照梯形公式離散控制方程[36],將對流步式(18a)中對流和碰撞的耦合過程,轉化為求解顯式的分子對流:

因此,類似SP-ESBGK方法,USP-ESBGK方法的主要實現步驟可以概括為:

(1)模擬分子速度和位置的初始化;

(2)構造對流項的輔助分布函數,式(23);

(3)模擬分子位置更新,分子對流,式(24);

(4)模擬分子速度更新,分子碰撞,式(21b);

(5)統計流場宏觀量。如未計算結束,從步驟2繼續下個時間步循環。

步驟(2)中輔助分布函數,可以通過添加滿足速度分布Δt/2JUSP-ESBGK的模擬粒子實現。同時,在步驟4的碰撞過程中添加的模擬粒子被平衡態分布吸收,因此在整個模擬過程中,模擬粒子的總數是守恒的。詳細的計算過程可參考文獻[30]。

2.3 數值算例比較

通過兩個簡單的一維流動,Couette流動和Sod管流,我們將給出DSMC方法與兩種多尺度流動隨機粒子方法的比較。

2.3.1 Couette流動

Couette流動是兩個相反運動的平板驅使的定常流動。上、下平板的運動速度分別為正負Uwall＝10 m/s,兩平板的溫度保持Twall＝273 K。初始時刻平板間的氣體為標準條件(1 atm,273 K)下的氬氣。Couette流動的Kn＝λ/H＝0.01,H為平板間距。對應不同的時間步長,如表1,我們分別計算了DSMC、MTD-FPM和USP-ESBGK的剪切應力值,并給出了與時間步長為0.2Δt/τc時DSMC結果的相對誤差(見括號)。對較小的時間步長,三種方法給出一致的結果。隨著時間步長增加,DSMC的結果逐漸偏離準確值,而MTD-FPM和USP-ESBGK方法的結果并不明顯依賴于時間步長選擇,對較大的時間步長仍然能夠給出正確的剪切應力值。其中MTDFPM計算結果稍大,這是與其較大的普朗特數有關。對跨流域流動而言,各計算區域的稀薄程度可能相差極大的,相異的Δt/τc使傳統隨機粒子方法在不同區域具有不一致的輸運系數。相反,從算例1可以看出,本文提出的改進的BGK/Fokker-Planck模型隨機粒子方法的時間分辨率更高,相比于傳統方法具有較小的數值黏性,因此在計算黏性區域不可忽略的多尺度流動時具有顯著優勢。

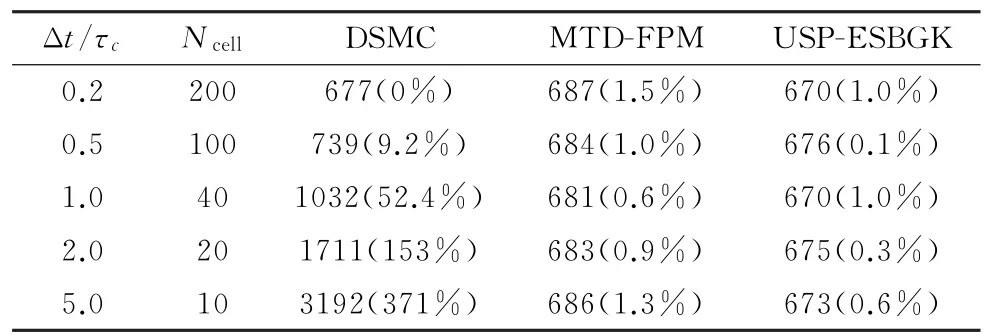
表1 Couette流動計算結果比較(單位：N/m2)Table 1 Comparison of Couette flow results(unit：N/m2)

2.3.2 Sod管流

最后,我們利用MTD-FPM和USP-ESBGK方法計算典型的一維Sod激波管問題[49]。

選取文獻[50]中算例2和算例3,Sod激波管的長度為1 m,左右兩端的邊界取為開放邊界條件。在初始時刻,激波管中間x＝0.5 m處有一個密度間斷,管中的流體為靜止條件。左右兩段間斷區域的初始溫度分別為Tl＝Tr＝273 K。和文獻[51]一致,模擬的時間長度為tfinal＝6.8×10－4s。

其他的計算參數見表2,其中初始時刻左右兩段的密度為ρl和ρr,τc,l為初始時刻激波管左端的平均碰撞時間。兩個算例中,Sod管流Kn數分別在0.01~0.08和0.001~0.008之間變化,因此其是典型的多尺度流動。

表2 Sod管流動的計算參數Table 2 Computational parameter for Sod flows

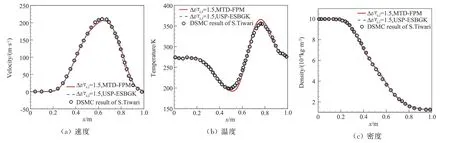
圖2 算例1,Sod管流動的速度、溫度和密度在t final時刻沿管的分布[29-30]Fig.2 Case 1.Velocity,temperature and density at the end time t final for Sod flow[29-30]

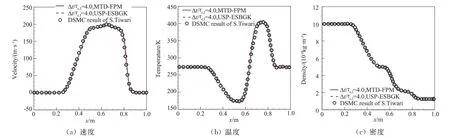
圖3 算例2,Sod管流動的速度、溫度和密度在t final時刻沿管的分布[19-20]Fig.3 Case 2.Velocity,temperature and density at the end time t final for Sod flow[19-20]

圖2和圖3分別給出了算例1和算例2中Sod激波管內tfinal時刻MTD-FPM和USP-ESBGK方法計算的速度、溫度和密度分布,其結果與DSMC方法一致[50]。圖4給出了沿管的時間步長與當地平均碰撞時間的比值,可見流場的稀薄程度是沿管長變化的:從左端至右端,流體從連續區域逐漸過渡到稀薄區域。在DSMC方法中,時間步長一般需小于流場中最小的平均碰撞時間,以保證計算得到物理上準確的流場,而MTD-FPM和USP-ESBGK方法中時間步長的選擇僅需考慮流動特征時間,并不受分子平均碰撞時間的限制,因此通過選取較大的時間步長,兩種多尺度隨機粒子方法可以大大提高跨流域流動的計算效率,例如算例1和算例2中分別選取時間步長為1.5τc,l和4.0τc,l。另外,圖2(b)中,MTD-FPM方法的溫度分布與DSMC的結果存在差異,這是因為在Fokker-Planck方程中普朗特數為1.5,不同于DSMC方法中的值,而ESBGK模型具有正確的Pr,因此溫度分布同DSMC方法也是一致的。

圖4 Sod管流動的時間步長與當地分子平均碰撞時間的比值在t final時刻沿管的分布[19]Fig.4 The ratio of time step and local mean collision time at the end time t final for Sod flows[19]

3 結 論

本文首先總結了傳統隨機粒子方法,如DSMC、FPM和BGK等隨機粒子方法模擬得到的氣體輸運系數的時空離散誤差。DSMC方法計算得到的輸運系數的離散誤差與網格大小/分子平均自由程和時間步長/平均碰撞時間的比值相關。而FPM和BGK隨機粒子方法由于采用速度分布函數的碰撞松弛演化特性來近似碰撞過程,減小了碰撞項的計算量的同時也降低了對網格的限制,但是因為分子運動和碰撞的解耦求解,它們對時間步長的計算要求依然存在,這影響了傳統隨機粒子方法模擬跨流域氣體流動的計算效率。針對隨機粒子方法的這一困難,我們基于Fokker-Planck和BGK模型分別討論了它們的多尺度算法。該方法的主要思想是在碰撞主導的連續流域,通過在分子自由運動計算中耦合連續碰撞作用,反應物理上正確的分布函數演化過程,從而滿足連續流下宏觀的輸運性質。具體來說,分子運動和碰撞即可以通過模擬分子的運動方程耦合;也可以通過分布函數的動理學方程耦合。前者如Fokker-Planck模型中的Langevin方程,通過積分求解該運動方程,并選取合適的松弛系數,可以構造多尺度時間離散的Fokker-Planck模型方法(MTD-FPM)。后者如BGK模型方程,通過對連續流碰撞項的建模和耦合求解,可以構造多尺度的ESBGK隨機粒子方法(USP-ESBGK)。綜合看,這兩種多尺度粒子方法具有如下優勢:

(1)相較于傳統的隨機粒子方法,如DSMC方法,它們的網格大小和時間步長無需滿足分子碰撞尺度(平均自由程和平均碰撞時間)的限制,并在連續流區域滿足宏觀流體力學方程的輸運性質,具有較小的數值黏性,因此對多尺度流動具有更高的計算效率和分辨率;

(2)相對于確定性的離散速度坐標方法,它們無需離散巨大的速度空間,概率性的隨機粒子模擬方法,更適合跨流域高超聲速流動的模擬計算。

(3)它們在算法實現上與DSMC方法類似,可以同DSMC方法耦合計算,從而方便拓展至包含復雜物理和化學過程的跨流域流動問題。