基于網格縮小的非結構網格梯度重構及制造解精度測試與驗證

王年華,張來平,,李 明

(1.中國空氣動力研究與發展中心 空氣動力學國家重點實驗室,綿陽 621000;2.中國空氣動力研究與發展中心 計算空氣動力研究所,綿陽 621000)

0 引 言

自從20世紀中葉計算流體力學(Computational Fluid Dynamics,CFD)誕生以來,隨著計算機技術和計算方法的迅速發展,CFD數值模擬技術已經廣泛應用于以航空航天為代表的諸多領域,革命性地改變了這些領域內傳統的研究和設計方法[1]。但是CFD數值模擬的先天不足在于控制流動的偏微分方程組的可解性以及解的唯一性仍沒有得到理論嚴格證明,因此CFD數值結果的可信度就非常值得關注。

驗證與確認(Verification and Validation,V&V)是評價CFD數值模擬結果可信度的重要手段[2]。驗證的目的在于驗證離散格式、數值方法、程序代碼是否正確地離散并求解了控制方程;而確認的意義在于確認所求解的控制方程及邊界條件是否真實地反映了實際物理流動問題。

20世紀八九十年代,國外就開始對驗證與確認的研究給予高度重視,并逐步開展相關研究工作。1998年,AIAA在總結之前工作的基礎上發布了第一部系統闡述CFD驗證與確認的指南[3]。而國內在驗證與確認研究方面起步較晚,2007年,有學者建議在國內廣泛開展驗證與確認研究,提升國內CFD應用的可信度[4]。

在CFD數值模擬精度的驗證工作中,主要有兩種手段:第一種即通過采用精確解方法[5-6]或制造解方法[7-8],結合網格收斂性測試研究微分方程的求解精度及數值精度階,驗證算法或者求解代碼的正確性。第二種則是通過Richardson插值法[9-10]結合網格收斂性研究進行復雜問題的CFD數值模擬精度驗證。而計算結果的確認,一般采用與高可信度的風洞實驗或飛行試驗結果進行對比,確認計算模型的合理性和準確性。

網格收斂性研究是CFD數值模擬精度驗證必不可少的手段。網格收斂性研究[11]通常是在一系列依次加密的網格上進行數值模擬,并考察計算結果隨網格加密的收斂性;嚴格的網格收斂性研究要求網格自相似加密,即在加密過程中,不改變網格拓撲和網格質量,這樣才能保證計算結果僅僅只受網格尺度的影響。但是自相似加密僅僅能夠在簡單、規則的網格上實現;在一般的網格上,如無黏流模擬中使用的不規則三角形網格,特別是黏性流模擬使用的物面法向存在增長率的各向異性拉伸網格,均難以實現嚴格的網格自相似加密。這樣將導致無法進行嚴格的網格收斂性測試,如果網格加密不恰當,甚至可能無法得到網格收斂解。

在這樣的背景下,Hebert等[12]提出基于網格縮小(Downscaling,DS)的網格收斂性研究方法,并分析了DS方法的優缺點。Diskin等[13]將DS方法應用于一般非結構網格上有限體積離散格式截斷誤差和離散誤差的網格收斂性研究。除此之外,DS方法的應用并不多見。

考慮到黏性流動模擬精度一直是CFD工程應用關注的重點問題之一,以往的研究往往按照一定的規范生成粗中密三套網格,結合Richardson外插法進行網格收斂性研究,這種方法能夠在復雜外形上進行網格收斂性研究,但是由于這些網格加密并不自相似,因此并不能對數值算法的精度階做出嚴格判斷。

本文針對難以實現自相似加密的非結構網格,在典型的各向同性和各向異性拉伸網格上,利用網格縮小精度測試方法分別考察梯度重構精度以及制造解流動模擬精度,驗證網格縮小精度測試方法與網格加密精度測試方法及理論分析的一致性。然后將網格縮小精度測試方法應用到各向異性拉伸網格黏性制造解流動精度測試中考察其優勢。最后還在各向異性拉伸網格上初步考察了梯度重構方法、網格類型對制造解流動模擬精度的影響。

1 數值精度測試方法

離散方法的數值精度由數值誤差(Numerical error,N.E.)定量衡量,在不考慮機器舍入誤差(Round-off error,R.E.)時,數值誤差等于離散誤差(Discretization error,D.E.)。

N.E.＝D.E.＋R.E.≈D.E. (1)

離散誤差產生的原因則是由方程的截斷誤差以及邊界條件的離散誤差直接導致。通常,對于精度階達到p階的離散方法,其離散誤差與網格尺度之間存在以下定量關系:

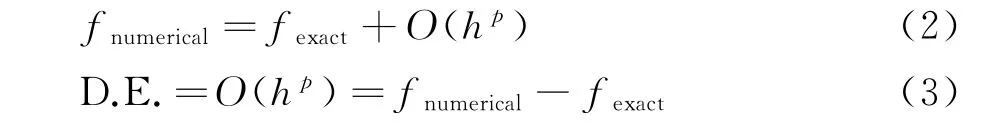
式中h為網格全局尺度,可以定義為[14]:

式中:Vtotal為計算域內所有單元的體積之和,ndof為計算域內自由度數。對于格心型格式,ndof為單元數,d為計算域空間維數。

在本文中,不管是考察梯度重構精度還是制造解流動模擬精度,均是考察離散誤差隨網格尺度的變化情況,考察數值精度階是否與理論精度階吻合,以及不同方法離散誤差的大小比較。

在兩套依次加密的網格上比較離散誤差隨網格尺度h的變化,由式(2)、式(3)可以得到數值精度階的計算公式:

式中:E1和E2分別為加密前后計算域內統計意義的數值誤差,本文考慮離散誤差的L1模,即平均值,h1和h2分別為加密前后計算域內網格尺度。

1.1 網格加密精度測試方法

嚴格的網格收斂性測試不單要求網格全局尺度(式(4))按照一定比例進行縮小,更要求計算域內相應局部網格尺度(如矩形網格的hx和hy)按照統一的比例c進行縮小,以保證每個網格單元在加密的過程中保持其原有的形狀,即網格自相似加密,這樣才能保證在統計誤差計算精度階(式(5))時,兩套網格之間相應網格尺度之比h2/h1＝c為常數,而不是隨著網格單元變化的值,這樣才能得到準確的全局數值精度階。

對于常規的網格收斂性測試,譬如在二維各向同性矩形網格上常常通過將邊界上的節點數加倍來實現網格加密一倍;對于二維各向同性三角形網格,則將每個三角形單元每邊的中點連起來,將原三角形單元剖分成4個自相似的三角形單元,此時網格單元數增加到原來的4倍,相應三維情況網格單元數增加到原來的8倍(金字塔單元為10倍)。比如,對于y方向拉伸比(Stretching Ratio,或增長率)r＝1的無拉伸矩形網格,網格數量為10×10,則將網格數量增加為20×20則可以實現網格加密一倍的目的,如圖1所示。

圖1 傳統網格加密方法示意圖Fig.1 Schematic diagram of traditional mesh refinement

相反,在遇到各向異性拉伸網格時,由于拉伸比的存在,導致不能簡單地通過將節點數加倍來實現網格尺度的統一減小。比如,對于長細比AR＝1×102,y方向拉伸比r＝1.4,網格數量為20×20的各向異性拉伸網格不能通過將網格數量增加為40×40來實現網格加密一倍、網格尺度減小一倍的目的。在一般的非結構網格上,尤其是在各向異性拉伸網格上,通過傳統的自適應方法來加密網格的方法都無法實現嚴格的網格自相似加密,從而導致測得的數值精度階不準確。

1.2 網格縮小精度測試方法

網格縮小精度測試方法不是通過增加網格點數來減小局部網格尺度,而是直接將原有網格進行縮小。比如,原來在[0,1]范圍內均勻分布10個單元的一維網格,網格尺度為0.1。傳統網格加密方法是將網格節點數增加到21,此時單元數增加一倍,網格尺度減小為0.05;而網格縮小方法則是直接將[0,1]范圍的10個單元整體縮小一倍,計算域縮小到[0,0.5]的范圍內,網格單元數不變,網格尺度同樣減小為0.05。

但是,由于網格縮小后,新計算域縮小為原計算域的一部分,因此在統計誤差時,如果僅僅統計新計算域上的誤差,那么會導致網格縮小前后誤差統計區域發生變化,縮小網格上統計得到的誤差不完整。因此,考慮將縮小后的網格在初始計算域范圍內進行隨機平移,取多個在初始計算域內隨機平移的網格樣本,使樣本網格疊加后覆蓋的計算域與初始計算域相同,平均統計所有樣本網格上的計算誤差,得到新網格上的誤差。圖2給出了網格縮小精度測試示意圖,藍色虛線網格為縮小一倍的網格,紅色點畫線網格為隨機平移后的一個誤差統計樣本。

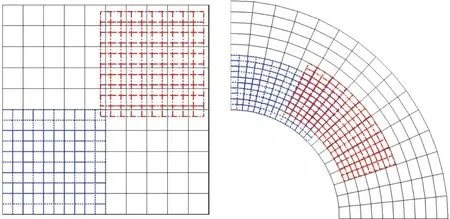
圖2 網格縮小精度測試方法示意圖Fig.2 Schematic diagram of mesh downscaling accuracy tests

由以上的分析可以看到,與傳統網格加密方法相比,網格縮小精度測試具有以下優點:(1)適用于難以進行嚴格自相似加密的一般非結構網格;(2)容易實現并行操作,多個樣本可以同時計算;(3)網格量不大,傳統加密方法網格量呈4倍(二維)或者8倍(三維)增加,但是DS精度測試方法網格量保持不變;(4)不改變初始網格的拓撲和網格質量。

另一方面,盡管網格縮小精度測試方法在一般的非結構網格上存在一些優勢,但是也存在以下一些缺點,比如:(1)重復考慮邊界,Dirichlet精確邊界條件的施加可能會使流動模擬誤差降低;(2)DS方法認為各個網格樣本之間的誤差是獨立的,但實際上,不同樣本之間的誤差會互相影響;(3)雖然多個樣本可以并行操作,但是總計算量較大。

2 DS精度測試方法的驗證

由上述的分析可知,DS網格樣本數量要足夠大,以滿足“樣本網格覆蓋的計算域與初始計算域相同”的要求。但是在流動模擬精度測試時,也要注意到,每個樣本網格上的數值模擬均采用了精確的Dirichlet邊界條件,樣本數量過多不僅可能使樣本統計的誤差低于真實誤差,也增加了計算量。通過與傳統網格加密方法對比驗證,本文所有的DS精度測試均取100個樣本。事實上,我們比較過不同樣本數的影響,發現樣本數大于50后,樣本數量對計算結果基本沒有影響。由于驗證過程比較簡單,加之篇幅限制,在此不再贅述。

本節主要考察3種情況:各向同性網格梯度重構精度測試、各向異性拉伸網格梯度重構精度測試、各向同性網格制造解流動精度測試[15],將DS精度測試結果與傳統網格加密精度測試結果及附錄中的梯度重構模板理論分析結果進行對比,驗證網格縮小精度測試方法在各向同性網格、各向異性網格上精度測試結果的準確性。

2.1 各向同性網格梯度重構精度

梯度重構采用的測試函數形式為:

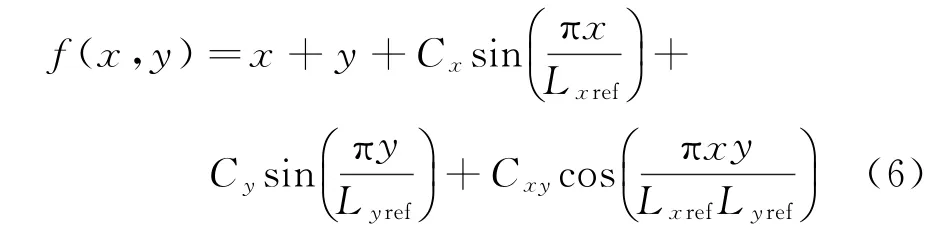
該流場函數包含參考尺度Lxref、Lyref,加權系數Cx、Cy、Cxy以及線性項以確保梯度場不存在零點,可以模擬多種光滑的梯度場,可根據不同的測試需求進行選擇參考尺度及加權系數。本文取Cx＝Cy＝Cxy＝1.0,Lxref＝Lyref＝30。

本文重點考察基于格林-高斯(Green-Gauss)公式的梯度重構GG-Cell方法[15-17],該方法面心值采用單元值算術平均求解,在非規則網格上精度會降階至0階[17];以及采用基本模板、加權的最小二乘梯度重構方法,記為WLSQ-basic[15-18]。

分別采用傳統網格加密方法和網格縮小方法測試GG-Cell梯度重構方法在以下兩種網格(圖3)上的精度及精度階。

(1)Grid 1矩形網格:傳統網格加密方法采用5套依次加密的矩形網格,網格數量分別為20×20,40×40,80×80,160×160,320×320;DS測試方法的初始網格為20×20。

(2)Grid 2擾動四邊形網格:即在矩形網格的基礎上,引入網格節點位置的隨機擾動,隨機擾動量定義為rh/4,其中r是[-1,1]區間內的隨機數,h是局部網格尺度。

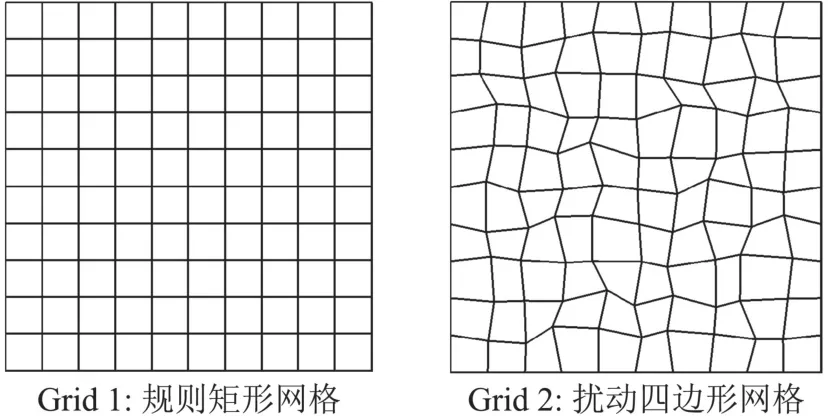
圖3 精度測試各向同性網格Fig.3 Isotropic grids for accuracy tests

傳統網格加密方法和DS方法測試得到的x方向梯度離散誤差如表1和表2所示。

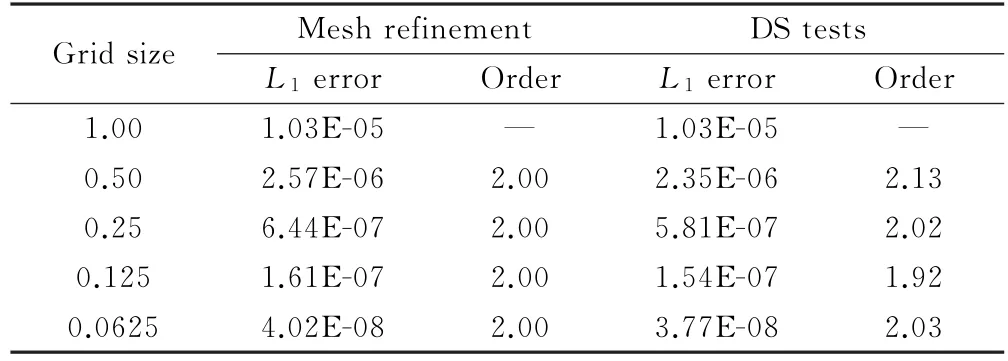
表1 網格加密精度測試與DS精度測試離散誤差的比較(Grid 1：規則矩形網格)Table 1 Comparison between mesh refinement tests and DS tests(discretization error of x-direction gradient on Grid 1)

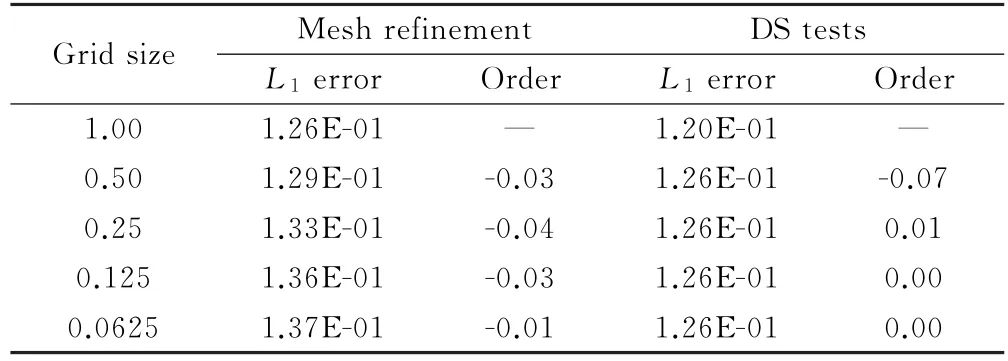
表2 網格加密精度測試與DS精度測試離散誤差的比較(Grid 2：擾動四邊形網格)Table 2 Comparison between mesh refinement tests and DStests(discretization error of x-direction gradient on Grid 2)

結果顯示,DS方法的離散誤差略小于網格加密方法的誤差,這是因為盡管DS方法樣本數量較大,但是縮小后的網格樣本并不一定能夠完全覆蓋初始計算域,即DS方法統計誤差的區域與網格加密方法統計誤差的區域存在一定差異,因此統計到的誤差也存在一定的差異。但是這并不影響對精度高低的判斷以及數值精度階的計算,如在矩形網格Grid 1上,如表1所示,兩種方法測得的精度階(按式(5)計算)均為2階。而在擾動網格Grid 2上,如表2所示,兩種方法測得的精度階均為0階,其主要原因是在擾動網格上面心值插值精度無法達到二階。文獻[17]對GG-Cell方法在擾動網格上精度降階的原因做了詳細解釋,在此不再贅述。因此,在各向同性網格梯度重構精度測試中,DS精度測試方法能夠得到與傳統網格加密方法一致的結果。

2.2 各向異性拉伸網格梯度重構精度

正如第1節中所述,對于各向異性的拉伸網格,無法通過加密網格點數來實現嚴格的網格自相似加密,從而導致無法通過傳統的網格加密方法來準確測試各向異性拉伸網格上各種離散格式的精度階。

在此,為說明傳統網格加密方法在各向異性拉伸網格上無法準確測試方法的精度階,以下給出采用傳統網格加密方法測試得到的離散誤差和精度階。傳統網格加密方法采用5套依次加密的各向異性拉伸矩形網格,第一層網格長細比AR＝1×102,網格數量分別為20×20,40×40,80×80,160×160,320×320,保持計算域大小不變,顯然這樣在加密的過程中,網格的拉伸比r會發生改變,各套網格的拉伸比分別為:r＝1.4,r＝1.18,r＝1.085,r＝1.04,r＝1.02,其中第一套20×20的網格如圖4所示。

圖4 精度測試的各向異性拉伸矩形網格Fig.4 Anisotropic stretched quadrilateral grids for accuracy tests

表3和表4分別給出了GG-Cell梯度重構和WLSQ-basic梯度重構方法在各向異性拉伸網格上的離散誤差和精度階,測試方法為網格加密方法。

結果顯示GG-Cell和WLSQ-basic方法在x、y兩個方向均能達到二階精度,顯然,該結果與附錄中各向異性梯度重構模板分析的結論不一致,模板分析結果顯示GG-Cell方法在x方向可以達到二階精度,但是在y方向降階至0階精度;WLSQ-basic方法在x方向可以達到二階精度,但是在y方向也只能達到一階精度。可以看到,傳統網格加密方法在各向異性拉伸網格上是不適用的,測得的結果也是錯誤的。

由于傳統方法在各向異性拉伸網格上不適用,因此以下采用20×20、第一層網格長細比AR＝102、拉伸比r＝1.4的各向異性拉伸矩形網格作為初始網格,對GG-Cell梯度重構方法和WLSQ-basic方法進行DS精度測試。測試函數仍然為光滑非線性函數式(6)。

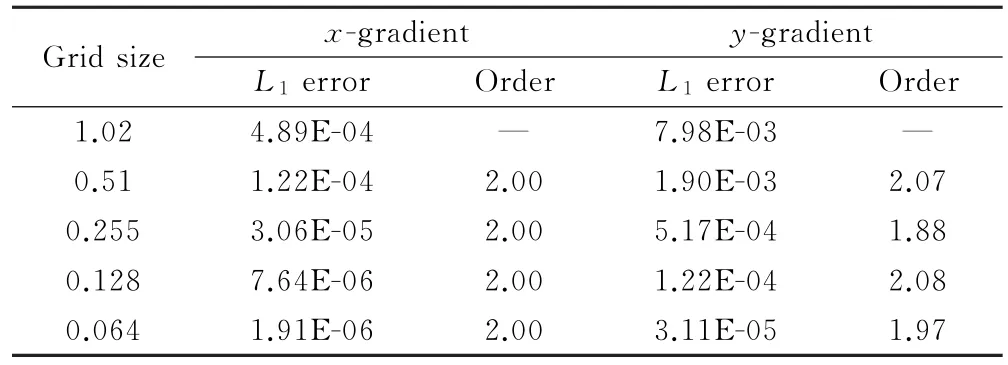
表3 網格加密精度測試的離散誤差與精度階(GG-Cell)Table 3 Discretization error and accuracy order of mesh refinement tests(GG-Cell)

表4 網格加密精度測試的離散誤差與精度階(WLSQ-basic)Table 4 Discretization error and accuracy order of mesh refinement tests(WLSQ-basic)

表5和表6分別給出了GG-Cell梯度重構方法和WLSQ-basic梯度重構方法在各向異性拉伸矩形網格上的離散誤差和精度階。結果顯示,在x方向,GG-Cell和WLSQ-basic均能達到2階精度;而在y方向,GG-Cell降階至0階精度,而WLSQ-basic仍然保持1階精度。這與附錄中的模板分析結果是完全一致的,因此這體現出DS方法在各向異性拉伸網格計算精度測試與驗證上的優勢。

表5 DS精度測試的離散誤差與精度階(GG-Cell)Table 5 Discretization error and accuracy order of DS tests(GG-Cell)

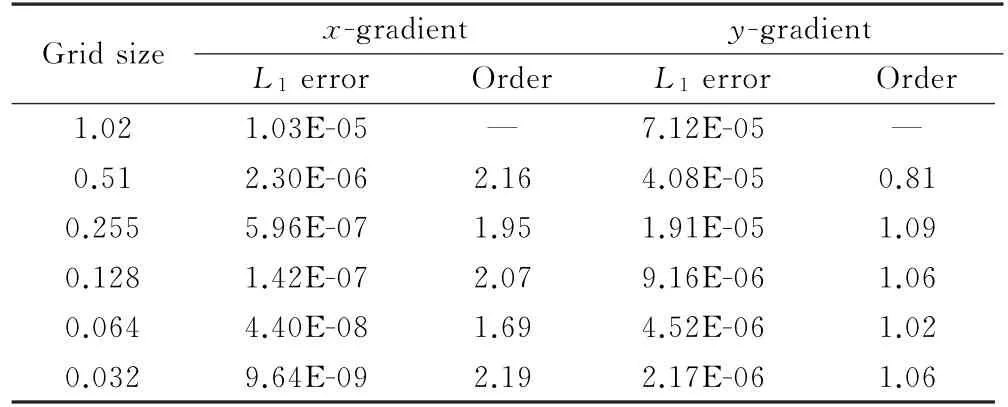
表6 DS精度測試的離散誤差與精度階(WLSQ-basic)Table 6 Discretization error and accuracy order of DS tests(WLSQ-basic)

2.3 各向同性網格制造解流動模擬精度

制造解方法[7-8]是驗證的重要手段,與精確解方法需要確定控制方程組的精確解(解析解)不同,制造解方法通過人為設計“制造解”,將制造解代入原始的控制方程得到修正的控制方程,制造解即為修正方程的精確解,數值求解修正控制方程得到數值解,通過比較數值解與制造解的差值即可量化離散誤差。文獻[15]對制造解方法在代碼驗證、精度分析、邊界條件驗證等方面的應用作了詳細描述,并實現了分量制造解方法和標量制造解方法。

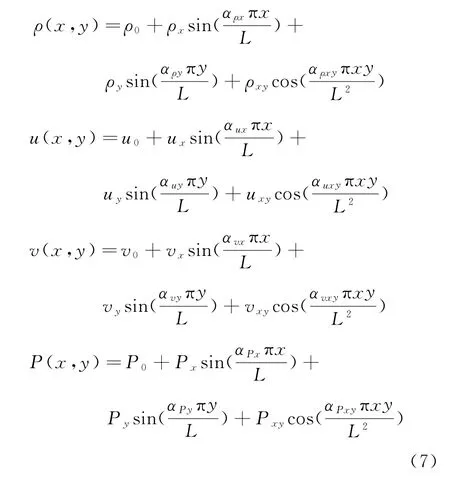
本文采用2.1節中圖3所示的矩形網格Grid 1和擾動四邊形Grid 2,采用Euler分量制造解進行精度測試,制造解形式為式(7),采用的是“名義”上二階精度的有限體積格式,即網格交界面上的物理量通過單元中心的物理量平均值線性展開得到。方法具體實現可參考文獻[15,19]。本算例梯度重構方法采用GG-Cell方法,無黏通量格式選擇Roe格式。比較傳統網格加密方法與DS精度測試得到的密度離散誤差和精度階。

表7和表8分別給出了矩形網格(Grid 1)和擾動四邊形(Grid 2)上網格加密精度測試及網格縮小精度測試得到的密度離散誤差及相應精度階。結果顯示在規則矩形網格上,制造解模擬精度能夠達到二階精度,而在擾動網格上,流動模擬精度降階至一階精度,網格加密精度測試與DS精度測試得到完全相同的精度階;在離散誤差的絕對大小上,DS方法與傳統網格加密方法也比較接近,這進一步證實了DS方法在流動模擬精度測試上的有效性。擾動網格上流動模擬精度降階是因為GG-Cell梯度重構在擾動網格上精度下降至0階,詳細分析可參考文獻[17]。

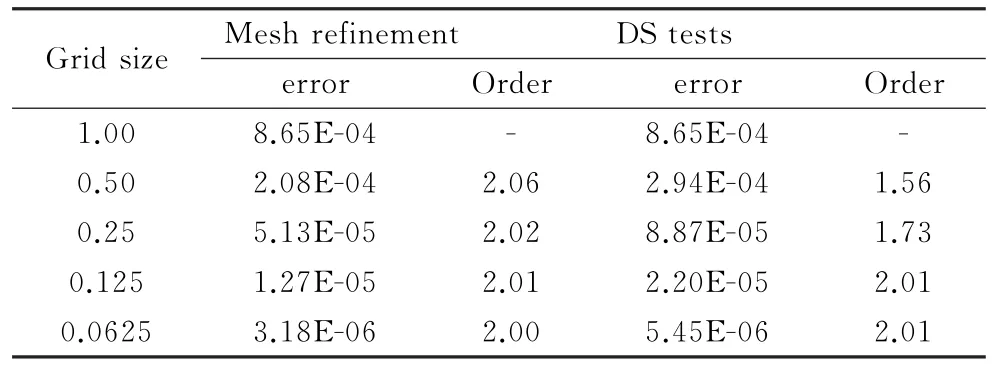
表7 網格加密精度測試與DS精度測試的比較(Grid 1)Table 7 Comparison between mesh refinement tests and DS tests(density discretization error of Euler manufactured solution on Grid 1)

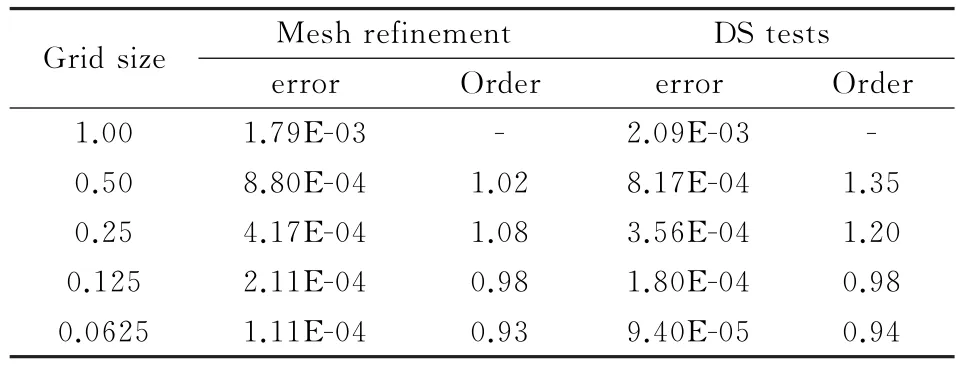
表8 網格加密精度測試與DS精度測試的比較(Grid 2)Table 8 Comparison between mesh refinement tests and DS tests(density discretization error of Euler manufactured solution on Grid 2)

3 各向異性網格流動模擬精度測試

經過第2節中三個算例的驗證,證實了DS精度測試方法在各向同性網格和各向異性網格上的可行性和有效性,以下將DS精度測試方法應用于圖4所示的各向異性拉伸矩形網格,對其進行對流擴散方程的標量制造解[15]DS精度測試,采用對流擴散方程是為了考慮擴散項,即黏性項的作用。對流擴散方程形式為式(8),各項系數為a＝b＝c＝1,ν＝1×10－4,標量制造解形式為式(9)。

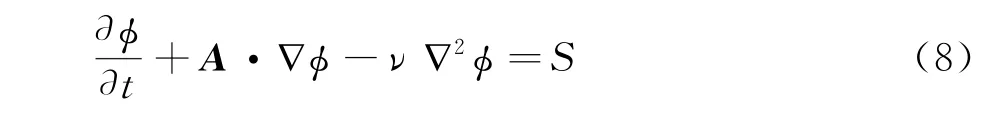
式中?為任意標量場,A＝(a,b,c),A和ν分別為線性對流項和線性擴散項的常系數。

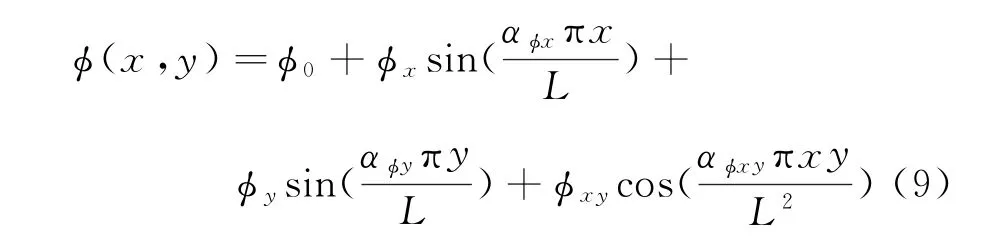
梯度重構方法分別選擇GG-Cell和WLSQ-basic,根據2.2節中的梯度重構精度測試結論,在各向異性拉伸網格y方向上,GG-Cell方法精度下降到0階,而WLSQ-basic方法仍然保持一階精度,因此可以預測GG-Cell和WLSQ-basic的制造解流動模擬精度分別為一階和二階。

表9給出了兩種梯度重構方法在各向異性拉伸矩形網格上的制造解流動數值離散誤差及相應的精度階,DS測試結果與預期完全吻合。對于傳統方法無法自相似加密的各向異性拉伸網格,DS精度測試方法顯示出其優勢。

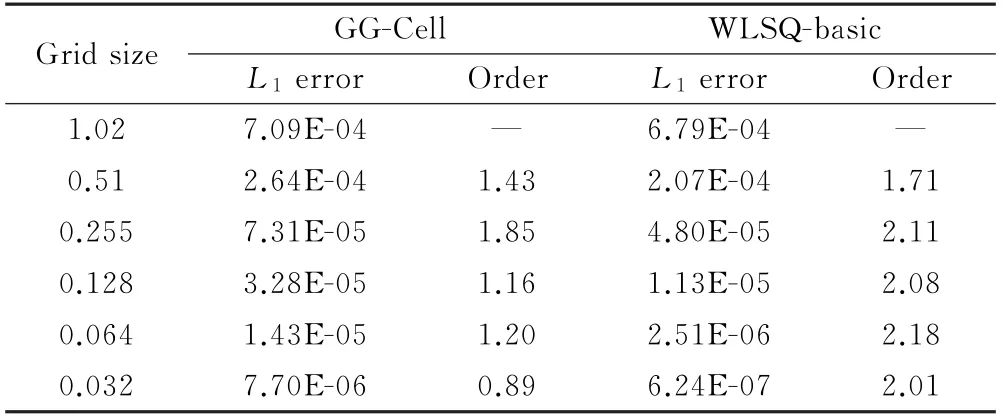
表9 DS精度測試的離散誤差與精度階(各向異性拉伸矩形網格)Table 9 Discretization error and accuracy order of DS tests(anisotropic stretched quadrilateral grids)

最后,在圖5所示的各向異性拉伸三角形網格上進行與各向異性拉伸矩形網格類似的精度測試。梯度重構方法仍然選擇GG-Cell和WLSQ-basic方法。

圖5 精度測試各向異性拉伸三角形網格Fig.5 Anisotropic stretched triangular grids for accuracy tests

表10給出了兩種梯度重構方法在各向異性拉伸三角形網格上的制造解流動數值離散誤差及相應的精度階。結果顯示GG-Cell方法只有一階精度,已經不滿足二階有限體積離散的精度要求,而WLSQ-basic則仍然保持二階精度,且離散誤差明顯比GGCell方法離散誤差小。

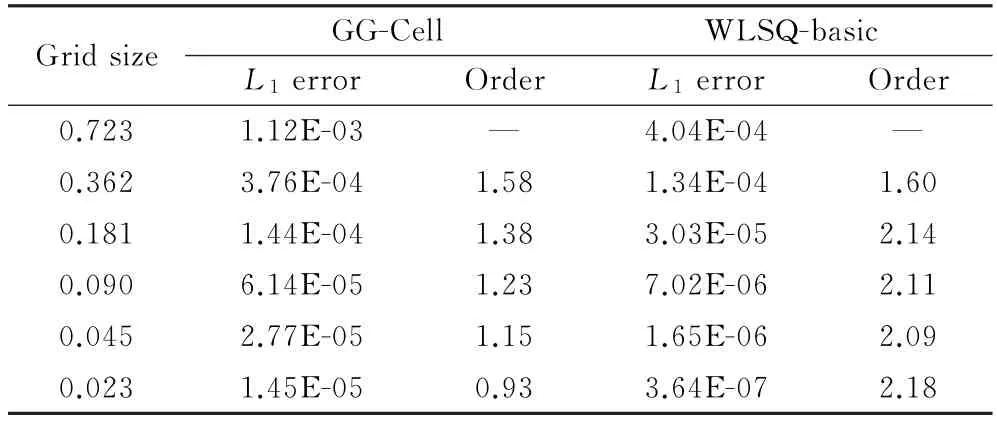
表10 DS精度測試的離散誤差與精度階(各向異性拉伸三角形網格)Table 10 Discretization error and accuracy order of DS tests(anisotropic stretched triangular grids)

進一步還可比較四邊形網格與三角形網格離散誤差的大小,比較結果如圖6所示。結果顯示,在同等的網格尺度情況下,采用GG-Cell方法時,矩形網格精度更高,而在采用WLSQ-basic方法時,矩形網格和三角形網格精度相差不大。

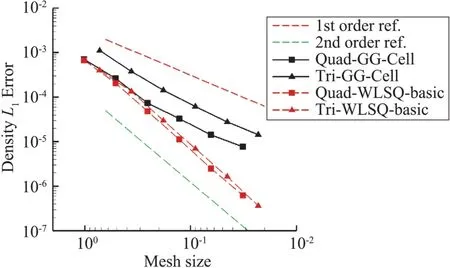
圖6 矩形網格與三角形網格精度的比較Fig.6 Comparison between quadrilateral grids and triangular grids on solution accuracy

但是,如果從計算效率的角度來看,一個四邊形網格可以剖分為兩個三角形,因此整體的網格數量僅為三角形網格的1/2,因此計算效率更高。因此,在實際應用中,結合網格生成的易用性和黏性流動的模擬精度和效率,大多采用混合網格[20]。

4 結 論

本文實現了基于網格縮小的精度測試方法,在各向同性網格梯度重構精度測試、各向同性網格無黏制造解流動精度測試,及各向異性拉伸網格梯度重構精度測試等三類算例中,將網格縮小測試結果與傳統網格加密精度測試結果和理論分析結果進行對比,驗證了網格縮小精度測試方法的可行性和有效性。

進一步將網格縮小精度測試應用于傳統方法無法處理的各向異性拉伸網格黏性制造解流動精度測試,得到了與預期中完全一致的精度階結果,證明網格縮小精度測試方法適用于更一般的非結構網格的精度測試。

此外,本文還初步考察了梯度重構方法、網格類型對黏性制造解流動模擬精度的影響。結果顯示GG-Cell在各向異性拉伸網格上會導致流動模擬精度降階,在相同網格尺度下,離散誤差顯著增大;而WLSQ-basic方法則能夠保持流動模擬精度達到二階。在采用GG-Cell方法時,四邊形網格精度更高,而在采用WLSQ-basic方法時,三角形網格能夠達到與四邊形網格相當的計算精度,但是三角形網格計算效率更低。

需要指出的是,雖然GG-Cell梯度重構方法的精度在各向異性網格上會降至0階,但是由于空間離散采用了線性重構,因此其計算結果的絕對誤差仍較真正的一階格式(單元內常值分布)小。另一方面,由于梯度重構精度未達到一階以上精度,因此雖然采用了“名義”上的二階有限體積離散格式,但是其實際數值精度階會達不到理想的二階精度。這正是我們希望避免的。

下一步可以將網格縮小精度測試方法應用于更一般的非結構網格精度測試,同時,也可以作為精度測試工具,詳細定量考察不同網格類型、網格質量對數值模擬精度的影響。在此基礎上,實際黏性流動模擬精度測試、驗證與計算精度的提高也是值得深入研究的方向。

附錄A 網格模板梯度重構精度分析

模板分析是在特定梯度重構網格模板上,分析在不同梯度重構方法對解析函數的梯度重構精度。本節將基于格心型格式,在典型的各向異性網格模板上分析兩種常用梯度重構方法(GG-Cell和WLSQ-basic)的重構精度。具體來說,采用非線性函數f(x,y)＝sin x＋sin y＋cos(x y)作為重構測試函數,考察各向異性網格上的梯度重構離散誤差(即重構梯度與精確梯度的差值)。

A.1 各向異性四邊形網格

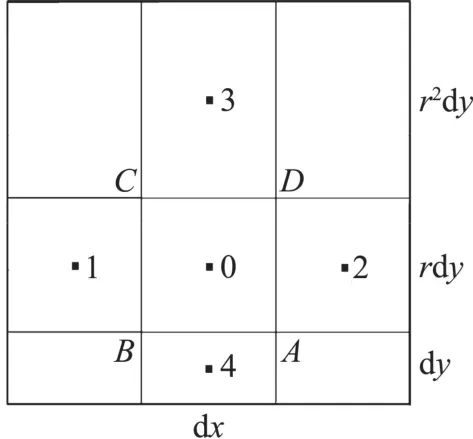
基于格心型格式,選擇如圖A.1所示的各向異性四邊形網格進行模板梯度重構精度分析,第一層網格長細比(Aspect Ratio)為AR＝d y/d x,網格拉伸比(或網格增長率,Stretching Ratio)為r,圖A.1中點0為梯度待求點,坐標假設為(x,y),點1~點4均為梯度重構模板點,其坐標容易確定,在此不再列出。表A.1給出了GG-Cell和WLSQ-basic方法的在各向異性四邊形網格上的梯度重構誤差。格心位置為(x,y)的網格單元,其梯度重構誤差是網格長細比AR,拉伸比r及網格尺度d y的函數,對于各向異性網格,AR?1,r接近1。

當拉伸比r＝1,即網格無拉伸時,顯然兩種梯度重構方法均能達到二階精度,梯度離散誤差的量級為O(d y2),但是值得注意的是網格尺度較大的x方向離散誤差的量級為O(AR2d y2)＝O(d x2),而y方向的離散誤差的量級為O(d y2),并不受AR的影響,當AR?1時,盡管兩個方向上的離散誤差均呈現出二階精度,但是網格尺度較大的x方向絕對誤差將會遠大于y方向,梯度重構精度呈現出各向異性的特性。

而當拉伸比r≠1時,顯然GG-Cell方法在x方向仍然呈現出二階精度(梯度離散誤差的量級為O(AR2d y2)＝O(d x2)),這是因為網格在x方向上是均勻的;而在拉伸的y方向,GG-Cell梯度重構精度下降到0階(梯度離散誤差的量級為O(1))。相反,此時WLSQ-basic方法在x方向呈現出二階精度,y方向則呈現出一階精度,不會出現精度降階至0階的情況。由于梯度重構只跟局部重構模板相關,以上的模板分析結論是嚴格的,可以為本文2.2節提供參考。

圖A.1 梯度重構測試四邊形網格模板Fig.A.1 Quadrilateral grid stencils for reconstruction tests

表A.1 不同梯度重構方法的離散誤差(各向異性四邊形網格)Table A.1 Discretization errors of different reconstruction methods(anisotropic quadrilateral grid stencils)