氣體稀薄效應對熱流計算的影響

陳 杰,張家騏,歐吉輝

(天津大學 機械工程學院 高速空氣動力學研究室,天津 300072)

0 引 言

臨近空間高超聲速飛行器的研發在中國及世界范圍內已受到越來越多的關注,但同時也面臨著巨大的技術挑戰和新的科學問題[1-3]。周恒和張涵信在他們所寫的《空氣動力學的新問題》一文[1]中分析了在情況下現有的空氣動力學的不足,提出了若干需要考慮的新問題,其中之一就是如何考慮流場中可能出現的局部稀薄氣體效應。他們分析了臨近空間高超聲速飛行器的邊界層,指出:由于邊界層中溫度很高,再加上臨近空間飛行器的飛行高度很高,因此邊界層中的氣體密度可能很低,即氣體分子自由程較大。另一方面,邊界層中的剪切很強,在這兩個因素的影響下,邊界層中法向相隔一個分子自由程的兩層流體的速度差和當地的分子運動的平均速度相比不是一個小量,這會導致分子運動的速度分布函數顯著偏離Maxwell分布,使得現有的各種基于實際分子自由運動速度的分布函數對Maxwell分布僅有小的偏離假設下提出的分析計算方法不再可靠,需要尋找新的方法。根據這一思想,陳杰和趙磊在文獻[2]中提出了對應的參數Zh,用以刻畫氣體稀薄效應對剪應力的影響。

參數Zh定義為:相隔為一個分子自由程的兩層流體的宏觀速度差和分子熱運動速度之比。這是一無量綱參數,即:

在臨近空間高超聲速飛行器的設計中,不僅要考慮氣動力,還要考慮氣動熱[3,6-10]。對于長時間在近空間中以高超聲速機動飛行的飛行器,精確的熱環境預測對低冗度熱防護設計十分重要[6]。臨近空間高超聲速飛行器氣動加熱受稀薄氣體效應、高溫真實氣體效應、飛行器復雜外形帶來的復雜流場結構等多種因素的影響[7-10]。工程上往往針對駐點熱流基于半經驗參數構建橋函數等方式考慮稀薄非平衡計算[11]。在數值計算方面也發展了多種考慮稀薄效應的宏觀方程模型[11-15]。

本文將在之前研究強剪切流中稀薄效應對應力計算工作的基礎上[2,4-5],進一步考慮氣體稀薄效應對熱流計算的影響,將研究以下問題:1)存在強溫度梯度時,氣體的稀薄效應如何分析和處理,分子速度分布函數是否還是Maxwell分布,如果不是,刻畫偏離程度的無量綱參數是什么;2)如果該參數的值大了,會如何影響熱流計算?傅里葉導熱定律是否成立?是否能定量地找到等效導熱系數和此參數的依賴關系。研究的路線和文獻[2]相同,即以DSMC為手段尋找氣體有稀薄效應下的熱傳導規律。3)初步驗證將該規律納入CFD計算中是否可以有效改善受稀薄效應的熱流計算?

1 計算模型

1.1 一維導熱問題

為單純研究存在強溫度梯度時氣體稀薄效應對熱流計算的影響,選取無宏觀流動的導熱問題進行分析。我們這里想要獲得的是對于具有一定稀薄程度的氣體在存在強溫度梯度時,傅里葉定律所計算的熱流誤差,而不考慮壁面引起的效應。如圖1(a)所示,該研究對象為距壁面較遠且存在強溫度梯度的流體,即在厚度L的薄層內存在較大的溫度差Th－Tc。經典的兩平板間導熱問題如圖1(b)所示,相距L的兩板分別保持不同的溫度Tc、Th,壁面邊界條件通常采用Maxwell完全漫反射條件。對于圖1(b)所示問題,可基于兩板間距定義傳統Knudsen數KnL＝λ/L。如果KnL較小,如KnL＜0.1,兩板間中心區域可認為不受固壁邊界條件影響,等價于圖1(a)中所要研究的薄層。但隨著KnL增大,壁面效應越明顯,中心區域的熱流計算將既受到強溫度梯度的影響,也受到壁面影響。雖然可以通過增大兩板間的距離減弱壁面效應,但是當兩板距離L增大后,如在中心區域實現相同的溫度梯度d T/d x,兩板的壁面溫度之差就要相應地增大,很難實現。如保持中心溫度不變,一端溫度甚至可能小于0°,顯然不合理。如要求一端保持不低于0°,則另一端溫度就非常高。即便這樣也不容易實現較大ZhT時的情況。因此本文將通過在虛線處施加合適的邊界實現圖1(a)中所示問題的模擬。

圖1 一維導熱問題Fig.1 1D conduction

1.2 DSMC方法

本文采用基于Bird提出的標準DSMC算法[16]建立的自編程程序。作為第一步,為避免高溫下可能引起的分子振動能被激發,甚至導致分子離解等復雜問題掩蓋氣體稀薄效應的本質問題,本文考慮單原子氣體氬氣作為模擬氣體,采用硬球模型。氬氣分子質量為6.63×10-26kg,直徑為3.659×10-10m。

DSMC方法使用大量的模擬分子模擬真實的氣體,用一個模擬分子代表一定數量的真實氣體分子,該方法的本質是在時間步長Δt內,對分子的運動和分子間的碰撞進行解耦,要求時間步長小于平均碰撞時間,網格尺度小于平均自由程。因此,為保證計算有效導熱系數的足夠精確,采用了文獻[17]中建議的網格大小和時間步長。為獲得統計噪聲較小的熱流以及更準確的等效導熱系數,模擬使用了大量的模擬分子,初始每個網格內分子數為1×100個,對導熱穩定后的106個時間步進行統計平均。

1.3 稀薄效應刻畫參數

周恒和張涵信[1]指出:相隔一個分子自由程的兩層間的分子碰撞是產生剪切力和熱傳導的主要機制。在剪切流中,刻畫稀薄效應的無量綱參數Zh為一個分子自由程上宏觀速度的差與微觀分子最可幾速度之比。該參數有效表征了剪切流中的非平衡。根據同樣的思想,這里將該參數類推至溫度,流體的溫度是分子平均熱速度的統計。如果一個分子自由程上分子熱運動速度的改變量與熱運動平均速度本身相比不再是小量,那分子速度分布也不再會是Maxwell分布。

因此,定義ZhT為相隔一個分子自由程的兩層流體的特征分子熱速度梯度和當地的平均熱速度之比為ZhT:

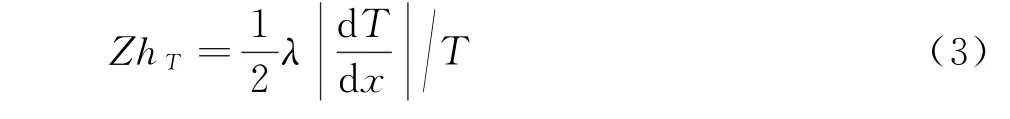
需要指出的是ZhT的形式雖然與文獻[18]中的KnGLL-T只差一個常數,但是意義不同。這里是兩個速度或者溫度之比,而文獻里KnGLL-T的意義為兩個長度之比,即分子平均自由程與溫度的標尺長度之比。ZhT參數的物理意義將在2.1節中通過對速度分布函數的分析進一步詳細解釋。

1.4 邊界條件

這一節探討邊界條件的實施。如1.1節所示,我們需要采用合適的邊界條件模擬距壁面較遠且存在強溫度梯度的一層流體。在稀薄強溫度梯度條件下,氣體顯然不可能處于平衡態,即在DSMC模擬的邊界處不能通過平衡態Maxwell分布向計算區域加入粒子。為此,我們提出了新的邊界條件以實現邊界處所設定的溫度以及粒子所處的非平衡特性。

該邊界條件的主要思想是對于不受壁面影響的導熱問題,模擬區域邊界處與中心點具有相似的非平衡性,即分布函數形狀以及偏離Maxwell分布的程度相同,因此通過中心點的粒子信息在邊界處進行重構,使其與中心點具有相似非平衡態分布函數,但兩組粒子的統計溫度不同。在下文將此邊界稱為“非平衡克隆邊界”。其具體實現方法分以下幾個步驟:在每一次時間步推進后,1)統計邊界網格中存在的粒子數,用N表示;2)從中間網格隨機抽取N個分子復制到邊界網格。對低溫端,由于對應的溫度低,所以一般N要大于中間網格的粒子數,需要另外隨機抽取若干粒子,補足差數;3)統計抽取的這N個粒子重新組成的粒子團的平均速度。因為隨機性,重新組成的粒子團平均速度可能不再是0,有很微小的偏差。因此需要將這個小的偏差速度減掉,以免造成邊界處不正確的動量輸入;4)統計N個粒子的溫度T1,根據壁面設定的溫度Tw和這個統計溫度比重整粒子的速度,即粒子速度乘以。這樣,壁面網格內的分子平均速度為0,溫度為Tw,分子的速度分布函數與中間網格類似。

圖2 概率密度分布函數Fig.2 Probability density function

為驗證此邊界,我們分別模擬了圖1所示兩種情況。對于圖1(a)所示模型,Tc＝700 K,Th＝1200 K,L為中心點平均自由程的5倍,兩邊均用克隆邊界。對于圖1(b)所示模型,Tc＝400 K,Th＝2000 K,中心點附近溫度為1200 K,為避免壁面影響,L為中心點平均自由程的10倍。圖2給出了兩個計算模型相同溫度1200 K處的概率密度分布函數(Probability Density Function,PDF),并與1200 K的Maxwell分布對比。可以看到圖1(a)模型中克隆邊界條件所實現的分布函數與圖1(b)模型中心點的溫度函數重合,且相同程度地偏離了平衡態,驗證了克隆邊界可以重構不受壁面影響的非平衡態分布函數。峰值微弱的差別來自于溫度的差,克隆邊界處溫度為1200 K,中心點附近所取的點溫度為1197 K。

1.5 等效導熱系數

本文最終要獲得的是ZhT對熱流計算的影響,求得等效的導熱系數,其定義為:

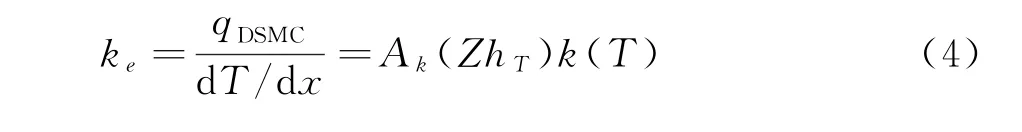
即DSMC獲得的熱流比上當地的溫度梯度,可理解為氣體在線性本構關系假設下所表現的等效導熱系數,它是傳統的導熱系數乘以修正系數Ak(ZhT)。

2 結果分析

2.1 速度分布函數

我們計算了不同ZhT的參數下計算區域中心點的概率密度分布函數(PDF)。隨著ZhT的增加,分布函數逐漸偏離Maxwell分布。不同于剪切流中分布函數呈現單峰、雙峰、三峰等多種形態[2],導熱問題中不同ZhT的參數下分布函數偏離的形態是一致的,如圖3所示,只是偏離程度不同。圖3給出了ZhT＝0.03和ZhT＝0.1時的概率密度分布函數。ZhT＝0.03時分布函數的峰值已經開始向右傾斜,ZhT＝0.1則明顯偏離。

從分布函數與Maxwell分布對比來看,粒子運動的最可幾速度不再是零而變為正。其原因可分析如下:設圖4中的A、B線分別為一個網格的兩個邊界,溫度梯度方向為從A向B,即B處的溫度高于A處的溫度,用NA、NB分別表示在網格線上進出的粒子數目。由于氣體宏觀靜止,因此在網格線處,單位時間從左往右和從右往左穿過的粒子數應相等,即圖中所示的＝,＝。設c－為分子熱運動平均速度,則可認為在一個時間步長d t內,位于B或A兩側一個寬為的范圍內的正向或反向運動的粒子在d t時間內均可分別向左或向右穿過網格線,對初始的Maxwell分布來說,正向和反向的粒子數應相等。而位于該范圍的粒子數則和密度與成正比。由于密度和溫度成反比,而則與成正比,因此在d t時間內穿過網格的粒子數應該和1/成正比。由于B處的溫度比A處的溫度高,所以B處穿過網格的粒子數小于A處穿過網格的粒子數,也就是圖中所標示的,即有凈流入的正向粒子和凈流出的反向粒子,使得分布函數偏于正的一側。

圖3 概率密度分布函數Fig.3 Probability density function with different Zh T parameters

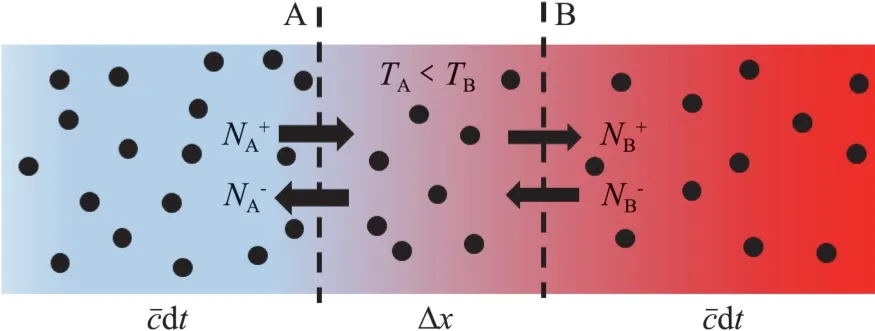
圖4 粒子輸運示意圖Fig.4 Schematic diagram of particle transport

根據以上分析,單位時間內一個網格的正向粒子凈流入量和通過中心界面的正向粒子流量之比,即:

可以刻畫分布函數偏離Maxwell分布的程度。而這一參數和公式(3)的定義一致。

我們還可從DSMC的計算過程中做統計以證實這一趨勢。在計算中心點網格溫度為1000 K,網格內模擬粒子數在100個左右,等導熱穩定后我們對中心點網格低溫側和高溫側進出的粒子在1×106時間步上進行統計平均。如圖3(a)所示的ZhT＝0.03的情況,中心點網格低溫側進出的粒子均為5.4088個,而高溫側進出的均為5.3893,即網格內總的進出粒子相等,但低溫側進入的比右側多0.36%。圖3(b)所示的ZhT＝0.1的情況,低溫側進入的比高溫側多0.42%,當ZhT＝0.36時低溫側進入的比高溫側多0.52%。因此,ZhT越大,網格中來自低溫側的粒子比來自高溫側的粒子越多。不過DSMC的結果是最終平衡態的結果,當數量更多的正向粒子進入網格后,會和反向運動的粒子發生碰撞,使得正反向的粒子數趨于相等(正向粒子數雖然較多,但平均速度較小,網格內粒子之間相互碰撞的總的效果是使得粒子數和大小趨于相等,和輸入粒子的作用相反)。這是一個十分復雜的過程,很難用簡單的物理過程說清楚。

2.2 壁面效應分析

本節主要分析壁面效應的影響,以及驗證克隆邊界是否能夠有效消除壁面影響。對同一問題,如果使用完全漫反射條件,即所模擬的問題為受限于間隔距離很小的兩平板間的導熱問題,壁面附近氣體的溫度與給定的壁面溫度不相等,即所謂的溫度跳躍,壁面附近努森層中的溫度分布也呈現非線性變化,如圖5黑線所示。如果采用克隆邊界,溫度分布則如黑點所示,可基本實現所施加的溫度梯度,且成近似線性分布。在靠近壁面的一個點處有一個小的間斷,但這并不影響我們在中心區域的分析。產生該小的間斷的原因是,在計算中,網格尺度是當地自由程的1/5以下,按理一個網格兩側5個網格內的粒子都有可能不經過粒子間碰撞直接到達該網格對熱量交換做出貢獻。但邊界網格內的那個網格在邊界方向只受到臨近一個網格的影響,而損失了一部分粒子對它的影響。比如低溫端右側的第二個網格,它左側只受到第一個網格內進來的粒子的影響,而實際情況應該是有從更遠處的網格中更低溫度的粒子參與能量交換。失去了這些更低溫度粒子的參與,自然要求相鄰網格的更大溫差來彌補。高溫端的情況類似。

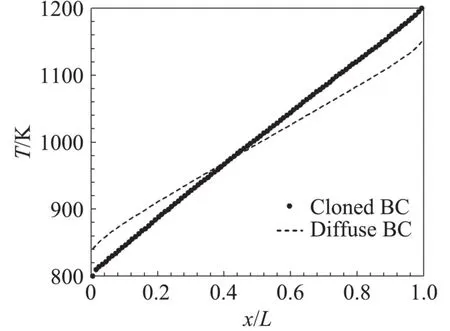
圖5 兩種邊界條件的溫度分布對比(Kn L＝0.2)Fig.5 Comparison of temperature distribution for two different boundary conditions(Kn L＝0.2)

我們還進一步分析了壁面效應對于等效導熱系數計算的影響。為此,在固定ZhT的同時,改變兩壁面間的間距,看大到什么程度后其等效導熱系數不再改變(大小以間距L相當于多少個中心位置的自由分子程數λ0計,即KnL＝λ0/L)。對初始ZhT分別為0.04和0.08的情況采用漫反射邊界和克隆邊界做了兩組算例。圖6給出了所得的導熱系數k的修正值Ak隨ZhT的變化。圖中空心圓和空心三角為完全漫反射邊界計算的結果,并標出了相應的KnL值。紅色實心圓和實心三角為克隆邊界計算的結果。對比發現,漫反射邊界計算所得的Ak隨兩板間距減小而急劇減小,而隆邊界條件計算的Ak的值則幾乎不受兩板間距的影響。對我們所關心的情況,用克隆邊界條件時,計算域最多只要2.5倍的中心位置處的分子自由程就夠了,而對兩端為固壁的情況,則即使ZhT僅為0.04,計算域也要達到10個分子自由程以上才可以。而由于溫度有不能小于零的限制,對兩端固壁情況,有時不可能滿足要求。

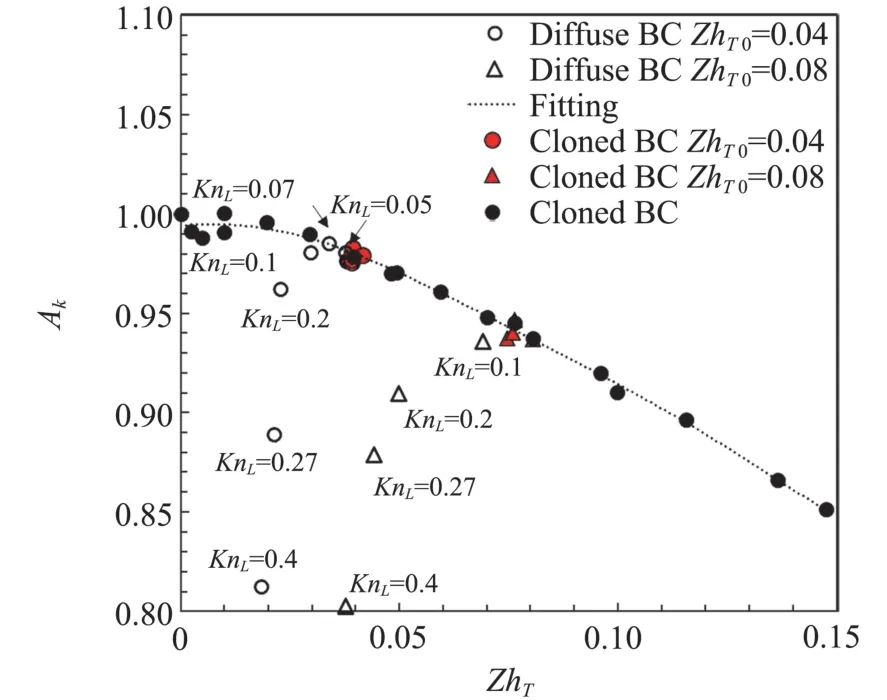
圖6 兩種邊界條件計算的導熱系數修正值對比Fig.6 Correctional coefficients of thermal conductivity calculated by two boundary conditions with parameter Zh T

這部分結果說明:采用壁面漫反射條件在計算域不夠大時不能獲得無量綱參數ZhT和修正系數Ak之間的規律性變化;而克隆邊界可有效消除固壁影響,只需要較小的計算域就能消除壁面對熱流計算產生的影響。對我們研究的情況,只要兩個邊界間距離大于2.5倍中心處的分子自由程,即可獲得相對可靠的結果。

2.3 導熱系數修正曲線A k(Zh T)

我們計算了不同中心點溫度、不同溫度梯度的50個工況,ZhT在[0,0.4]范圍內變化,所得的導熱系數修正曲線如圖7所示。圖中不同顏色符號代表了不同的中心點溫度,從1000 K到2000 K變化,我們可以看到,該曲線不依賴于當地的溫度,只要ZhT相同,所獲得的導熱系數修正值就相同。所有工況的導熱系數修正值Ak隨著ZhT遵循統一的規律,呈單調遞減變化,也就是等效導熱系數比傳統的導熱系數偏小,傅里葉定律計算的熱流值偏大。

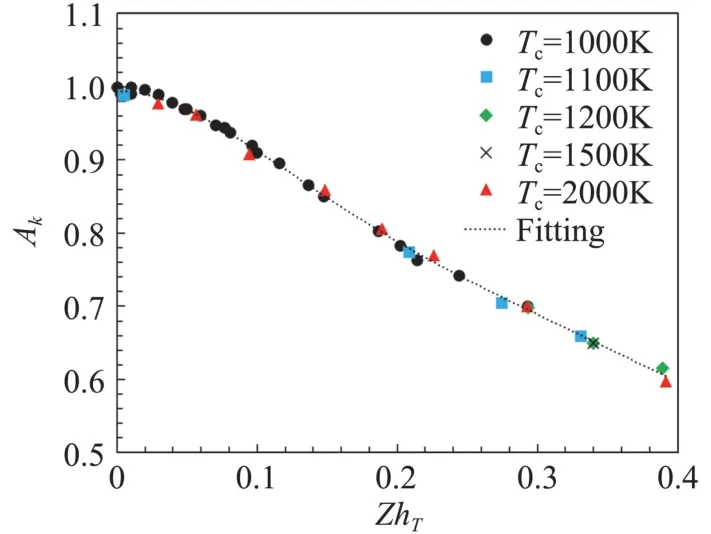
圖7 導熱系數修正值隨無量綱參數Zh T的變化Fig.7 Correctional coefficients of thermal conductivity with parameter Zh T

3 圓柱繞流

為初步驗證上述規律是否可以有效提高對駐點熱流的預測精度,分別采用DSMC和考慮導熱系數修正的CFD模擬了單原子氣體氬氣繞半圓柱的流動。CFD模型的計算框架及計算格式詳見文獻[4,5]。模擬算例為文獻[19]中Kn＝0.05的工況,圓柱半徑為0.1524 m,壁面溫度Tw＝500 K,來流溫度T∞＝200 K,來流氣體的數密度為8.494×1019/m3,來流馬赫數分別為Ma＝10和Ma＝25。

高超聲速繞圓柱流動在駐點附近存在強的溫度梯度,流體沿圓柱表面向后運動時又存在強的剪切。因此,該問題需要同時考慮強剪切和強溫度梯度引起的稀薄氣體效應的影響。在計算中,根據流場當地的參數Zh和ZhT對導熱系數進行了修正。2.3節中獲得了ZhT對導熱系數k的修正值Ak(ZhT),Zh對導熱系數k的修正值Ak(Zh)在文獻[2]中獲得。在此算例中,兩者以加權平均的方式獲得最終的導熱系數的修正值,即:

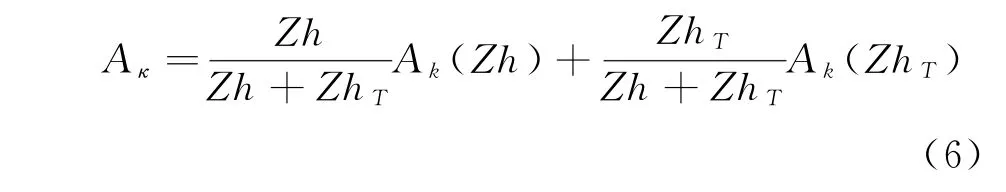
需要說明的是這里作為初步嘗試采用了加權平均的方式考慮參數Zh和ZhT對導熱系數的影響,主要基于流動圖像,認為在駐點附近應是ZhT起主導,沿圓柱表面向后運動的邊界層中應為Zh起主導。更加合理的方式將在今后的工作中探討。

圖8和圖9分別給出了Ma＝10和Ma＝25時圓柱表面熱流系數的計算結果,同時給出了完全漫反射邊界條件計算的DSMC結果,以及使用滑移邊界條件的N-S方程和不使用滑移邊界條件的N-S方程結果。橫坐標?為從駐點開始沿圓柱表面順時針旋轉的角度,縱坐標為無量綱的熱流系數CH＝q/0.。從圖中可以看出,無論是否采用滑移邊界,傳統的N-S方程計算的熱流均高于DSMC結果。而通過本文所建立的導熱系數修正算法對不同馬赫數的圓柱表面熱流,尤其駐點附近熱流預測有了很大的改善。

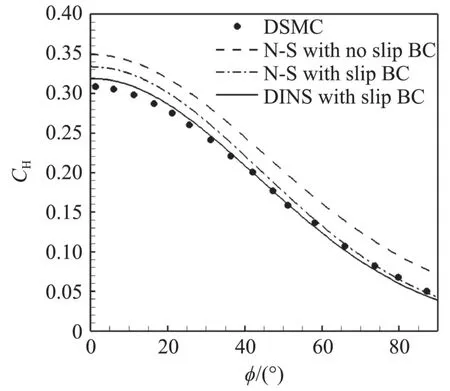
圖8 高超聲速圓柱繞流表面熱流系數(Ma＝10)Fig.8 Surface heating coefficient for hypersonic flow over a cylinder(Ma＝10)

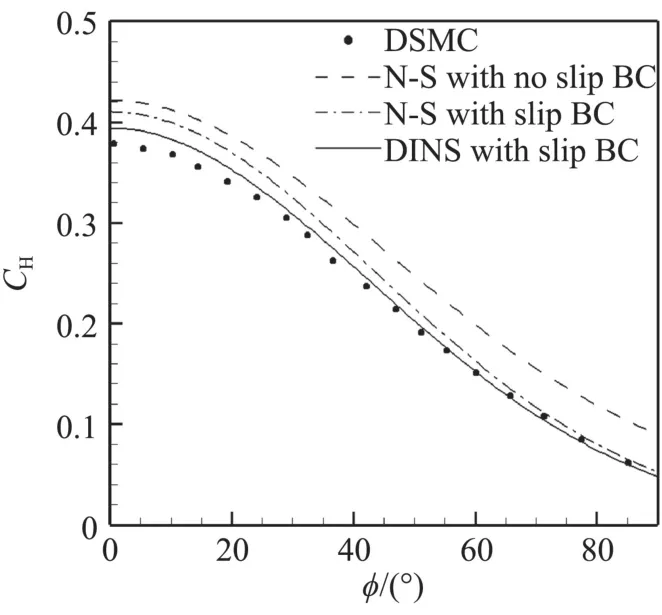
圖9 高超聲速圓柱繞流表面熱流系數(Ma＝25)Fig.9 Surface heating coefficient for hypersonic flow over a cylinder(Ma＝25)

4 結 論

本文以臨近空間高超聲速飛行器氣動熱計算為背景,考慮具有一定稀薄程度的氣體在存在強溫度梯度時熱流的計算。主要獲得以下結論:

1)提出了表征該問題的稀薄效應刻畫參數ZhT;

2)獲得了依賴參數ZhT的導熱系數修正規律;

3)通過導熱系數修正可有效提高高超聲速圓柱繞流壁面熱流的預測精度。

值得說明的是,本文僅考慮了一種簡單的情形,即單原子氣體不存在速度梯度和壓力梯度,僅存在強溫度梯度的情況下對熱流計算的影響。而實際飛行器問題則更為復雜,駐點附近可看作純的導熱問題,但是過了駐點后,法向還存在很大的速度梯度、壓力梯度,并且伴隨高溫的振動能激發,電離離解等效應,需要在今后的研究中逐步分析,以解決真實飛行器流動中的問題。另外,飛行器的壁面條件應如何處理,也是要專門研究的難題。

致謝：感謝周恒院士的指導和通過有啟發性的討論給予的幫助。