凸透鏡成像球差的模擬與測量

余昌愷, 岑 剡

(復旦大學 物理學系，上海 200433)

高性能光學成像系統在軍事、科研、醫學、民用上有大量應用，如導彈的導引頭、光電系統中的熱成像裝置、天文望遠鏡、攝像機鏡頭等[1]. 對幾何成像系統，像差是衡量成像質量的重要指標. 對像差進行測量，可以審核成像系統的設計和制造質量[2]. 在物理教學中，像差相關內容較少，學生對這方面問題缺乏理解. 因而有必要設計合適的像差實驗，加深學生對像差的理解，形成正確的物理圖像.

常見的球差測量方法包括焦面測量法、刀口陰影測量法、哈特曼測量法[3]和剪切干涉法[4-5]等. 焦面測量法是基于2組干涉條紋的重合獲得各環帶光束焦點的位置，在測量時需利用光的干涉現象反復移動CCD，測量過程反復，距離測量精度對結果影響極大. 刀口陰影測量法是利用刀口遮擋光束，基于遮擋位置與陰影圖的關系進行球差測量，其中刀口位置與陰影亮暗交替條紋的寬度間定量關系復雜，不便于數值計算. 哈特曼測量法是二次截面測量法，巧妙地對光線追跡圖進行模擬并進行球差的測量，其操作繁復，測量工作繁重，不利于實驗的開展[1]. 剪切測量法是通過玻璃平行平板形成橫向剪切干涉儀來觀察單薄透鏡形成的準直光束的剪切干涉條紋，并由干涉條紋分布求出對應的幾何像差[4]，其數學計算過程過于復雜繁瑣.

如何在有限時間內完成具有一定測量精度的物理教學實驗具有一定挑戰性，而上文所述的常見測量方法不能滿足實驗教學. 本文基于球差的模型及數值計算方法，利用CCD圖像傳感技術和計算機技術，設計了球差的快速定量測量方法.

1 凸透鏡球差的數值計算

1.1 球差

球面像差簡稱球差，指透鏡成像中入射高度不同的光線不會聚于一點，而分布在透鏡焦點附近區域內的現象，如圖1所示. 球差與透鏡、入射光孔徑角以及入射光與透鏡交點到光軸的距離h相關，可用軸向球差定量描述.

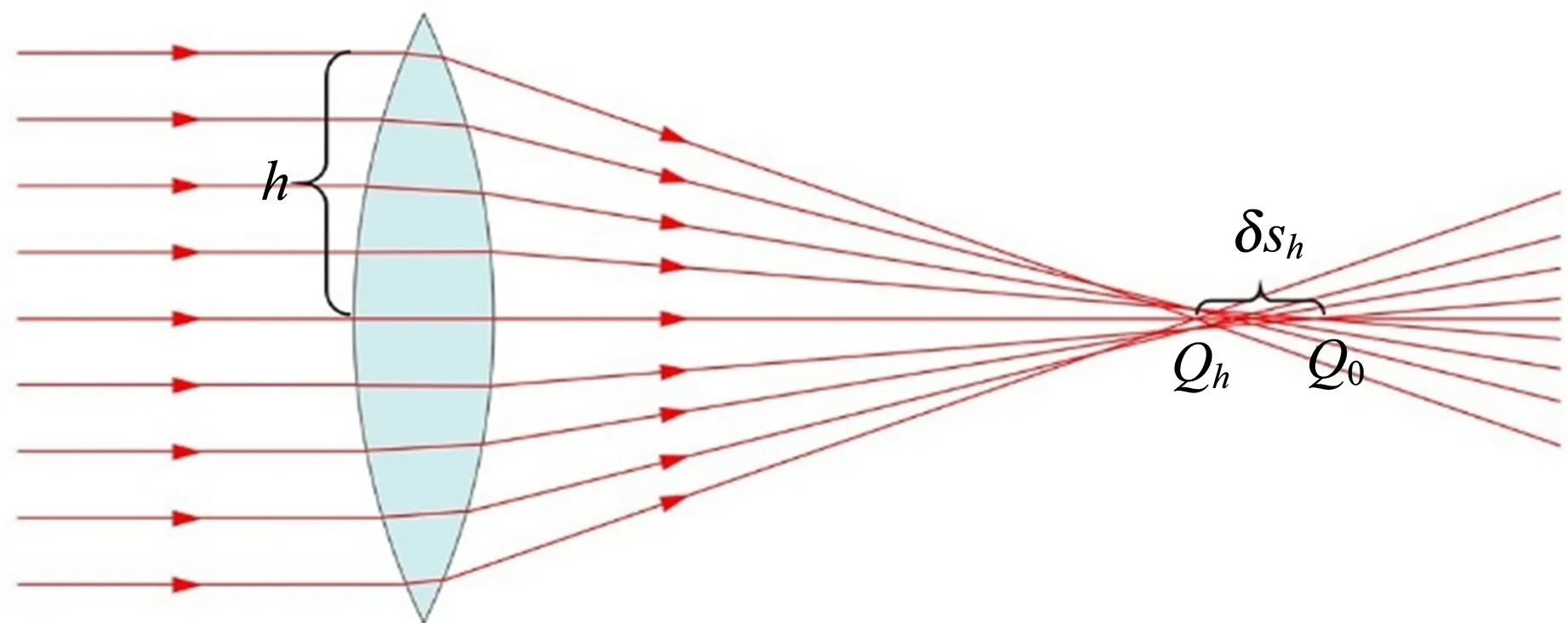
圖1 球差示意圖

設入射光與透鏡的交點到光軸的距離為h，由h入射的光經透鏡會聚于Qh，理想成像點Q0. 軸向球差定義為[6]

δSh=Qh-Q0.

(1)

球差的影響因素較多且解析求解困難. 數值計算軟件的發展為球差計算提供了有效途徑[7].

1.2 球差的數值計算

球差是由于透鏡對傍軸光線與非傍軸光線會聚能力不同造成的. 基于軸向球差的定義，可通過分別計算傍軸及非傍軸光線通過透鏡后的會聚位置得到球差.

1.2.1 單個折射面的折射

考慮一般情況，先分析任意光線經過單個折射球面時的參量變化. 設體系光源為點光源.

對單個折射面，如圖2所示，設折射面曲率半徑r，物空間、像空間折射率分別為n和n′. 設光源到折射面距離l，入射光孔徑角為u，入射角i；像到折射面距離l′，出射光孔徑角為u′，折射角i′. 參量之間的關系為[8]

(2)

初始條件l和u確定后，由方程組(2)可得光線會聚位置l′和孔徑角u′.

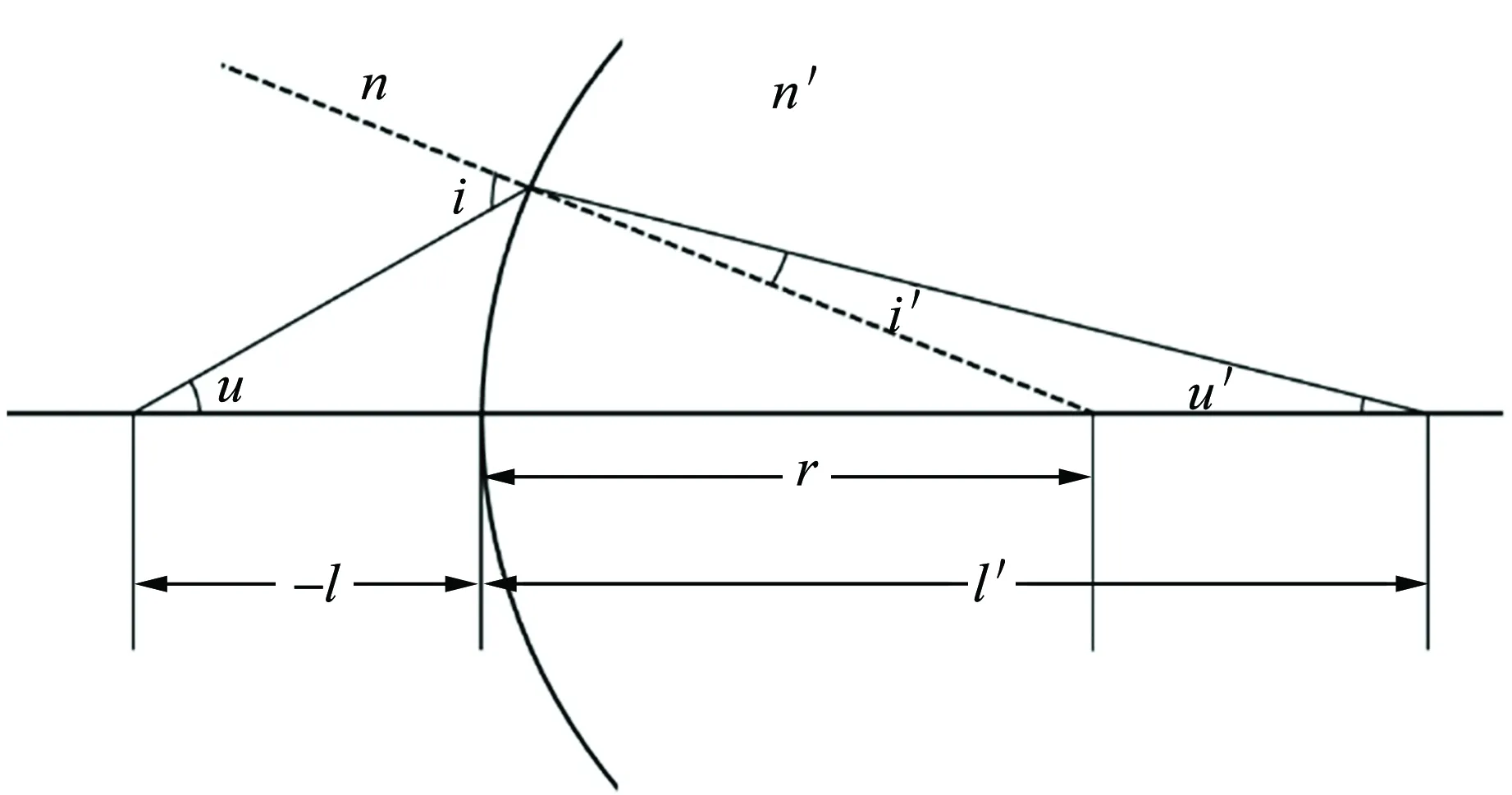
圖2 單折射面光路示意圖

1.2.2 透鏡及透鏡組的折射

對2個及以上折射面的情況，同樣利用方程組(2)進行計算. 對后續的折射面，其初始條件l2及u2為[8]

(3)

其中,l1′及u1′為上一折射面的出射參量，d1為上一折射面與該折射面之間的距離. 將轉換后的初始條件代入式(2)，即可得到光經過該折射面后的出射位置及相應孔徑角. 通過連續的迭代，以上公式即可應用于透鏡組、膠合透鏡等幾何光學成像體系.

1.2.3 基于Matlab的薄透鏡球差數值計算

對于薄透鏡，透鏡參量已知. 將入射光初始條件代入式(3)進行數值計算，即可得到其出射光的會聚位置. 分別計算傍軸光線與非傍軸光線的會聚位置，即可求得透鏡球差.

由上述分析可知，對于單個薄透鏡，出射光的會聚位置L′是入射光位置l、孔徑角u及透鏡參量的函數，即

L′=L′(u,l,r1,r2,n,n′),

(4)

入射光與透鏡的交點到光軸的距離h與孔徑角u的關系為

(5)

則可以將L′改寫為l，h及透鏡參量的函數，即

L′=L′(h,l,r1,r2,n,n′).

(6)

當入射光為平行光時，其會聚位置為光源位于無窮遠處時L′的極限為

(7)

對平行光中的傍軸光線，取Qh的h趨向于零時的極限為

(8)

將初始條件式(6)～(8)，并根據式(1)，即可進行球差的數值計算. 在Matlab中進行球差的數值計算，體系參量如表1所示.

表1 球差數值計算體系參量表

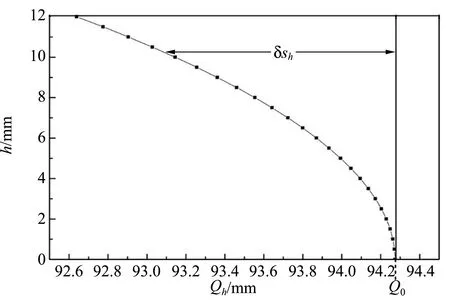
圖3 Matlab球差數值計算

計算結果如圖3所示，可以看到，球差隨著h的增大而增大.

2 球差測量

2.1 球差測量方法

凸透鏡成像的光線追跡如圖4所示. 透鏡位于圖中左側縱軸處. 為了排除孔徑角對球差的影響，實驗使用平行光入射. 要對球差進行測量，只需測量Qh和Q0，二者相減得δsh.

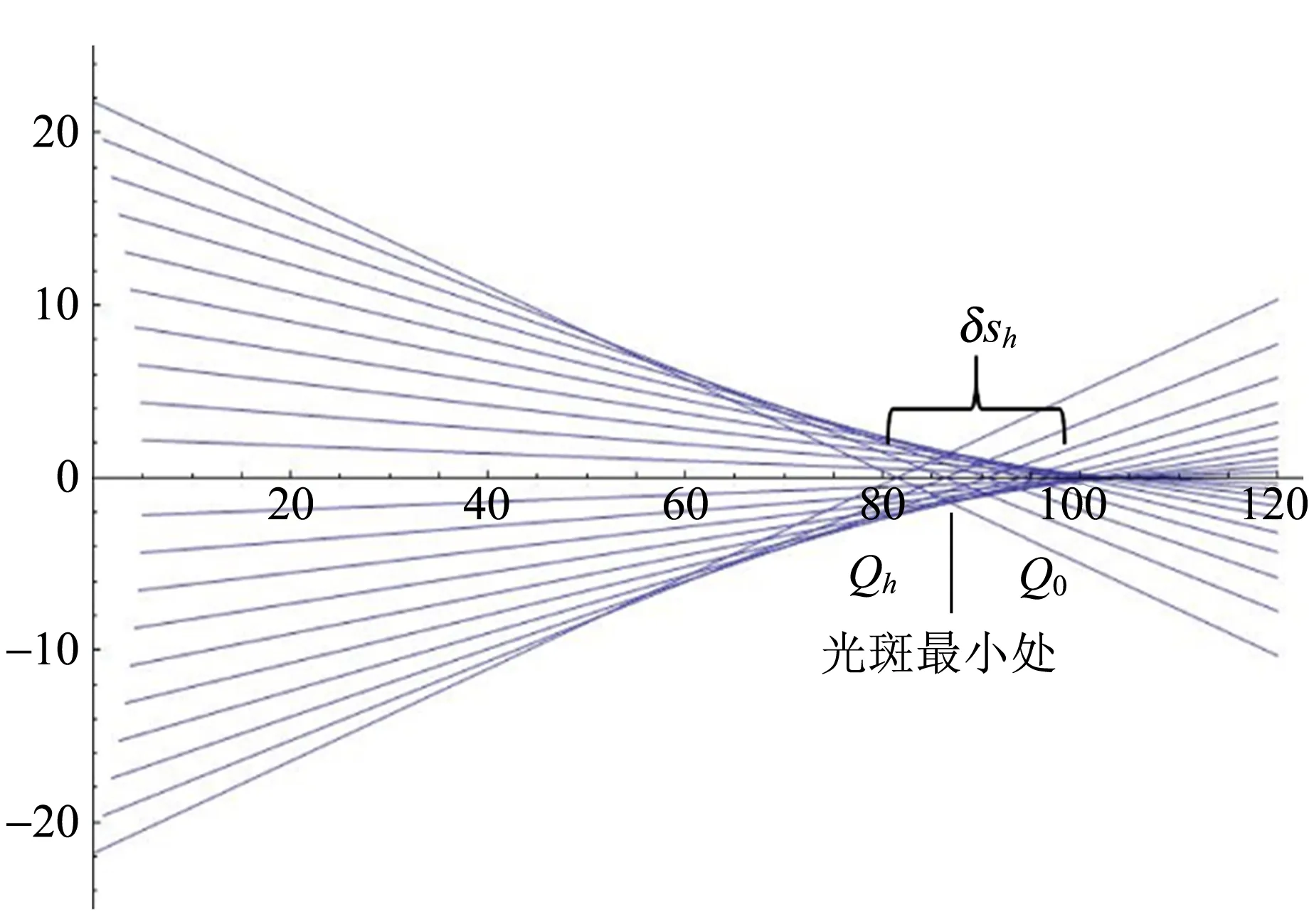
圖4 凸透鏡成像光線追跡圖

2.1.1Qh測量方法

如圖4所示，Qh為透鏡邊緣光線在光軸上的會聚位置. 在靠近焦點的區域內，由于透鏡外側光線的會聚速度較快，與透鏡內側的光線相交，光斑邊緣由內側光線組成；在靠近透鏡的區域內，光斑邊緣仍由透鏡邊緣射出的光線組成，光斑的半徑隨光斑位置線性變化.

基于以上分析，實驗在線性變化區域內，記錄光斑半徑-光斑位置關系，并進行擬合，得到透鏡邊緣光線的直線方程. 利用直線方程算出光與光軸的交點，即可得到Qh. 其中，光斑半徑利用CCD拍攝照片，并利用計算機程序對照片中光斑進行擬合得到.

2.1.2Q0測量方法

如圖4所示，在光斑最小處后，光斑呈現外暗內亮. 隨著觀察位置后移，中心光斑逐漸減小. 在焦點之后，光全部開始發散，中心光斑消失. 反復測量中心光斑最小到消失的臨界位置并取平均，即可得到Q0.

2.2 實驗裝置

實驗裝置如圖5所示. 準直管產生的平行光，經過透鏡會聚在CCD處. CCD連接計算機，利用計算機進行成像的觀察. CCD相機用支座、一維燕尾平移臺及寬滑塊安裝在光具座上. 通過轉動平移臺鼓輪前后移動相機，觀察成像. 平移臺鼓輪最小分度0.01 mm，不確定度限值0.004 mm. CCD傳感器尺寸為1/1.8英寸，分辨率為1 280×1 024.

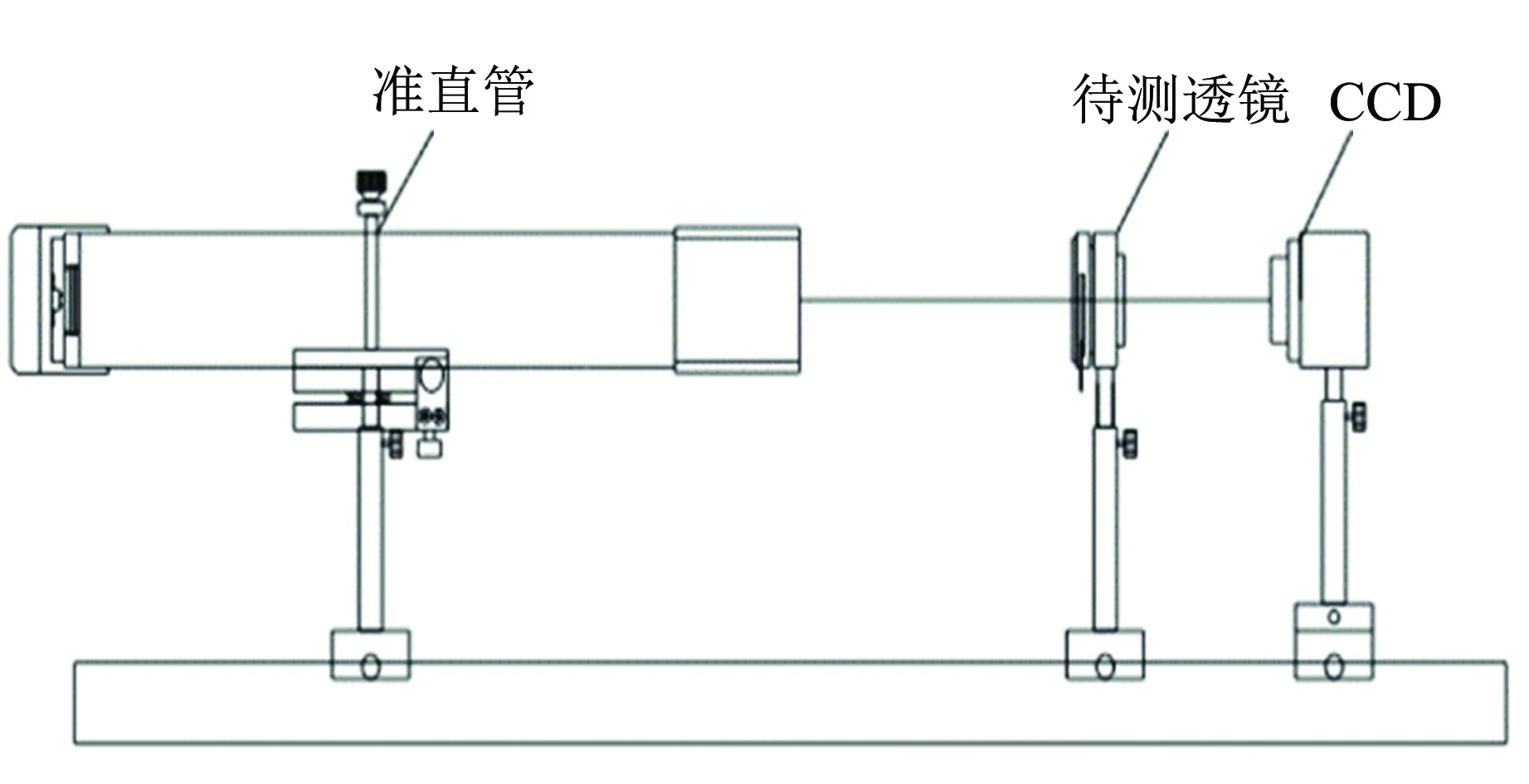
圖5 實驗裝置圖

實驗所用透鏡為BK7玻璃. 準直管紅光波長為630 mm，對應折射率n′=1.515 2.

圖6為準直管的結構原理圖. 準直管由物鏡及置于物鏡焦平面上的帶有小孔的分劃板、光源以及為使分劃板被均勻照亮而設置的毛玻璃組成. 由于分劃板置于物鏡的焦平面上,因此,當光源照亮分劃板后,分劃板上小孔處發出的光經過透鏡后成為平行光. 這樣,對觀察者來說,分劃板又相當于無限遠距離的目標.

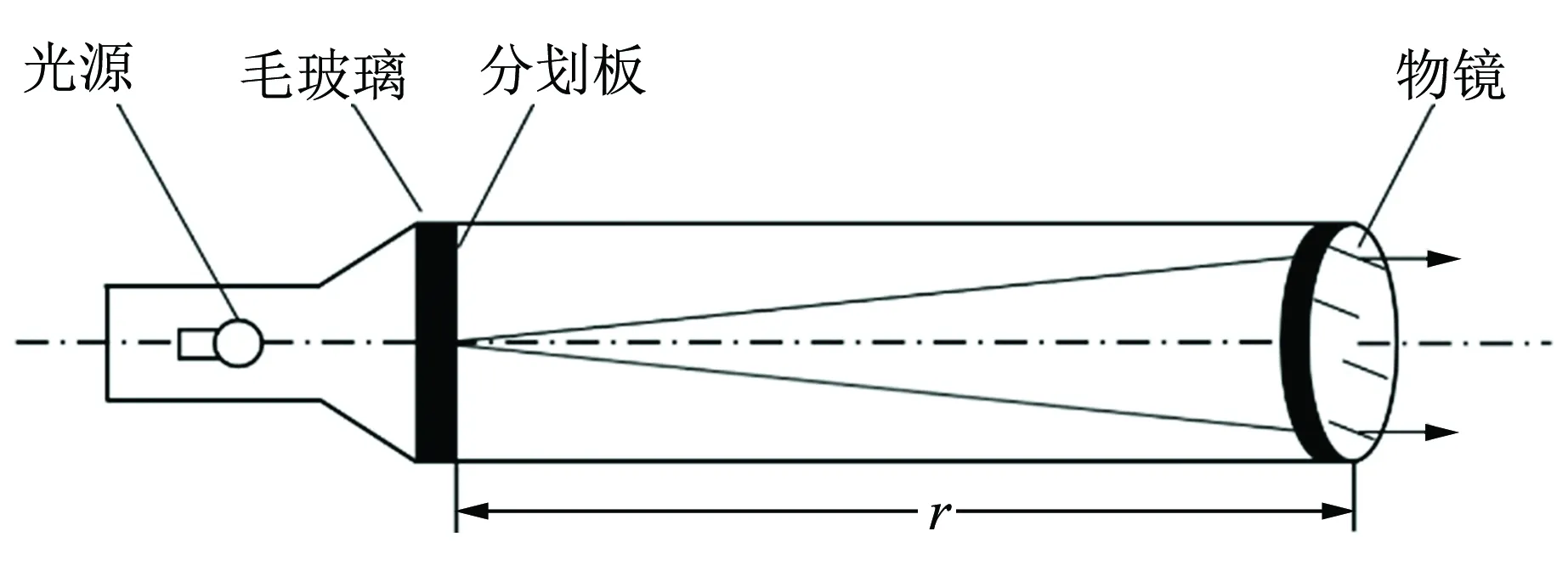
圖6 準直管結構原理圖

3 實驗結果及討論

3.1 軸向球差測量結果

用上述方法對軸向球差進行多次測量，記錄Qh和Q0測量值，求出軸向球差并取平均，實驗結果如表2所示. 計算得球差δsh=(1.52±0.07) mm. 在Matlab中用上述原理進行計算，得球差數值計算結果為δsh=1.55 mm. 實驗測量值相對偏差為2%. 計算所得理論值在實驗不確定度范圍內，在目前測量條件下，二者互相吻合，實驗誤差較小.

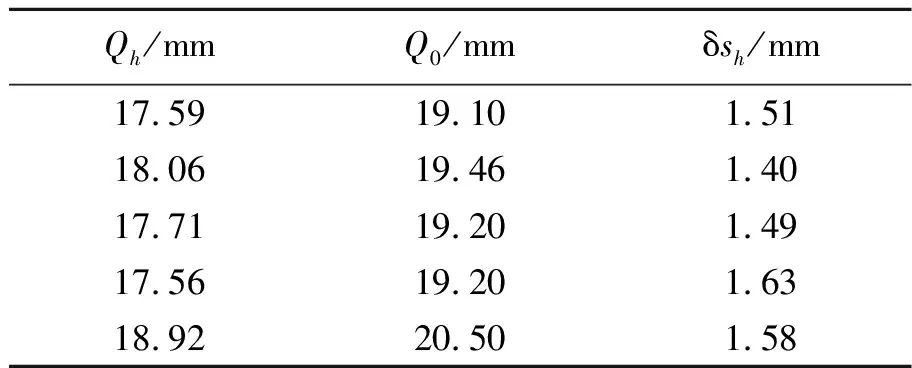
表2 球差測量實驗數據表

3.2 初級球差的光斑特征

球差現象對凸透鏡成像的影響是實驗設計的基礎與核心. 對球差現象的觀察能有力促進學生對球差的理解. 在一般的凸透鏡成像實驗中，由于光源亮度過大，肉眼無法直接觀察到光斑內部的光強分布. 本實驗通過減弱光源強度并結合CCD圖像傳感技術，可在完成具有一定精度測量的同時直觀地展示初級球差的光斑特征，便于學生形成物理圖像.

球差對光斑的影響主要體現為：光無法會聚至一點并形成具有一定面積的光斑；光斑半徑與位置的非線性關系；光斑內部的光強分布及最小光斑前后光強分布的不對稱性.

在理想情況下，入射平行光被透鏡會聚于焦點并發散. 會聚形成的光斑亮度均勻且關于焦點對稱. 在實際情況下，非傍軸光線被會聚于透鏡焦點前某處；而傍軸光線被會聚于焦點處. 由于會聚位置分布在焦點附近的一片區域內.

如圖7所示，A區域光線分布相對均勻，光斑亮度相對均勻；B區域光線外側密集，內部稀疏，光斑由外部亮圓環與內部較暗的圓組成；C區域光線內部密集外側稀疏，光斑內亮外暗，分為內部較亮的圓與外部較暗的圓環；D區域光線發散，光斑亮度從內向外遞減.

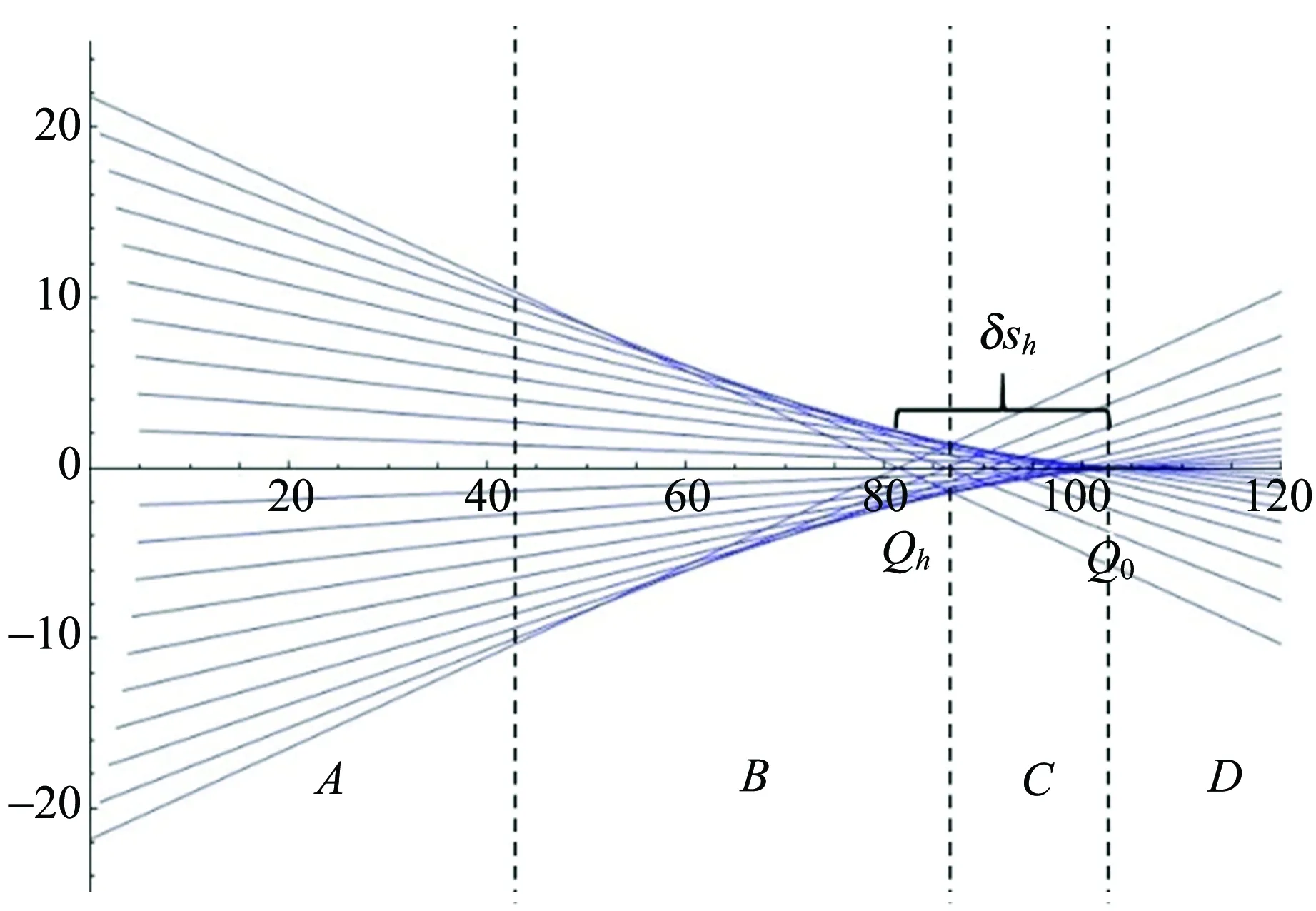
圖7 光線追跡圖及其分區

在距離透鏡不同位置利用CCD拍照，圖像及在追跡圖中的對應區域如圖8所示. 圖8(a)中光斑亮度相對均勻；圖8(b)中光斑外亮內暗；圖8(c)中光斑內亮外暗；圖8(d)中光線發散，亮度從內向外遞減. 實驗現象符合預期.

圖8 凸透鏡成像實拍圖

3.3 光斑半徑-位置關系

理想透鏡中，光斑半徑與位置呈線性關系. 實際情況中，如圖7所示，由于透鏡邊緣光線會聚速度快，在B區與透鏡內側光線相交，光斑半徑與位置呈非線性關系. 實驗測得二者關系如圖9所示.

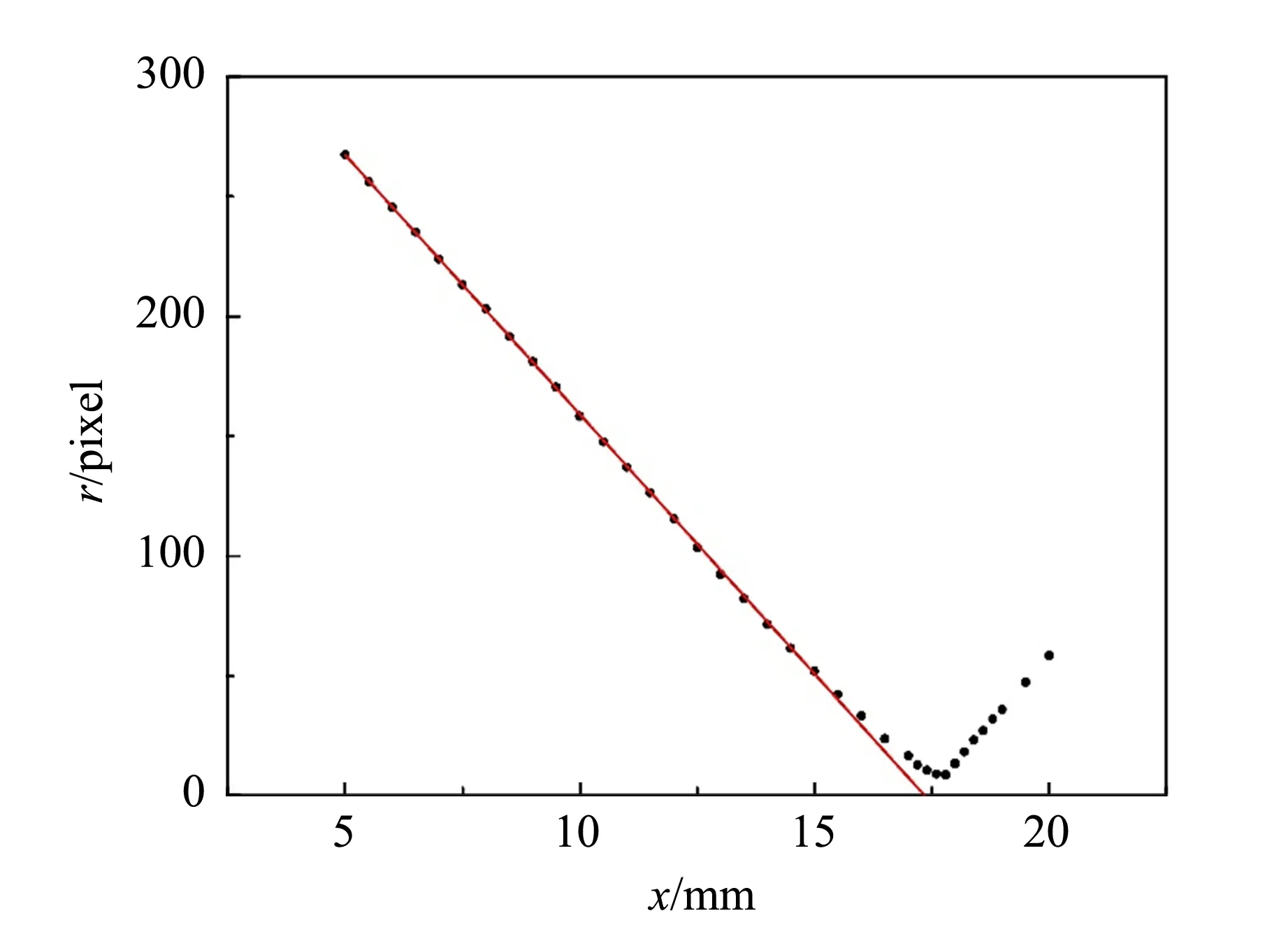
圖9 光斑半徑-位置關系圖

由圖9可知，在光斑最小處前，光斑半徑隨位置先線性減小，隨后曲線斜率逐漸減小，二者呈非線性關系；光斑最小處后，光斑半徑隨位置線性增大. 因此進行Qh測量時，光斑最小處前方直線的測量應選取距離光斑最小處前較遠位置，否則測得球差具有一定誤差.

3.4 曝光時間的影響

在CCD圖像的獲取中，曝光時間是影響圖像質量的重要因素. 如圖10所示，隨著曝光時間增加，光斑細節更加清晰. 另一方面曝光時間增加導致過曝光的出現且噪聲、環境光的影響增大. 過曝光區域面積隨曝光時間增大而增大. 觀察及拍照時應選擇合適的曝光時間以在背景光、噪聲較小的前提下，避免圖像細節的丟失.

(a)40 ms (b)60 ms (c)80 ms圖10 不同曝光時間下的B區光斑

在Q0測量中，圖像的中心亮斑觀察與曝光時間密切相關. 若曝光時間過長，Q0前后一段區域內圖像均有中心亮斑，且亮斑較大，不利于Q0測量；另一方面，從Qh處至Q0處，光軸上的光通量逐漸減小，若曝光時間過短，或觀察不到中心亮斑，導致Q0測量值偏小.

3.5 Qh測量誤差及其改進

實驗不確定度主要來源于Qh的測量誤差，Qh貢獻了90%以上的不確定度.Qh的測量精度受CCD圖像質量及圓識別算法的限制.

實驗采取霍夫變換法對CCD拍攝圖像進行圓識別. 圓形識別的精確度受光斑對比度、邊緣連續度、噪聲等的影響[9]. 如上文所述，Qh的測量需要A區域光斑半徑的測量. 實驗所取測量位置的光斑半徑為光斑最小半徑的20～30倍，因而光斑光強、邊緣亮度梯度較小. 實驗采取了改變圖像整體亮度、對比度的方法增大光斑亮度，但由于原圖像亮度較低，環境光及噪聲的相對強度較大，亮度提升的同時噪聲強度也得到了增強，光斑半徑測量具有一定誤差.

實驗改進應主要考慮圖像質量的提升以及圖像預處理方法的改進. 圖像質量上，可通過提升光源亮度、減少背景光的辦法提升原圖像中的光斑對比度. 圖像預處理方面，考慮通過改進預處理方法，減少背景光、噪聲對圓識別的影響.

4 結 論

根據凸透鏡成像的理論模型，設計了簡單的球差定量測量方法. 該方法基于軸向球差的定義，通過分別測量非傍軸光線以及傍軸光線的會聚位置測得透鏡球差，相比于其他測量方法更易于理解，測量過程也更加簡便. 根據模型計算結果，推測凸透鏡成像過程中光斑呈現從亮度均勻到外亮內暗，再到外暗內亮直至最后完全發散的現象. 利用CCD圖像傳感技術觀察光斑內部光強分布，實驗結果符合預期. 實驗測得在平行光入射條件下，待測透鏡軸向球差δsh=(1.52±0.07) mm，相對誤差2%.