基于隸屬度和LMK-ELM的航空電子部件診斷方法

朱敏，許愛強，李睿峰，戴金玲

海軍航空大學，煙臺 264001

模塊級故障診斷屬于航空裝備三級維修體系中的中繼級維修范疇，是提升航空保障能力的關鍵環節。航空電子設備各模塊間交聯關系復雜[1-3]，難以對各故障建立嚴格的數學模型，這對故障診斷帶來了極大的挑戰[4-5]。

基于數據驅動的方法為解決上述問題提供了良好的思路。其中，深度學習與基于核方法的學習算法在航空電子部件的故障診斷中得到了最廣泛的關注。前者主要適用于故障樣本充足、計算資源豐富的情況，因此應用范圍較為狹小，在電路元件級診斷中較為常見，文獻[6-7]用深度置信網絡(DBN)自動提取模擬電路的抽象故障特征，極大地提高了診斷正確率；考慮到神經網絡訓練時間長以及固有的人為經驗依賴性，文獻[8]結合數據壓縮和自編碼技術，提出了一種基于改進人工神經網絡的航天器電信號分類方法。后者在小樣本條件下尤為適用[9]，在文獻[10-11]中，支持向量機(SVM)與核極限學習機(KELM)分別被運用于電子系統的故障診斷，展現了較強的統計學習能力。此外，從診斷方法的角度看，為使航空電子設備的診斷結論更加可靠，將多個分類器的結果進行信息融合是另一個重要的研究方向[12]；從診斷對象的角度看，作為航空電子設備在服役中后期的主要故障類型，間歇故障的診斷正受到越來越多的關注，將成為復雜電子設備故障診斷的新方向[13]；從診斷的基礎看，當前航空電子設備很少考慮故障診斷的測試需求，直接導致特征參數獲取困難，因此，測試性設計技術也依然是研究的重點[14]。

實際應用中，航空電子部件的樣本規模一般很小[11]，因此，基于核方法的學習算法更有前景。在該類方法中，核函數及其參數的選取將嚴重制約方法的性能[15-16]。大量研究表明，多核學習(Multiple Kernel Learning, MKL)可增強決策函數的可解釋性，且比單核模型具備更優的性能[17-18]。文獻[19-20]分別在模擬電路、局域網的故障診斷中嘗試運用MKL，在多種復雜故障情形下驗證了MKL對提升診斷精度的有效性。文獻[21]提出了一種更有效的MKL方法，稱作SimpleMKL，通過簡單的子梯度下降方法求解MKL問題，提高了MKL的實用性。但在MKL的框架里，基核權重被不加判別地應用于整個輸入空間，忽視了基核在不同樣本上可用性的差異。針對該問題，局部算法被引入到MKL中，稱之為局部多核學習(Localized MKL，LMKL)。

近年來，國內外學者對LMKL進行了廣泛的研究，大致可分為兩類。一類為每一個樣本學習一組獨立的基核權重，稱之為面向樣本的LMKL(Sample-based Localized MKL，S-LMKL)模型[22-23]。針對S-LMKL中局部權重的優化形式二次非凸的問題，文獻[24]中G?nen和Alpaydin通過一系列參數化的門模型(Gating Model)去局部地擬合核參數；文獻[25]則著重研究了SVM分類框架下，對基核權重施加不同的范數約束對LMKL的影響。另一類是由Yang等[26]最初提出的基于分組的LMKL(Group-based Localized MKL，G-LMKL)模型，該方法首先根據樣本相似性進行聚類，再為每個聚類學習一組基核權重，繼承了S-LMKL的局部特征自適應表達能力，還有效約減了計算量，避免了過擬合。基于文獻[26]的思想，文獻[27]將聚類過程嵌入LMKL的訓練中，提出了基于動態聚類的G-LMKL模型；文獻[11]則引入近鄰傳播聚類來挖掘局部特征信息，由于事先不需指定聚類數目，使得G-LMKL對于不同規模的樣本均具有較好的實用性。

G-LMKL克服了S-LMKL面臨的主要風險，并且可以通過控制聚類數量來控制計算復雜性，更具靈活性。然而，G-LMKL中簡單的“硬聚類”并不足以有效描述樣本間的多樣性，在同一聚類的內部基核的可用性顯然也存在差異。出于這樣的考慮，針對航空電子設備故障樣本的采集困難性、分布復雜性以及本身固有的不確定性，提出一種小樣本條件下融合隸屬度信息的局部多核超限學習機模型(Fuzzy Clustering Localized Multi-Kernel Extreme Learning Machine，FC-LMKELM)，其主要貢獻在于：

1) 不同于現有的基于SVM的G-LMKL，受2015年提出的多核超限學習機(MK-ELM)[28]和文獻[11]啟發，本文將G-LMKL與ELM結合，從理論上給出了G-LMK-ELM的形式化表達。

2) 不同于已有的基于“硬聚類”的G-LMKL，基于模糊C均值聚類結果，本文的核權重將由樣本落入各聚類的概率以及為每個聚類分配的核權重共同決定。在繼承一般G-LMKL算法局部特征自適應能力和計算復雜性約減能力的同時，還進一步挖掘類內多樣性，有利于提高診斷精度。

3) 針對局部權重優化形式的二次非凸問題，通過剖析G-LMK-ELM的初始優化問題及其對偶優化問題之間的關系，搭建了面向初始-對偶混合優化問題的參數三階段交替更新策略。

1 問題描述

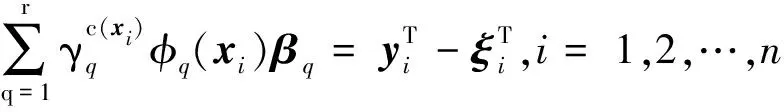
(1)

式中：βq∈R|φq(·)|×m為基于第q個基核的輸出權重；|φq(·)|為第q個基核誘導的特征空間維數，m為類別數量；yi=[yi1,yi2,…,yim]T和ξi=[ξi1,ξi2,…,ξim]T分別為與xi對應的理想輸出向量和誤差向量；C為正則化因子。

在該問題的Lagrange函數中分別對βq和ξi求偏導，并令結果等于0，可以進一步獲得其對偶優化形式，即

(2)

式中：αi為Lagrange乘子，對應于ELM的模型參數，并且有αi=[αi1,αi2,…,αim]T，α=[α1,α2,…,αn]T。

求解上述對偶優化問題，得到以下決策函數

(3)

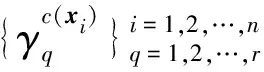
2 基于隸屬度的G-LMK-ELM診斷模型

2.1 基于模糊C均值聚類的樣本空間劃分

本節運用模糊C均值聚類方法(FCM)[29]對數據集進行模糊劃分，進而達到挖掘樣本局部分布特征的目的。不同于硬聚類方法，模糊C均值聚類可以獲取每個故障樣本對于各個聚類的隸屬度，將該隸屬度信息作為先驗知識融入G-LMK-ELM的局部核權重的優化中，有利于增強診斷模型的解釋性，提高其診斷精度。

在FCM中，對樣本的模糊劃分可以表示成一個隸屬度矩陣U=[uij](1≤i≤n,1≤j≤C)，且U滿足:

(4)

式中：μij為第i個數據關于第j個聚類的隸屬度，uij越大，則第i個數據落入第j個聚類的概率越大。FCM算法的具體實施流程描述如下：

步驟2更新聚類中心

步驟3更新隸屬度矩陣

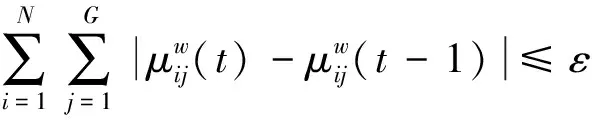
2.2 基于隸屬度的FC-LMKELM診斷模型優化

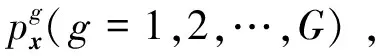
(5)

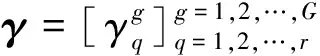
(6)

式(5)和式(6)對應的基于隸屬度信息的FC-LMKL-ELM優化問題可以等效為式(7)所示的初始-對偶混合優化問題

(7)

證明：

步驟1由表達式(5)到表達式(7)

初始優化問題(5)對應的Lagrange函數為

在Lagrange函數中對ξi求偏導，并令結果等于0，有

將該結果代入Lagrange函數中，得到式(7)。

步驟2由表達式(7)到表達式(6)

將表達式(7)重新寫為

(8)

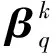
(9)

將式(9)代入式(7)中，整理后可式(6)。

證畢。

2.3 FC-LMKELM的模型優化

為了求解融合隸屬度的FC-LMKELM模型，針對式(7)定義的優化問題，提出一種3階段的參數交替優化策略。

1) 固定γ，優化α

(10)

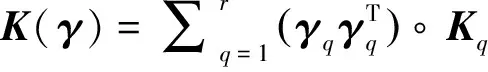
圖1 增廣矩陣K′
Fig.1 Augmentation matrixK′

對式(10)的α′求偏導，并令結果等于0，可得

α′=(K′+I″/C)-1y′

(11)

2) 給定α、γ，計算βq和fq(xi)

(12)

不妨用fq(·)表示第q個基核導出的子分類器的輸出函數，則樣本xi基于fq(·)的輸出向量為

(13)

3) 固定α、fq(xi)，更新γ

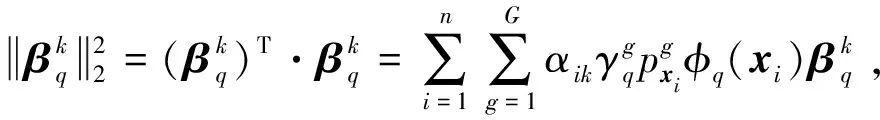
(14)

種不同的局部權重更新方式。

1)l1-范數約束

基于直流線路參數的50Hz諧波放大評估方法//李曉華,吳立珠,丁曉兵,張冬怡,吳嘉琪,蔡澤祥//(6):146

2)lp-范數約束

式(14)在lp-范數約束下的Lagrange函數表示為

(15)

(16)

聯合lp-范數約束條件和式(16)，可得

(17)

特別地，當p=2時，有

(18)

2.4 診斷決策

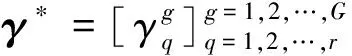
(19)

決策模型的圖形解釋如圖2所示。

在融合隸屬度的FC-LMKELM模型中，不妨設測試樣本的模型輸出f(z)={f(1)(z),f(2)(z),…,f(m)(z)}，其中，f(l)(z)對應于第l個節點的輸出值，則z的故障模式判定為

(20)

融合隸屬度的FC-MKELM模型整體框架總結如圖3所示。

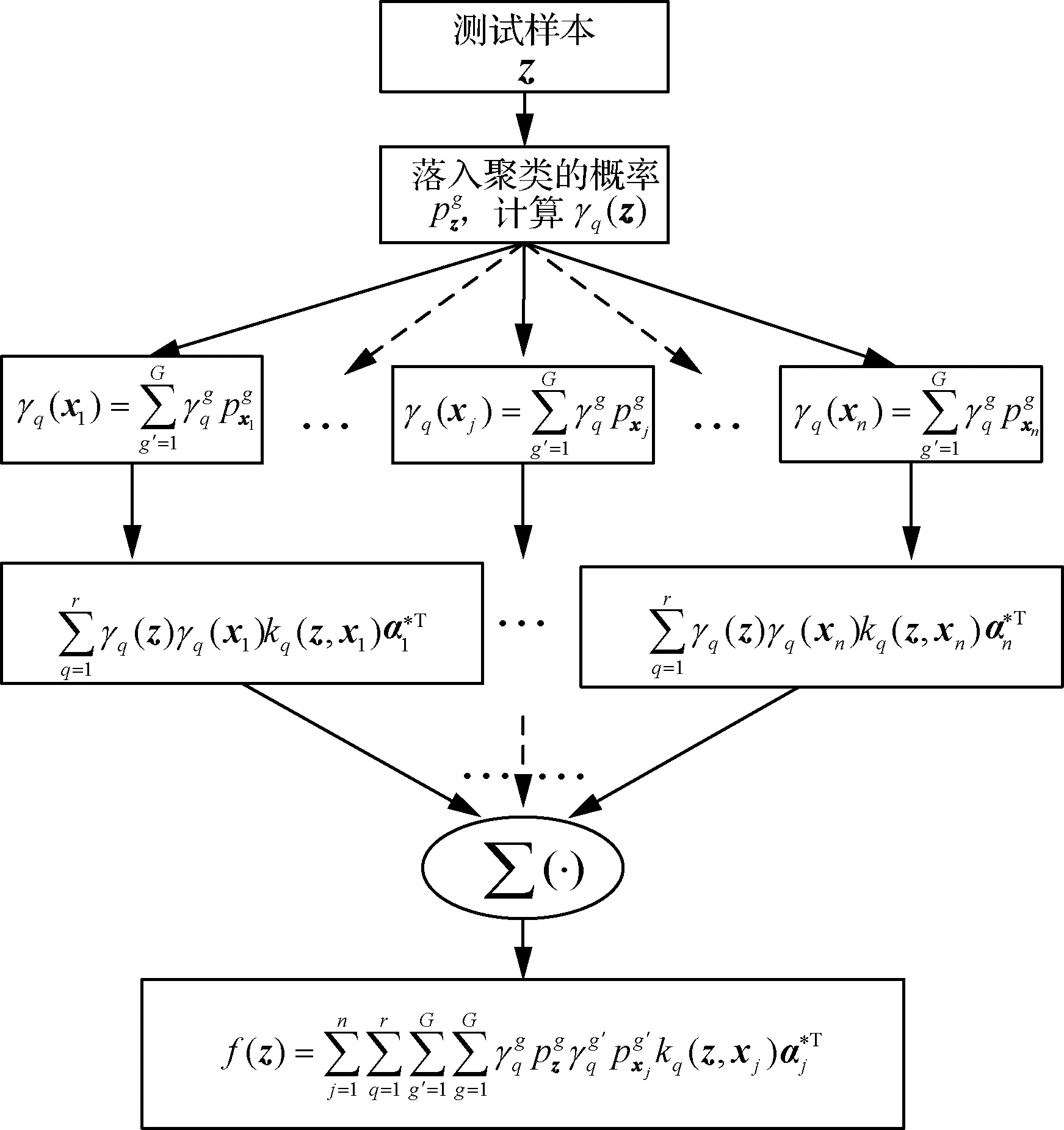
圖2 FC-LMKELM的決策模型
Fig.2 Decision-making model of FC-LMKELM

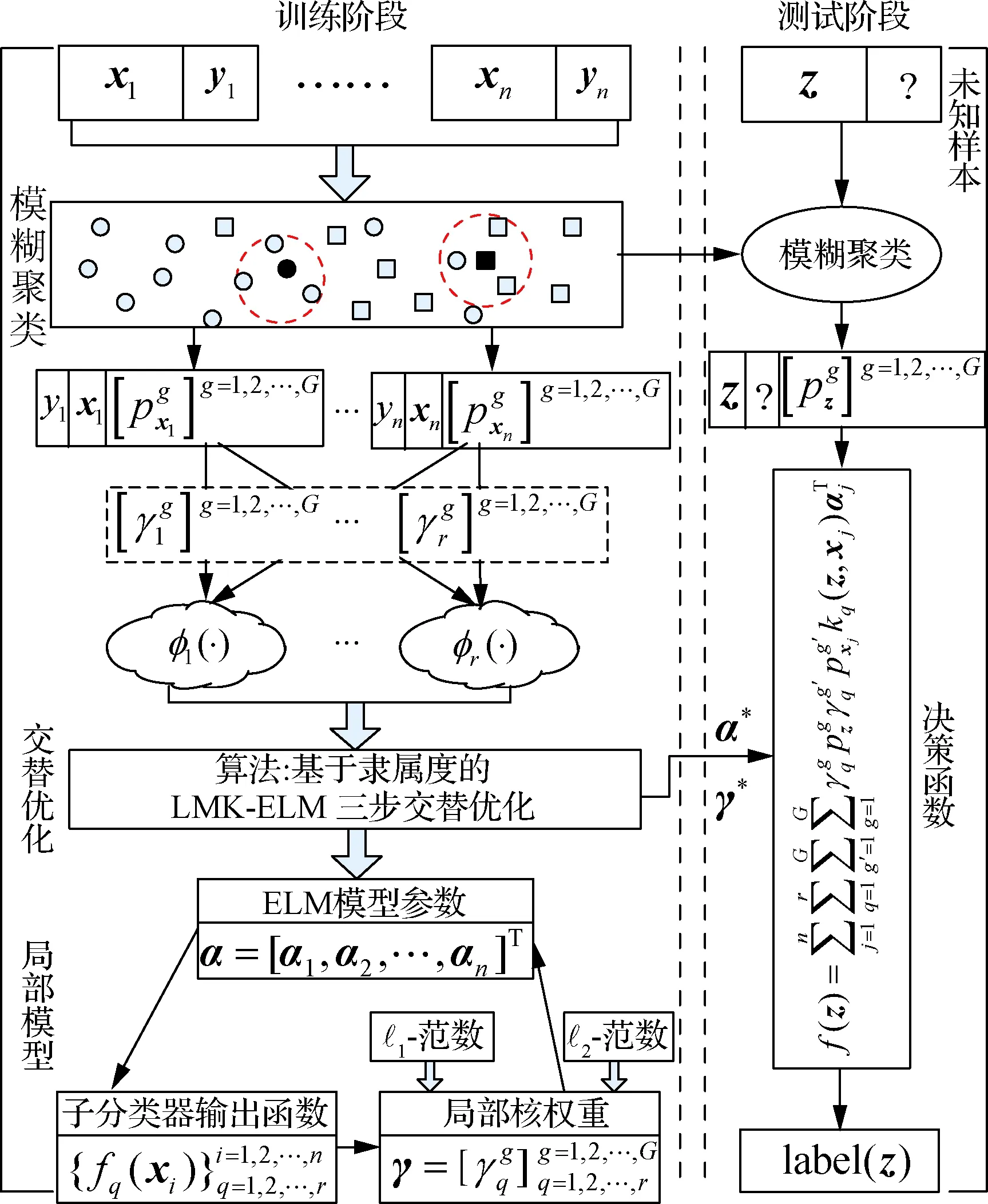
圖3 FC-MKELM模型的流程圖
Fig.3 Flowchart of FC-MKELM model

3 方法流程

為方便表示，不妨將采用l1-范數和l2-范數約束時的FC-LMKELM分別記為l1-FC-LMKELM和l2-FC-LMKELM。根據圖4將所提方法的實施流程總結如下：

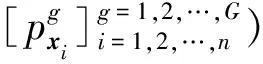
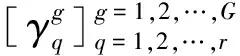
步驟4通過式(13)計算fq(xi)。

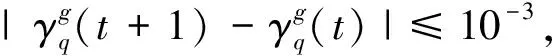
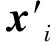
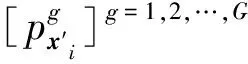
4 實驗分析

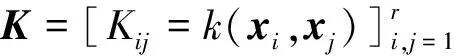
所有算法均在MATLAB 2018a上運行，實驗電腦配置為：Windows 7操作系統，Inter Core i7-4770 CPU，3.4 GHz主頻和8 GB RAM。

4.1 方法有效性驗證

本節通過人造數據集Gauss4證明FC-LMKELM的有效性。由于Gauss4具有明顯的類內局部結構，因此常用其進行局部算法的性能驗證[11,24]。該數據集包含2種類別，每個類別服從2個不同的高斯分布，每個分布產生300個樣本，共1 200個樣本。與文獻[11,24]一致，每種分布的先驗概率、均值、協方差為

ρ11=0.25，ρ12=0.25，ρ21=0.25，ρ22=0.25

實驗共進行20次，每次隨機選擇600個樣本用于訓練，400個樣本用于測試，設置所提方法的聚類數量為4。將所提方法與SimpleMKL[21]、M1-LCMKELM[11]、M2-LCMKELM[11]、S-LMKL-softmax[24]、S-LMKL-sigmoid[24]比較。參考文獻[11,24]中的配置，上述所有方法均以線性核、參數是2的多項式核、參數是1的高斯核作為基核；F1分數是統計學中衡量二分類模型精確度的重要指標[30]，本節將之與分類準確率以及文獻[31]中的G-mean作為評價分類性能的3大指標，其值以“均值±標準差”的形式記錄于表1中。

由表1可知，與其他方法相比，在l1-范數和l2-范數約束下，FC-LMKELM可以實現最優的分類性能。其原因在于：

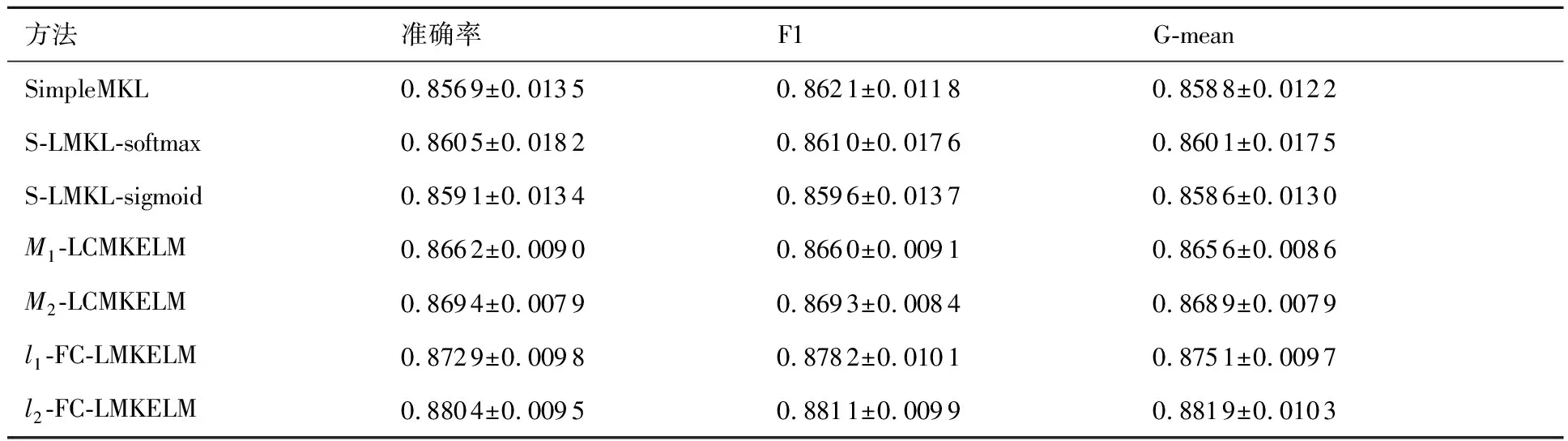
表1 實驗1中各指標值Table 1 Index values in experiment 1

1) SimpleMKL沒有考慮樣本的局部特征信息，因此在所有方法中，其分類性能最差。

2) 與2種常見的S-LMKL方法相比，LCMKELM和FC-LMKELM將基核權重擬合到樣本所屬聚類而非每個樣本上，一定程度上抑制了過學習問題，分類精度得以提升；與2種基于硬聚類的LCMKELM方法相比，隸屬度信息的融入使FC-LMKELM得以有效描述聚類內部樣本間的多樣性，因此，即便與診斷性能更佳的M2-LCMKELM相比，在不同范數約束下，診斷精度也分別提升了0.35%和1.10%。

為更直觀地展現FC-LMKELM相較于其他方法的優勢，選取l2-FC-LMKELM、SimpleMKL、S-LMKL-softmax與M1-LCMKELM的受試者工作特征曲線(ROC)繪制于圖4中。由圖4可知，l2-FC-LMKELM的曲線下方面積(AUC)依次大于M1-LCMKELM、S-LMKL-softmax和SimpleMKL，這進一步驗證了所提方法的性能。

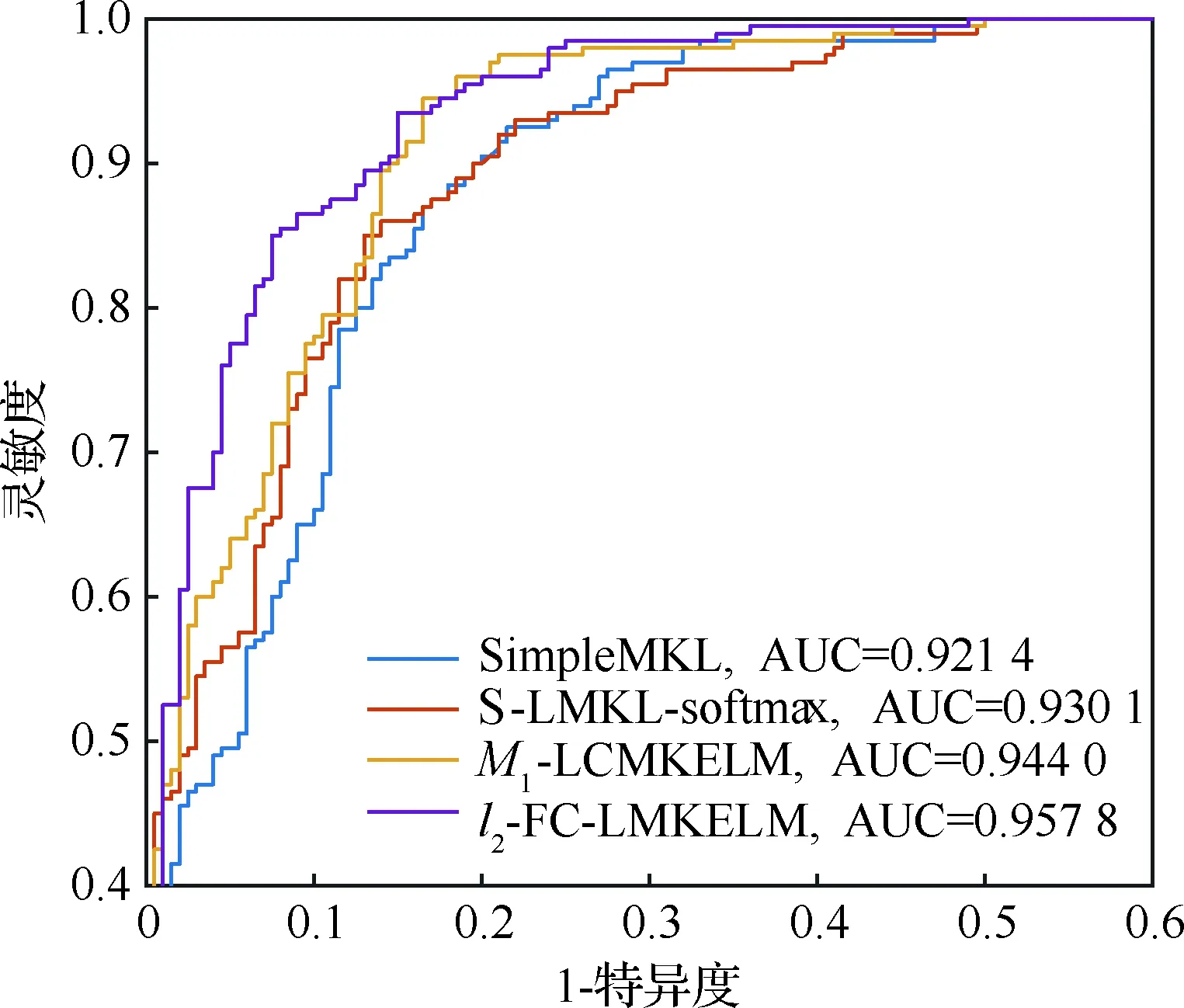
圖4 4種方法的ROC曲線
Fig.4 ROC curves of 4 methods

為說明聚類數量對算法精度的影響，隨機選擇600個樣本用于訓練，400個樣本用于測試，設置不同的聚類數量后，其測試結果如表2所示。

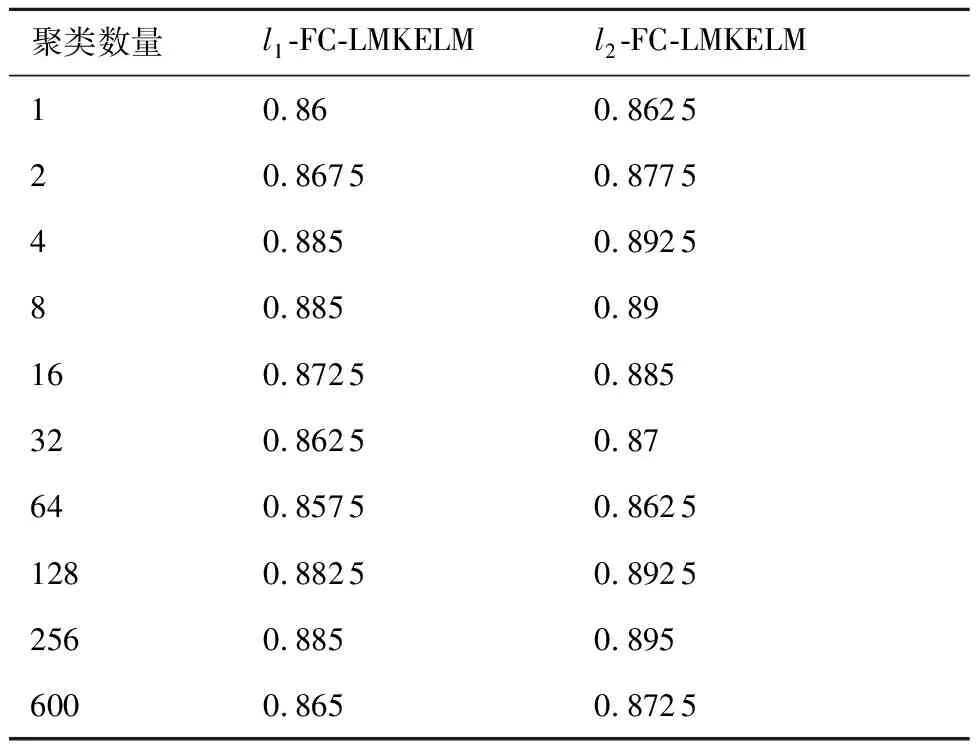
表2 不同聚類數目時的分類準確率

由表2可知：當聚類數量為1時，診斷精度處于較低水平；隨著聚類數量增加，模型診斷精度出現不同程度的提高，但最佳的聚類數量與輸入空間的局部結構有關，并無明確的規律可循，當聚類數量取值不當時，測試精度甚至會出現下降；當聚類數量增加到訓練樣本數量時，本文方法演變為S-LMKL-ELM，泛化性能有所降低。

4.2 某型機前端接收機故障診斷實例

某型機前端接收機組成如圖5所示，本節以其為例，驗證FC-LMKELM的有效性。自動測試系統(ATS)對其進行12項測試：5個頻點的靈敏度、動態范圍，以及兩項射頻增益。用F0、F1、F2、F3分別表示正常模式、放大單元故障、微波單元1故障和微波單元2故障。ATS對每種模式采集48組樣本，共得到192組樣本，將之均分后形成訓練集和測試集。基于廠家維護保養手冊中的測量方法，利用ATS的標準信號源、功率計和頻譜儀對每種模式采集48組樣本，共獲得特征數為12、樣本數為192的原始數據集，對該數據集按特征進行Z-score標準化預處理，然后將之均分為訓練集和測試集。運用t分布隨機鄰域嵌入(t-SNE)算法[32]將訓練集的96個樣本降維到三維空間中，如圖6所示。顯然，不同故障模式的樣本間重疊嚴重，同一故障模式的樣本分布也并不集中，這對分類算法性能提出了較高的要求。

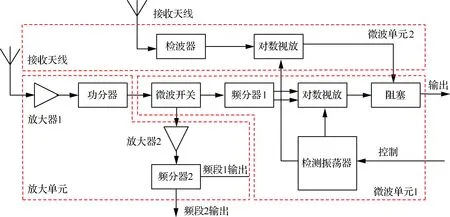
圖5 前端接收機
Fig.5 Front-end receiver

圖6 訓練集的三維可視化圖
Fig.6 3-D visualization of training set

基于該訓練集，以線性核、參數為2的多項式核、參數分別為[2,10,20,30,40,50]的高斯核作為基核(共8個)，運用FC-LMKELM進行診斷。首先對訓練樣本進行模糊C均值聚類，經試驗，當聚類數為4時可達到最佳性能，其隸屬度矩陣如表3所示。

基于表3所示的隸屬度信息，按照第3節中的步驟3～步驟6執行迭代更新過程，在不同的范數約束下，FC-LMKELM的學習曲線如圖7所示。

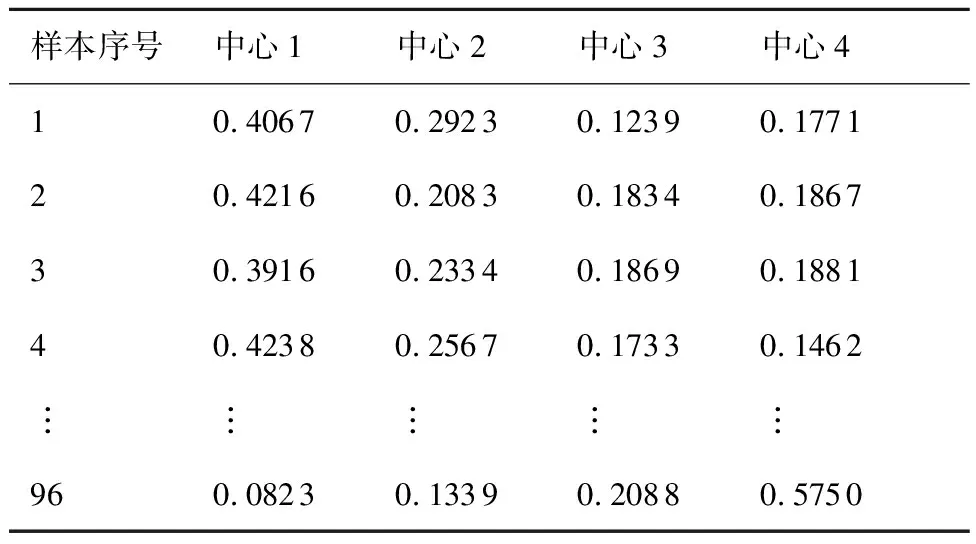
表3 診斷數據的隸屬度矩陣Table 3 Membership matrix of diagnosis dataset

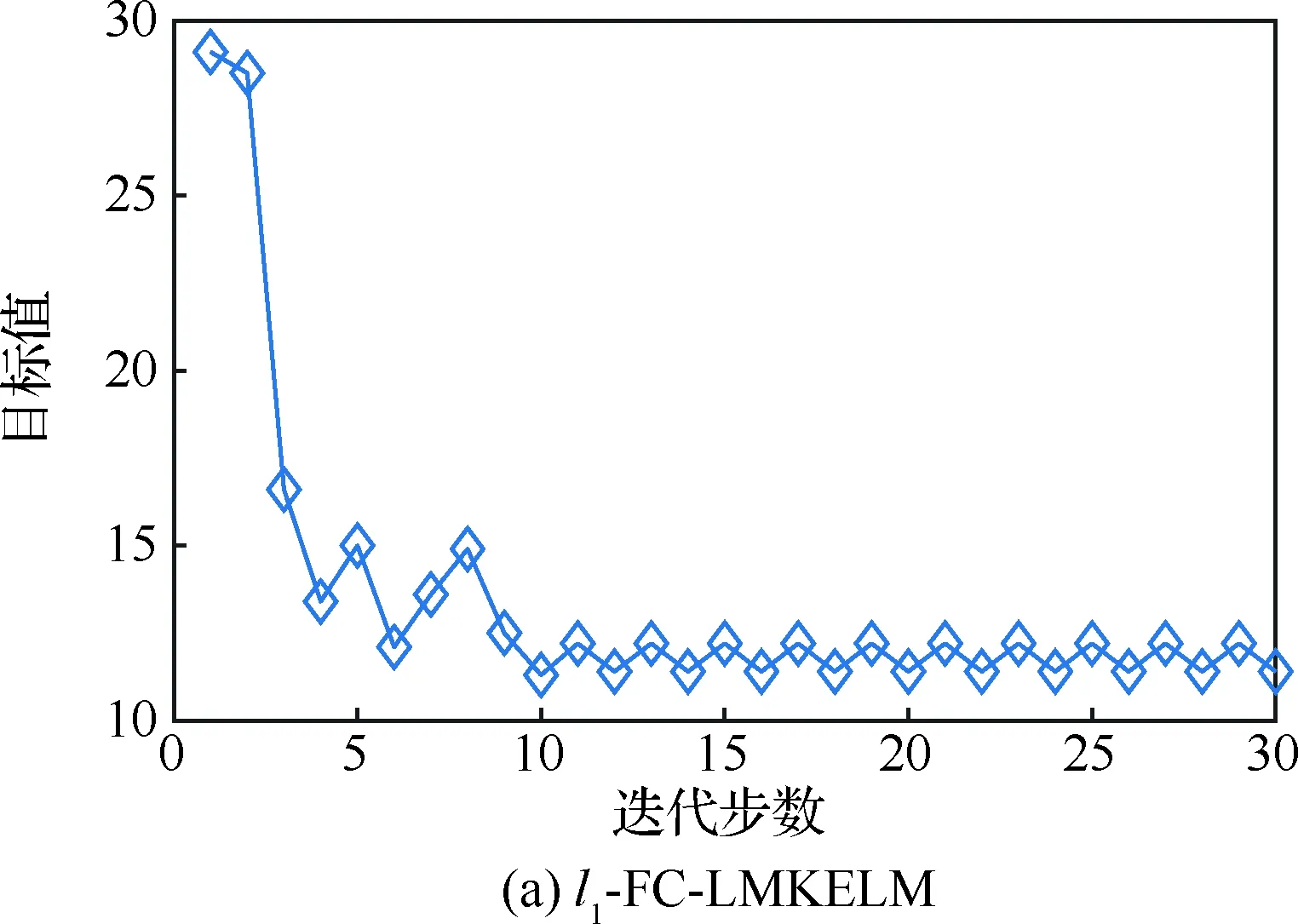
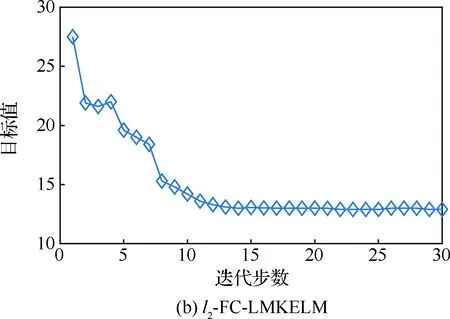
圖7 FC-LMKELM的學習曲線
Fig.7 Learning curves of FC-LMKELM

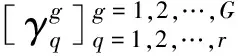
圖9以混淆矩陣的形式直觀地展示了FC-LMKELM與SimpleMKL、S-LMKL-softmax、S-LMKL-sigmoid、M2-LCMKELM的診斷效果。

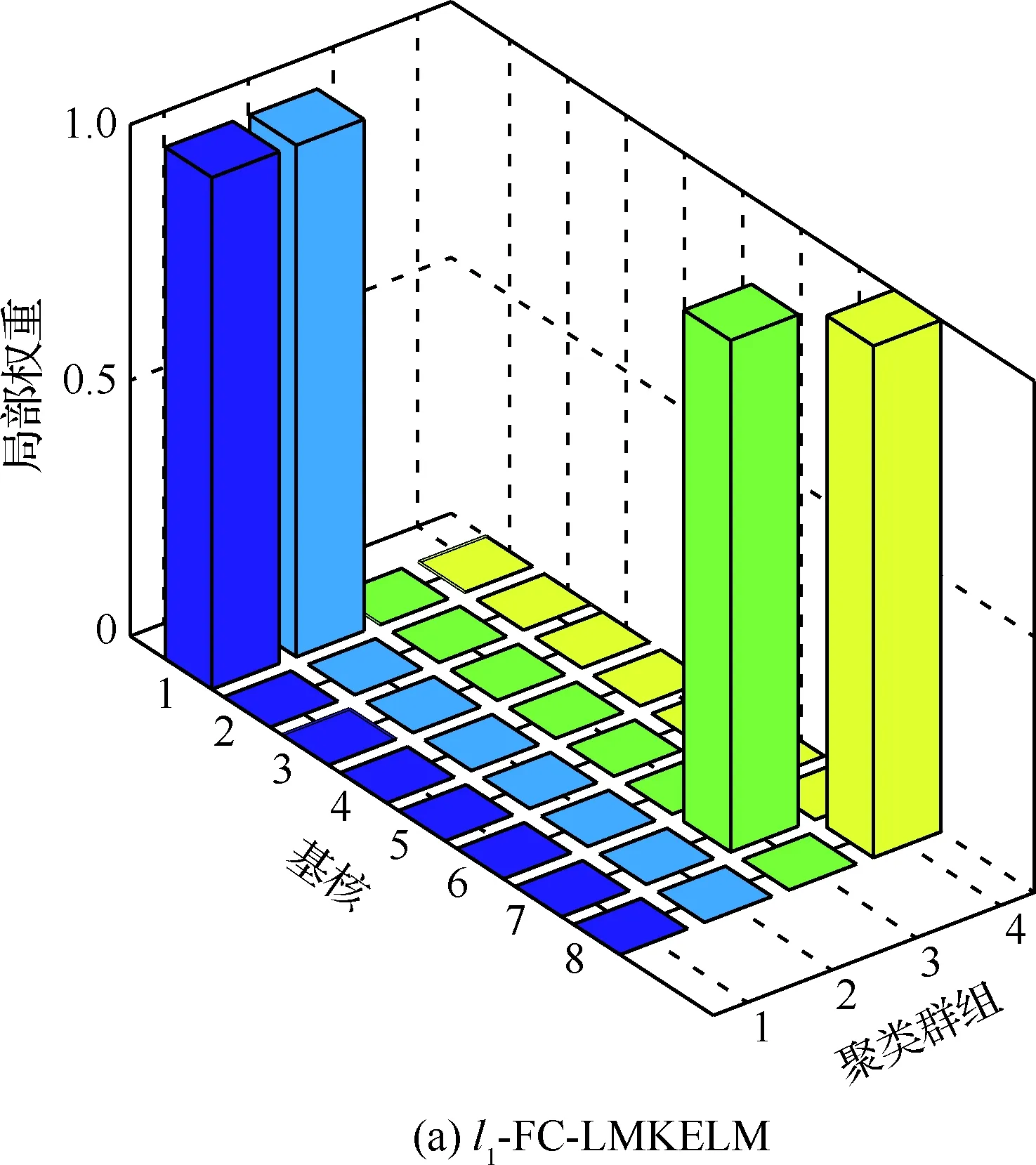
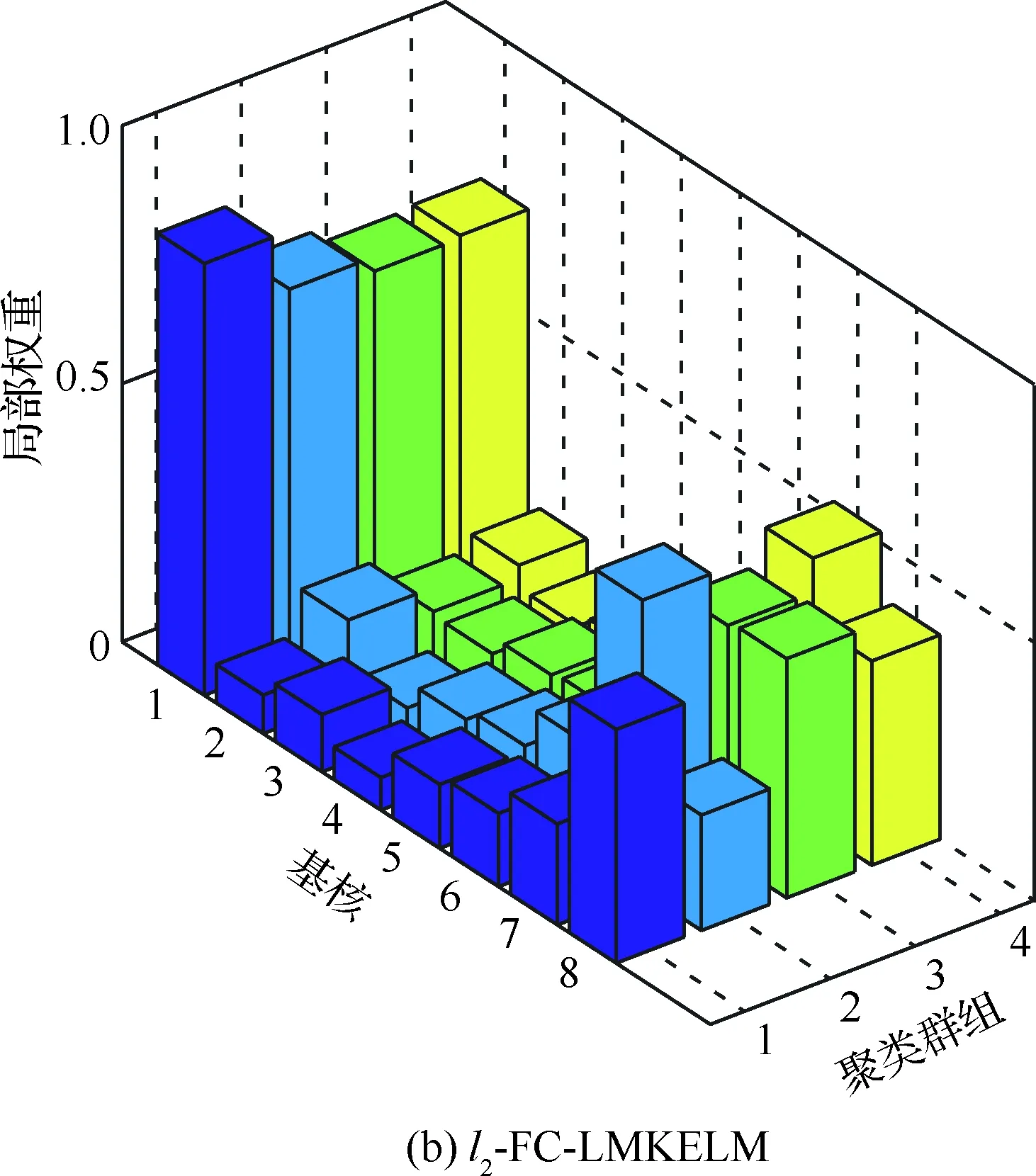
圖8 FC-LMKELM的局部權重分布

圖9 不同方法的混淆矩陣
Fig.9 Confusion matrices of different methods

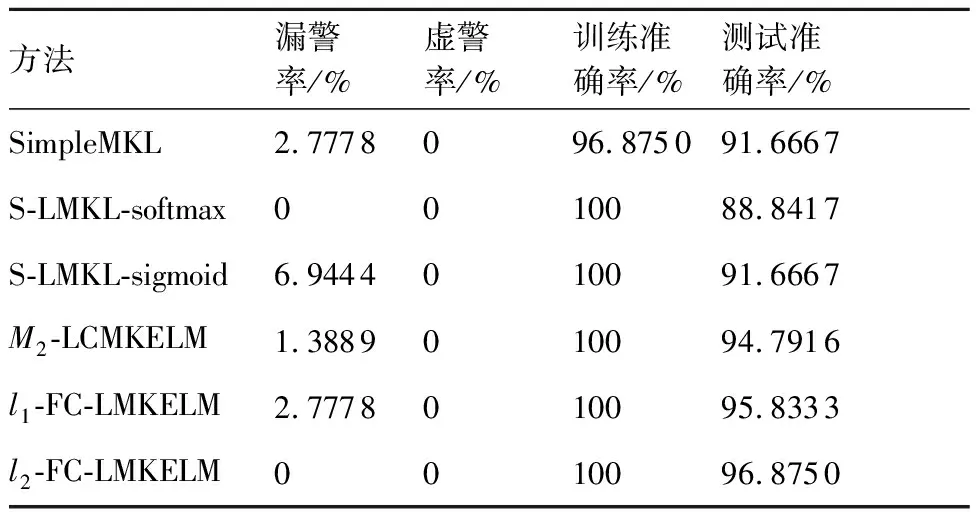
表4 各方法的指標值Table 4 Index values for different method

表4對各方法的精度指標進行了總結。由圖9和表4可知：

1) FC-LMKELM在避免漏警與抑制虛警方面表現優異，尤其是l2-FC-LMKELM，實現了0漏警，0虛警。

2) 兩種S-LMKL方法的測試診斷精度遠遠低于訓練診斷精度，顯然發生了嚴重的過擬合，其原因在于為每一個樣本點學習獨立的基核權重導致了算法泛化性能嚴重下降。與之相對的是M2-LCMKELM，通過“硬聚類”的方式將局部權重關聯至所屬聚類而非各個樣本上，既關注了局部特征又防止了過學習，泛化性能得以提升。

3) 由于融合了各個樣本對群組的隸屬度信息，相比于M2-LCMKELM，這種“軟聚類”的方式使FC-LMKELM的泛化性能得到了進一步的提升；l2-FC-LMKELM的診斷準確性比l1-FC-LMKELM高，原因在于后者的基核權重具有稀疏性(見圖8)，可能帶來有用信息的損失。相比其他4種非“軟聚類”方法，在測試精度方面，l1-FC-LMKELM分別提升了4.16%、6.99%、4.16%和1.04%；l2-FC-LMKELM則分別提升了5.20%、8.03%、5.20%和2.08%。

從另一個角度看，本節以文獻[28]中給出的適用于多分類問題的F1的推廣形式微觀F1(Micro-F1)、宏觀F1(Macro-F1)以及G-mean作為診斷方法的精確性評價指標，基于圖9的直觀結果將這3大指標統計于表5中，從中可知FC-LMKELM仍然表現最佳。

最后，為了探究所提方法的時效性，重復10次實驗，表6以“均值±標準差”的形式統計了各方法的時間開銷。

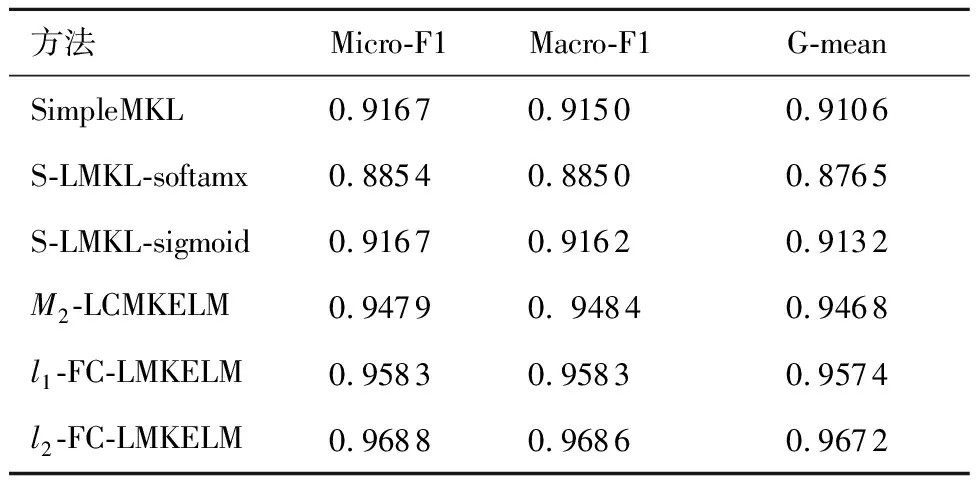
表5 各方法的F1分數和G-meanTable 5 F1 score and G-mean of different methods

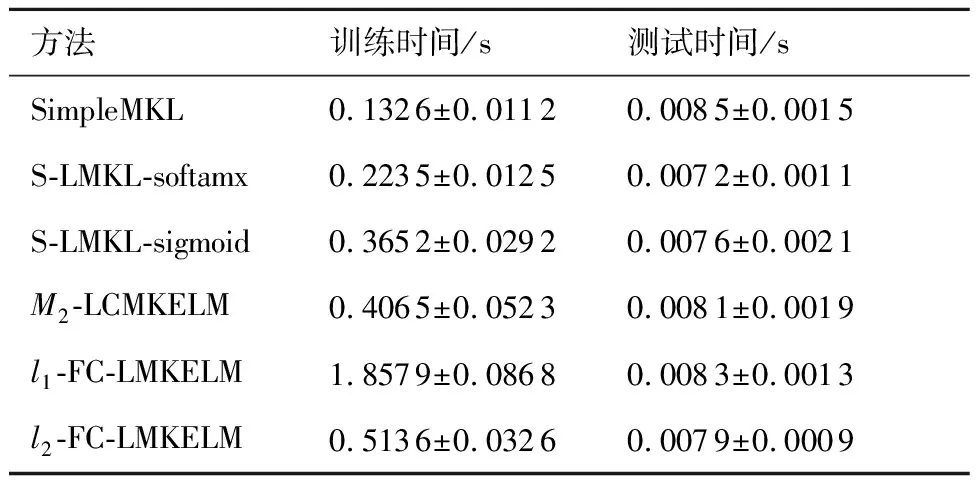
表6 不同方法的時間開銷Table 6 Time cost for different method

由表6可知：① 在訓練時間上，盡管FC-LMKELM要略長于其他方法，尤其在l1-范數約束下，每次迭代中加入的解線性規劃過程更多地延長了訓練時間，但需要注意的是，正如圖7所示，只需極少的迭代步數FC-LMKELM就能快速收斂，因此訓練時間開銷實際上是可控的；② 在測試時間上，FC-LMKELM與其他方法基本相同，均可實現實時輸出；③ 作為線下診斷方法，以少量時間開銷來換取更多的精確性上的提高是值得的；此外，航空電子部件的診斷多數情況下在小樣本條件下進行，時間花費不會過多，因此FC-LMKELM是有效的。

5 結 論

面向航空電子部件模塊級故障診斷問題，提出一種融合隸屬度信息的FC-LMKELM診斷方法。以某型機前端接收機的ATS測試數據為例，驗證了所提方法的有效性，可以得到以下結論：

1) 在診斷精度方面，相比于MKL方法和3種非“軟聚類”的LMKL方法，FC-LMKELM能夠有效避免漏警、抑制虛警并提升診斷精確度。對于某型機前端接收機，l1-FC-LMKELM和l2-FC-LMKELM比其他方法的平均值分別提高了4.09%和5.13%。

2) 在時間開銷方面，相比于MKL方法和3種非“軟聚類”的LMKL方法，FC-LMKELM訓練時間稍長，但較少的迭代次數確保了時間開銷的可控性；在測試時間上各方法基本在同一水平。

3) 聚類數量對所提方法的性能有很大的影響，并且沒有明確的規律可循，需要依據具體的數據進行驗證后確定。在訓練過程中融入聚類數量自適應變化的“軟聚類”方法是下一步的研究方向。