過虛擬交班點的能量最優(yōu)制導(dǎo)律
李晨迪,王江,李斌,*,何紹溟,張彤
1. 北京理工大學(xué) 宇航學(xué)院,北京 100081 2. 北京理工大學(xué) 無人機(jī)自主控制技術(shù)北京市重點實驗室,北京 100081 3. 北方華安工業(yè)集團(tuán),齊齊哈爾 161006
隨著現(xiàn)代軍事技術(shù)的發(fā)展,對精確制導(dǎo)武器的需求與日俱增,超視距導(dǎo)彈武器系統(tǒng)一般采用復(fù)合制導(dǎo)體制[1-3]。復(fù)合制導(dǎo)中,導(dǎo)彈由中制導(dǎo)轉(zhuǎn)為末制導(dǎo)時,交接班問題是實現(xiàn)精確制導(dǎo)的關(guān)鍵。為了使導(dǎo)引頭開機(jī)時順利截獲目標(biāo),實現(xiàn)中末制導(dǎo)交班,往往對此時導(dǎo)彈的位置等信息有一定要求[1],為了滿足對導(dǎo)彈中末制導(dǎo)交班的彈道約束,本文研究過虛擬交班點的制導(dǎo)律,為導(dǎo)彈提供可靠的中末制導(dǎo)交班條件。
近年來,基于軌跡跟蹤的制導(dǎo)律在無人飛行器領(lǐng)域被廣泛研究[4-5]。根據(jù)跟蹤方式,軌跡跟蹤法可分為兩類:連續(xù)軌跡跟蹤和路徑點(彈道點)跟蹤。與連續(xù)軌跡跟蹤相比,路徑點跟蹤只需要選取有限個彈道特征點,通過使導(dǎo)彈經(jīng)過選定的彈道點而得到期望彈道,計算量較小。連續(xù)軌跡跟蹤往往需要通過復(fù)雜計算實時得到待飛軌跡長度,或者基于虛擬目標(biāo)進(jìn)行軌跡跟蹤[6]。文獻(xiàn)[7]提出了一種兩點間線性二次最優(yōu)軌跡跟蹤制導(dǎo)律,用于跟蹤兩個彈道點之間的直線,其路徑改變點同樣基于需用過載最小得到,但該制導(dǎo)律不是全局最優(yōu)。文獻(xiàn)[8]提出了一種數(shù)值優(yōu)化方法,使得軌跡跟蹤制導(dǎo)律的能量消耗最小,計算復(fù)雜度較高。文獻(xiàn)[9]以反艦導(dǎo)彈為應(yīng)用背景,通過離線參數(shù)優(yōu)化得到每個彈道點的最優(yōu)邊界條件,例如角度和過載,從而在兩個彈道點之間采用最優(yōu)攻擊角度制導(dǎo)律,得到了全局能量最優(yōu)的軌跡跟蹤制導(dǎo)律。
有時,需要導(dǎo)彈以特定的終端落角對目標(biāo)進(jìn)行攻擊,以增強(qiáng)毀傷效果[10],近年來考慮終端角度約束的制導(dǎo)律受到廣泛關(guān)注。文獻(xiàn)[11-12]通過求解含剩余飛行時間的線性二次最優(yōu)控制方程得到含終端角度約束的最優(yōu)制導(dǎo)律的一般形式。文獻(xiàn)[13]應(yīng)用Schwarz不等式研究了帶落角約束的任意加權(quán)最優(yōu)制導(dǎo)律,得到了制導(dǎo)律的一般表達(dá)式。文獻(xiàn)[14]針對高速/低速目標(biāo)攔截問題,采用時變偏置角速率設(shè)計了一種三維聯(lián)合偏置比例導(dǎo)引律。文獻(xiàn)[15]研究了一種無剩余飛行時間的偏置比例導(dǎo)引律,在比例導(dǎo)引的基礎(chǔ)上加上角度約束偏置項,通過改變導(dǎo)彈過載實現(xiàn)終端角度約束。文獻(xiàn)[16]針對空地導(dǎo)彈具有終端角度約束的制導(dǎo)問題,提出了一種在有限時間內(nèi)穩(wěn)定的新型二階滑模變結(jié)構(gòu)制導(dǎo)律。
路徑點跟蹤制導(dǎo)問題在每兩個相鄰路徑點之間可以看作一般的制導(dǎo)問題,因此近幾十年研究得到的一些經(jīng)典導(dǎo)彈制導(dǎo)律同樣可以應(yīng)用于路徑點跟蹤問題。對于不考慮制導(dǎo)動力學(xué)滯后的制導(dǎo)問題,無終端落角約束時,導(dǎo)航比為3的比例導(dǎo)引為最優(yōu)制導(dǎo)律[17],當(dāng)考慮終端落角約束時,彈道成型制導(dǎo)律則成為最優(yōu)制導(dǎo)律[18-20]。但是在多個彈道點之間連續(xù)采用上述制導(dǎo)律的全局能量消耗是否為最優(yōu)尚未得到研究驗證[21]。基于此,本文將過虛擬交班點的精確制導(dǎo)問題視為路徑點跟蹤的特殊情況,即包括虛擬交班點與目標(biāo)點兩個彈道點,以氣動力控制的導(dǎo)彈為研究對象,分別研究了無落角約束與考慮終端落角約束情況下的全局最優(yōu)制導(dǎo)問題,推導(dǎo)出了解析解。最后,對非線性模型進(jìn)行仿真,結(jié)果表明,與經(jīng)典最優(yōu)制導(dǎo)律相比,無落角約束與考慮終端落角約束的情況下,該制導(dǎo)律可以將控制能量消耗分別減小49%和22%。
1 運動模型建立
1.1 非線性運動模型
為方便描述,將虛擬交班點與目標(biāo)落點視為兩個導(dǎo)彈需要經(jīng)過的路徑點,記作Pi(i∈{1,2}),導(dǎo)彈與目標(biāo)路徑點Pi之間的相對幾何關(guān)系如圖1所示。圖中:XIOYI為慣性坐標(biāo)系;V和a分別為導(dǎo)彈速度與法向過載;θ為彈道傾角;ri、qi和σi分別為導(dǎo)彈與第i個目標(biāo)路徑點之間的相對距離、彈目視線角和速度方向誤差角。
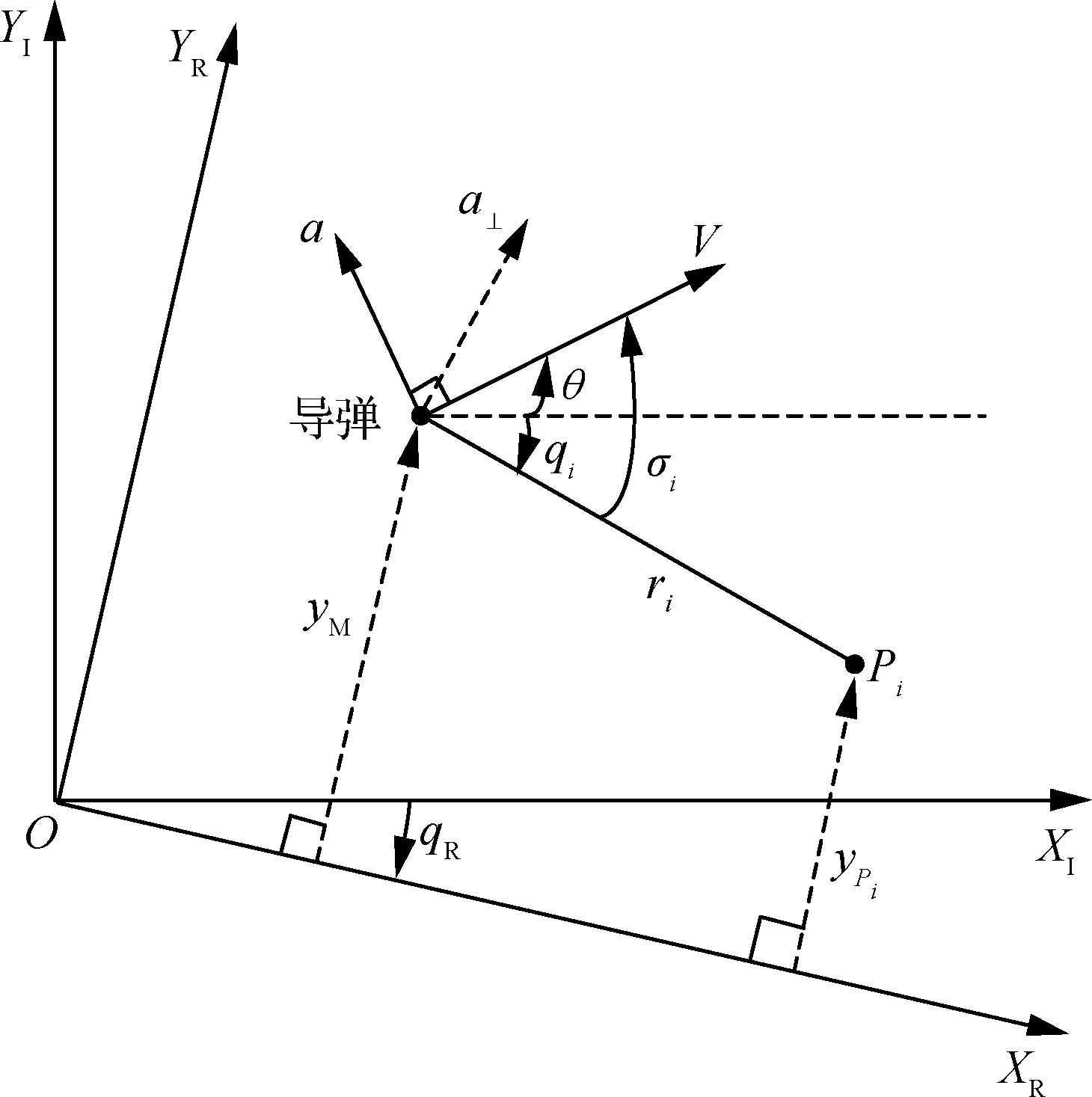
圖1 彈目相對運動關(guān)系
Fig.1 Missile-target engagement relationship
導(dǎo)彈與目標(biāo)路徑點之間的相對運動方程為
(1)
由幾何關(guān)系有
σi=θ-qi
(2)
1.2 模型線性化
本文將基于線性模型推導(dǎo)最優(yōu)制導(dǎo)律的解析解。引入?yún)⒖甲鴺?biāo)系,對建立的非線性運動學(xué)模型進(jìn)行線性化。如圖1所示,將坐標(biāo)系OXIYI繞原點旋轉(zhuǎn)qR角,得到參考坐標(biāo)系OXRYR。令yi=yPi-yM為導(dǎo)彈與Pi之間垂直于XR軸方向的相對位移,由幾何知識,yi=0?ri=0。
在參考坐標(biāo)系XROYR下,彈目相對運動方程可表示為
(3)
式中:vi、ai分別為導(dǎo)彈與Pi之間垂直于XR軸方向的相對速度與過載,由幾何關(guān)系可得
a⊥=acosσi
(4)
在工程實際當(dāng)中,飛行彈道由無控段、中制導(dǎo)段與末制導(dǎo)段3部分組成,對于中制導(dǎo)段與末制導(dǎo)段,可在每段飛行過程中分別視為彈目視線角變化較小,因此通過選取合適的qR可以使qi-qR為小量。同時,在實際情況中,導(dǎo)彈速度方向誤差角σi也為小量。基于以上合理假設(shè),式(3)可改寫為
(5)
記系統(tǒng)狀態(tài)向量為x=[x1,x2]T=[y1,v1,y2,v2]T,輸出向量為y=[y1,y2]T,線性化的系統(tǒng)狀態(tài)方程可以寫為
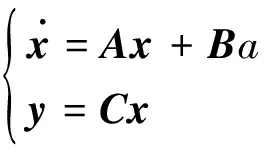
(6)
式中:
(7)
2 最優(yōu)控制問題描述
為得到控制量的全局最優(yōu)解,提出以下形式的性能指標(biāo):
(8)
式中:tf,i為導(dǎo)彈到達(dá)第i個路徑點的時刻。
本文研究的過虛擬交班點的固定目標(biāo)最優(yōu)控制問題可以表述如下。
問題1過定點的最優(yōu)制導(dǎo)律問題
對線性化的系統(tǒng)(6),解得使性能指標(biāo)(8)取極小值的制導(dǎo)指令a,并滿足約束:
yi(tf,i)=0i∈{1,2}
(9)
問題2帶終端落角約束的過定點最優(yōu)制導(dǎo)律問題
對于帶有終端落角約束的最優(yōu)控制問題,在上述無落角約束情況下,需額外滿足約束
θ(tf,2)=θd
(10)
式中:θd為期望落角。
3 過定點的最優(yōu)制導(dǎo)律設(shè)計
本節(jié)根據(jù)取控制能量最小的性能指標(biāo),選取零控脫靶量(ZEM)[19]作為唯一狀態(tài)變量,對系統(tǒng)進(jìn)行變換,從而實現(xiàn)系統(tǒng)降階,對上述兩個最優(yōu)控制問題進(jìn)行推導(dǎo),以得到最優(yōu)制導(dǎo)律的解析解,并對其進(jìn)行分析。
3.1 系統(tǒng)降階
為了方便對最優(yōu)解的解析形式進(jìn)行推導(dǎo),對狀態(tài)向量進(jìn)行坐標(biāo)變換,使系統(tǒng)降階。以第i個點為例,進(jìn)行變換
(11)
式中:變換矩陣Φi(tf,i,t)為
(12)
其中:tgo,i為導(dǎo)彈至第i個點的剩余飛行時間(time-to-go),將式(12)代入式(11)可得
(13)
得到Zi即零控脫靶量,它表示從當(dāng)前時刻起,導(dǎo)彈不再執(zhí)行任何控制指令的情況下到達(dá)第i個點的脫靶量。
對式(13)求導(dǎo)可得
(14)
經(jīng)過以上狀態(tài)變換,系統(tǒng)(6)由4階降為2階。
3.2 最優(yōu)制導(dǎo)律設(shè)計
對于變換后的系統(tǒng),最優(yōu)控制問題1轉(zhuǎn)化為在相同性能指標(biāo)下,對系統(tǒng)(14)求最優(yōu)解,即找到適當(dāng)?shù)腶使Zi盡快減小到0,同時控制能量最小。
根據(jù)ZEM的物理意義,新的系統(tǒng)狀態(tài)的終端約束為
Zi(tf,i)=0i∈{1,2}
(15)
根據(jù)線性系統(tǒng)理論,式(14)可改寫為
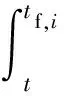
(16)
將式(15)代入式(16),可得
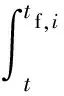
(17)
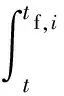
定理1H為希爾伯特空間,{α1,α2,…,αn}為H中的一個線性無關(guān)集,c1,c2,…,cn為一組已知常數(shù),在H中滿足約束條件(x|α1)=c1,(x|α2)=c2,…,(x|αn)=cn的所有解構(gòu)成一個集合V,此時V是一個余維數(shù)為n的線性流型,若xmin∈V,并且具有最小范數(shù),則有
bi滿足:
對于最優(yōu)控制問題1,式(17)中a(τ)與tf,i-τ分別對應(yīng)定理1中的x與αi,由定理1可得,含有拉格朗日乘子λi的最優(yōu)解形式為
(18)
式中:拉格朗日乘子λi即定理1中的bi。
以t≤tf,1為例,求解拉格朗日乘子的表達(dá)式。將式(18)代入式(17),可得
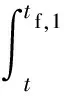
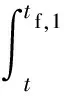
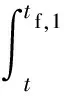
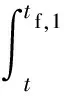
(19)
同理可以求得
(20)
定義λ=[λ1,λ2]T,Z=[Z1,Z2]T,由式(19)和式(20)可得
Z=Gλ
(21)
式中:
(22)
由式(21)可得
λ=G-1Z
(23)
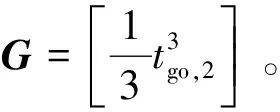
將式(23)代入式(18),可最終得到
(24)
3.3 討論與分析
為了更好地理解上述推導(dǎo)得到的制導(dǎo)律,進(jìn)行如下分析與討論。
討論1用tf,i=t+tgo,i計算到達(dá)時間,當(dāng)導(dǎo)彈位于路徑點附近時,可以視為得到精確的到達(dá)時間。
討論2考慮到實際應(yīng)用問題,對式(24)中的Z作如下處理:由于qi-qR為小量,所以有
(25)
求導(dǎo)得
(26)
由式(26)可得
(27)
在實際工程應(yīng)用中,由彈目視線角速率、速度和彈目距離等可測物理量,可計算得到制導(dǎo)指令。
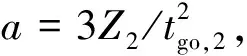
(28)
這與經(jīng)典的比例導(dǎo)引制導(dǎo)律(Proportional Navigation Guidance, PNG)形式一致。根據(jù)文獻(xiàn)[18],在只有一個目標(biāo)點時,導(dǎo)航比為3的比例導(dǎo)引為最優(yōu)制導(dǎo)律,與式(28)一致。進(jìn)一步可以得出結(jié)論,僅在相鄰兩點之間連續(xù)采用比例導(dǎo)引并不是能量最優(yōu)的,因為比例導(dǎo)引只保證當(dāng)前段彈道能量最優(yōu),沒有終端落角約束,因此總的控制能量消耗與本文提出的最優(yōu)制導(dǎo)律不同。
討論4將t≤tf,1時刻的過載指令表達(dá)式展開得
(29)
將式(27)代入式(29),可得
(30)
式中:
(31)
式(30)與含有偏置項的比例導(dǎo)引(BPN)形式一致,將其看作導(dǎo)航比隨時間變化的BPN,根據(jù)文獻(xiàn)[14]有
(32)
式中:q0為與初始條件有關(guān)的常數(shù)。
(33)
此時,制導(dǎo)指令為
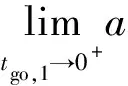
(34)
由于
(35)
可得
(36)
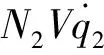
4 考慮終端落角約束的過定點最優(yōu)制導(dǎo)律設(shè)計
在一些情況下,需要導(dǎo)彈以一定的終端落角攻擊目標(biāo),以達(dá)到更好的毀傷效果。本節(jié)在第3節(jié)的基礎(chǔ)上加入終端落角約束,對有落角約束的過定點最優(yōu)制導(dǎo)律進(jìn)行設(shè)計。
4.1 最優(yōu)制導(dǎo)律設(shè)計
經(jīng)過系統(tǒng)降階后,第2節(jié)中的最優(yōu)控制問題2轉(zhuǎn)化為,對系統(tǒng)(14)求最優(yōu)解,使目標(biāo)函數(shù)達(dá)到極小值,并在滿足約束(15)的同時,還滿足以下終端落角約束:
θ(tf,2)=θd
(37)
由線性系統(tǒng)理論可得
(38)
過載指令由兩部分組成:
a=aZ+aθ
(39)
式中:aZ、aθ分別為與ZEM和彈道傾角相關(guān)的調(diào)節(jié)項。根據(jù)定理1,有
(40)
同樣地,以t≤tf,1為例求解拉格朗日乘子,將式(39)代入式(38)可得
(41)
由式(41)可得
(42)
式中:G1∈R2×2,G12∈R2×1,G21∈R1×2,由3.2節(jié)可知
(43)
下面求解G12、G21、G2:
(44)
可得
(45)
由式(42)~式(45)可以解得拉格朗日乘子為
(46)
可得過載指令為
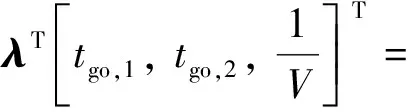
(47)
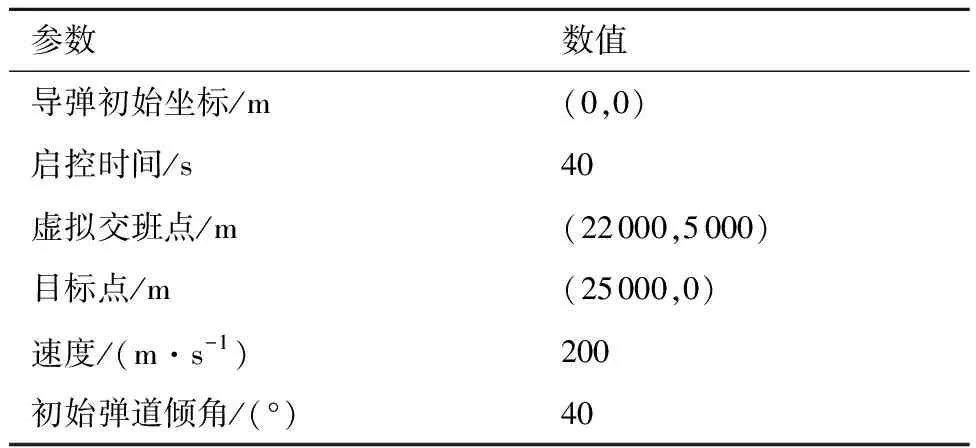
當(dāng)tf,1 (48) 過載指令為 (49) 注意到當(dāng)tf,1 (50) 對式(1)的第3項積分可得 (51) 將式(5)代入式(51),可得 (52) 又由式(13)可得 (53) 將式(52)、式(53)代入式(50),可得 (54) 與經(jīng)典的彈道成型制導(dǎo)律(Trajectory Shaping Guidance, TSG)形式一致。在只有一個目標(biāo)點,考慮終端落角約束的制導(dǎo)問題中,TSG是能量最優(yōu)的[18]。 本節(jié)以非線性系統(tǒng)為研究對象,對提出的制導(dǎo)律進(jìn)行仿真驗證,并與經(jīng)典最優(yōu)制導(dǎo)律進(jìn)行對比。飛行彈道包括無控段、中制導(dǎo)段與末制導(dǎo)段,導(dǎo)彈在40 s啟控后進(jìn)入中制導(dǎo)段,經(jīng)過虛擬交班點進(jìn)入末制導(dǎo)段,仿真參數(shù)如表1所示。 表1 仿真參數(shù)Table 1 Simulation Index 本節(jié)針對過虛擬交班點的無落角約束最優(yōu)制導(dǎo)律(24)進(jìn)行仿真驗證,并在中制導(dǎo)與末制導(dǎo)段分別采用最優(yōu)比例導(dǎo)引,即導(dǎo)航比為3的比例導(dǎo)引律,與本文提出的最優(yōu)制導(dǎo)律進(jìn)行對比。仿真結(jié)果如圖2所示。 圖2分別給出了2種制導(dǎo)律下的彈道、彈道傾角、過載指令和控制能量曲線。圖2(a)中五角星表示需要經(jīng)過的路徑點1(虛擬交班點位置)與路徑點2(目標(biāo)),可看出兩種制導(dǎo)律都可以準(zhǔn)確經(jīng)過目標(biāo)路徑點,但通過對比2條彈道曲線末制導(dǎo)段發(fā)現(xiàn),本文提出的最優(yōu)制導(dǎo)律比最優(yōu)比例導(dǎo)引制導(dǎo)律彈道更為平直;對比圖2(c),該最優(yōu)制導(dǎo)律在末制導(dǎo)階段的過載指令遠(yuǎn)小于最優(yōu)比例導(dǎo)引。且最優(yōu)比例導(dǎo)引的過載指令在虛擬交班點處出現(xiàn)跳變,本文提出的制導(dǎo)律下過載指令為連續(xù)的,最大需用過載不超過分段比例導(dǎo)引的36%。圖2(d)為2種制導(dǎo)律下的控制能量消耗,可以看出,本文提出的最優(yōu)制導(dǎo)律能量消耗大大減少,比最優(yōu)比例導(dǎo)引所需的能量消耗減少49%。 圖2 無落角約束情況下的仿真結(jié)果對比 本節(jié)對考慮終端落角約束的最優(yōu)制導(dǎo)律進(jìn)行仿真驗證。導(dǎo)彈期望落角選取為-90°。采用PNG與TSG切換的制導(dǎo)律進(jìn)行對比,即導(dǎo)彈在啟控后采用PNG,經(jīng)過虛擬交班點進(jìn)入末制導(dǎo)階段后,由PNG切換為TSG以實現(xiàn)期望落角。仿真結(jié)果對比如圖3所示。 對比發(fā)現(xiàn),圖3(a)與圖2(a)第一段彈道相同,而最優(yōu)制導(dǎo)律在加入終端落角約束后,末制導(dǎo)段彈道軌跡與彈道傾角變化較為明顯,因為本文提出的最優(yōu)制導(dǎo)律在開始時就將落角約束考慮進(jìn)去,從而得到全局最優(yōu)的制導(dǎo)律。圖3(c)給出了兩種制導(dǎo)律下的過載指令,可以看到在經(jīng)過虛擬交班點時,PNG+TSG下過載指令與無落角約束時一樣出現(xiàn)了不連續(xù)性,而本文提出的最優(yōu)制導(dǎo)律為連續(xù)的。圖3(d)為2種制導(dǎo)律所消耗的控制能量,對比發(fā)現(xiàn)本文提出的制導(dǎo)律所需控制能量比無落角約束時明顯增大,但仍比PNG+TSG下能量消耗減少22%。 圖3 考慮終端落角約束情況下的仿真結(jié)果對比 1) 本文在希爾伯特空間基于最優(yōu)化理論,提出了一種針對固定目標(biāo),過虛擬交班點的全局最優(yōu)制導(dǎo)律。在無落角約束下,能準(zhǔn)確經(jīng)過虛擬交班點,到達(dá)固定目標(biāo)點,且全局所需控制能量比最優(yōu)比例導(dǎo)引制導(dǎo)律減少了49%。 2) 在最優(yōu)制導(dǎo)律的基礎(chǔ)上考慮終端落角約束,推導(dǎo)出含終端落角約束的全局最優(yōu)制導(dǎo)律,該制導(dǎo)律可以實現(xiàn)期望落角,且全局所需控制能量比PNG+TSG下減少了22%。 3) 該制導(dǎo)律形式簡單,計算制導(dǎo)指令所需的信息較少,具有良好的工程應(yīng)用價值。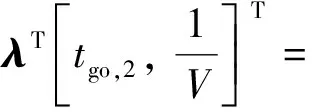
4.2 討論與分析
5 仿真驗證
5.1 無落角約束的最優(yōu)制導(dǎo)律仿真
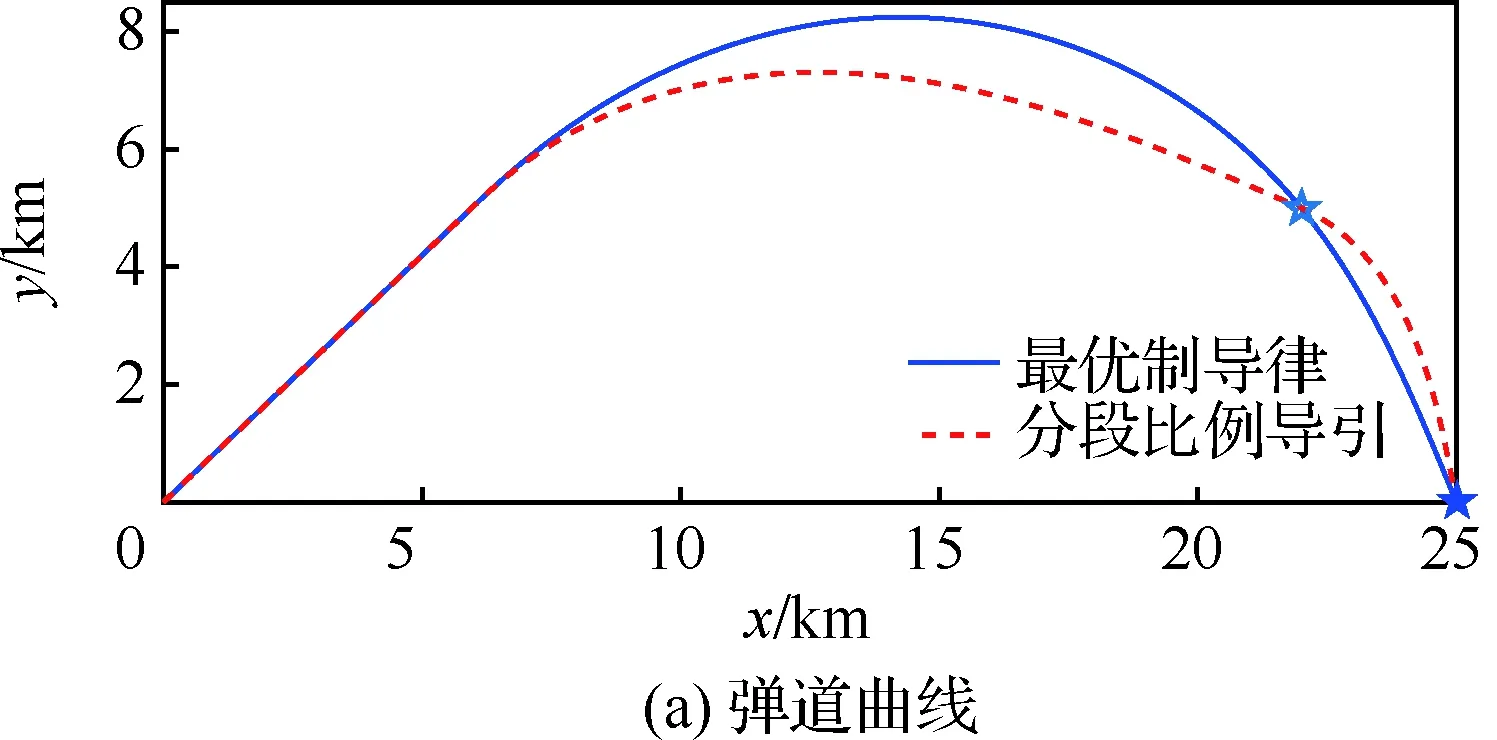
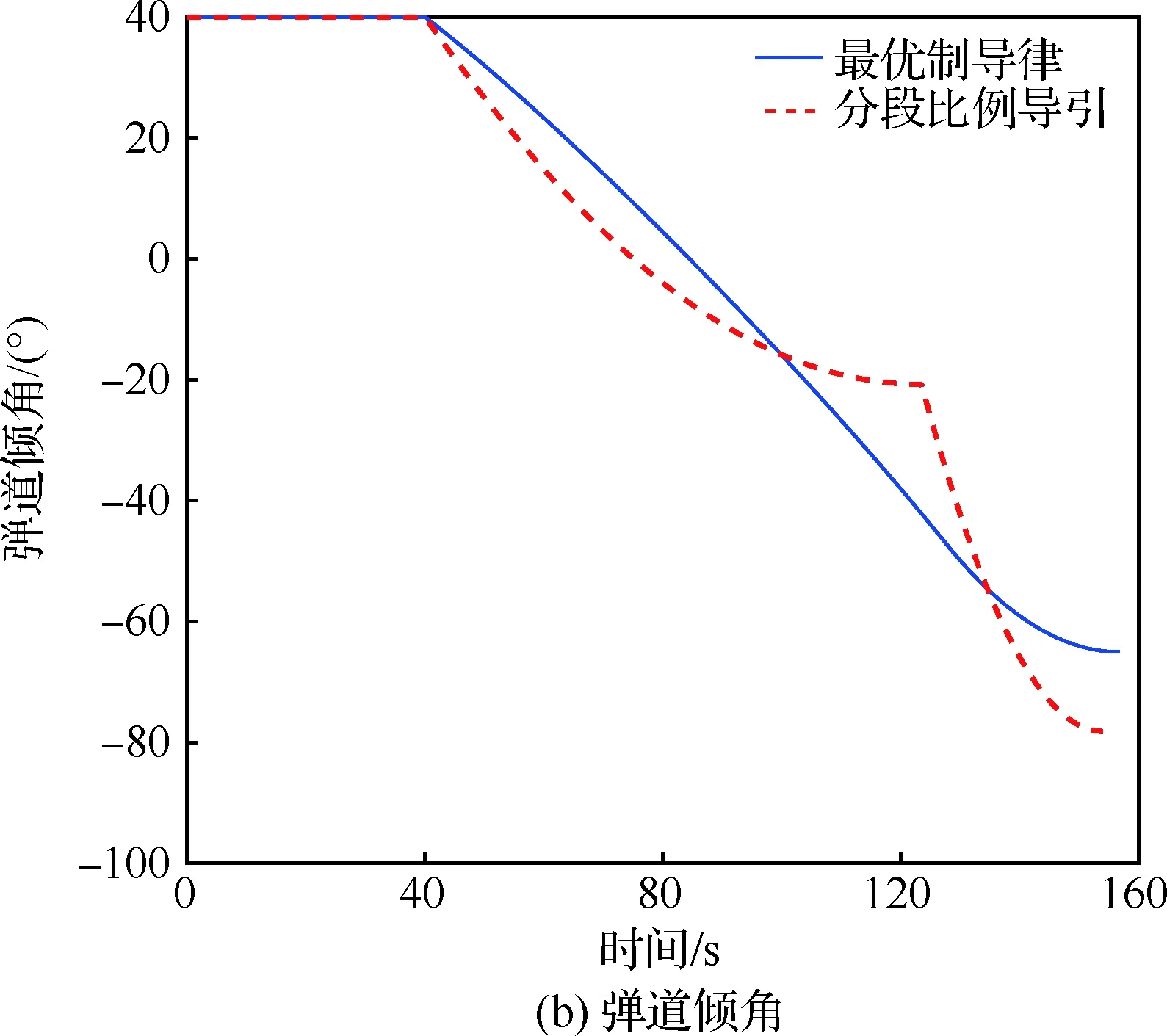
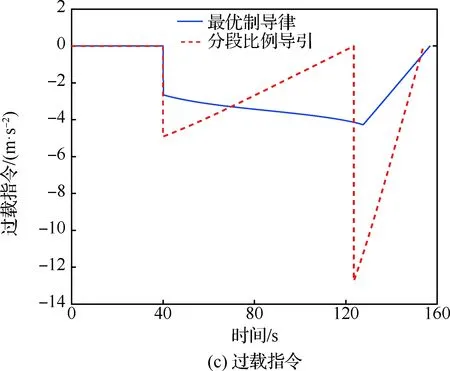
Fig.2 Comparison of simulation results without angle constraint5.2 考慮終端落角約束的最優(yōu)制導(dǎo)律仿真
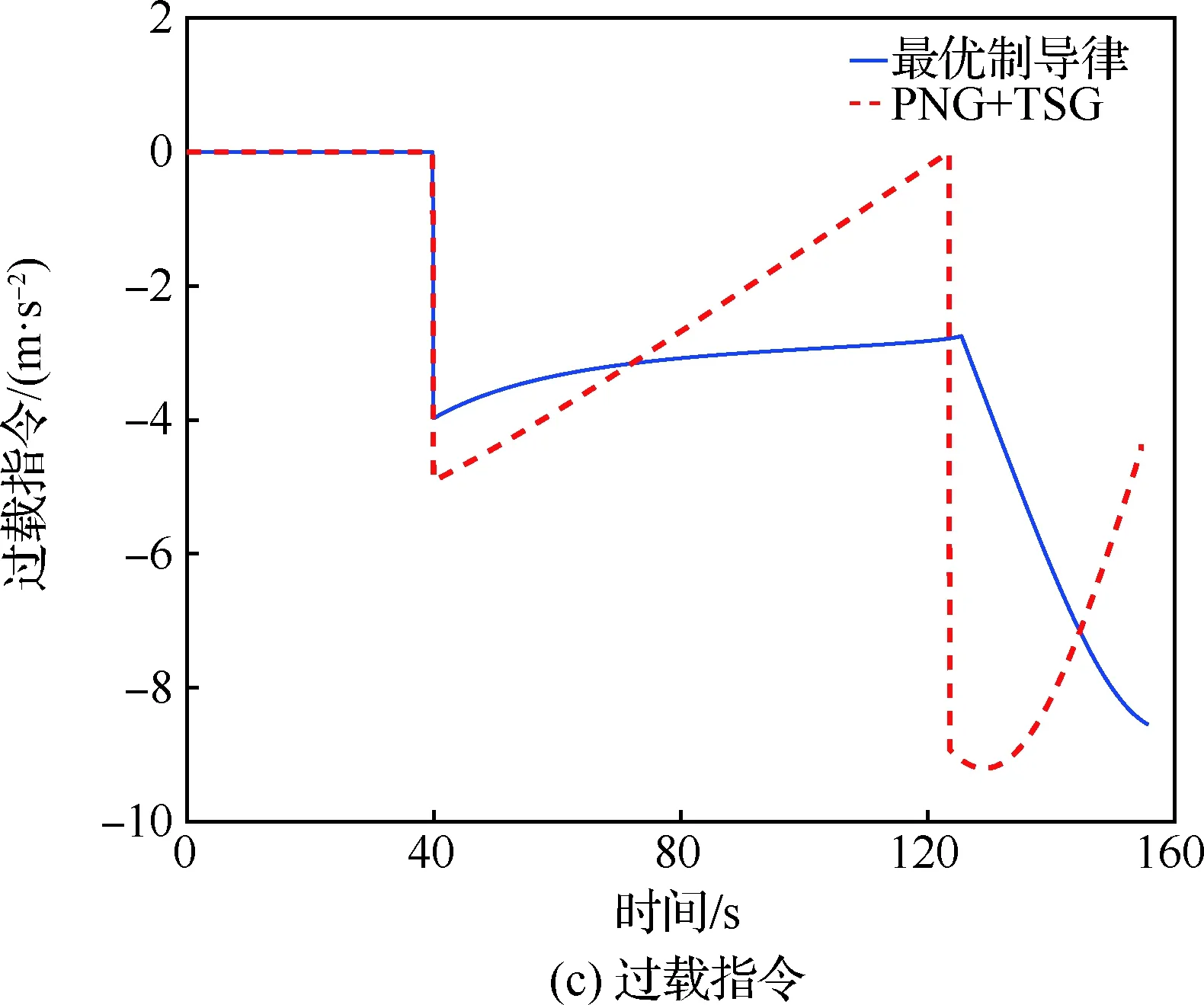
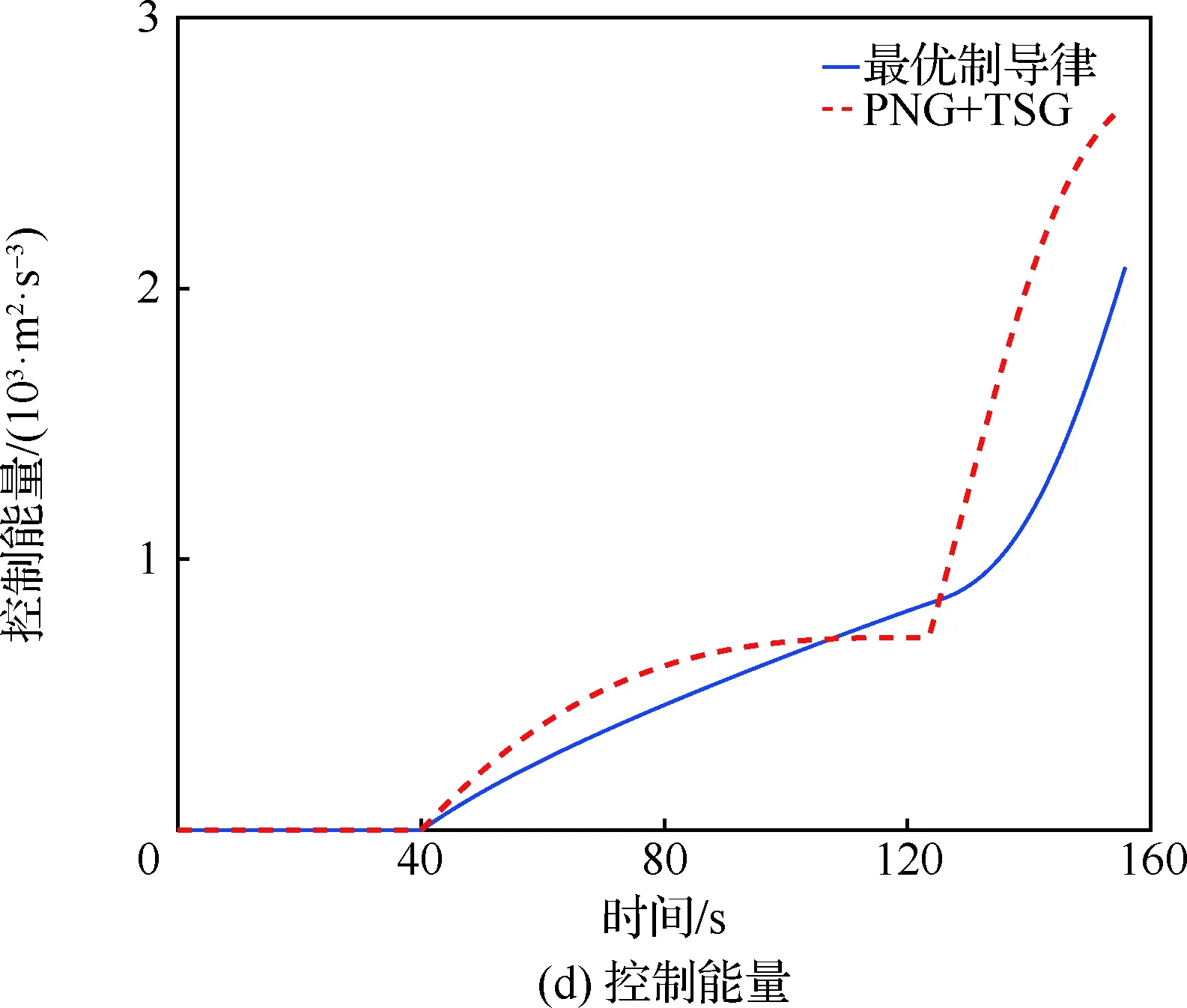
Fig.3 Comparison of simulation results with angle constraint6 結(jié) 論

