基于加速動態(tài)拉格朗日法的摩擦片阻尼分析
馬皓曄,李琳,2,范雨,2,*,吳亞光
1. 北京航空航天大學 能源與動力工程學院,北京 100083 2. 北京航空航天大學 航空發(fā)動機結構強度北京市重點實驗室,北京 100083
結構振動普遍存在于航空、航天、船舶等工程領域[1]中。過大的振動會導致結構的高周疲勞甚至失效,而增加阻尼是降低振動的有效方式。雖然對新型阻尼器的研究長盛不衰(如壓電分支阻尼技術[2-5]),但基于摩擦耗能原理的干摩擦阻尼器由于具有結構簡單、可靠性高、減振效果明顯且受溫度影響較小等優(yōu)點,仍是最常用且最受關注的阻尼技術之一[6-8]。在現(xiàn)役航空發(fā)動機中,就有多種形式的干摩擦阻尼器,如葉冠、葉片凸肩、緣板阻尼器、阻尼環(huán)等[9-12]。隨著未來飛行器對更高的推重比的追求,將進一步大量采用薄壁結構,這必然會導致更為突出的結構振動問題[9]。然而針對適用于一般薄壁結構的干摩擦阻尼器的研究尚不多見。
設計干摩擦阻尼器的關鍵技術之一是發(fā)展含接觸環(huán)節(jié)的非線性動力學模型及其求解方法。如果主要關注的是一類干摩擦系統(tǒng)的普適動力學行為,則常用集總參數(shù)模型,即將結構用少數(shù)幾個質量和彈簧的組合表征。研究人員已經(jīng)用這類模型探索了葉根阻尼器[13]、緣板阻尼器[14-16]、針對齒輪扭振的單個[17]和多個[18]阻尼環(huán)。集中參數(shù)模型的自由度很少,數(shù)值問題不突出,因此適合用于機理性研究或算法的合理有效性研究[19-20]。
如果主要關注的是具體的干摩擦阻尼器及其對所施加結構的減振效果(尤其是針對多個高階模態(tài)時),則應考慮使用高保真有限元模型。例如,張大義等[21]基于實體有限元模型建立了緣板阻尼結構的設計流程和優(yōu)化方法,并給出了結構設計合理性的評估參數(shù)。Petrov和Ewins[22]利用高保真有限元模型分析了帶冠葉片的強迫響應,并對屋頂形阻尼器(Cottage Roof Dampers, CRDs)與分離式阻尼器(Split Dampers, SDs)的減振性能進行了比較[23],并說明相比于CRDS,SDs對質量參數(shù)的變化不敏感。Charleux等[24]將榫接葉盤結構強迫響應的試驗與仿真結果進行對比,說明了利用高保真模型來預測帶接觸系統(tǒng)的振動特性是可行、可信的。高保真模型的自由度數(shù)一般較大,使得直接進行時域積分變得非常耗時,這就需要發(fā)展減縮模型和高效的頻域求解算法。目前常用動力凝縮和子結構方法減縮線性自由度的規(guī)模[25-26]。對于非線性自由度,可以在諧波平衡的框架內利用周期對稱性對葉盤等循環(huán)周期結構上的接觸點數(shù)目進行減縮[27];或對于一般結構,Krack等[28-29]還發(fā)展了非線性模態(tài)減縮技術,用以計算失諧榫接葉盤的強迫響應。目前最常用的頻域求解方法是諧波平衡法,即通過傅里葉變換將對非線性常微分方程的求解轉換為對非線性代數(shù)方程組的求解。即使針對集總參數(shù)模型,其計算效率遠高于時間積分法[30](CPU時間只是后者的約1%),但隨著自由度數(shù)的增加,諧波平衡法也面臨多個數(shù)值問題,其中的一個主要問題是用數(shù)值差分求雅克比矩陣的誤差導致牛頓-拉夫遜迭代難以收斂[31]。
本文提出一種適用于一般薄壁結構的波紋形干摩擦阻尼器,具有適用性強、正壓力調節(jié)方便、易于安裝等特點;并利用高保真有限元模型計算其頻響特性,展示其阻尼性能隨安裝螺栓壓緊力的變化規(guī)律。在計算方法上,采用了加速動態(tài)拉格朗日法對強迫響應進行預測,并給出了解析形式的雅克比矩陣,使算法的精度和速度得以大幅提升。通過集中參數(shù)模型的算例說明了理論推導及程序編寫的合理與正確性。利用一個四邊固支的平板結構來說明波紋形摩擦片的阻尼性能。
1 波紋形摩擦阻尼片
本文所考慮的波紋形干摩擦阻尼片如圖1所示。阻尼片的2個接觸面對稱分布在安裝面兩側,通過振動時接觸面與底部承載結構之間的相對運動產生的摩擦來達到減振的目的。安裝面利用螺栓與螺母進行固定。
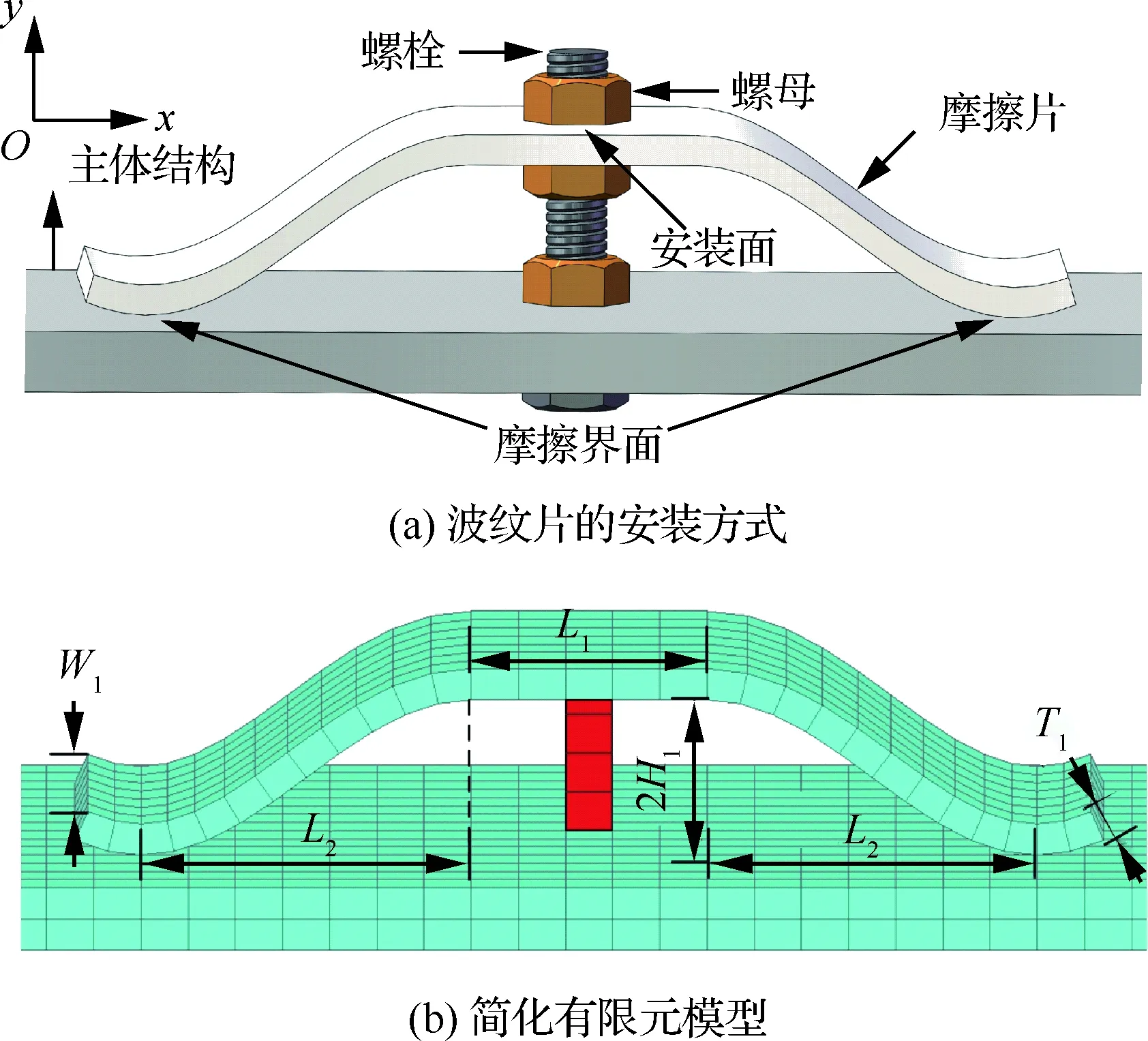
圖1 波紋形干摩擦阻尼器示意圖
Fig.1 Illustration of corrugated frictional patch
接觸面的正壓力是干摩擦阻尼器設計時的關鍵參數(shù),對干摩擦阻尼器的性能有著顯著的影響。當正壓力過小時,接觸面產生的切向力較小,導致由摩擦損耗的能量較小;當正壓力過大時,由于接觸面之間的相對滑移量減小,使得減振性能下降;當正壓力增大到使得接觸面達到“完全阻滯”狀態(tài)時,此時干摩擦阻尼器只有微小的調節(jié)固有頻率的作用,而不具備阻尼作用。對于圖1(a)所示的阻尼器,可以通過改變螺栓的擰緊程度來調節(jié)接觸面上的正壓力。
在對波紋形阻尼器的減振特性進行分析時,采用了如圖1(b)所示的有限元模型。其中T1、W1分別代表阻尼片的厚度與寬度。摩擦片的輪廓線(在xOy平面的投影)關于中心(安裝點)對稱,共由3段曲線構成:中間段為長為L1的直線,左右2段均為余弦曲線,滿足如下關系:
(1)
式中:L2為半波長;H1為波的峰值。直線段分別與兩邊的余弦曲線段相切。工作過程中會通過擰緊安裝面兩側的螺母來減小非摩擦界面處的相對運動,此時安裝面近似于固支狀態(tài),因此在有限元分析中,螺栓與螺母結構可用圖1(b)中位于安裝面區(qū)域內連接摩擦片與主體結構的實體單元來代替。接觸節(jié)點位于阻尼片下側的接觸面上,它們與主體結構上對應的節(jié)點重合。
接觸節(jié)點之間的相對運動相比于整體結構的振動幅值較小,因此可以采用點對點式的接觸單元來描述微滑移運動,如圖2所示。該模型又被稱為三維接觸運動模型,其中FN代表法向正壓力,由接觸對之間沿法向的相對位移決定,因此其能夠考慮由于自身形變所導致正壓力改變;FT1與FT2分別代表接觸平面上2個正交方向的摩擦力,在計算中認為它們是互不影響的[32]。該模型能夠完備地描述三維空間中接觸對之間的運動關系,在對高保真有限元模型研究時應用較為廣泛[22-23,26]。
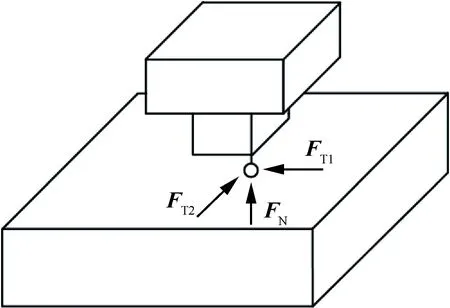
圖2 三維接觸運動模型示意圖
Fig.2 Illustration of 3D contact movement model
2 干摩擦結構響應的快速預測
為了展示波紋形干摩擦阻尼片的減振效果,用頻響函數(shù)的峰值作為評價指標。為此,采用了基于時頻轉換(Alternating Frequency-Time domain, AFT)的速度型動態(tài)拉格朗日法[26](Dynamic Lagrange Frequency-Time method, DLFT)。相比于以遲滯彈簧模型為基礎的強迫響應預測算法[27],DLFT的主要優(yōu)點為:① 不需要確定切法向彈簧剛度的值,同時計算結果對引入的懲罰系數(shù)的值不敏感[33];② 時域內不需要通過迭代來使得非線性力滿足周期條件[34]。在此基礎上,引入了解析形式的雅克比矩陣使得算法的計算效率與收斂穩(wěn)定性大幅提升。
2.1 高階諧波平衡法求解非線性動力學方程
對于帶有干摩擦阻尼的非線性系統(tǒng),其離散形式的動力學方程可以寫為
(2)
式中:M、C和K分別為質量、阻尼和剛度矩陣;qex(t)為外激振力向量,在本文中僅考慮其為時間的簡諧形式;qnl(t)代表作用于摩擦界面處的非線性干摩擦力,包括了切向與法向分量;u(t)為位移向量;上標(·)代表對時間的一次求導。直接在時域內求解式(2)這樣的2階非線性微分方程組將會耗費大量時間,尤其當自由度較多且求解的是穩(wěn)態(tài)響應時,計算時間成本將迅速增加。故本文在頻域內采用高階諧波平衡法求解式(2)的穩(wěn)態(tài)強迫響應。
高階諧波平衡法的出發(fā)點是將位移、外激勵和非線性力表示成傅里葉級數(shù),并截取前Nh項。因此,位移項u(t)可寫為

(3)
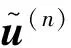

(4)
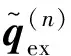

(5)
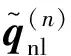
(6)
由于ejnωt≠0,因此只能前面括號里的向量為零,從而獲得一組非線性代數(shù)方程組:
(7)
式中:H(n)為第n階諧波的動剛度矩陣,即
H(n)=-(nω)2M+jnωC+K
(8)
在解該非線性代數(shù)方程組時,一般常用“牛頓-拉夫遜”迭代法以及其改進方法[15]。然而隨著方程自由度的提高,計算效率與穩(wěn)定性都會明顯下降。注意到相對于整個結構系統(tǒng),接觸面只占很小一部分,因此本文進行自由度凝縮,以減少迭代時方程的自由度。首先,將式(7)中的向量和矩陣分成線性自由度(下標l)與非線性自由度(下標nl):
(9)
再通過凝聚,僅保留非線性自由度:
(10)
(11)
這樣,總自由度從(Nl+Nnl)×(Nh+1)變?yōu)镹nl×(Nh+1),其中Nl和Nnl分別為線性自由度數(shù)與非線性自由度數(shù)。
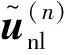
(12)
式中:S(n)=[D(n)]-1。對于任意一組接觸點,引入相對位移:
(13)
聯(lián)立方程式(12)與式(13),則動力學方程組可最終表示為相對位移的形式:
(14)
其中:
(15)
由此,方程組的自由度數(shù)進一步降低到原來的一半,即Nnl×(Nh+1)/2。在對式(14)進行求解時,一般將其寫為收斂殘差的形式,即
(16)
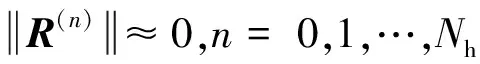
2.2 速度型動態(tài)拉格朗日法求解非線性力
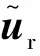
(17)
并用如下關系計算非線性力:
(18)
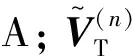
式(17)可以看做是在式(14)的基礎上,分別在切向(下標T)引入了一個關于相對速度的懲罰項以及在法向(下標N)引入了一個關于相對位移的懲罰項,其中ε為懲罰系數(shù)。
(19)
利用傅里葉逆變換,將式(19)的每一項都變換到時域,此時每個自由度的運動都被離散至Ns個時間點上,其中任意第l個時間點下的拉格朗日乘子λ(l)可表示為
λ(l)=λu(l)-λx(l)
(20)
注意此時實際上已知的是λu,λ和λx暫時是未知的,采用下面的預測-修正方法求得。
對于任意接觸點k,首先假設其在時間步l處為阻滯狀態(tài),即2個接觸點之間沒有相對運動,因此kλx(l)=0,得到非線性力的預測值:
kλpre(l)=kλu(l)
(21)
再利用庫倫摩擦定律來判斷該點的真實接觸狀態(tài),并用kλx(l)對非線性力進行修正,共有如下3種情況:
1) 分離:|kλpre,N(l)|+|N0|≤0,其中N0代表施加在接觸點上的初始正壓力。此時接觸對之間不存在接觸力的作用,即kλ(l)=0,此時:
kλx(l)=kλu(l)
(22)
2) 阻滯:|kλpre,N(l)|+|N0|>0,同時切向力|kλpre,T(l)|<μf|kλpre,N(l)+N0|。其中μf代表接觸面的摩擦系數(shù)。滿足此條件時,說明當前的接觸狀態(tài)與預測結果相吻合,無需對非線性力進行修正,即
kλx(l)=0
(23)
3) 滑移:|kλpre,N(l)|+|N0|>0,同時切向力|kλpre,T(l)|≥μf|kλpre,N(l)+N0|。此時法向接觸點之間相對位移的值為0;切向存在相對運動,且根據(jù)庫倫摩擦定律,切向摩擦力的大小可表示為μf|kλpre,N(l)+N0|,方向與相對速度的方向一致,因此可以得到滑移狀態(tài)下的修正項:
(24)
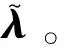
需要注意的是,基于牛頓-拉夫遜法的迭代方法為局部收斂法,即當給的初值與方程的解較接近時,該方法具有較強的數(shù)值穩(wěn)定性,反之方程容易不收斂。因此在求解頻域內的強迫響應時,可以采用自適應步長的自然延拓法從小到大進行掃頻計算,并以上一個頻率點的迭代收斂解作為計算下一個頻率點強迫響應的迭代初值。對于第一個頻率點,一般將遠離共振峰處系統(tǒng)不受非線性力作用下相對位移的頻域值作為迭代初值。
2.3 用解析雅克比矩陣加速計算
在利用牛頓-拉夫遜法以及其改進方法進行迭代時,其中必要的一步則是用非線性代數(shù)方程組式(15)的雅克比矩陣來判斷下一次迭代的值,在MATLAB中用fsolve函數(shù)解非線性方程組時,默認情況下該矩陣一般通過有限差分法給出。然而當方程中的非線性自由度數(shù)較大時,利用數(shù)值差分計算雅克比矩陣的時間成本較大,且精度也較低。如果能給出解析形式的雅克比矩陣,就能夠有效地解決這一問題[27]。因此,給出適用于速度型動態(tài)拉格朗日法的解析雅克比矩陣。
對于收斂殘差形式的運動方程(16),其雅克比矩陣可寫為
(25)
式中:Dr直接通過式(15)計算得到,因此計算J的關鍵就在于求解拉格朗日乘子對于相對位移矢量的偏導。利用求導的鏈式法則,式(25)的第2項寫為
(26)
其中:
(27)
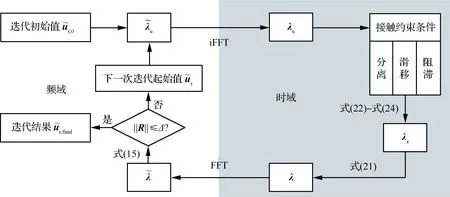
圖3 基于時頻轉換的動態(tài)拉格朗日法流程
Fig.3 Flowchart of DLFT based on time-frequency conversion
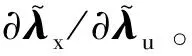
(28)
(29)
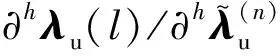
(30)
?kλx,N(l)/?hλu,T(l)的值為0。另外2種情況則為切向的修正項關于切向的預測項的偏導?kλx,T(l)/?hλu,T(l):
(31)
以及切向的修正項關于法向的預測項的偏導?kλx,T(l)/?hλu,N(l):
(32)

(33)
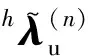
(34)
通過式(25)~式(34)即可獲得雅克比矩陣的解析表達式,從而提高利用DLFT法預測系統(tǒng)強迫響應的計算效率與數(shù)值穩(wěn)定性。
2.4 計算流程簡述
圖4給出了針對具有摩擦片的有限元模型強迫響應預測算法的計算流程,概述如下:① 利用標準有限元軟件(本文使用ANSYS)對帶有波紋形干摩擦阻尼片的結構的線性部分進行建模;② 提取系統(tǒng)的剛度矩陣K、質量矩陣M與阻尼矩陣C;③ 對得到的K、M、C矩陣進行固定界面模態(tài)減縮,僅保留少量的主節(jié)點自由度。值得注意的是,該減縮僅在生成待求解代數(shù)方程組的過程中進行一次;④ 將方程的自由度凝聚到非線
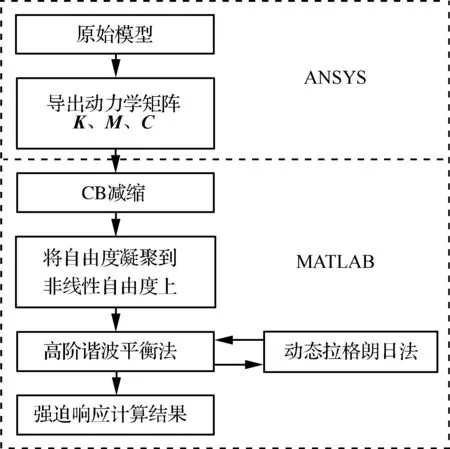
圖4 基于減縮模型的DLFT計算流程
Fig.4 Flowchart of DLFT based on reduced order model
性自由度上,進一步減少計算規(guī)模;⑤ 利用圖3所示DFLT法求解非線性力的大小,在該步驟中采用時頻轉換技術,即先將頻域獲得的位移轉化到時域,并在時域內對非線性力進行修正,再將修正的非線性力轉回頻域;⑥ 將非線性力代回運動方程式(10),得到觀察點的強迫響應計算結果。
2.5 程序正確性測試
對于2.4節(jié)計算流程,可以通過如圖5所示的具有2個摩擦面的集中參數(shù)模型,將計算結果與基于切/法向剛度的時頻轉換技術(Elastic Frequency-Time technique, EFT)的結果進行比較,從而說明程序的正確性。
圖5中的模型分為上下2個結構,不同結構的質量塊之間存在接觸。在驗證模型中,每一個接觸點包含1個切向與1個法向。在上結構中,每一個質量塊受到大小為F的激振力激勵。模型中各參數(shù)的取值如表1所示。
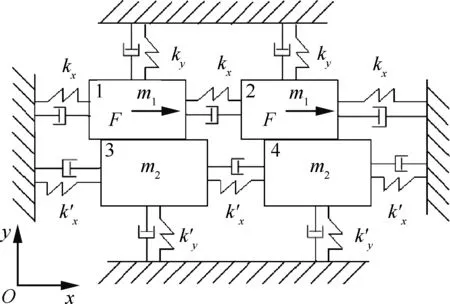
圖5 帶有接觸面的集中參數(shù)模型
Fig.5 Lumped parameter model with contact interfaces

表1 帶有接觸的集中參數(shù)模型參數(shù)
利用切向/法剛度法驗證速度型動態(tài)拉格朗日算法的正確性時,用如圖6所示的考慮接觸剛度的遲滯庫倫摩擦模型來描述接觸面的力學特征。該模型認為在阻滯狀態(tài)下,由于力的作用,接觸點之間仍存在一定的彈性變形,并通過引入切/法向彈簧來描述這一特征。在驗證模型中,切向彈簧與法向彈簧的剛度分別為kt,kn=1×107N/m。
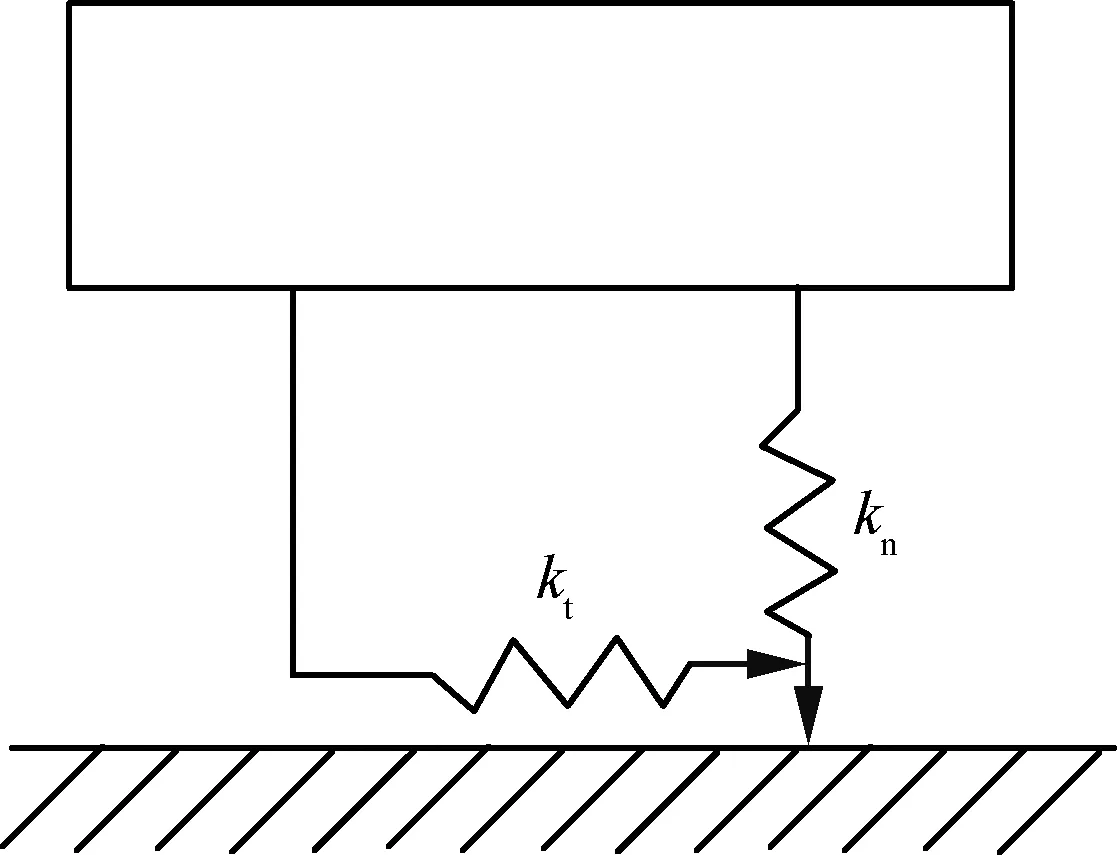
圖6 二維遲滯彈簧接觸模型示意圖
Fig.6 Illustration of 2D contact model with hysteresis springs
分別利用速度型動態(tài)拉格朗日法與切/法向剛度法計算該模型在不同正壓力下的強迫響應,其中觀測點為質量塊1沿著x方向的位移,同時上述2種方法都是基于解析雅克比矩陣的。兩者的結果對比如圖7所示。
圖7中標注的離散點為利用基于切/法向遲滯彈簧模型的NewMark法直接在時域內求得的特定頻率下的響應幅值。從圖7可以看出,利用切向/法向剛度法與速度型動態(tài)拉格朗日法的計算結果十分相近,其中存在的微小的差異是由于DLFT在時域上是利用不考慮遲滯彈簧的庫倫模型去滿足接觸約束的。該計算結果與文獻[33]中描述的現(xiàn)象相吻合。在計算時間上,以圖7為例,利用速度型動態(tài)拉格朗日法得到一條穩(wěn)態(tài)響應曲線平均所用的CPU時間為145.3 s,而利用切/法向剛度法平均所用的CPU時間為638.7 s,可見在計算結果近似的情況下,前者的計算效率要明顯高于后者。
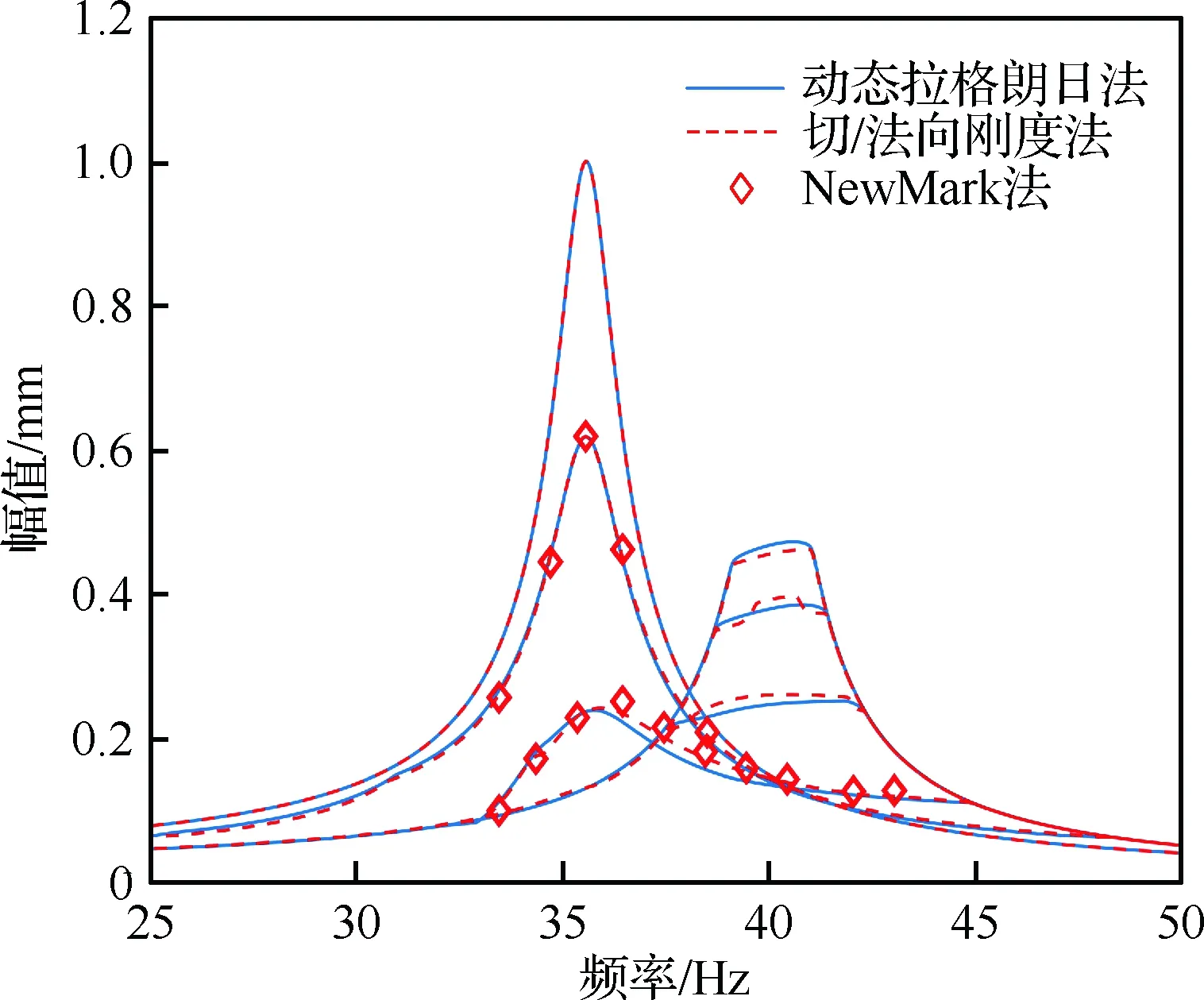
圖7 不同算法下強迫響應曲線的比較
Fig.7 Comparison of forced response curves using different algorithms
3 波紋摩擦片的減振效果分析
本節(jié)將用上述數(shù)值工具研究波紋形摩擦阻尼片對于薄壁結構的減振效果。注意到,干摩擦阻尼器的減振效果與系統(tǒng)在全阻滯與全滑移狀態(tài)下的共振頻率差相關。一般來說較大的頻率差對應著較好的減振性能[37]。因此阻尼片應該布置在能夠明顯調整主體結構在目標頻帶內的固有頻率的位置上。
平板結構為一種具有代表性的薄壁結構,本節(jié)通過在一塊405 mm×405 mm,厚度為2 mm的板上布置波紋形干摩擦阻尼片,利用仿真模擬的手段研究阻尼片減振性能。板由鋼構成,其材料參數(shù)為:彈性模量E=210 GPa,泊松比μ=0.3,密度ρ=7 800 kg/m3。邊界條件為板的四邊全部固支。
將第5階模態(tài)作為目標模態(tài),研究阻尼片對于由此模態(tài)所主導的振動的減振效果。其模態(tài)頻率為400.47 Hz,模態(tài)振型如圖8所示。將4片阻尼片布置到如圖9所示的位置,每片阻尼片都對應平板四條邊的中點,且其中一個接觸面位于固定端3 mm處。阻尼片的材料參數(shù)為:彈性模量E=70 GPa,泊松比μ=0.3,密度ρ=2 700 kg/m3。

圖8 四邊固支板的第5階模態(tài)振型
Fig.8 Modal shape of the 5th mode of four side fixed plate
阻尼片的幾何尺寸如表2所示。為激起該階模態(tài),在圖9中的施力點位置施加垂直于板方向的激振力,大小為F=15 N,同時相鄰2點之間的激振力存在π/2的相位差。
圖9 帶有4個阻尼片的板結構
Fig.9 Plate with four frictional patches attached
在分析時,首先建立圖9中含有阻尼片的板結構的有限元模型(利用ANSYS);再用固定界面模態(tài)減縮來降低模型的自由度,保留其中施力點與觀測點的線性自由度,以及接觸面上的所有非線性自由度。為保證計算精度,截取前50階模態(tài),由此得到的降階模型前10階的模態(tài)頻率與原模型相比,誤差小于0.5%,且模態(tài)振型相似性約等于1,故可以用此降階模型的計算結果來替代原模型。
利用DLFT方法對上述模型進行計算,模型本身的阻尼比取ξ=0.002,文獻[38]中表明摩擦系數(shù)的大小對干摩擦阻尼器的最優(yōu)減振效果并不敏感,這里該參數(shù)的取值為μf=0.6。為保證計算精度,本文中保留的諧波數(shù)為Nh=5,計算得到如圖10所示的不同正壓力下觀測點的穩(wěn)態(tài)強迫響應曲線。隨著正壓力的增大,共振頻率向右偏移,完全自由狀態(tài)下的共振頻率為400.6 Hz,與純平板結構下的固有頻率變化不大,說明當阻尼片布置在該位置時,其附加質量對整體結構的動力學特性幾乎沒有影響。當接觸面處于完全阻滯狀態(tài)時,共振頻率為408.4 Hz,頻率偏移量為7.8 Hz。共振幅值隨著正壓力的增加先減小,后增大。當初始正壓力為80 N時,阻尼片的減振性能最佳,共振幅值相對于完全分離狀態(tài)下降了75.4%。同時,阻尼片的質量(考慮了安裝所用的螺栓和螺母)占主體結構的0.6%。由此可見,該波紋形干摩擦阻尼器對于平板結構具有較為理想的減振性能。
還可以對接觸區(qū)域的局部動力學特性進行分析。以圖9中箭頭所指的接觸點為例,在初始正壓力為80 N下達到共振峰時,該接觸點在時域內的運動狀態(tài)如圖11所示。其中實線代表接觸點處所受的切向摩擦力,虛線代表接觸對之間的切向相對位移。當接觸狀態(tài)為阻滯時(陰影部分),接觸對之間的相對位移保持不變;當接觸狀態(tài)為滑移時,由于切法向運動耦合的影響,導致切向的摩擦力并不是定值。
關于計算效率,以最優(yōu)正壓力下計算強迫響應為例,所用的時間與減縮過程中系統(tǒng)的自由度的變化如表3所示。可見構造減縮模型所耗費的時間只占總分析時間的很小部分,卻能有效地降低模型的自由度(降低了99.7%),因此推薦在用DLFT分析較大規(guī)模的有限元模型時使用減縮技術。如果不采用解析雅克比矩陣而是用默認的數(shù)值差分近似,平均一個頻率點所需的CPU時間為333.7 s;采用減縮方法后,計算706個頻率點總共花了5 360.1 s,平均每1個頻率點的CPU計算時間為7.6 s。可見如式(25)~式(34)所示的解析雅克比矩陣對速度型的動態(tài)拉格朗日法的計算效率至關重要,在計算自由度相對較多的結構時幾乎是不可或缺的。
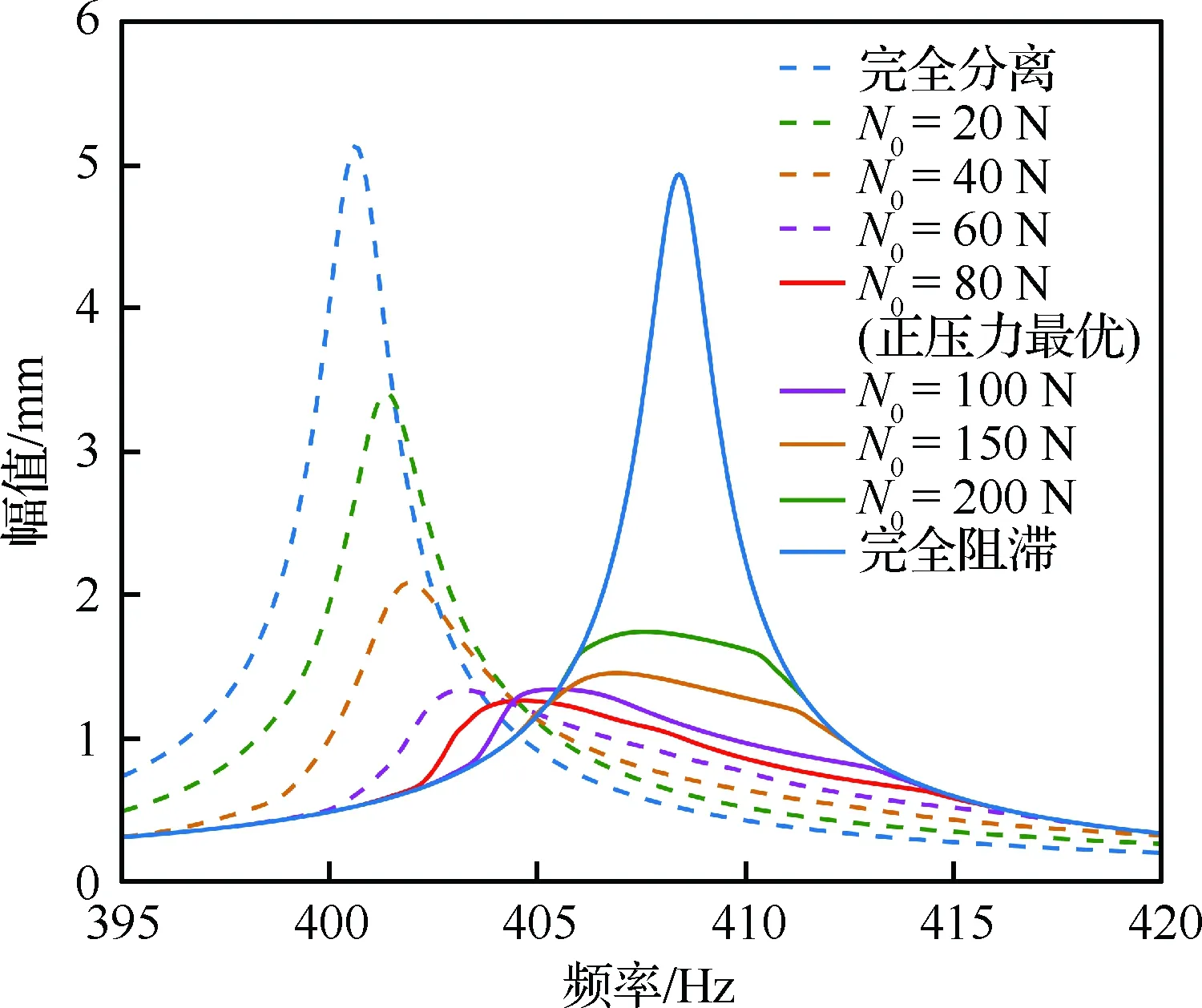
圖10 不同正壓力下的穩(wěn)態(tài)強迫響應結果
Fig.10 Steady state response of system under different normal preloads
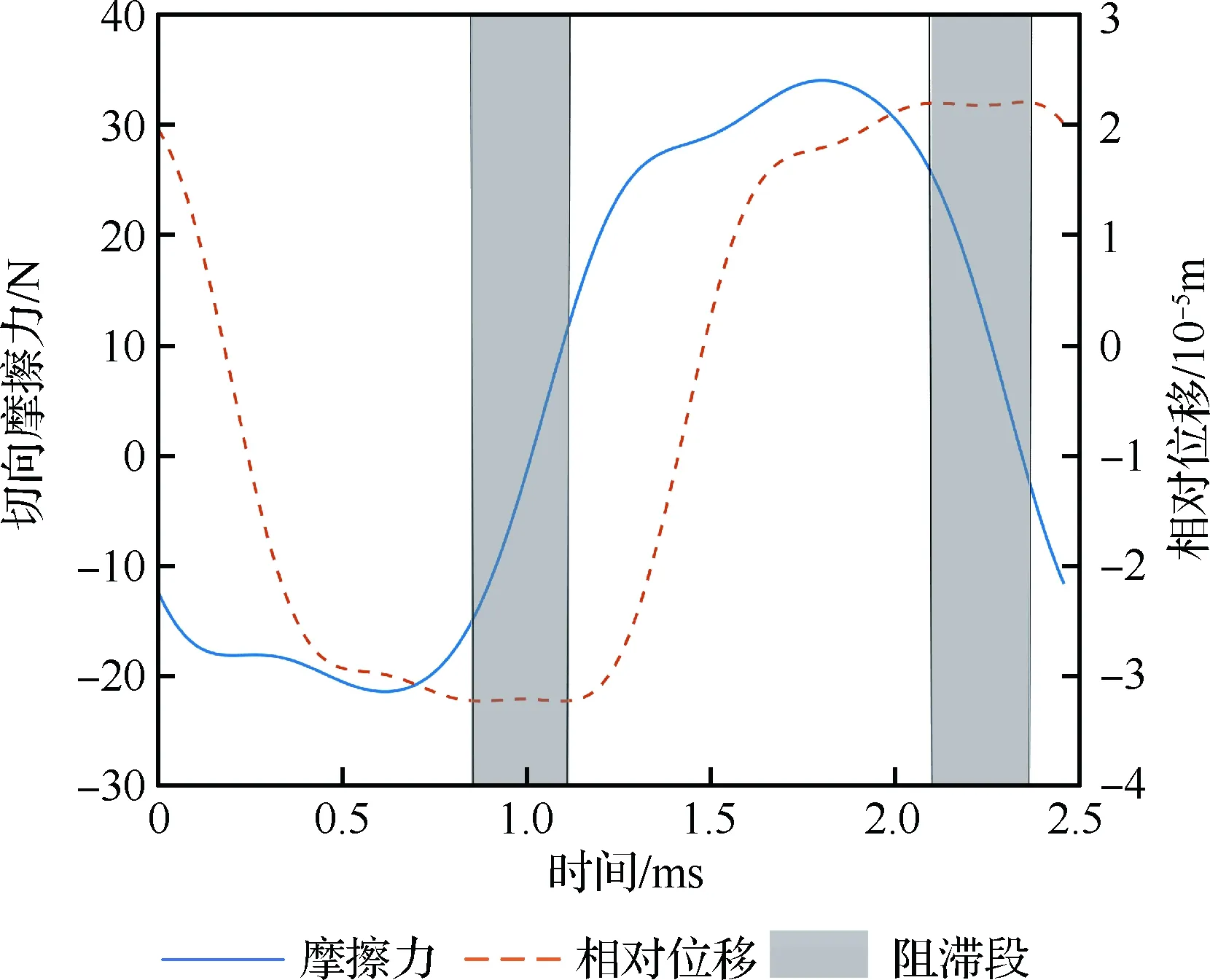
圖11 接觸點切向力和相對位移的時間歷程
Fig.11 Time-histories of tangential force and relative displacement for contact node
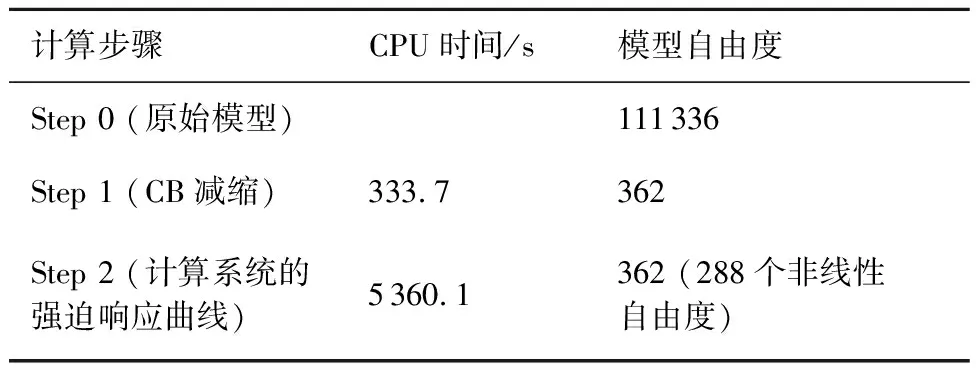
表3 計算時間與減縮過程中自由度數(shù)的變化
4 結 論
本文提出了一種適用于薄壁結構的波紋形干摩擦阻尼器,其具有結構簡單、附加質量小、易于安裝與調節(jié)初始正壓力的優(yōu)點。利用仿真模擬的手段對阻尼片的減振性能進行了分析,在高階諧波平衡法的基礎上引入了速度型動態(tài)拉格朗日法,并通過提供解析形式的雅克比矩陣來提高迭代效率與計算穩(wěn)定性,從而實現(xiàn)了對帶有接觸系統(tǒng)的頻域強迫響應的快速預測,之后的仿真過程表明該算法具有較高的計算效率。
利用強迫響應預測算法對帶有阻尼片的薄壁結構進行分析,可以看出,對于平板而言,通過合理布置阻尼片的位置,增大結構自由/阻滯時的頻率差,從而獲得較好的減振效果。以文中的平板結構為例,僅使用質量占整體結構0.6%的阻尼片就能使得共振峰值下降75.4%。
現(xiàn)有工作的一個展望是,針對干摩擦阻尼器在各頻段下最優(yōu)正壓力不同的特點,還可以引入主動控制環(huán)節(jié)通過設計可控正壓力提高干摩擦阻尼器在寬頻內的減振性能[30,39]。這些后續(xù)工作仍然需要一種可以考慮干摩擦界面切-法向耦合的高效數(shù)值工具,本文提出的基于減縮模型和解析雅克比矩陣的速度型動態(tài)拉格朗日乘子方法仍適用。
附錄A
布爾矩陣是元素只取0或1的矩陣,因此又被稱為0-1矩陣。它的作用是提取含有m個元素的向量X中的某些特定項,并將提取的元素重新組成維度為n的向量Y。該過程所對應的布爾矩陣B的維度為n×m。
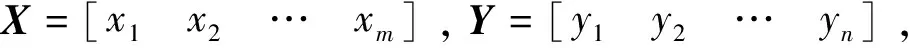
記R為X和Y上的對應關系,則布爾矩陣中B的各元素滿足:
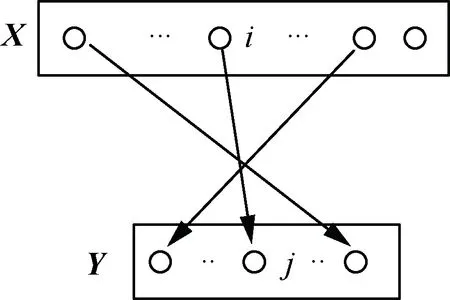
圖A1X與Y之間的對應關系
Fig.A1 Correspondences betweenXandY
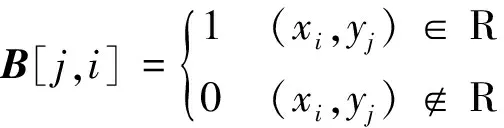
(A1)
其轉置矩陣BT則能將Y中的元素放回X中的對應位置。

