基于反向學習和高斯擾動的粒子群優化算法?

朱德剛 洪 建 張 潔

（安徽醫科大學第一附屬醫院 合肥 230022）

1 引言

粒子群優化（Particle Swarm Optimization，PSO）算法［1～2］是由 Kennedy和 Eberhart對動物的捕食行為觀察而得出。該算法流程簡單、具備一定的生物背景等優點，一經提出就得到無線傳感器［3］、函數優化［4］、神經網絡［5～6］等眾多領域的廣泛應用。

PSO算法相比較其他的智能優化算法具有很多優點，但隨著眾多學者的不斷研究，發現傳統的粒子群優化算法在收斂速度和陷入局部最優方面存在缺陷。大量學者針對粒子群算法這個缺點，進行了大量的算法改進，不斷地提高算法的收斂速度和精度。Liang等通過改變傳統PSO算法的拓撲結構，采用動態的鄰域拓撲結構，提出了綜合學習粒子群優化算法［7］；林國漢等根據種群的多樣性，動態分配種群中粒子任務，將種群進化分為多個狀態，采用不同的模型來平衡算法的全局和局部搜索能力，提出了自適應任務分配的粒子群優化算法［8］。Zhan等通過對種群的進化的過程進行研究，將其劃分為四個進化狀態，算法的相關參數可以自適應的根據當前算法狀態進行調整，提出了自適應子空間高斯學習的粒子群優化算法［9］。文獻［10］提出了協同粒子群優化算法，算法將PSO算法劃分成多個子群，每個子群對解向量各個部分進行優化，引入協同進化思想，各個子群協同進化。朱德剛等通過對粒子當前的歷史最優位置增加高斯擾動項，提出一種基于高斯擾動的粒子群優化算法［11］。孫輝等通過構造一種新的子群信息共享模式，并對粒子進行子空間學習，提出一種多種群子空間學習的粒子群優化算法［12］。

如何采用有效的策略解決標準粒子群優化算法的缺陷，成為了眾多學者研究的重要方向之一。本文提出以一種基于反向學習和高斯擾動的粒子群優化算法（OGPSO）。算法在傳統的PSO“自我認知”和“社會學習”基礎上，隨機選擇種群中任意粒子的反向位置，該反向位置引導當前粒子進行運動，在進化過程中，對種群最優粒子進行高斯擾動，增加算法找到最優解的概率。在經典測試函數上，本文算法相比較其他知名算法具有更好的收斂速度和精度。

2 標準粒子群算法

PSO算法可看做一個種群大小為N的粒子群在問題維度為D的范圍內進行搜索，第i(i=1，2，…，N)個粒子在第t次迭代時位置和速度分別為粒子i在第t+1次迭代時第d(d=1，2，…，D)維子空間的速度和位置根據下式調整。

式中：w為慣性權重；c1和c2為加速因子；r1、r2是在（0，1）之間的隨機數；分別為粒子i在第t次迭代時歷史最優位置和種群最優位置。

3 OGPSO算法

3.1 反向學習策略

反向學習策略（Opposition-based Learning，OBL）［13］主要指種群在進化過程中，每個粒子每次找到一個當前最優位置時均產生一個對應的反向位置，如果反向位置的適應值較優，將其作為當前粒子的最優位置。

定義1普通反向學習（Generalized Opposi?tion-based Learning，GOBL）。設當前粒子的最優位置xi(t)在其反向位置第 j維上可定義為

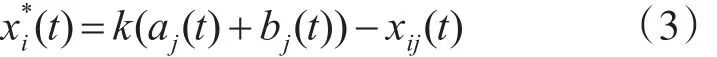
定義2改進的反向學習（Improved Opposi?tion-based Learning，IOBL）。設 Xi(t)=(xi1，xi2，…，xiD)為種群中第i個粒子在第t代時的位置，則對應的反向粒子位置 X?i(t)=(x?i1，x?i2，…，x?iD)可定義為

其中 xij∈[aj，bj]，k 、k1和 k2屬于（0，1）之間隨機數，[aj，bj]為xij第 j維的區間，具體表示如下：

如果反向解 xij?[aj，bj]，則按式（6）更新：

3.2 算法進化公式

在標準PSO算法中，粒子的運動方向主要由粒子的歷史最優位置 pij和全局最優位置 pgd來決定。OGPSO算法為了增加種群多樣性，粒子的運動方向由 pij、x?kj、Ggd和 pgd共同決定，隨機選擇種群中的任一粒子的反向粒子作為當前粒子的引導粒子，擴大了算法尋優范圍，幫助算法快速找到全局最優位置。具體的進化模式如下所示。

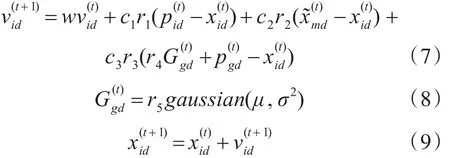
其中 m=rand(1，2，…，i，…N)，N為種群粒子數目，w為慣性權重，c1、c2和c3為加速因子，r1、r2、r3、r4和 r5均在（0，1）區間，和為粒子i在第t次迭代時的速度和歷史最優位置，是第t次迭代時隨機選擇的第m個粒子的反向粒子位置，是第t次迭代時整個種群的最優位置，表示第t次迭代時種群最優粒子的高斯擾動粒子。μ表示均值，σ2表示方差。

3.3 算法流程圖

算法的具體步驟如圖1所示。

4 仿真實驗

4.1 基準測試函數

本 文 通 過 比 較 FIPS［14］、HPSO-TVAC［15］、DMS-PSO［16］、CLPSO［7］和 APSO［9］五種經典算法性能，選擇了八種較經典的測試函數。測試函數的函數形式、搜索范圍和理論最優值如表1所示。

圖1 算法流程圖

4.2 算法的參數設置

種群粒子數目N=10，評估次數T=200000，慣性權重 w=0.8?e(-0.5?t/iterNum)為慣性權重，t表示當前的迭代次數，iterNum表示總的迭代次數，均值 μ=0 ，方 差 σ2=|，表示方差學習因子c1=1.5，c2=0.5，c3=2.0。

4.3 仿真實驗結果

4.3.1 低維仿真實驗結果

表2中的Mean和Std.Dev表示最優適應值的均值和標準差。選取四個單峰函數 f1、f2、f3、f4和四個多峰函數 f5、f6、f7、f8，以獨立運行30次的平均值作為算法最終的解。

由表2可知，OGPSO算法相比較其他5種知名算法，不僅在單峰函數上優勢明顯，而且在多峰函數上依然保持絕對優勢。特別在單峰函數 f1、f2和多峰函數 f5、f6和 f8，達到了最優值0。

表1 8種測試函數

為了更好地表現OGPSO在算法進化過程中的收斂情況，本文將OGPSO和其他五種算法在8個30維測試函數上進化過程中適應值收斂情況進行比較。觀察圖2～圖9可知，本文算法中的反向粒子和高斯擾動粒子能夠加快收斂速度，提高算法精度。通過圖2～圖5可知，OGPSO算法在處理單峰函數時，收斂速度和精度優勢明顯，特別是 f1、f2函數，進化到6～8萬次就已經尋找到全局最優位置。觀察圖6～圖9可知，OGPSO算法能夠幫助多峰函數逃離其局部最優，加快算法的收斂速度，特別是在 f5、f6、f8函數表現很好，算法的收斂速度非常快，且能夠快速找到全局最優位置。

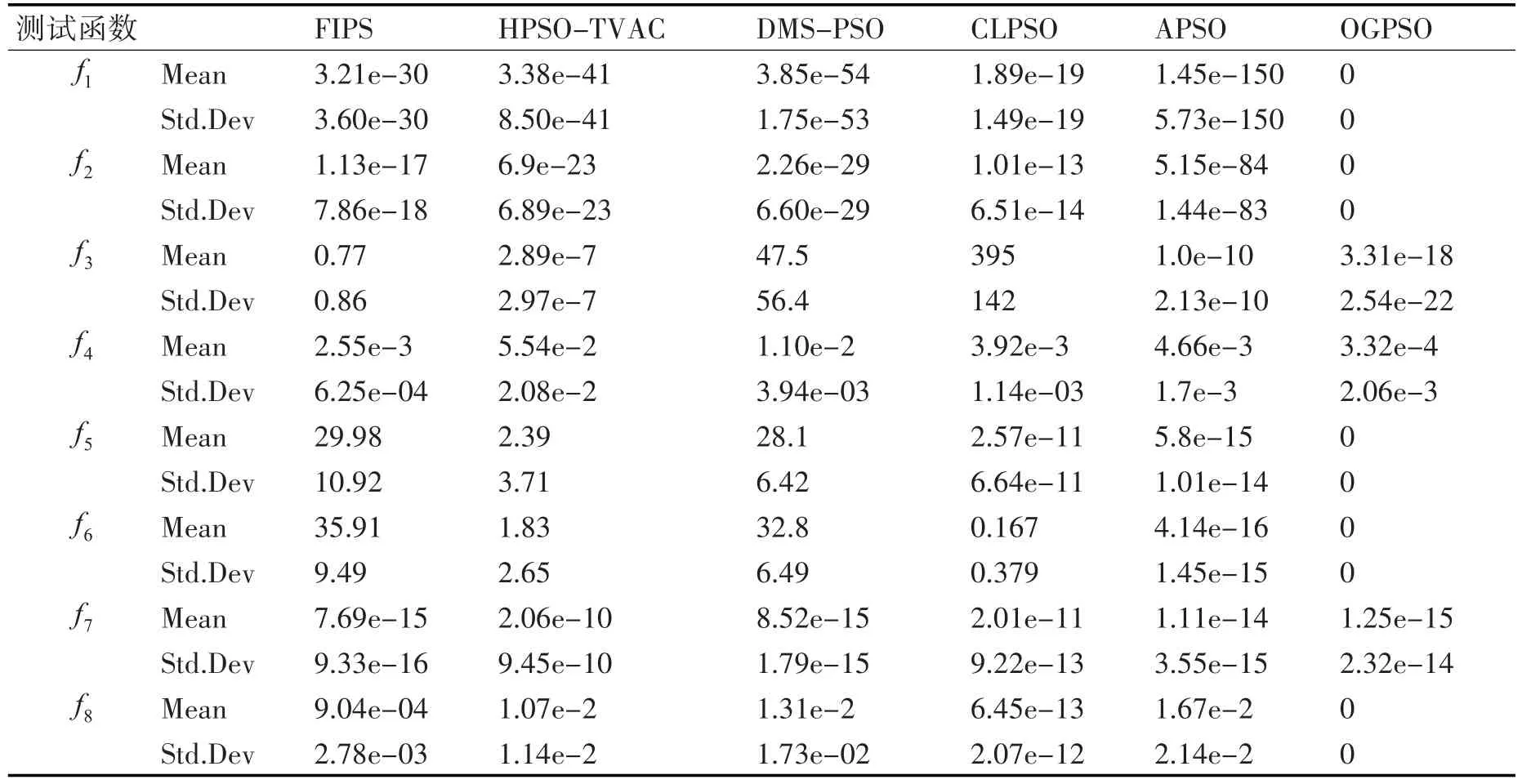
表2 六種算法在30維問題上的比較

圖2 f1函數進化過程曲線圖

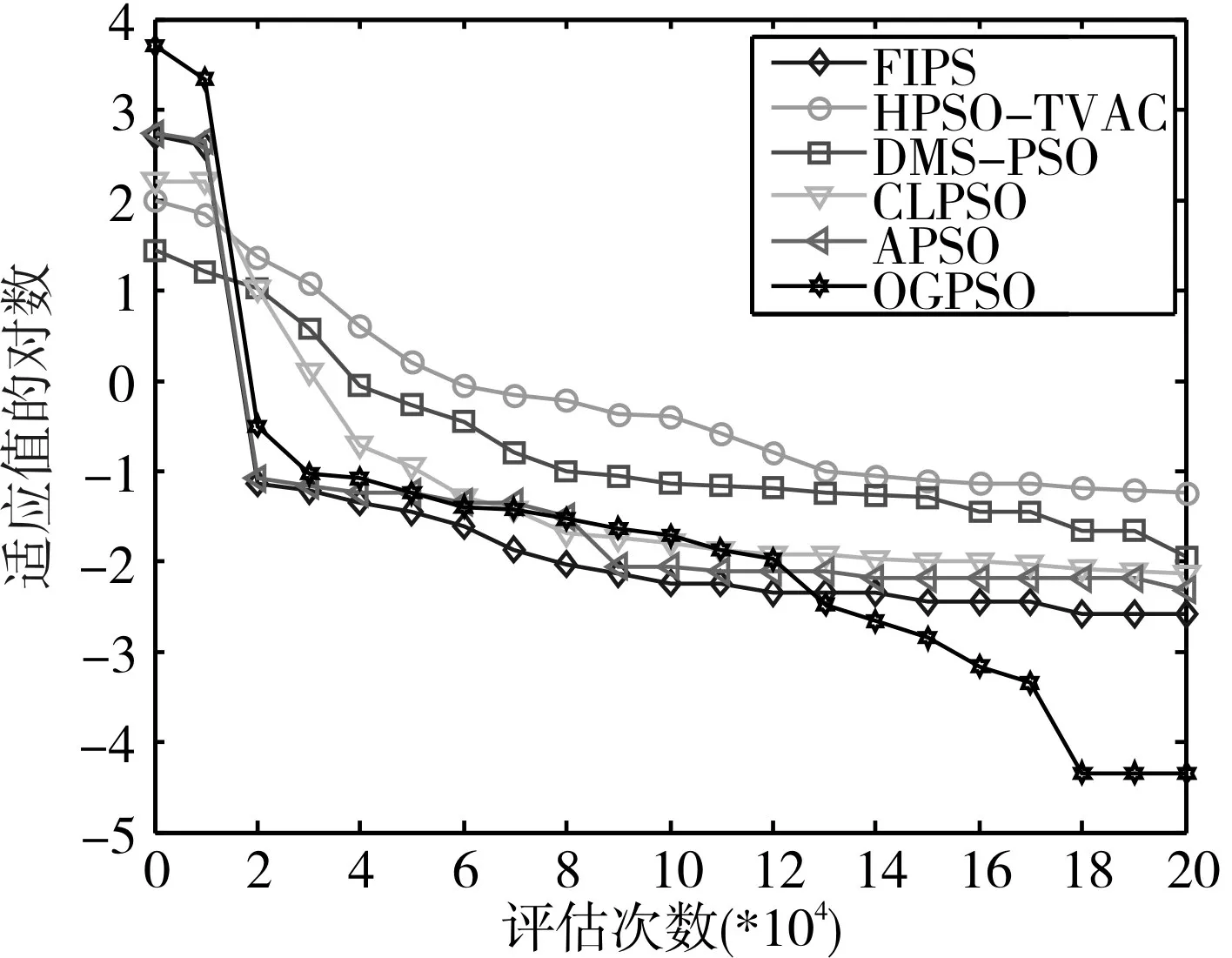
圖5 f4函數進化過程曲線圖

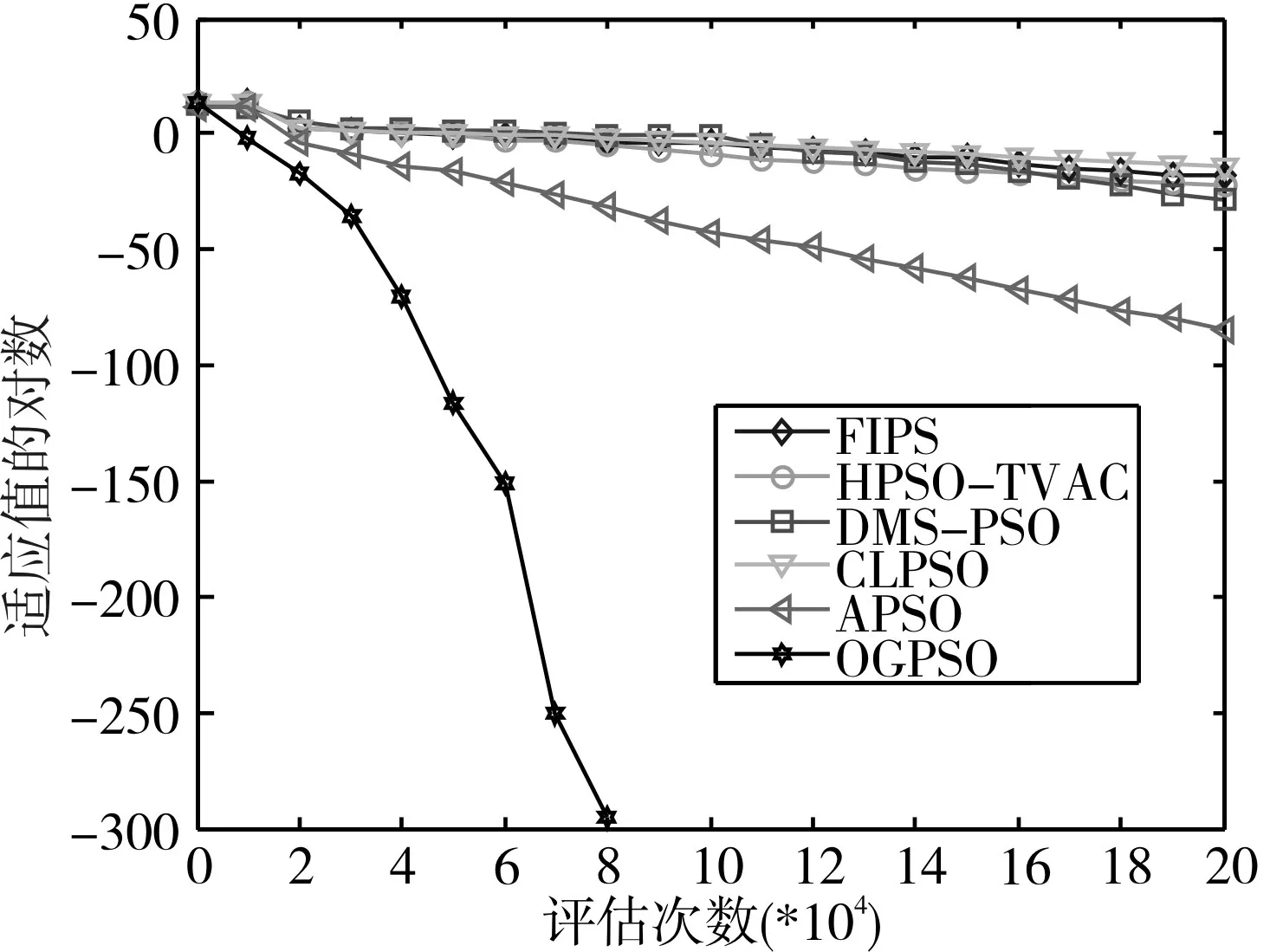
圖3 f2函數進化過程曲線圖

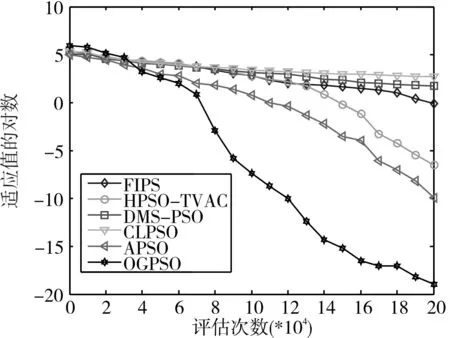
圖4 f3函數進化過程曲線圖

圖6 f5函數進化過程曲線圖

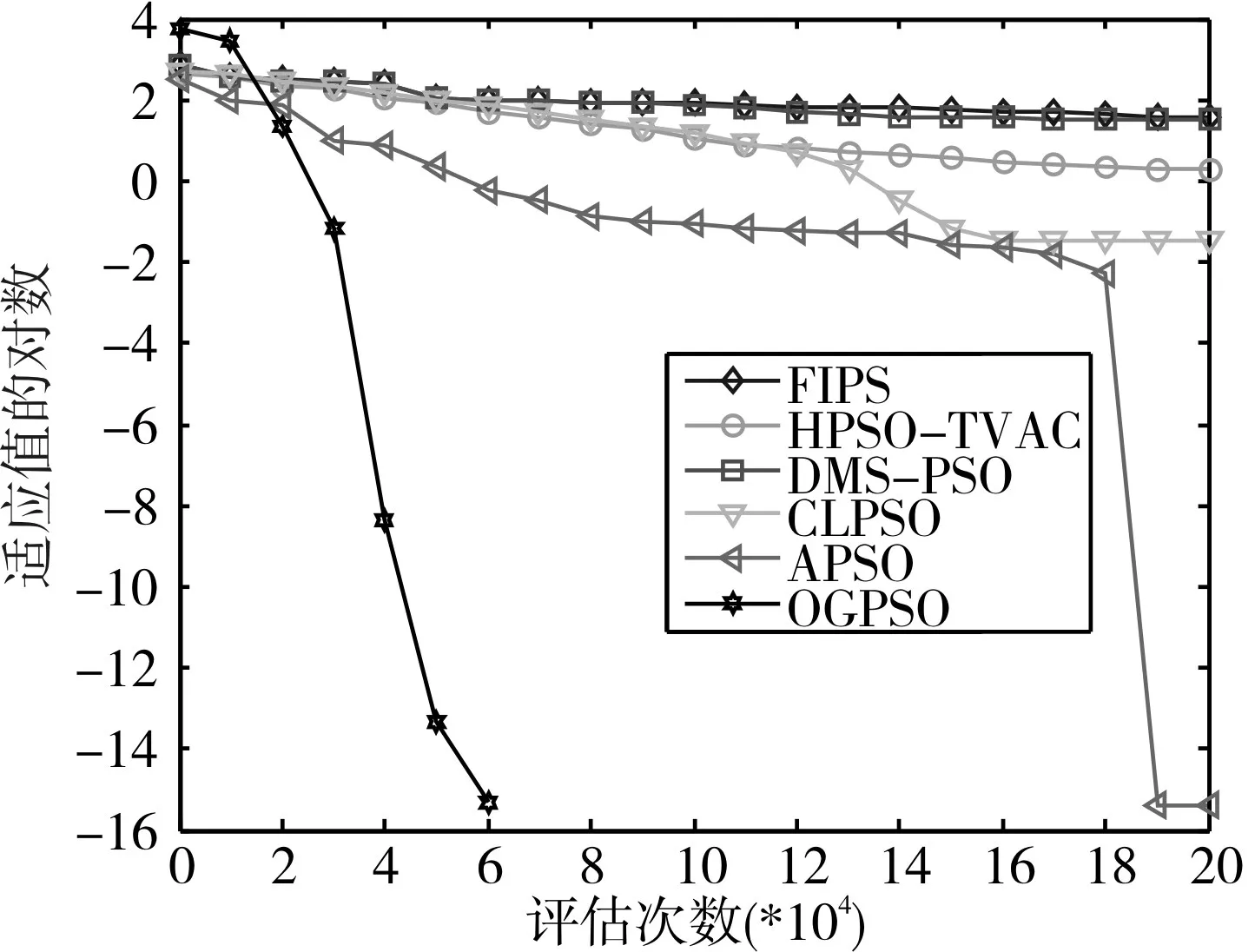
圖7 f6函數進化過程曲線圖

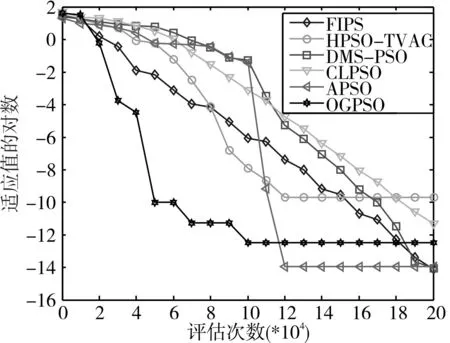
圖8 f7函數進化過程曲線圖

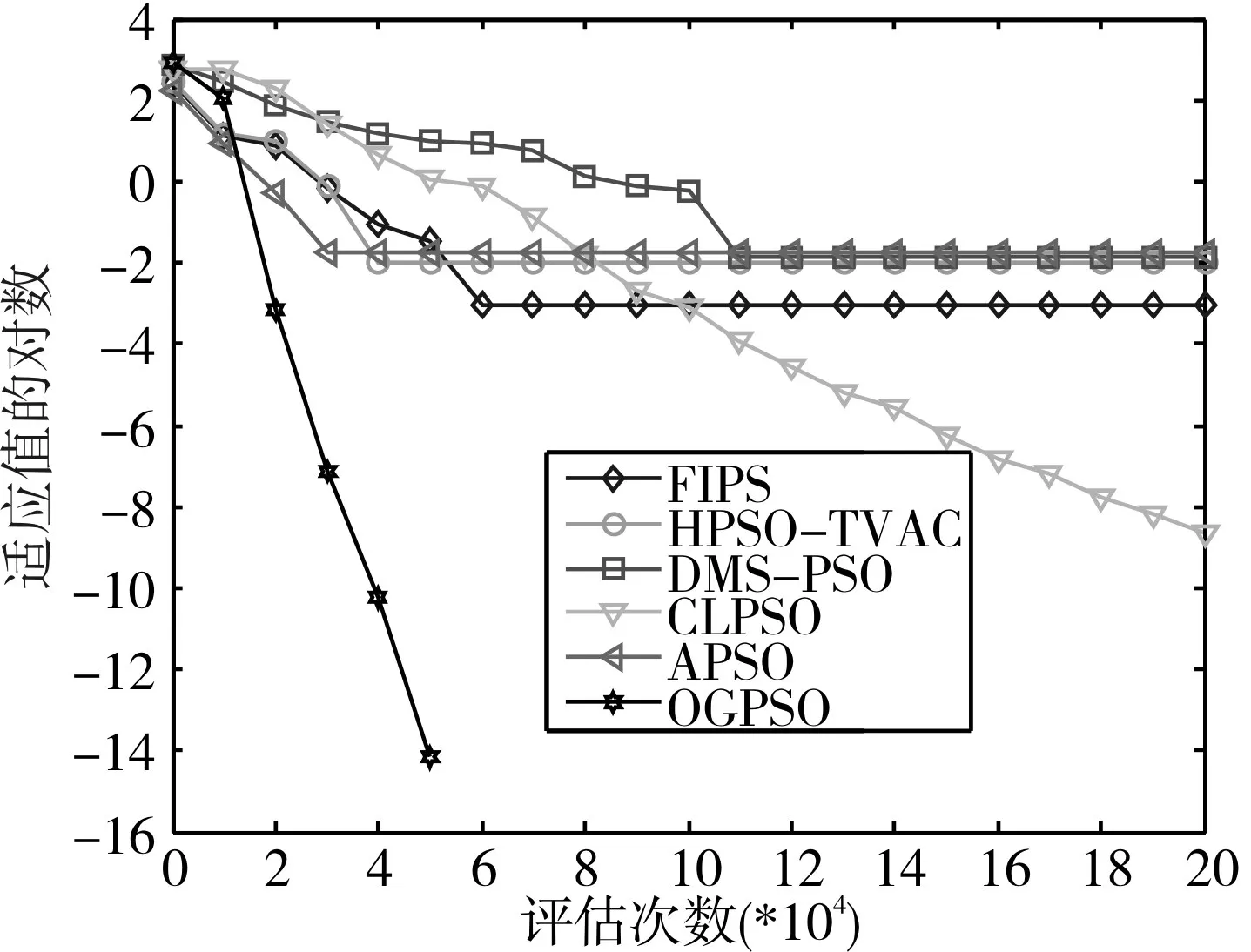
圖9 f8函數進化過程曲線圖

4.3.2 高維仿真實驗結果

為了驗證MSPSO算法的優越性，選擇PSO算法和CLPSO算法進行對比測試。粒子個數為20，評估次數為D*5000次，D為函數維數。算法的測試結果如表3所示。表中結果均為30次獨立運行的平均值。

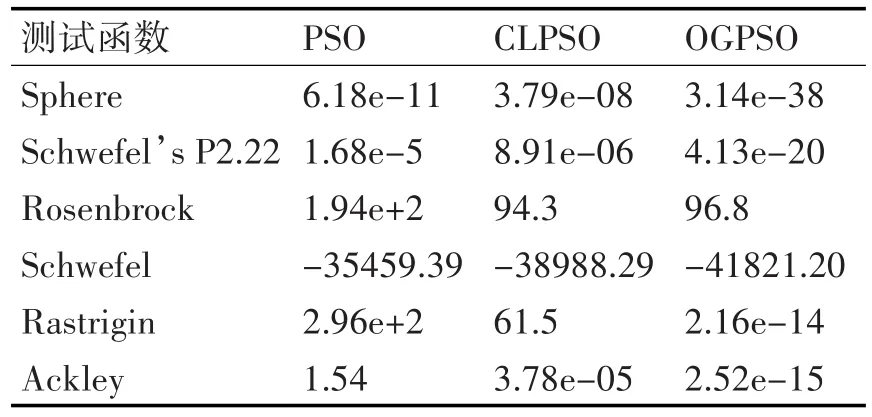
表3 改進算法的測試結果

由表3可知，函數維數為100維時，OGPSO算法除了在Rosenbrock函數的測試結果上稍差于CLPSO算法，在其它六種函數上均優勢明顯。

5 結語

為了研究標準PSO算法的特點，針對其缺點，本文算法提高了標準PSO算法收斂速度和精度，避免算法過早陷入局部最優。通過增加反向粒子和高斯擾動項，增加種群多樣性，提高尋優的概率，幫助算法逃離局部最優位置。實驗表明，通過對低維和高維的經典函數進行比較，OGPSO算法相比較其他幾種算法收斂速度更快、精度更高。函數進化過程曲線圖進一步說明了本文算法的收斂速度具有很大的優勢，收斂精度更高。