一種改進的ID3決策算法及其應用?

圣文順 孫艷文

（南京工業大學浦江學院 南京 211222）

1 引言

決策樹分類方法是一種有效的實例學習［1］和數據挖掘［2］方法，當前最有效的決策樹分類算法是Quinlan在1986年提出的ID3算法，其中決策樹以自頂向下遞歸的分治方式構造［3］。ID3算法的思想是將所有實例（或者數據庫中的數據）作為決策樹的根節點，按照信息論方法中熵［4］的概念來度量各項屬性的信息度，以此作為選擇屬性的依據，根據屬性值對樹根進行分裂，建立分支節點；然后將每個分支節點分別作為根節點，重復進行“選擇屬性——分裂樹”的操作，直到最后的分支節點僅包含正例或者反例，構建成一棵完整的決策樹［5］。

2 ID3算法理論

對于有大量實例數據的歸納學習，常采用ID3算法。實例數據［6］一般都是混亂無序的，歸納學習［7］的目的就是從無序的數據中找出內在蘊涵的規律。實例數據一般都基于屬性理論，這樣就允許使用信息論方法來測試特定屬性值從而進行分類。ID3算法的核心思想是將Shannon的信息論方法［8］引入到屬性選擇中。ID3算法通過把每個屬性當作當前子樹的根節點來度量信息增益［9］。

Shannon的信息論方法提供了度量一條信息的信息量的數學基礎。將一條信息看成是可能信息空間的一個實例；傳播信息的動作就相當于從可能的信息中挑選出一個。從這個觀點來看，定義一條信息的信息含量依賴于這個空間的大小、每個可能的信息的出現頻率。對于實例學習，可將每一實例的屬性看作一條信息，屬性的選擇即可從屬性的信息量出發，優先選擇信息量高的屬性生成決策樹。

ID3算法中信息論方法形式化如下：設作為訓練集的實例數據集合為X，ID3學習的過程是將該實例數據集合根據某一屬性A的屬性值分為n類，記為{c1，c2，…，cn}，第i類的實例數據的個數計為|Xi|，—個實例數據屬于第i類的概率為p(Xi|A=ai)，則有：

概率p(Xi|A=ai)即為屬性A的屬性值等于ai的概率。給定屬性取值空間和每一屬性值出現的概率，那么可定義該屬性值的信息含量數學期望值：

對于實例集X，最終會將其分為n類，設為{c1，c2，…，cn} ，則有決策樹劃分X的信息量為

選擇屬性A后，對劃分出的每個子集，可得：

根據信息論方法，在當前樹的根節點做測試所提供的信息增益與樹的總的信息量減去測試完成后完成分類索溪的信息量相等，則有：

式（5）即為屬性A的信息增益，信息增益越大，說明選擇該屬性進行決策樹的劃分帶來的不確定性越小，越能快速的構建好決策樹。ID3算法基采用Gain(A)［10］作為選擇測試屬性的依據生成決策樹。

3 ID3算法改進

由ID3算法可知，信息增益最大要求I［X］值盡量大。研究表明，采用加權和計算［11］的選擇方式往往傾向于選擇取值較多的屬性，而拋棄取值少的屬性。然而在實際中，取值多的屬性并不一定是主要屬性，取值少的屬性不一定是非主要屬性，這種屬性稱為噪聲［12］。現提出對ID3算法進行改進——對每項屬性的權重加以修正，在選擇測試屬性時，不再以屬性的取值多少作為主要依據。

設修正權值［13］為a，取值區間為［0，1］，該權值由用戶根據先驗知識確定。先驗知識［14］是指先于經驗的知識，具體包括領域知識和專家建議。先驗知識調節其對分類的信息量，提高分類的準確性，應用到決策樹學習中，除了用于生成和修改決策樹的實例集之外，還包括所有影響決策樹規則生成和選擇的因素。先驗知識是一個模糊概念，可使用模糊集概念［15］來輔助確定。

改進的ID3算法主要步驟如下：在式（4）中加入α，可得：

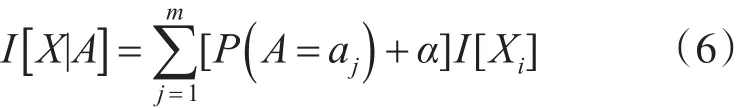
相應的增益為

改進的算法使用式（6）和式（7）來代替原式生成決策樹。

4 算法驗證

本文通過分析HR選擇就職人員的記錄，應用改進后的ID3算法生成符合就職的決策規則。示例樣本數據見表1。

表1 樣本數據

對于覆蓋所有歷史樣本數據的樹的信息含量為

假設選擇歷史樣本數據的屬性“專業”作為決策樹的根節點，可將歷史樣本數據分為C1=｛1，14｝、C2=｛2，4，5，8，10，11，13，15｝和 C3=｛3，6，7，9，12｝，分別對應“專業”屬性取值為“國際貿易”、“通信與信息系統”和“計算機科學與技術”的取值分類。根據先驗知識，對性別、年齡、學歷、專業分別設修正權值為0.3、0.2、0.1、0。完成樹所需的信息量數學期望為

即選擇專業屬性測試的信息增益為0.304。

類似可得：

對應所得的決策樹為

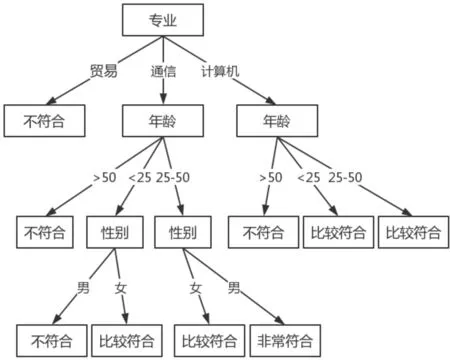
圖1 決策樹

5 結語

上述算法示例表明，在原有ID3算法中加入屬性修正權值，同樣能夠生成決策樹，且具有可行性。加入修正權之后，ID3決策樹的生成不再僅僅依賴于屬性的信息量，先驗知識也能夠對決策樹的生成起到影響，可以對算法中噪聲的產生起到抑制作用。

先驗知識的獲得和表示是該改進算法的重要部分，如何確定屬性修訂權值直接影響了改進算法的效果。先驗知識的處理屬于模糊集合問題，可用粗糙集概念［16］對其進行形式化描述，已有不少學者在這方面進行深入研究，這也是下一步研究工作的重點。