例談學(xué)生數(shù)學(xué)邏輯推理能力的培養(yǎng)
——以“相似三角形的應(yīng)用1”的教學(xué)為例

■朱加軍

（作者單位：江蘇省江陰市峭岐中學(xué)）

在小學(xué)數(shù)學(xué)階段，學(xué)生對(duì)邏輯推理的經(jīng)歷主要是以直觀猜想為主的規(guī)律探尋，是“經(jīng)驗(yàn)型”思維，缺少理論支撐，邏輯性不強(qiáng)。初中數(shù)學(xué)“公理”“定理”“概念”等知識(shí)增多，學(xué)生隨著年齡的增長(zhǎng)和認(rèn)知水平的發(fā)展，要逐漸過渡到“理論型”邏輯推理階段。因此，初中數(shù)學(xué)教師在課堂教學(xué)中，要根據(jù)學(xué)生學(xué)習(xí)數(shù)學(xué)的邏輯障礙，有針對(duì)性地、循序漸進(jìn)地促進(jìn)他們邏輯思維的發(fā)展，有效培養(yǎng)他們的邏輯推理能力，這也是初中數(shù)學(xué)教學(xué)的重、難點(diǎn)。本文根據(jù)數(shù)學(xué)核心素養(yǎng)的要求，結(jié)合蘇科版九年級(jí)《數(shù)學(xué)》“相似三角形的應(yīng)用1”的教學(xué)片段，試從以下四個(gè)方面談一談?wù)n堂中學(xué)生邏輯推理能力的培養(yǎng)。

一、預(yù)設(shè)情境，激發(fā)興趣，推動(dòng)邏輯推理能力的發(fā)展

“樂學(xué)”是核心素養(yǎng)提出的學(xué)會(huì)學(xué)習(xí)中的一個(gè)要求，也是學(xué)生學(xué)習(xí)數(shù)學(xué)過程中最為重要的數(shù)學(xué)素養(yǎng)。學(xué)生邏輯推理能力的發(fā)展，更加需要一個(gè)興趣盎然的環(huán)境。因此教師教學(xué)時(shí)，要精心設(shè)計(jì)一個(gè)富有生活趣味的、能引起學(xué)生關(guān)注并希望深入了解的問題，使學(xué)生樂于思索，從而推動(dòng)其邏輯推理能力的發(fā)展。

在“相似三角形的應(yīng)用1”課堂伊始，教師便拋出一個(gè)問題：

在某一個(gè)晴天，你手中只有最大測(cè)量長(zhǎng)度為20米的卷尺。請(qǐng)問，你如何測(cè)量一個(gè)12層居民樓的高度？說說你的方案。

生1：可以先量一層樓的高度，再乘樓層數(shù)。

生2：不可以，因?yàn)闃菍痈叨炔⒉煌耆嗤^大多數(shù)的樓是一樓的層高較高，況且還有頂樓的高度無(wú)法測(cè)量。此方案行不通。

生3：可以先立一根木桿，然后退到適當(dāng)位置，當(dāng)看到木桿的頂端與樓頂重合時(shí)，就可以運(yùn)用我們學(xué)過的相似三角形的知識(shí)解決了。示意圖如圖1。

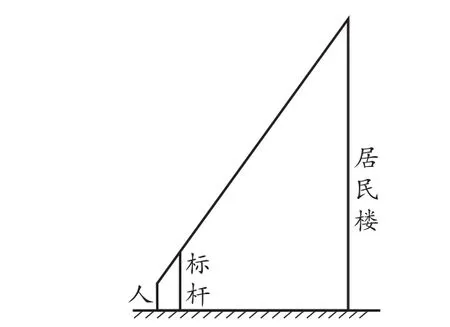
圖1

師：生3的方案的確不錯(cuò)，具有了操作性，也能測(cè)出相對(duì)準(zhǔn)確的高度，這是我們以前學(xué)習(xí)的方案。但假如沒有木桿，你能利用現(xiàn)有的工具來(lái)測(cè)量嗎？不要忘了天氣是晴，所有的物體在太陽(yáng)下都會(huì)有影子。

生4：可以先測(cè)出一個(gè)人及其影子的高度，再測(cè)出大樓的影子長(zhǎng)，然后利用比例，就可以求出樓高了。

到此，問題解決。此問設(shè)計(jì)的目的是活躍課堂氣氛，提升學(xué)生思考的欲望，增加學(xué)生學(xué)習(xí)新課的興趣。學(xué)生積極思考問題，會(huì)想出多種方案，但方案提出后需要運(yùn)用邏輯推理來(lái)驗(yàn)證方案的可行性與可操作性。實(shí)際上從問題提出，到疑問產(chǎn)生，到方案產(chǎn)生，到驗(yàn)證方案的可行性，再到答案的給出，就是一個(gè)基本的邏輯推理過程，也是一個(gè)激發(fā)學(xué)生興趣、培養(yǎng)學(xué)生樂學(xué)素養(yǎng)的過程。

二、厘清概念，完善問題，培養(yǎng)邏輯推理的嚴(yán)密性

面對(duì)數(shù)學(xué)問題，進(jìn)行邏輯推理時(shí)，會(huì)涉及眾多的數(shù)學(xué)概念。厘清概念是數(shù)學(xué)邏輯的基礎(chǔ)，也是邏輯推理正確發(fā)展的保障。為此，課堂上教師進(jìn)一步提出更完整的數(shù)學(xué)問題。

師：如圖2，在某晴天的某一時(shí)刻，一個(gè)身高1.8米的學(xué)生在太陽(yáng)下的影子長(zhǎng)是0.6米，同一時(shí)刻，某一大樓的影子長(zhǎng)是12米。你能計(jì)算出此大樓的高嗎？

圖2

師：此題中，生4的比例式如何得出？

生5：可以依據(jù)相似三角形的性質(zhì)得出。

師：你能說說哪兩個(gè)三角形相似嗎？

生5：大樓與自己的影子構(gòu)成了一個(gè)直角三角形，人與自己的影子也構(gòu)成了一個(gè)直角三角形。這兩個(gè)直角三角形相似。

師：如果真如你所說的相似，那么它們的相似條件是什么？

生5：太陽(yáng)的光線是平行的，因此它們與地面構(gòu)成的角是相等的，大樓、人與地面都是垂直的，因此它們與地面形成的角都是直角。這樣，這兩個(gè)直角三角形兩組角相等，所以兩個(gè)三角形相似。

本節(jié)課是一節(jié)數(shù)學(xué)知識(shí)技能的運(yùn)用課，所涉及的知識(shí)基本都是數(shù)學(xué)方法的運(yùn)用，要求掌握的新的數(shù)學(xué)概念基本沒有，但在解決問題的過程中，仍然需要強(qiáng)化所涉及的一些概念。比如此問題中，對(duì)于“同一地點(diǎn)下的陽(yáng)光是平行光”這一物理知識(shí)中的概念需要再次明確；人、大樓分別與水平地面是垂直的。這些基本概念是保證樓高、樓影長(zhǎng)構(gòu)成的直角三角形與人高、人影長(zhǎng)構(gòu)成的直角三角形相似的關(guān)鍵，也是進(jìn)行下一步邏輯推理計(jì)算的保證。這是從小學(xué)直觀的邏輯推理，走向初中嚴(yán)密的邏輯推理的關(guān)鍵過程，是培養(yǎng)學(xué)生“有實(shí)證意識(shí)和嚴(yán)謹(jǐn)?shù)那笾獞B(tài)度”的良好方法。

三、構(gòu)建數(shù)學(xué)模型，培養(yǎng)抽象能力

學(xué)生的核心素養(yǎng)要求中提出，要能運(yùn)用科學(xué)的思維方式認(rèn)識(shí)事物、解決問題、指導(dǎo)行為。構(gòu)建數(shù)學(xué)模型是一個(gè)非常有效的思維方式，也是促進(jìn)邏輯推理能力發(fā)展的快速有效的良好方法。將上題抽象成數(shù)學(xué)問題，是學(xué)生將新知轉(zhuǎn)化為舊知，將實(shí)際問題歸納為數(shù)學(xué)問題的關(guān)鍵。

生6：可以將實(shí)物圖轉(zhuǎn)化成圖3，在Rt△ABC與Rt△DEF中，邊AB表示大樓，邊CB表示大樓的影子，邊DE表示人高，邊EF表示人的影子。

生7：雖然生6的圖3可以解決此題，但仍然不夠簡(jiǎn)潔。我們知道，大樓不可以移動(dòng)，但是人可以移動(dòng)，同時(shí)轉(zhuǎn)換視角，就可以將人與大樓重疊到一起，如圖4，兩個(gè)三角形的相似就可以相對(duì)容易得出，比例也相對(duì)容易得出。

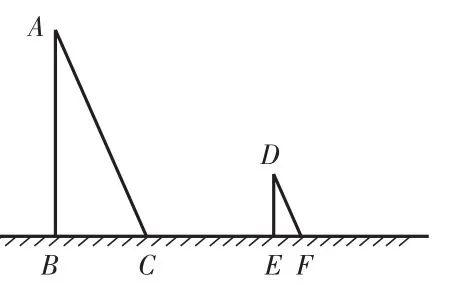
圖3

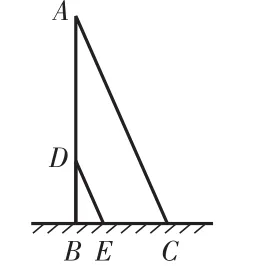
圖4

不難看出，生7構(gòu)建的數(shù)學(xué)模型更為簡(jiǎn)潔、有效，也更能直觀表現(xiàn)出物高與影長(zhǎng)的比例關(guān)系。因此，建立一個(gè)簡(jiǎn)潔、有效的數(shù)學(xué)模型，在邏輯推理過程中可以簡(jiǎn)化思維過程，明晰邏輯推理思維的方向。所以在課堂教學(xué)中教師應(yīng)當(dāng)善于引導(dǎo)學(xué)生建立簡(jiǎn)潔、有效的數(shù)學(xué)模型，讓學(xué)生從問題的感知升華為思維的感知，最終形成一定的思維模式，歸結(jié)為一定的數(shù)學(xué)模型，讓學(xué)生的思維層次進(jìn)一步提高，為推理積累感性的經(jīng)驗(yàn)。數(shù)學(xué)中很多的邏輯證明的方法，如分析法、反證法、類比法、歸納法等都是按照邏輯推理的規(guī)律進(jìn)行的一種數(shù)學(xué)活動(dòng)，有利于邏輯思維能力的發(fā)展。

四、規(guī)范說理過程，彰顯數(shù)學(xué)素養(yǎng)

語(yǔ)言的源泉是理性思維，也是邏輯推理的過程呈現(xiàn)。邏輯推理過程的學(xué)習(xí)一定程度上也可以說成是數(shù)學(xué)語(yǔ)言的推理過程。教學(xué)中，要鼓勵(lì)學(xué)生在自己獨(dú)立思考的基礎(chǔ)上與同學(xué)、教師交流，以此來(lái)促進(jìn)邏輯推理思維的成熟，讓推理更嚴(yán)密。教師在教學(xué)中應(yīng)當(dāng)適時(shí)管控推理的進(jìn)程，規(guī)范說理的策略，逐漸形成“條件A+條件B+條件C+…=＞結(jié)論”的形式，多引導(dǎo)學(xué)生質(zhì)疑、糾錯(cuò)，幫助學(xué)生將邏輯推理內(nèi)化成一種本能。如：

師：同學(xué)們，能否就圖3說一說比例式成立的理由？

師：在生8的答題過程中有沒有欠缺的地方？

生9：生8沒有將兩個(gè)三角形相似的理由說清楚。我可以將這部分補(bǔ)充完整，補(bǔ)充如下：

根據(jù)題意得：AB⊥BC，DE⊥EF，AC∥DF，∴∠ABC=∠DEF=90°，∠ACB=∠DFE，∴Rt△ABC∽R(shí)t△DEF。

師：生9補(bǔ)充得很好。在邏輯推理的過程中，我們應(yīng)當(dāng)注重?cái)?shù)學(xué)語(yǔ)言的表述，同時(shí)也要注重邏輯推理的完整性、嚴(yán)密性。在生8與生9的共同努力下，此題的解答過程就完整了。

數(shù)學(xué)是一個(gè)完整而又嚴(yán)密的體系，有獨(dú)有的符號(hào)作為科學(xué)的語(yǔ)言對(duì)邏輯推理過程進(jìn)行表述。數(shù)學(xué)課堂中對(duì)一些問題的解答、證明過程，用數(shù)學(xué)語(yǔ)言嚴(yán)謹(jǐn)?shù)赝评恚褪且粋€(gè)邏輯思維活動(dòng)的過程。因此，提高學(xué)生運(yùn)用數(shù)學(xué)語(yǔ)言的能力，可以提高學(xué)生的數(shù)學(xué)素養(yǎng)。