電動公交車線路和充電設施及策略規劃方法研究

姜嵐清，張勇

(蘇州大學 軌道交通學院，江蘇 蘇州 215131)

電動汽車替代傳統燃油汽車已成為汽車產業可持續發展的必然趨勢，也是解決能源消耗與環境污染問題的有效手段。電動公交車具有固定的行駛路線、發車時間以及停車場所，能夠很好地適應電動汽車續航里程短、充電時間長的特點，使得電動公交車成為電動汽車在中國市場推廣的先驅。在國家的大力支持和推動下，我國電動公交事業進入快速發展時期，2015年交通部出臺的《關于加快推進新能源汽車在交通運輸行業推廣應用的實施意見》，指出到2020年城市新能源公交車將達到20萬輛[1]。目前，國內主要城市新能源公交車占比都已達到40%以上，其中深圳在2017年已實現公交100%車電動化，根據各地規劃要求，到2020年全國公交車電動化率有望達到70%。由于電動公交車與汽油車補能方式不同，時間差別大，因此要求電動公交線路設計時要考慮充電樁配置要求。但是從目前各地市電動公交車充電設施建設情況來看，由于多依賴經驗配置、缺乏理論指導，充電樁配置數量相差較大，有的按照“一車一樁”配置，有的按照“四車一樁”配置，有的按照“六車一樁”配置，造成車樁配置不合理[2]。因此，發展電動公交事業，首先要對其充電基礎設施的規劃建設問題進行研究。

目前，一些學者對電動公交基礎設施規劃問題進行了研究。陳偉等[3]根據充電站內充電樁容量、電動公交車參數計算所需配置充電樁的數量，但沒有考慮公交車充電排隊情況對公交運營的影響。為了討論公交車充電排隊情況，蔡子龍等[4]以充電樁數量最小為目標，在公交樞紐站內建立公交充電排隊系統模型，對直流快速充電模式下高峰和平峰期充電設施最優配置進行了研究。但是該模型并沒有考慮公交運營成本。為了詳細分析運營成本問題，Zou等[5]研究電動公交換電站配置優化問題，以服務可用性為約束、運營成本最小為目標建立模型，優化站內充電樁，并進行了案例分析。Wang等[6]以年總運營成本最小為目標，建立了一個優化電動公交車充電時刻表的模型，模型可以為充電站位置、數量和運營提供相應的決策支持。Li[7]以公交車輛最大行駛里程為約束，建立車輛時刻表模型，分析了電動、燃油、混合動力公交車的總運營成本，并提出了列代算法求解時刻表問題，研究結果表明，電動公交車使用換電形式將不會顯著增加車隊車輛數量。上述文獻側重充電樁配置數量的研究，但同時也有針對充電策略以及政府政策的影響分析。Qin等[8]模擬了佛羅里達州塔拉哈西一天的電動公交運營與充電需求情況，并以減少充電需求為目標，確定了最佳的充電策略。Rick等[9]以量化形式分析了日間停車和免費停車政策對充電行為的影響，并指出在設計政策時應考慮充電行為與政策之間的相互影響關系。

以上文獻，從不同角度基于確定的運營條件優化充電設施配置或充電策略等，但沒有考慮公交線路自身運營條件對充電站及充電樁配置的影響。對于公共交通線路設計與運營優化等問題的研究也有很多。Wirasinghe等[10]確定了以公交運營成本和客運時間成本之和最小化為目標的最優公交服務特性，分析了站間距、接駁巴士區域邊界和車頭時距等運營參數，給出了簡明的最優參數結果。Daganzo等[11]詳細分析了兩點系統、交通走廊系統、二維平面網絡系統在理想與現實情況下的公共交通運營原則與優化方法。Constantin等[12]建立了以乘客乘車時間最小為目標，車輛數量為約束條件的非線性發車頻率優化模型。Ceder[13]將公交調度時刻表編制問題作為一個多目標優化問題，假定乘客到達服從均勻分布，乘客等車時間為發車間隔時間的一半，在此基礎上構建公交發車時刻優化模型。

本文綜合考慮充電站及充電樁配置與公交線路運營特征參數設計兩者的相互影響，在公共交通走廊上，以社會福利最大化為目標建立模型，考慮線路運量約束和車輛充電站內充電等待時間約束，優化站點數量及位置、發車頻率、票價以及線路首末端充電樁數量等。文中還考慮不同的充電策略對充電站內車輛充電排隊等待時間的影響。

1 模型構建

在一條公交走廊上，電動公交車按發車間隔發車，沿公交線路來回循環運行，當電量不足時到首末端充電站內充電，為了確定公交線路最優的站點數量及位置、發車頻率、票價、車隊規模與充電樁數量，構建了如下的優化模型。

1.1 基本假設

為方便建模，進行如下假設：

A1.假設所研究的線性交通走廊長度為B，公交線路總長度等于走廊長度；

A2.電動公交車票價采用單一票價制度；

A3.用線性彈性需求函數來表示乘客對線路服務水平的反應；

A4.乘客選擇最近的公交站點乘車；

A5.公交線路一端發車；

A6.所有電動公交是相同的，電池充電電量與充電時間成正比，電池電量消耗與行駛里程成正比。

1.2 站點乘客需求分析

如圖1所示，在長度為B的線性交通走廊上布設一條電動公交線路，線路上有N個公交站點，Ds表示第s個站點到第一個站點的距離，DN表示線路總長度。用ls表示s站點和s+1站點之間客流分界線，即當乘客位于(s,ls)之間時，表示乘客去s站點乘車，當乘客位于(ls,s+1)之間時，到s+1站點乘車。Ls表示ls到站點1的直線距離。根據A4可知，ls位于s站點和s+1站點正中間，用公式表示為：

(1)

其中，D1=0,LN=DN，在不影響結果的情況下，為了方便下文公式表示令L0=0。

用q(x,s)表示在x處到站點s乘車的乘客數量，根據A3可知：

q(x,s)=g(x)(1-eaus(x)-ewws-eff-evVb)，?x∈[0,B],?s=1,2,…,N，

(2)

其中：g(x)表示在x處人口密度分布；us(x)表示乘客從x處到站點s所用的時間，下文簡稱為訪問時間；ws表示乘客在s站點的平均等待時間；f表示票價；Vb表示公交車最大行駛速度(Vbmax)與實際平均行駛速度(Vb1)之差；ea、ew、ef、ev分別表示us(x)、ws、f以及Vb的彈性系數。

為了保證在x處到站點s乘車的乘客數量大于等于0，應滿足條件

0≤1-eaus(x)-ewws-eff-evVb≤1,?x∈[Ls-1,Ls],s=1,2,…,N。

(3)

根據A4，公式(3)中乘客訪問時間us(x)可以通過乘客所在位置x與s站點之間的距離以及乘客步行速度(Va)計算得到，公式表示為：

(4)

乘客在站點s的等待時間ws計算表達式為：

ws=αH, ?s=1,2,…,N，

(5)

其中：H表示發車時間間隔；α表示系數，可由發車間隔所服從的分布和乘客到達時間間隔分布決定。當公交線路發車間隔和乘客到達時間間隔均服從均勻分布時，α=0.5。

電動公交車的實際平均行駛速度Vb1與站點個數N有關，假設各站點停靠時間固定為β，電動公交在路段上最大行駛速度為Vbmax，則電動公交車的實際行駛速度Vb1可表示為：

(6)

因此，Vb表示為：

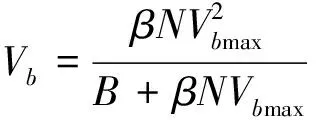
(7)

由此可得各站點乘客數量Qs為：

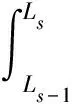
(8)

將公式(2)、(4)、(5)、(7)代入到公式(8)中得到各站點乘客數量Qs為：

(9)

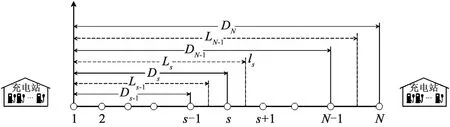
圖1 線性交通走廊上公交線路布局示意圖

1.3 消費者剩余

由于公共交通是公益性的，因此以社會福利最大化作為決策者的目標更為合理。社會福利(W)由消費者剩余(G)和公交運營商純利潤(π)兩部分組成，即：

W=G+π。

(10)

接下來分別對消費者剩余和公交運營商純利潤進行討論。

首先定義站點s的消費者剩余Gs。根據公式(2)可以得到關于票價的需求密度函數為：

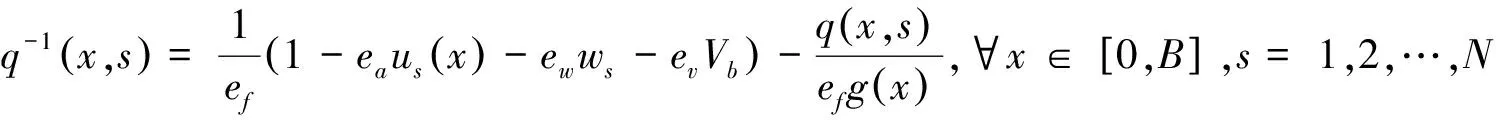
(11)

因此對于乘客從x處到s站點乘車的消費者剩余G(x,s)為：

(12)

所以s站點的消費者剩余Gs為：

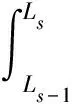
(13)

所以總消費者剩余為：

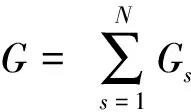
(14)

1.4 運營商純利潤

運營商純利潤(π)等于總收益(R)減去總成本(C)，即：

π=R-C，

(15)

其中，總收益等于各站點乘客票價收益，即：

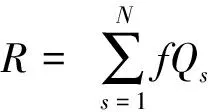
(16)

其中，Qs由公式(8)得到。

運營商的總成本包括購車成本Cb、運營成本Co、充電站及充電樁配置成本Ce、充電等待時間成本Cw4個部分組成，公式表示為：

C=Cb+Co+Ce+Cw。

(17)

購車成本用購買一輛車價格cb乘以車輛總數F，用公式表示為：

Cb=cb·F。

(18)

運營成本僅考慮電動公交車每天車輛運行所消耗的電量成本，根據A6可得：

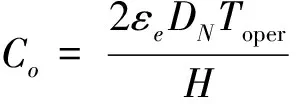
(19)

其中，Toper表示線路每天運行總時間，εe表示單位行駛里程耗電量成本。

充電站和充電樁配置成本包括固定成本與可變成本兩部分，公式表示為：

Ce=Δ0+cΔ，

(20)

其中，Δ0是充電站系統建設固定成本，Δ表示一個充電樁的成本，c表示充電樁總數量。

充電等待時間成本由總充電等待時間乘以單位等待時間成本η。總充電等待時間等于每輛車平均充電等待時間乘以總車輛數。

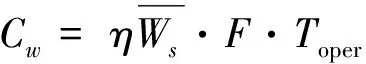
(21)

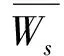
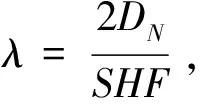
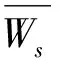
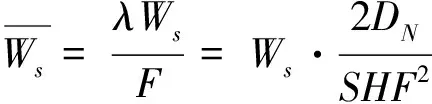
(22)

其中，Ws根據有限源顧客排隊模型(M/M/c/∞/F)得到，具體推導公式如下：

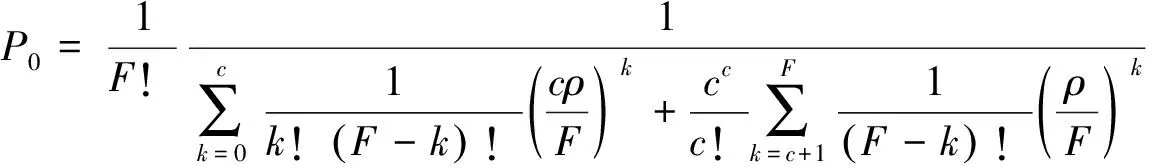
(23)

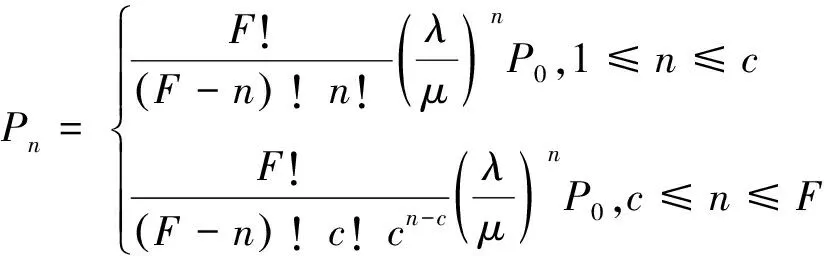
(24)

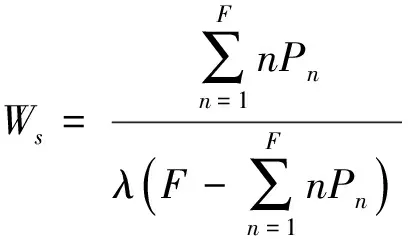
(25)

其中，ρ=λF/cμ，λ表示車輛到達率，μ表示充電樁充電服務速率，F表示車隊總數量，c表示充電樁數量。

由公式(17)～(25)得到運營商每天總成本為：

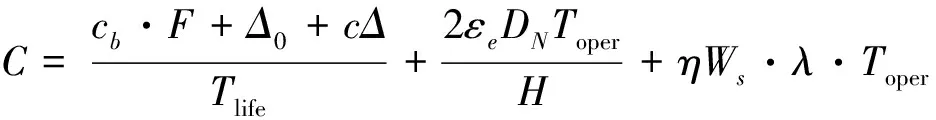
(26)

將公式(14)、(15)、(16)、(26)代入公式(10)得到社會福利為：

(27)

1.5 社會福利最大化模型

根據上文的分析，得出社會福利最大化模型為：

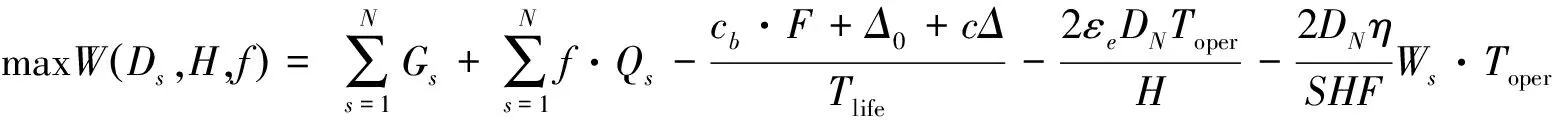
(28)

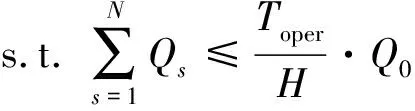
(29)

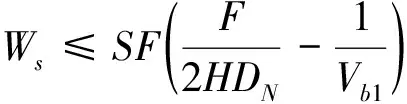
(30)

其中，公式(29)是運量約束條件，表示運量小于運力，其中Q0表示電動公交車的最大裝載量。公式(30)是充電等待時間約束，推導過程如下：

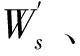
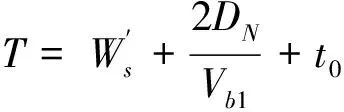
(31)

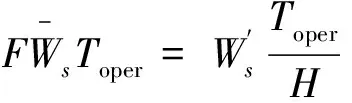
(32)

(33)

由于t0≥0，因此有

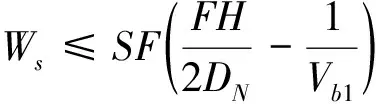
(34)

2 充電策略對比研究

不同城市電動公交車充電策略是不同的，基本可以分為兩種充電方式：(1)公交車持續運營直到電量不足再充電；(2)當車輛一次運行結束后，只要有空閑充電樁則充電。本文基于以上兩種充電策略，對以下兩種情形進行對比分析研究。

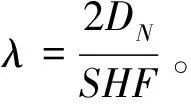
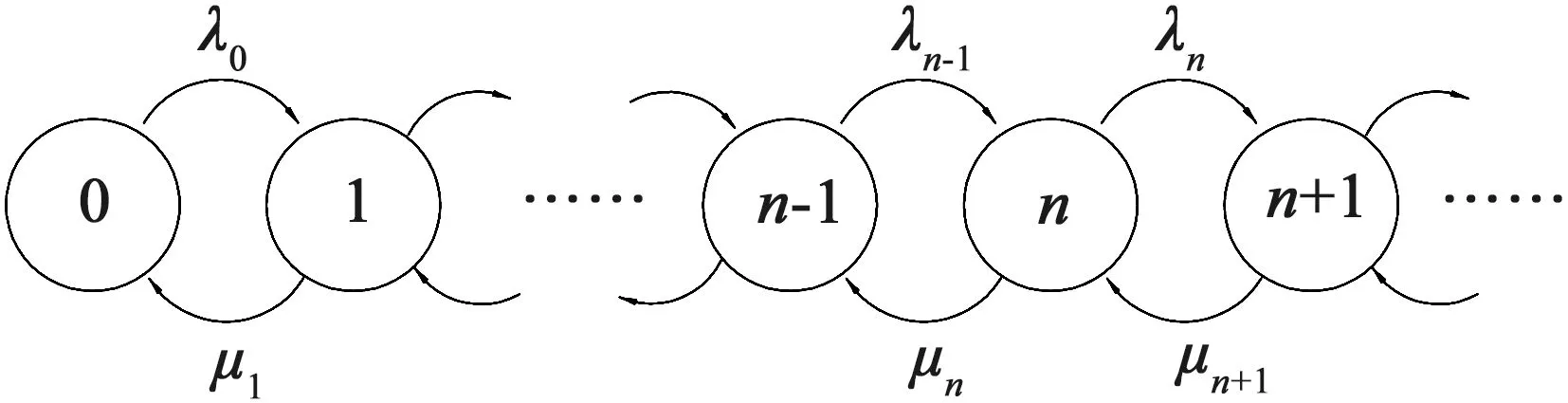
圖2 充電車輛狀態轉移圖

情形二：電動公交車充電規則是當車輛一次運行結束到達充電站時，若有空余充電樁則立即充電，若沒有空余充電樁，則根據車輛剩余電量是否能滿足下一次循環運行來決定是否排隊等待充電。將充電站看成一個排隊系統，系統里面的車輛數用n表示，λn表示系統中有n輛車時的到達率，μn表示系統中有n輛車時的離開率，pn表示系統中有n輛車的平穩狀態概率。圖2為充電站內車輛隊列狀態轉移圖。

在平穩狀態條件下，對于n>0，流入和流出狀態n的期望速率必相等，又有狀態n只能變成狀態(n-1)和(n+1)的事實，因此可得到狀態n的平衡方程為：

λn-1pn-1+μn+1pn+1=(λn+μn)pn。

(35)

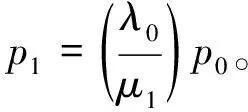
一般地，可用歸納法得到：

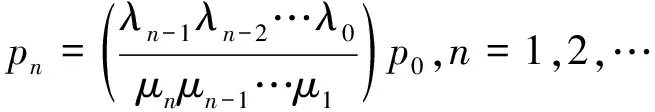
(36)

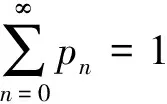
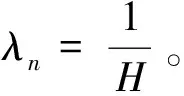
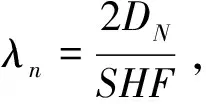
(37)

將公式(37)代入公式(36)即可得到狀態概率pn的值，又有Little公式：

(38)

其中，L系統表示充電站系統中充電車輛的期望數，λeff表示充電車輛有效到達率。因此可以算出充電站內車輛充電等待時間Ws，其中有效到達率計算式為：

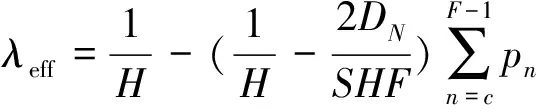
(39)

3 求解算法

根據公式(28)～(30)提出的社會福利最大化模型，以構造拉格朗日函數法設計求解算法，在算例中將本算法與遺傳算法進行對比分析，下面分別介紹拉格朗日函數法求解算法與遺傳算法。

3.1 拉格朗日函數法求解算法

針對所提出的社會福利最大化模型，構造拉格朗日函數，尋求規劃問題的K-T點，運用KKT條件和約束條件建立方程組，并討論乘子的取值以確定最優性條件[14-15]。分別對變量和乘子求偏導，結果如下：

(40)

基于公式(40)設計求解方法，具體步驟如下：

Step2：更新設計變量。根據公式(40)依次更新發車頻率、票價和站間距。

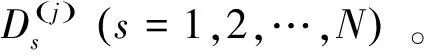
Step4：終止檢查。如果連續迭代得到的目標函數值足夠接近，則終止算法并輸出變量最優解{D*,H*,f*,c*,F*}和最大社會福利值W*。否則，令j=j+1并轉到Step2。

在具體應用中，基于拉格朗日函數法的優化算法流程圖如圖3所示。

值得注意的是，以上的算法步驟是基于確定的站點個數，求解對應站點個數的最優解。由于實際中站點個數是有限的，因此可以通過對比不同站點個數情況下最優社會福利值，得到最終解。

3.2 遺傳算法模型求解

遺傳算法是一種智能算法，一般被用來求解VRP問題，Holland教授在1975年首先提出，是一種基于自然選擇和基因遺傳學的全局搜索方法，通過選擇、交叉、變異等遺傳算子來仿真生物的進化過程，利用適應度函數來表示染色體的優良性。遺傳算法模擬達爾文的自然進化論和遺傳變異理論，適合求解復雜的多極值優化問題和組合問題，具有廣泛的應用價值[16-17]。圖4為遺傳算法流程圖，編碼采用的是二進制Gray編碼，文中社會福利值即作為個體適應度函數。

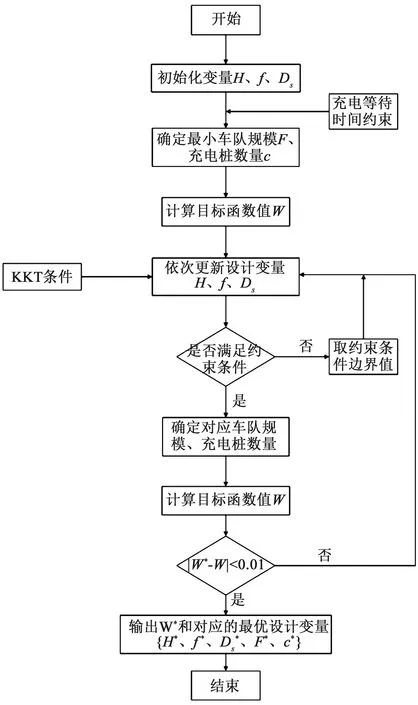
圖3 拉格朗日求解算法流程圖

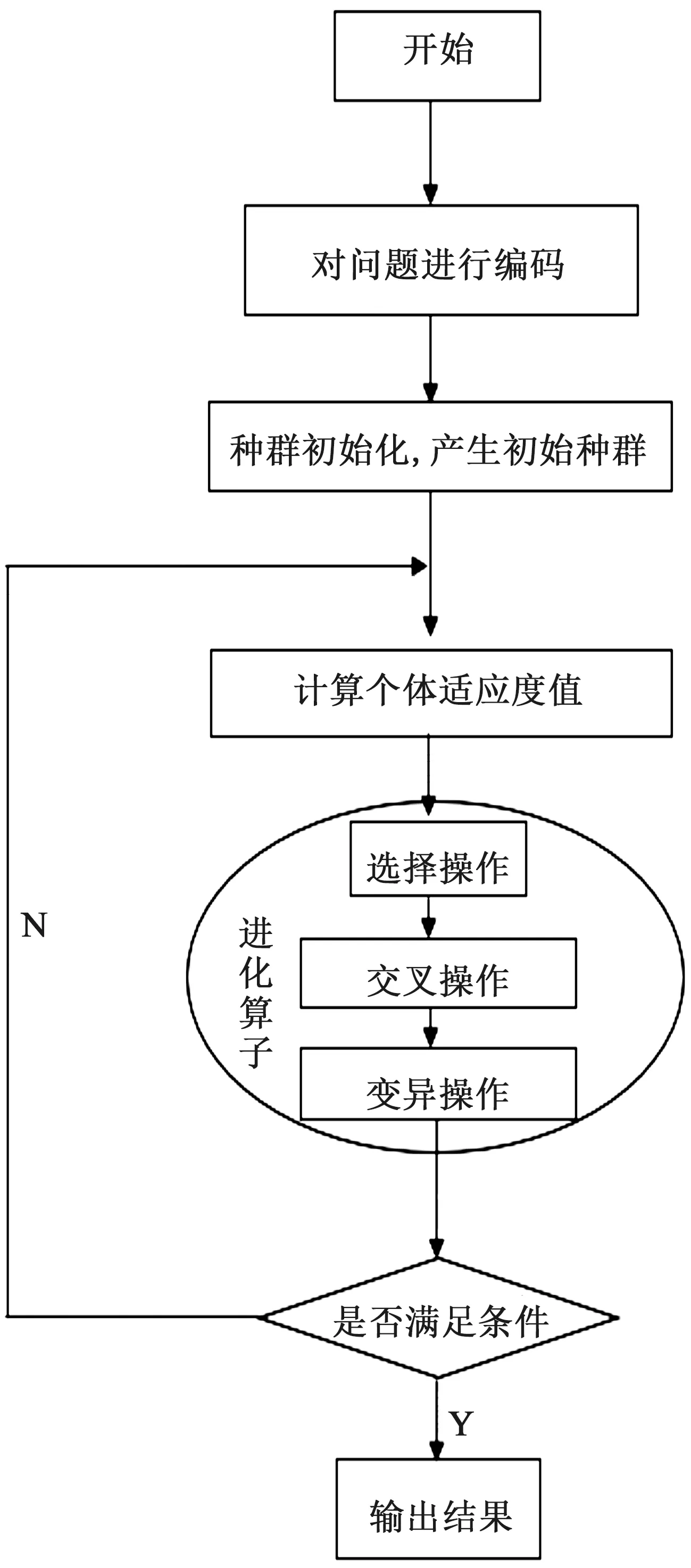
圖4 遺傳算法流程圖

4 算例分析

4.1 算例設置

本節使用一個數值算例來驗證文中所提出的模型和求解算法的有效性。以蘇州市931路純電動公交線路為參考案例，如圖5所示。

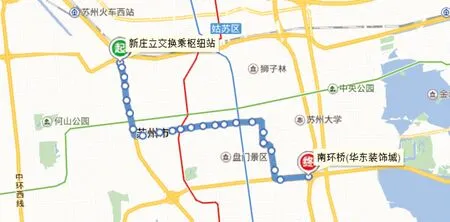
圖5 蘇州市931公交線路圖

蘇州市931路公交車服務于新莊立交換乘樞紐和南環橋站之間，公交線路全長約12.4 km，共有23個站點。算例線路長度B設置為12.4 km，人口密度參考蘇州市區2016年末平均人口密度1184人/km2，其余參數見表1。

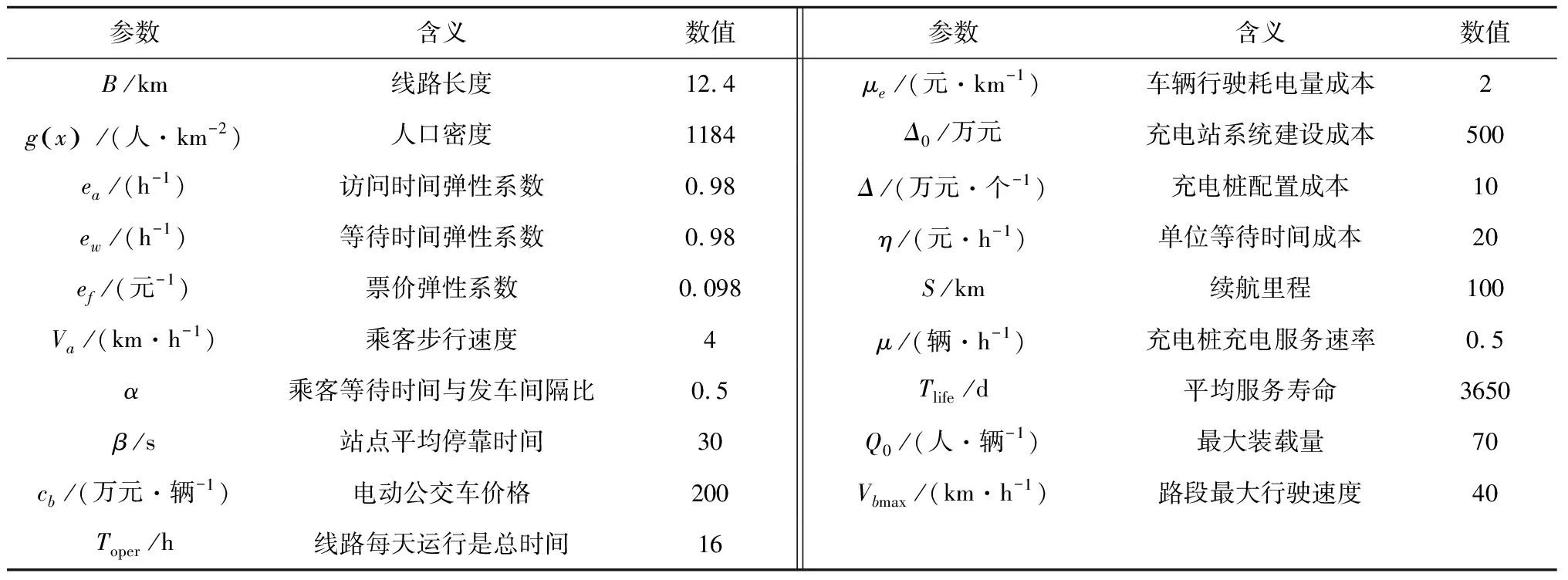
表1 算例參數值

4.2 求解結果分析

4.2.1 基于拉格朗日函數法求解結果

根據第3.1節拉格朗日函數法求解算法對上述算例進行求解。圖6表示在不同站點個數情況下的最優福利值，線條表示圖中點的擬合曲線。圖7表示在不同站點個數情況下，對應求解的最優票價、發車間隔、車隊規模和充電樁數量。從圖6中可以看出，隨著站點的增加，社會福利先增加后減小,其中在第27個站點處社會福利取得最大值，為22 578 元/d。此時票價為0.630 4 元、發車間隔為4.338 9 min、總車隊車輛為27輛、充電樁個數為7個。從圖7中可以看出，隨著站點數增加，車隊規模和充電樁個數逐漸增加，而發車間隔逐漸減小，其中車隊數量增加速度遠大于充電樁數量增加速度。對于票價，根據公式(38)可知其最優值等于運量約束(公式29)的拉格朗日乘子。因此，當最優結果下運力大于運量時，票價則為0，從圖7中也可以看出有很多結果為0的情況，如站點數為14、18、20等時，票價為0。相反，當在社會福利最大化模型中運量約束起作用時，票價則不為0。實際中，應避免票價為0的公交線路設計。原因在于如果票價為0，那么將導致出行者或政府出現機會成本的損失[18]。

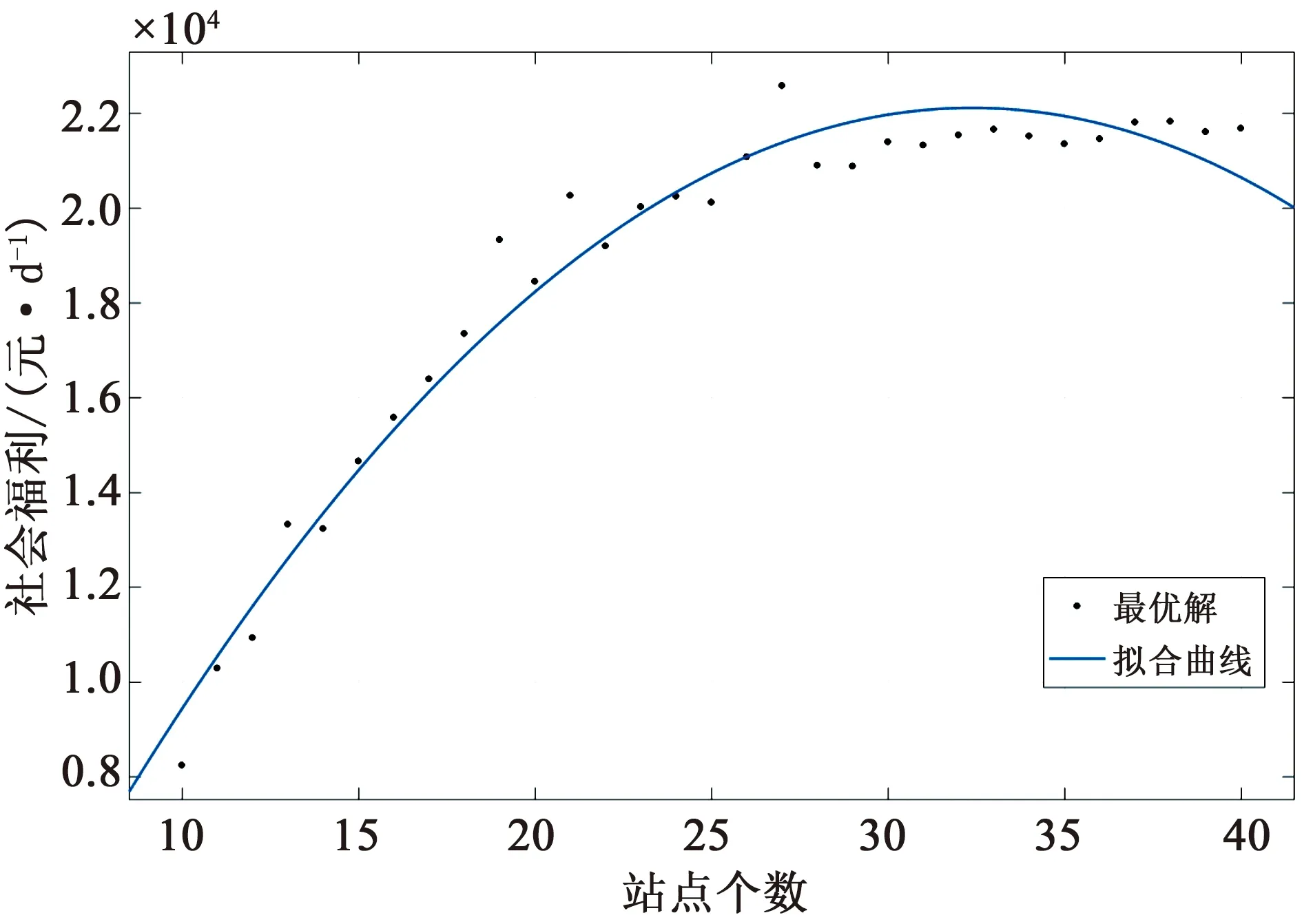
圖6 不同站點個數下的最優社會福利

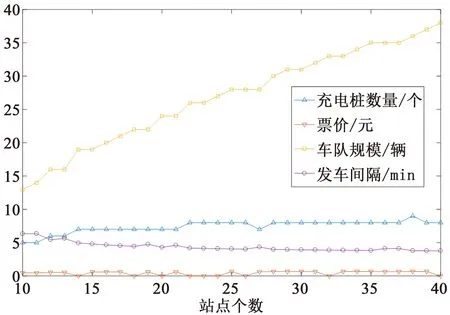
圖7 不同站點個數下各變量最優值

4.2.2 遺傳算法求解結果

用上述算例中同樣的參數，輸入遺傳算法中，求解結果如圖8所示。圖8表示每一代種群適應度變化，其中每一代種群最優適應度值的變化即為解的變化。圖9是圖8中解的變化曲線放大形式，星號點即表示最優解。根據求解結果顯示在第31代得到最優結果值，各變量結果分別為票價0.732 4元、發車間隔為4.278 min、車輛數為29輛、充電樁數量為8、站點個數為31個、社會福利值為22 389 元/d。對比兩種算法求解結果如表2所示

表2 算法求解結果對比

對比結果顯示，拉格朗日函數法求解的最優社會福利值大于遺傳算法求解值，且算法運行效率更高(所使用計算機處理器為i7-8550U，內存8 GB)。

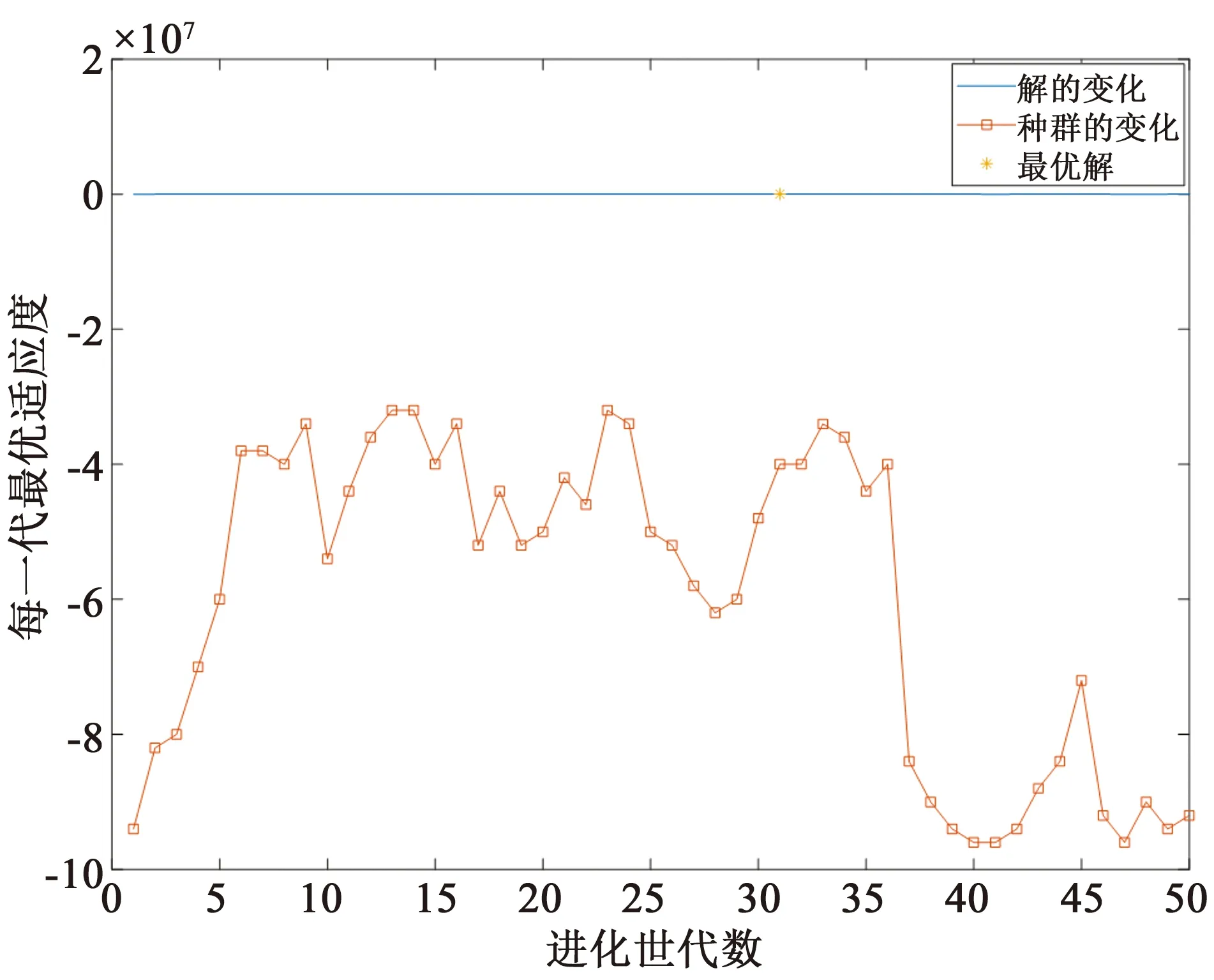
圖8 遺傳算法求解結果圖

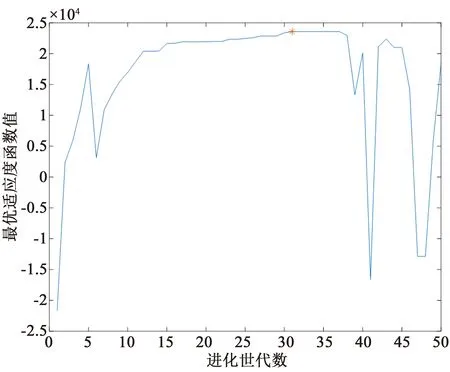
圖9 每一代最優個體適應度值

4.3 充電策略對比研究分析

根據社會福利最大化模型(公式28)可知，在票價、發車間隔、站點位置、車隊規模、充電樁數量不變情況下，社會福利只與車輛充電等待時間成本有關。以上述算例為例，在站點數為27個、票價為0.630 4元、發車間隔為4.338 9 min、總車隊數量為27輛、充電樁個數為7的情況下，根據有限源顧客排隊模型(M/M/7/∞/27)得到Ws=2.224 6。

根據情形二分析，將已知變量代入公式(37)得

因此，根據公式(36)可計算出充電站系統中有n輛車排隊等待的平穩狀態概率pn，表3列出了pn>10-3的值及對應充電系統內車輛數。

表3 主要狀態概率值

根據Little公式計算得到L系統=6.896 6，Ws=3.420 9。對比Ws可得到，在此算例中，情形一優于情形二。

情形一和情形二的優劣只取決于車輛充電等待時間成本，而充電等待時間與發車間隔、線路長度、車隊規模、充電樁數量有關。由于排隊論公式復雜，難以直接化簡比較，因此以數值為例，計算兩種情形下充電等待時間(充電排隊長度)與發車間隔、線路長度、車隊規模、充電樁數量之間的關系。

圖10a、10b分別表示在發車間隔為10 min、充電樁為7個的情況下，情形一和二中車輛充電排隊長度與線路長度和車隊規模之間的關系。從圖10a中可看出，情形一下，線路長度對排隊長度有持續較大影響，而車隊規模對排隊長度有一定的影響，且隨著線路長度變大，影響也變大。而從圖10b顯示，在情形二下，當車輛數F小于等于c+1時，車隊規模對充電樁排隊長度影響很大，這是由于充電樁過多，當車輛數低于充電樁數量時，增加車輛數，即是增加充電車輛總數，因此，總的排隊長度增加，而當車輛數F大于c+1時，車隊規模將對充電樁排隊長度影響變的很小。對于線路長度對排隊長度的影響，從圖10b中可看出，情形二中當線路長度比較短的時候(數值算例中10km以內)，線路長度對排隊長度影響大，而當線路過長時，線路長度對于排隊長度的影響變低。

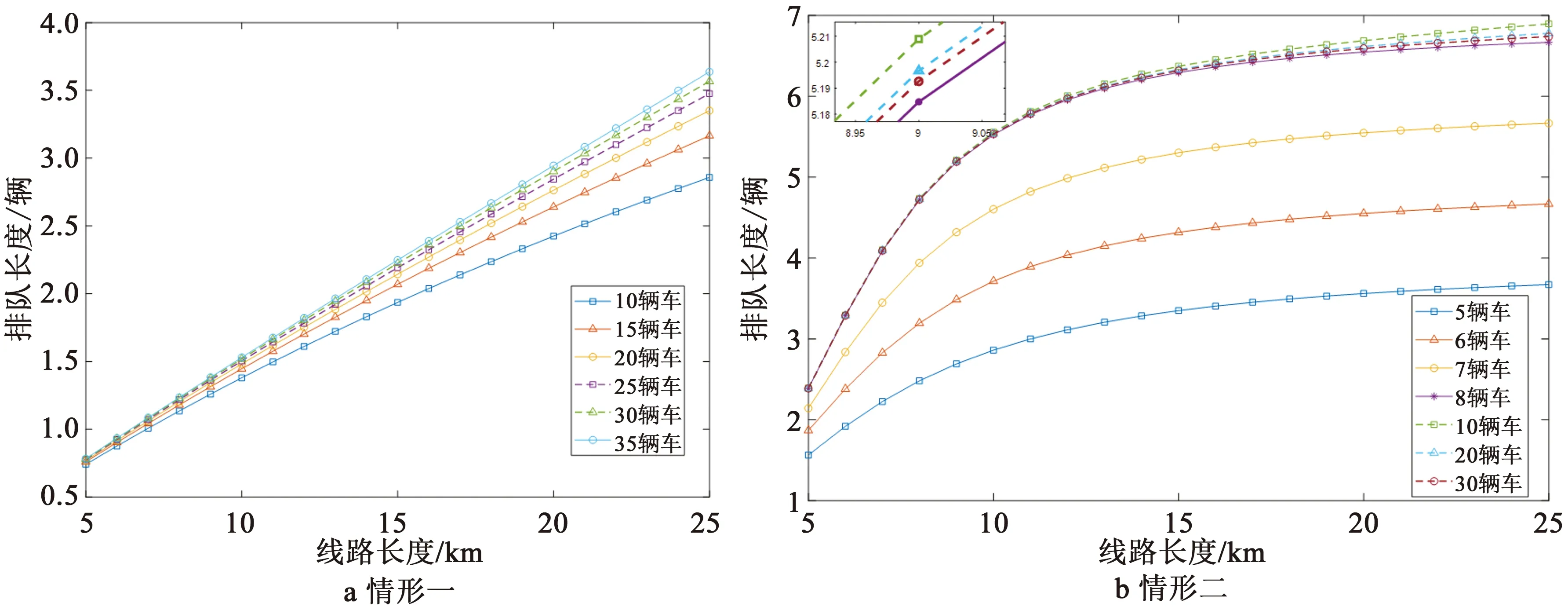
圖10 線路長度、車隊規模和充電排隊長度關系

5 結語

本文以社會福利最大化為目標，建立了線性交通走廊中公交線路設計變量的優化模型。模型考慮電動公交充電等待時間約束，優化了站點數量與位置、發車頻率、票價、車隊規模以及充電樁數量，以拉格朗日函數法求解算法和遺傳算法對模型進行求解，并詳細分析了兩種不同充電策略對充電排隊等待時間的影響，對不同條件下充電策略的優劣進行了比較分析。該模型可為電動公交車線路規劃提供決策依據。

依托本文的優化模型，可進一步從以下幾個方面進行拓展：(1)往往有多條線路共用一個首末站，因此未來可以進一步研究這個因素對充電樁配置的影響以及電動公交線網規劃問題。(2)本文沒有考慮人口密度大小對線路參數設計的影響，不同城市人口密度相差很大，而且同一地區隨著時間的推移人口密度也會產生較大變化，因此，分析人口密度的影響具有現實意義。(3)車輛規模化生產、充電電池技術進步以及政府補貼政策變化對車輛價格的影響以及車輛運行速度對模型的影響有待進一步研究。