Shimizu-Morioka系統與Finance系統生成Lorenz混沌的微分幾何策略*

張端 施佳琴 孫瑩 楊旭華 葉蕾

1) (浙江工業大學計算機科學與技術學院, 杭州 310023)

2) (浙江理工大學建筑工程學院, 杭州 310018)

從一種受控混沌系統生成另一混沌系統可增強保密通信的安全性, 具備潛在應用前景.研究了如何通過狀態變換以及單輸入反饋, 驅使受控Shimizu-Morioka系統與受控Finance系統生成Lorenz混沌動態.主要方法是運用微分幾何理論, 將上述三種系統等價轉換為下三角形式, 并盡量簡化和一致化其方程形式, 使得上述三種不同的3階系統的前兩個方程形式相同, 然后對受控Shimizu-Morioka系統與受控Finance系統設計單輸入反饋控制第三個方程的形式, 以便達到生成Lorenz混沌的目的.運用該方法, 設計了受控Shimizu-Morioka系統通過狀態變換和單輸入狀態反饋, 混沌反控制生成Lorenz混沌的控制策略; 也設計了受控Finance系統通過狀態變換和單輸入狀態反饋, 廣義同步到Lorenz混沌的控制策略.最后, 借助數值仿真驗證了上述混沌反控制和廣義同步的有效性.

1 引 言

近五十年來, 混沌理論研究迅速興起, 并在保密通信、物理、生物醫學、化工、經濟金融、圖像、神經網絡等領域出現眾多成功應用的案例[1-5].以保密通信為例, 其功能的實現依賴于通信系統發送端以及接收端可生成一致的混沌信號, 若能生成可變的混沌信號, 必將提高其保密能力[3].為此, 本文關注從一種動態系統精確或者近似生成另一特定混沌動態的問題.

混沌反控制和廣義同步均屬生成混沌的方法.混沌反控制通常指受控系統經狀態變換和狀態反饋等價轉換為某混沌系統[6-8].廣義同步的一種定義為受控系統從任何初值開始的軌跡, 經過狀態變換以及可調整的狀態反饋輸入, 漸進跟蹤某混沌系統從任何初值開始的軌跡, 或者該軌跡經某狀態變換后得到的新軌跡[9-13].可見二者在方法上存在頗多共性, 只是廣義同步考慮了初值不匹配的問題,因此我們綜合討論兩種方法的相關文獻.近年來,混沌反控制和廣義同步的研究取得了一系列精彩的成果, 大致上可分為三類.第一類, 為了簡化狀態變換的構建, 通常選取線性變換, 并采用多輸入狀態反饋以生成給定的混沌動態[6,14-16].第二類方法的策略是為混沌系統加入合適控制量, 若經運用非線性控制理論中的反饋線性化方法可以將其轉換為線性能控系統, 那么采用其逆過程, 線性能控系統通過狀態變換和狀態反饋將生成該混沌系統,該方法所得狀態變換一般為非線性的[17-19].第三種方法不考慮狀態變換, 僅施加適當的反饋, 調節系統的李亞普諾夫指數, 從而生成混沌動態[20-22].

基于保密通信等領域的應用前景, 試圖利用受控Shimizu-Morioka混沌系統[23]和受控Finance混沌系統[24]生成Lorenz混沌[25].相較上述第一類和第三類文獻, 本文將構造非線性狀態變換和單輸入反饋實現上述兩系統生成Lorenz混沌, 目前未見類似報道.囿于Lorenz系統的特點, 也無法采用第二類文獻中的反饋線性化方法, 故轉而尋求轉換系統為下三角形式, 并設計一種新型轉換方式以盡可能簡化其下三角形式.主要策略為運用微分幾何方法, 對三種系統方程做下三角化, 并盡量簡化和一致化其形式, 最終此三種不同3階系統各具有兩個同形式的方程, 兩受控系統的余下一個方程由單輸入反饋調整其形式, 從而生成Lorenz系統.首先考慮Lorenz系統是否可能轉換為下三角形式, 為Lorenz混沌系統配置了一個帶參數的線性輸入向量場形成受控系統, 反復操作李導數證明該受控Lorenz系統可等價轉換為下三角系統, 因此Lorenz混沌系統本身也可轉換為下三角形式.其次, 利用多向量場三角化的方法, 避免了求解偏微分方程組, 構造非線性狀態變換, 求得等價于Lorenz混沌系統的下三角系統.進一步, 通過局部狀態變換和參數選擇等方法簡化與Lorenz系統等價的下三角形式.然后, 對受控 Shimizu-Morioka混沌系統以及受控Finance混沌系統做類似的下三角化處理, 結論是此三個3階動態系統各自下三角形式的前兩個方程一致, 表明三種不同混沌內在具有一定的相似性.最后, 利用上述相似性, 實現了受控Shimizu-Morioka系統生成Lorenz混沌,以及受控Finance系統與Lorenz混沌的廣義同步.本文討論的異構混沌系統生成Lorenz混沌的技術在保密通信系統中可能會有兩種潛在應用.一種在通信系統發送端應用混沌反控制技術, 使其能夠生成兩種甚至多種混沌信號, 提高靈活性.另一種,發送端利用電路實現Lorenz系統并調制信號, 而在接收端則實現受控Shimizu-Morioka系統或者受控Finance系統, 并應用廣義同步技術解調信號, 由于發送端和接收端異構, 當其中一端失密時,另一端仍具備一定保密性, 較自同步技術更為安全, 具體調制解調方法可參見文獻[3].

本文余下部分安排如下：第2節給出本文討論主要問題的數學描述; 第3節在一定范圍內討論了Lorenz系統等價轉換為下三角形式的各種可能, 并選擇了其中的最簡形式; 第4節設計并仿真了單輸入受控Shimizu-Morioka系統通過狀態變換和反饋混沌反控制生成Lorenz混沌, 以及單輸入受控Finance系統與Lorenz混沌的廣義同步;第5節總結全文.

2 問題描述

Lorenz系統是經典混沌系統, 具體形式為[25]

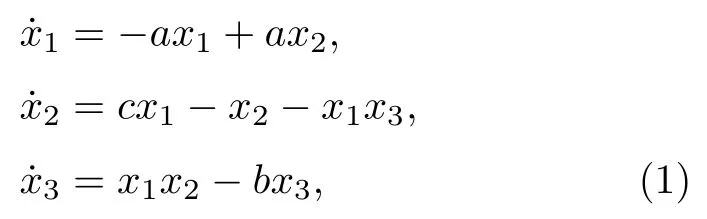
其中x=(x1,x2,x3)T是狀態變量;a,b和c是已知的正實參數, 選取適當參數時系統具有混沌特性,本文要求 2a-b=0 .為該系統增加線性控制向量場成為單輸入受控Lorenz系統

其中v為標量輸入;k1,k2和k3均為實數并且不全為0.由于系統(2)無法在全局等價轉換為線性能控系統(第3節說明原因), 將考察其能否等價轉換為下三角形式的非線性仿射系統[26]

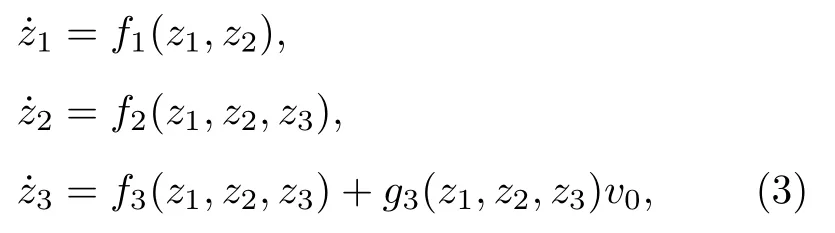
其中z=(z1,z2,z3)T是狀態變量;v0為標量輸入;f1,f2,f3和g3均為光滑函數.轉換系統 (2), 使其符合下三角形式(3)的一種直接的方法是取z1=x1,z2=x2,z3=x3,k1=k2=0 和k3=0 ,但無益于簡化系統(2)也無明顯實用性.設置參數k1,k2和k3的主要目的是搜尋一種形式簡單, 并且等價于系統(2)的下三角系統.尤其考慮系統(2)是否可能等價轉換為如下特殊的下三角形式, 也是一種特殊的部分線性化形式[26,27]

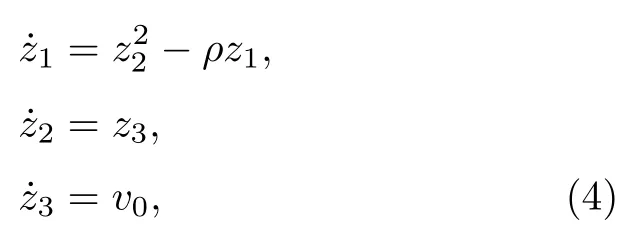
這里ρ為實數,v0為標量輸入, 因為兩種重要的受控混沌系統, 受控Shimizu-Morioka系統和受控Finance系統, 均可經簡單處理(下文給出)等價轉換為此形式.如果系統(2)也可等價轉換為系統(4), 意味著此二受控系統可生成Lorenz混沌, 實現混沌系統的轉換.

所謂系統(2)等價轉換為系統(3)或系統(4),是指系統 (2) 選取合適參數k1,k2和k3, 再經光滑狀態變換

以及單輸入狀態反饋

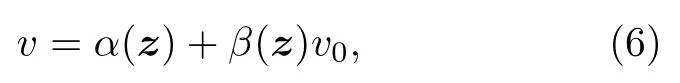
其中α(z) 和β(z) 為光滑函數, 轉換為系統(3)或系統(4).上述定義表明等價轉換具有對稱性, 因此若系統(2)能等價轉換為系統(4), 則系統(4)也可等價轉換為系統(2), 進而取v為0得到系統, 即生成了Lorenz混沌.

3 等價轉換

本節工作按如下兩步驟進行：第一, 討論系統(2)等價轉換為下三角系統(3)的可行性; 第二, 構造狀態變換和反饋實現等價轉換, 并在此過程中調整參數, 最終轉換為系統(4).

3.1 等價轉換的可行性

記系統(2)的漂移向量場為

以及輸入向量場為

設X和Y為光滑向量場, a dXY=[X,Y] 為此二向量場的李導數[28].令X0=G,X1=adX0F,X2=adX1F, 系統(2)能等價轉換為下三角系統(3)的充要條件是此三向量場張成的分布span{X0,X1,X2}在原點的某個鄰域內幾乎處處(除一個零測度集外)滿秩并且 s pan{X0,X1} 在原點的某個鄰域內幾乎處處 (除一個零測度集外)對合[26].如果span{X0,X1}在原點的某個鄰域內正則對合, 則可以轉換為部分線性化形式[26,27], 但是否可等價轉換為系統(4), 仍需在轉換實現過程中進一步考察.本小節依據上述條件檢驗受控Lorenz系統(2)并做參數分析.

計算如下向量場李導數

考察X0與X1的對合特性,

對合條件要求

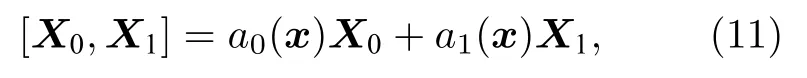
其中a0(x) 和a1(x) 為光滑函數.注意到僅當如下等式滿足時(11)式才在全局成立,

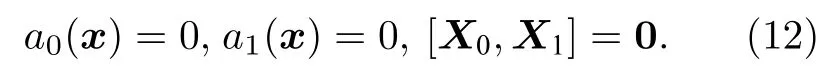
如此限制了k1,k2和k3的選擇, 只有兩種可能：一種可能為

另一種可能為

第一種可能中排除了k1=0 并且k2=0 的情況, 否則當x1=0時 sp an{X0,X1} 秩為1, 說明在原點的任何鄰域內不可能實現部分反饋線性化[27,28], 更不可能反饋等價轉換為系統(4).

考察第一種可能, 此時

依據反饋線性化的要求, 進一步計算李導數

由X0,X1和X2構成的如下行列式

可知x狀態空間中存在曲面滿足Det(X0,X1,X2)=0, 這是由于向量場X2存在奇異性, 造成無法實現全局范圍的狀態反饋線性化.

由于 sp an{X0,X1} 滿秩并對合,span{X0,X1,X2}幾乎處處(除零測度集即曲面Det(X0,X1,X2)=0以外)滿秩, 確保了系統(2)可等價轉換為系統(3).

對于(14)式表示的第二種可能, 做類似分析計算(過程略), 在原點的任何鄰域中都無法等價轉換為系統(4)的形式, 故不做進一步討論.

3.2 等價轉換的實現

至此, 仍需討論系統(2)如何轉換為系統(3),以及是否可轉換為系統(4).在已計算X0,X1和X2的前提下, 為獲取狀態變換h(x)=(h1(x),h2(x),h3(x))以實現等價轉換, 通常是需要解偏微分方程組0 以及偏微分方程組0[26,27], 以選取h1(x) 和h2(x) , 并另選任一與此二者獨立的函數h3(x) 組成完整的狀態變換, dh1(x) ,dh2(x)和 dh3(x) 均為光滑的正則 1-形式[28], 盡管Frobenius定理保證了方程組的可解性[28], 但是較為遺憾的是求解頗為不易, 采用Maple 18和Mathematica 11兩種符號計算工具求解上述偏微分方程組均沒有成功.因此, 就本系統而言, 上述方法理論上可行, 實際較難達成.本小節將利用微分幾何技巧, 交替推進狀態變換和正交化, 避免了求解偏微分方程組, 實現系統下三角化.

在該變換ψ誘導的切映射ψ?作用下[28],

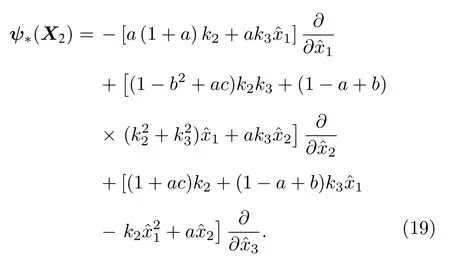
按如下方式定義一組向量場

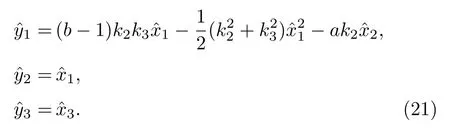
在該變換φ誘導的切映射φ?作用下,

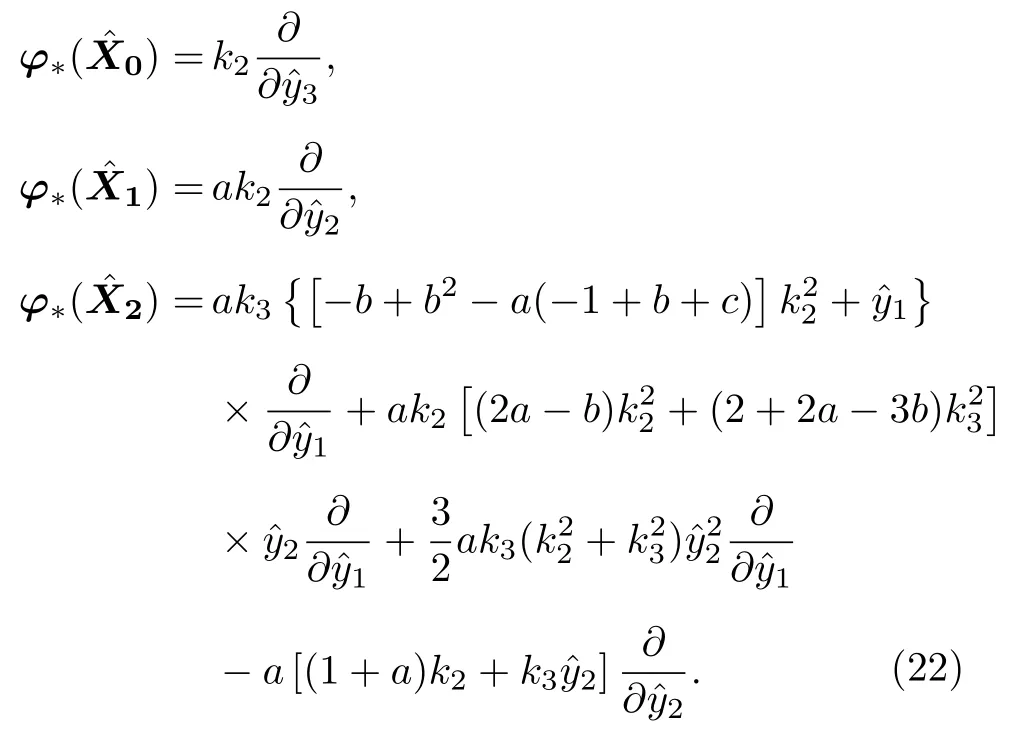
根據 (19), (20)和 (22)式,

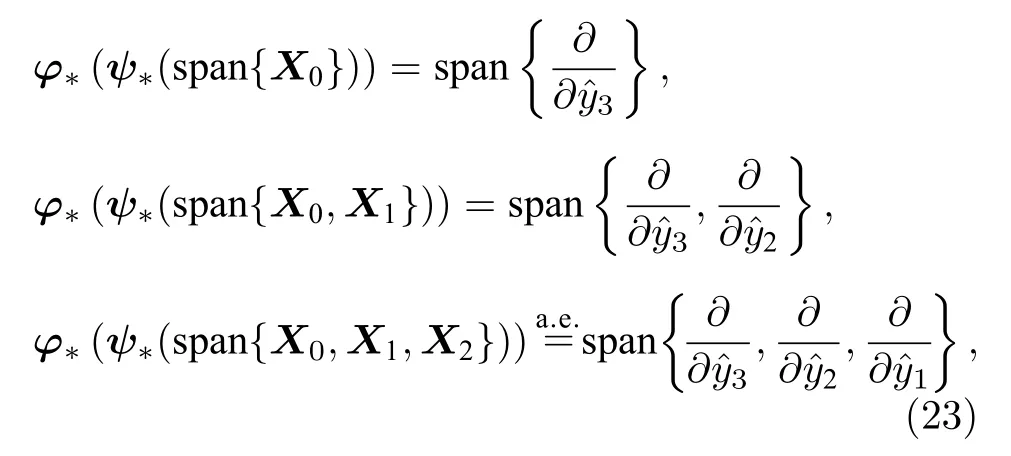
其中第三個式子表示左邊幾乎處處等于右邊, 只有一個零測度集除外, 因為左邊的分布不是處處正則的.(23)式表明利用坐標y寫出的系統必有下三角形式[26],

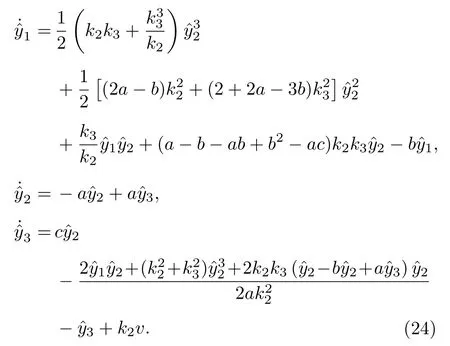
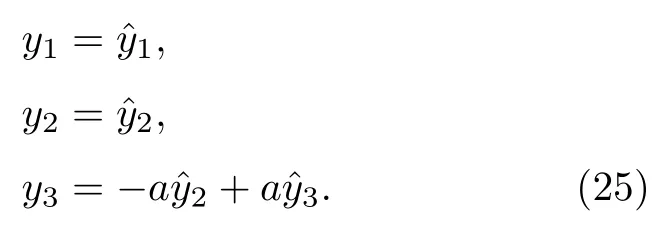
該坐標下的系統方程為

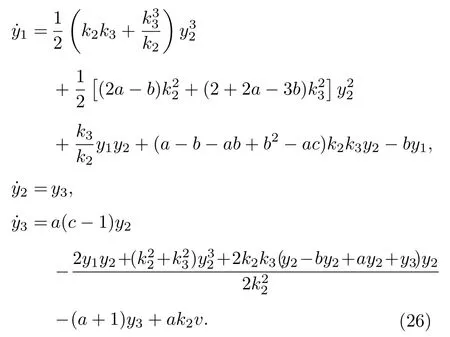
此形式的第一和第三個方程仍相當繁復, 引入標量輸入v為

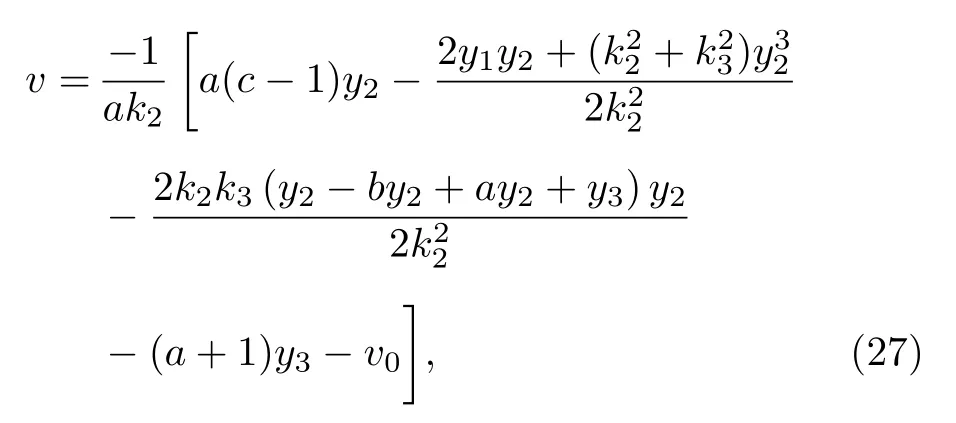
同時選取k3=0 , 系統 (26) 簡化為

為符合系統(4)的形式要求, 再取狀態變換z=(z1,z2,z3)T=ω(y),

系統成為

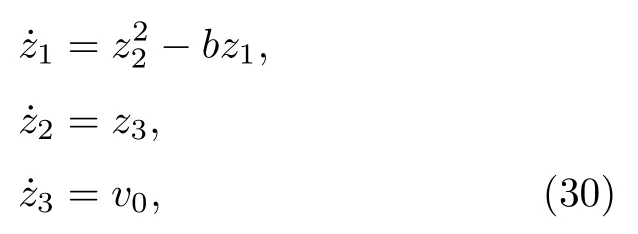
滿足了系統(4)的形式.可驗證至此所作的狀態變換均為微分同胚變換, 綜合上述變換以及k3=0 ,由原始狀態x表示的狀態變換z=T(x) 如下：

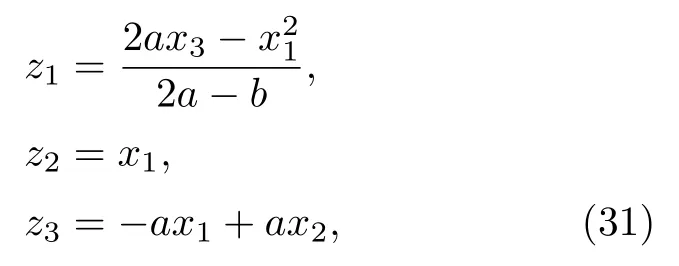
逆變換x=T-1(z) 為

Lorenz系統(1)在狀態z下表示為

4 單輸入非線性系統生成Lorenz混沌

Shimizu-Morioka系統是Shimizu和Morioka于1980年提出的著名混沌系統[23], Finance系統則是反映了金融政策與經濟增長之間關系的混沌系統.本節對受控Shimizu-Morioka系統和Finance系統, 設計狀態變換和單輸入反饋, 分別實現混沌反控制生成Lorenz混沌和廣義同步到Lorenz混沌.

4.1 Shimizu-Morioka系統生成Lorenz混沌

受控Shimizu-Morioka系統的形式如下[23]：

其中ζ=(ζ1,ζ2,ζ3)T是系統狀態,α和β為參數, 要求β與系統中的b相等, 即β=b,u是標量輸入.

系統(34)做線性狀態變換θ=(θ1,θ2,θ3)T=τ(ζ),

以θ為狀態, 系統方程表示為

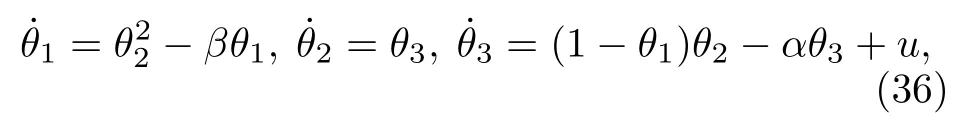
再做狀態反饋

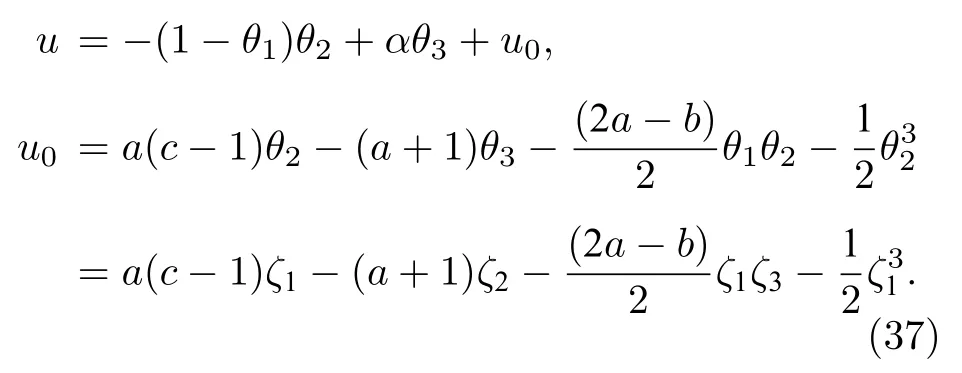
同時考慮到β=b, 系統方程成為

該系統與經狀態變換z=T(x) 的Lorenz系統(33)具有相同形式.所以, 對受控 Shimizu-Morioka系統(34), 利用反饋(37)和狀態變換T-1(τ(ζ)) 將生成Lorenz混沌.

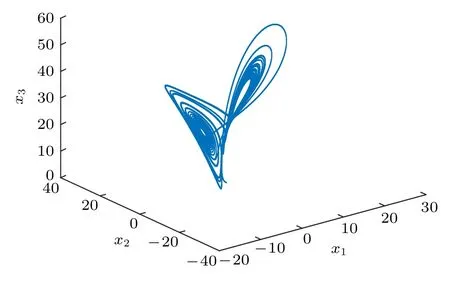
圖1 Lorenz 系統軌跡Fig.1.Trajectory of the Lorenz system.

圖1給出了Lorenz系統(1)的軌跡, 參數為a=10,b=8/3 ,c=30 , 初 值 選 取x1(t0) = 2,x2(t0) = 2,x3(t0) = 2.圖2 給出了受控 Shimizu-Morioka系統(34)在反饋(37)作用下的軌跡, 參數為α=0.75 ,β=8/3 , 初值由 Lorenz系統的初值計算得到, 即ζ(t0)=τ-1(T(x(t0))) , 實 際 上ζ1(t0)=2,ζ2(t0)=0 ,ζ3(t0)=2.076923076923 .圖3為受控Shimizu-Morioka系統標量輸入u的曲線.圖4對圖2所示受控Shimizu-Morioka系統軌跡做了狀態變換T-1(τ(ζ)) , 生成的軌跡與圖1一致,表明混沌反控制生成了Lorenz混沌.

圖2 受控 Shimizu-Morioka 系統軌跡Fig.2.Trajectory of the controlled Shimizu-Morioka system.

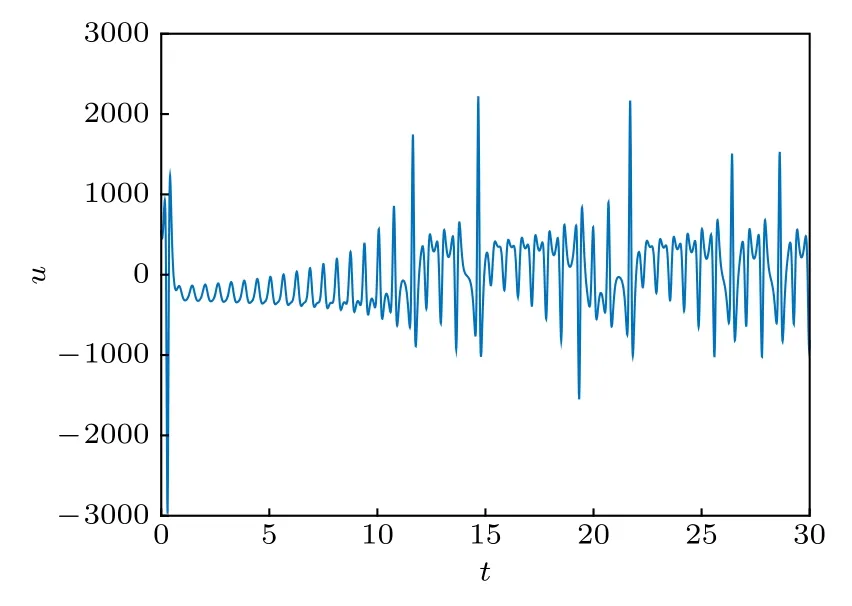
圖3 受控 Shimizu-Morioka 系統的標量控制輸入Fig.3.Scale control input for the controlled Shimizu-Morioka system.

圖4 經狀態變換 T -1(τ(ζ)) 受控 Shimizu-Morioka 系統軌跡Fig.4.Trajectory of the controlled Shimizu-Morioka system via the state transformation T -1(τ(ζ)) .

4.2 Finance系統生成Lorenz混沌

Finance系統具有可相互等價轉換的兩種系統方程形式, 本文選取的形式如下[24]：

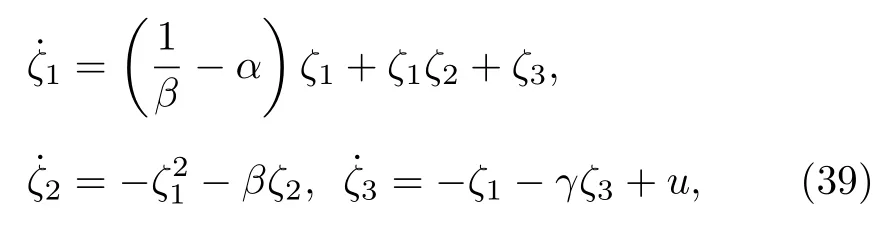
其中ζ=(ζ1,ζ2,ζ3)T是狀態變量;α,β和γ為參數,要求β與系統中的b等值;u是標量輸入.

受控Finance系統到Lorenz混沌的廣義同步定義為：設Lorenz系統(1)與系統(39)在初始時刻t0狀態分別為x(t0) 和ζ(t0) , 對系統(39)施加狀態反饋

其中t為時間,ζ和x狀態分別做變換

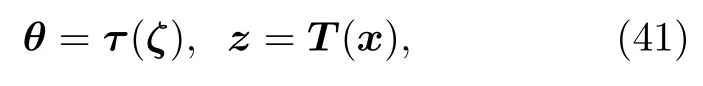
使得系統(39)與系統(1)的軌跡, 按下式的意義漸進地趨于一致

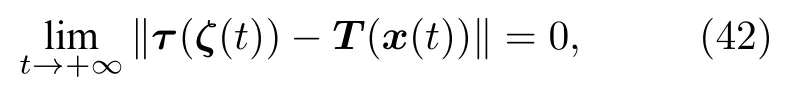
這里 ||·|| 表示了歐氏空間中向量的2-范數.

受控Finance系統做狀態變換θ=(θ1,θ2,θ3)T=τ(ζ),

對應的逆變換為ζ=τ-1(θ) , 即

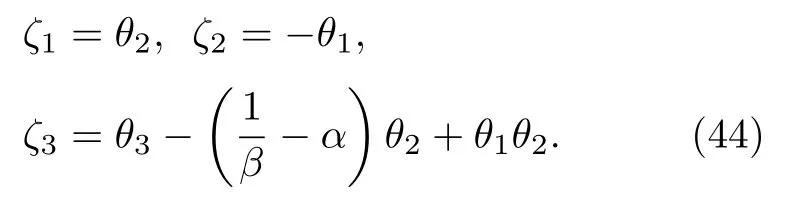
θ狀態下系統方程組為

設計反饋

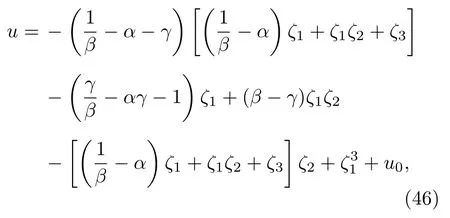
由于β=b, 系統成為

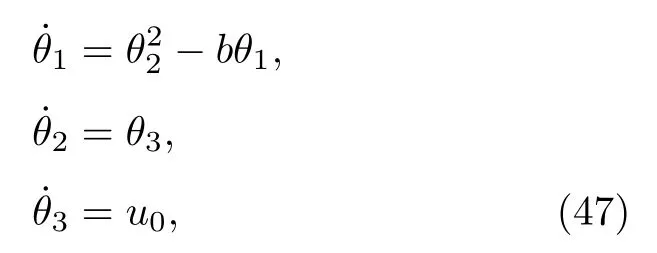
符合系統(4)的形式要求.

考慮同步系統(47)與系統(33), 設兩系統的狀態誤差為ε=θ-z=(ε1,ε2,ε3)T,ε動態為

做如下狀態反饋

此時ε動態為

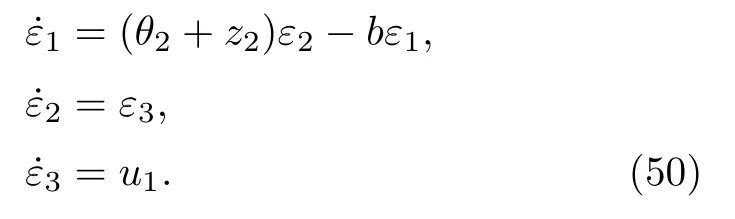
若取該系統的第二和第三個方程組成子系統

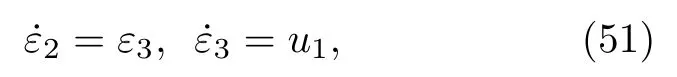
若在 有限時間后, 比如當時間t＞t1時鎮定到ε2(t)=ε3(t)=0, 則在t＞t1時系統(50)的第一個式子簡化為=-bε1, 對于b＞0 的情況該式漸近穩定, 從而系統 (50)漸近穩定, (42)式滿足, 受控Finance系統到Lorenz混沌系統的廣義同步可實現.

對系統(51)滿足有限時間鎮定的經典控制器為[29]

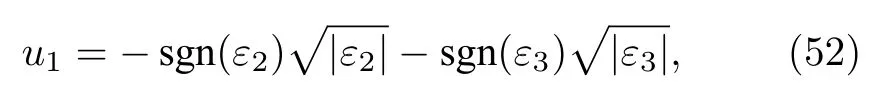
這里 s gn(·) 為符號函數.利用該控制器, 做廣義同步仿真.Lorenz系統參數和初值選取同前, 軌跡已見于圖1.圖5給出了受控Finance系統的軌跡,參數α=0.001 ,β=8/3 和γ=1.1 , 初 值ζ1(t0)=0.2,ζ2(t0)=-3.6 ,ζ3(t0)=0.2 , 與 Lorenz系 統存在初值不匹配, 經計算誤差系統初值ε1(t0)=1.523076923076923,ε2(t0)=-1.8 ,ε3(t0)= —0.4452圖6為Finance系統的標量輸入u的曲線.圖7對圖5所示受控Finance系統軌跡做狀態變換T-1(τ(ζ)), 生成的軌跡同步于圖1, 這被圖8中的軌跡進一步驗證, 該軌跡反映了圖1與圖7軌跡的誤差δ, 其各分量均趨于 0, 圖8 曲線不甚光滑, 其原因是控制器(52)非光滑.仿真驗證了廣義同步的實現.

圖5 受控 Finance 系統軌跡Fig.5.Trajectory of the controlled Finance system.

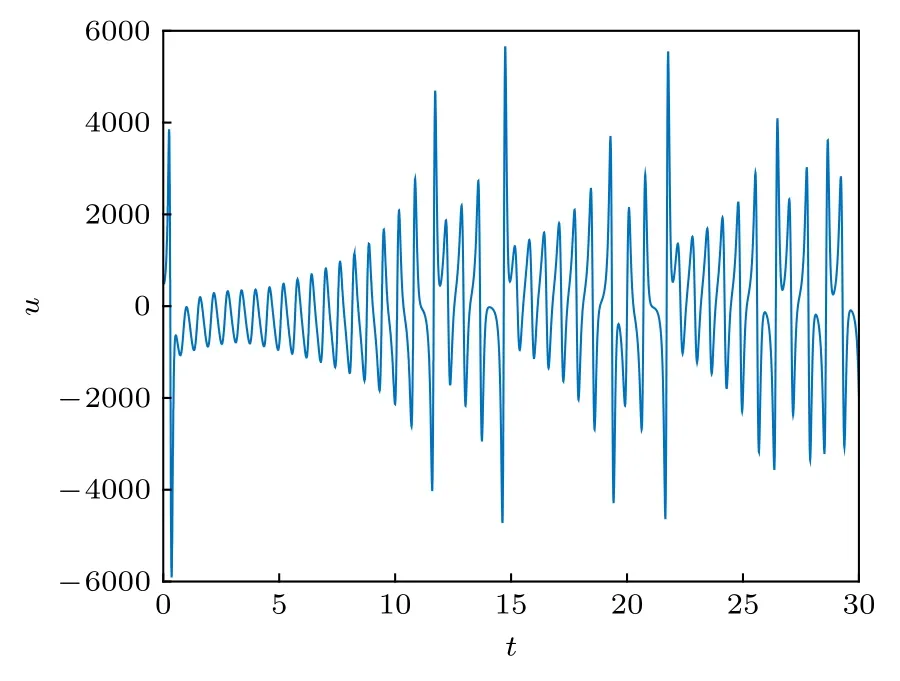
圖6 受控 Finance 系統的標量控制輸入Fig.6.Scale control input for the controlled Finance system.

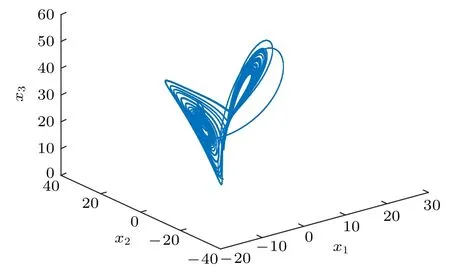
圖7 經狀態變換 T -1(τ(ζ)) 受控 Finance 系統軌跡Fig.7.Trajectory of the controlled Shimizu-Morioka system via the state transformation T -1(τ(ζ)) .

圖8 Lorenz 系統軌跡與經狀態變換 T -1(τ(ζ)) 的受控Finance系統的誤差Fig.8.Error between the trajectory of the Lorenz system and that of the controlled Finance system via the state transformation T -1(τ(ζ)) .

5 結 論

本文研究了如何從受控Shimizu-Morioka系統和Finance系統生成Lorenz混沌的問題, 在方法和結果上總結創新之處如下.

1)利用微分幾何控制理論以及參數優選, 將Lorenz混沌系統等價轉換為某種下三角形式, 使得該三階系統中前兩個方程形式較原Lorenz系統簡化.

2)將單輸入受控Shimizu-Morioka混沌系統以及受控Finance混沌系統等價轉換為下三角形式的仿射非線性系統, 其前兩個方程均與轉換后的Lorenz系統的前兩個方程一致, 揭示了三種不同混沌系統內在具有一定程度的相似性.

3)利用上述相似性, 采用單輸入實現了兩種異構受控混沌系統生成Lorenz混沌, 即單輸入受控Shimizu-Morioka系統混沌反控制到Lorenz混沌以及單輸入受控Finance系統到Lorenz混沌的廣義同步.

此外, 單輸入受控Lorenz系統混沌反控制或者廣義同步到Shimizu-Morioka混沌以及Finance混沌等問題雖未涉及, 利用本文給出的策略均可方便地實現.